大家好!今天继续更新LeetCode热题100系列,第五题我们来学习中等题"盛最多水的容器"。这道题是双指针技巧的经典应用,核心考查如何通过贪心策略优化遍历过程。接下来,我们从题目分析、思路推导到Java代码实现,逐步掌握最优解法。
一、题目描述
首先明确题目要求(基于LeetCode官方原题):
- 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
- 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
- 返回容器可以储存的最大水量。
- 说明:你不能倾斜容器。
示例
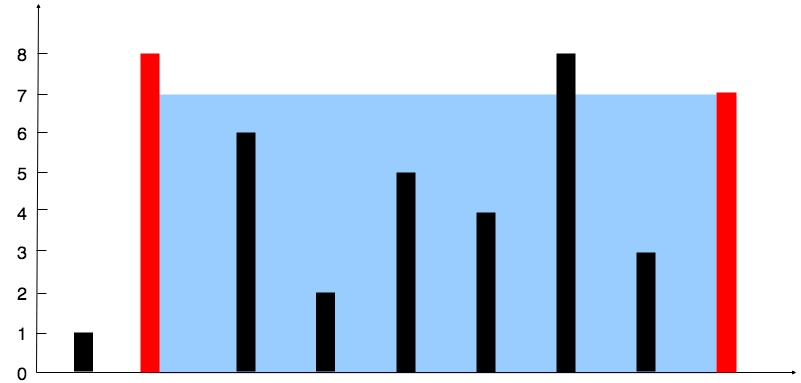
示例1: 输入:height = [1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例2: 输入:height = [1,1]
输出:1
提示
- n == height.length
- 2 <= n <= 10⁵
- 0 <= height[i] <= 10⁴
二、解题思路分析
这道题的核心是计算"两条垂线与x轴构成的容器的盛水量",并找到最大值。盛水量的计算公式是:min(左垂线高度, 右垂线高度) × 两条垂线之间的距离。
1. 暴力解法(时间不达标)
思路
遍历所有可能的两条垂线组合,计算每个组合的盛水量,记录最大值。
问题
时间复杂度为O(n²),当n=10⁵时,运算次数达10¹⁰,会超时,因此必须优化。
2. 最优思路:双指针法(O(n)时间)
核心逻辑
利用"贪心策略",通过左右指针向中间移动,减少无效计算:
- 初始时,左指针在最左端(i=0),右指针在最右端(j=height.length-1),此时宽度最大。
- 计算当前盛水量,更新最大值。
- 移动指针:谁矮就移动谁(因为盛水量由矮的一边决定,移动高的一边只会让宽度减小,盛水量一定变小;而移动矮的一边可能遇到更高的垂线,盛水量可能增大)。
- 重复上述步骤,直到左右指针相遇。
为什么可行?
假设左指针i的高度小于右指针j的高度,此时若移动j,新的盛水量为min(height[i], height[j-1]) × (j-1-i),由于height[i]是限制因素,新水量只会小于等于原水量;而移动i,可能遇到更高的height[i+1],新水量可能增大。因此"移动较矮的指针"是最优选择。
三、Java代码实现(双指针法)public class Solution {
java
public int maxArea(int[] height) {
int left = 0; // 左指针,初始在最左端
int right = height.length - 1; // 右指针,初始在最右端
int maxArea = 0; // 记录最大盛水量
while (left < right) {
// 计算当前左右指针构成的容器的盛水量
int currentWidth = right - left;
int currentHeight = Math.min(height[left], height[right]);
int currentArea = currentWidth * currentHeight;
// 更新最大盛水量
maxArea = Math.max(maxArea, currentArea);
// 移动较矮的指针(贪心策略)
if (height[left] < height[right]) {
left++;
} else {
right--;
}
}
return maxArea;
}}
代码解析
- 指针初始化 :左指针
left从0开始,右指针right从数组末尾开始,确保初始宽度最大。 - 计算当前盛水量 :根据公式
宽度×最小高度计算,其中宽度是right - left,高度取左右指针高度的较小值。 - 更新最大值 :用
Math.max比较当前盛水量和历史最大值,保留较大值。 - 移动指针 :若左指针高度较低,则右移左指针;否则左移右指针,直到两指针相遇(
left < right条件不满足)。 - 返回结果 :遍历结束后,
maxArea即为最大盛水量。
四、测试案例验证
测试案例1:基础示例
输入:height = [1,8,6,2,5,4,8,3,7]
处理过程:
- 初始:left=0(h=1),right=8(h=7),面积=8×1=8,max=8 → 移动left(1<7)
- left=1(h=8),right=8(h=7),面积=7×7=49,max=49 → 移动right(7<8)
- left=1(h=8),right=7(h=3),面积=6×3=18 <49 → 移动right
- ...(后续步骤省略)
- 最终max=49,正确。
测试案例2:最短示例
输入:height = [1,1]
处理:left=0,right=1,面积=1×1=1,移动任意指针后循环结束,输出1,正确。
五、复杂度分析
- 时间复杂度:O(n)。左右指针从两端向中间移动,每个元素最多被访问一次,总操作次数为n级。
- 空间复杂度:O(1)。仅使用常数个额外变量,无额外空间开销。
六、总结
"盛最多水的容器"的解题关键是双指针+贪心策略,核心要点如下:
- 盛水量由"宽度"和"最小高度"共同决定,初始时宽度最大。
- 移动较矮的指针是最优选择,因为这是唯一可能使盛水量增大的方式。
- 双指针法将时间复杂度从O(n²)降至O(n),高效解决大数据量问题。
这道题的双指针技巧具有通用性,可迁移到其他"范围查找最大值"的问题中。下一篇我们继续讲解LeetCode热题100的下一道题。