PyTorch的AI框架小白入门的学习点

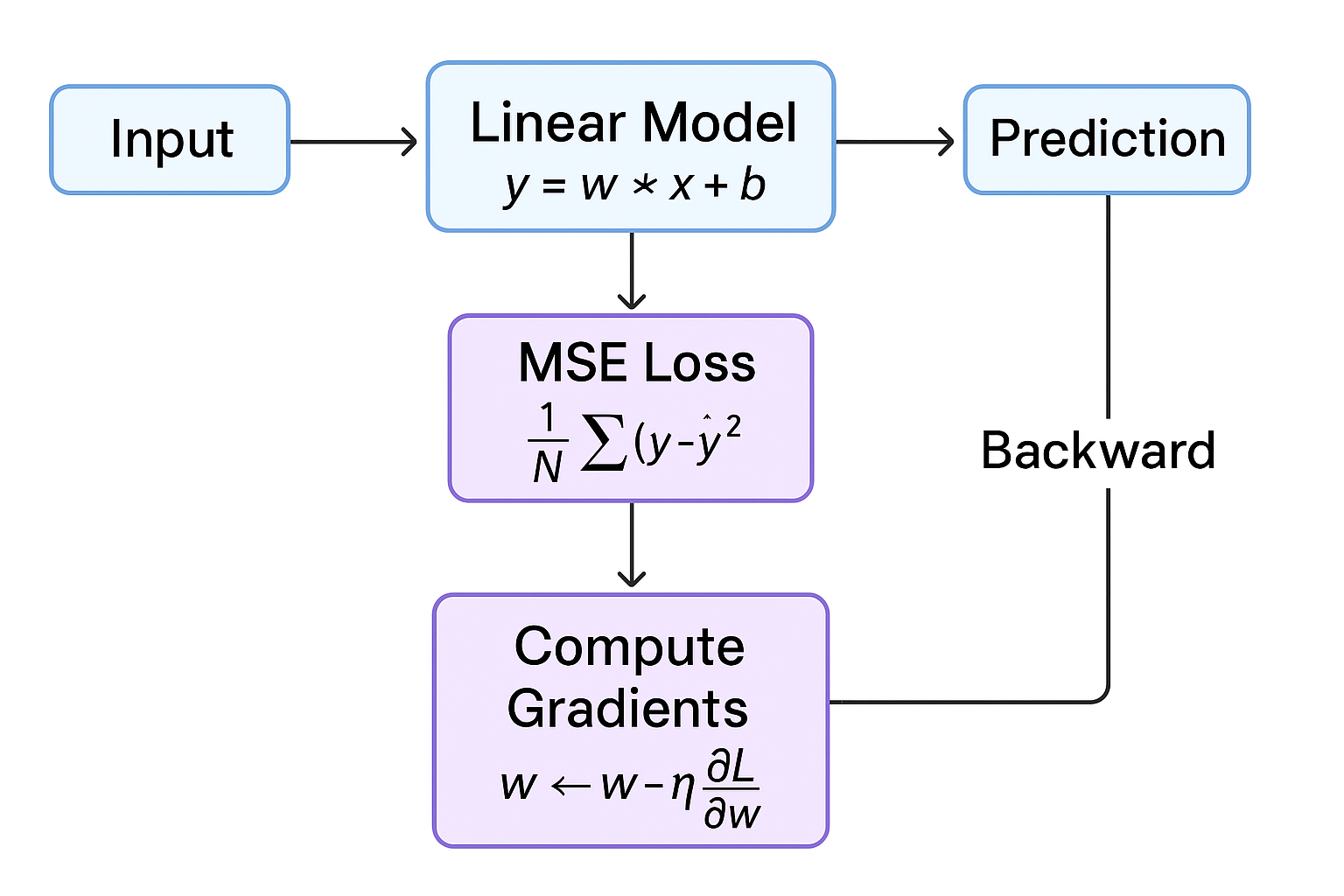
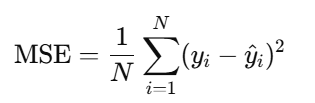逐行详解（重点解释你问的函数）

下面把你那段代码逐行注释并解释每个函数/调用的作用，同时给出一些形状、数学公式和调试技巧，帮助你"真正看懂"训练过程。

import torch
import torch.nn as nn
import torch.optim as optim

# -----------------------
# 1. 数据（y = 2x + 1）
# -----------------------
x = torch.randn(100, 1)    # torch.randn(n, d) -> 从标准正态分布采样，返回形状为 (100,1) 的张量
y = 2 * x + 1              # 按元素运算，y 的形状同 x，表示我们要拟合的目标函数

# -----------------------
# 2. 模型
# -----------------------
model = nn.Linear(1, 1)    # 全连接线性层：y = x * W^T + b
                           # in_features=1, out_features=1
                           # model.weight.shape == [out_features, in_features] -> [1,1]
                           # model.bias.shape == [out_features] -> [1]

# -----------------------
# 3. 损失 + 优化器
# -----------------------
criterion = nn.MSELoss()               # 均方误差损失：默认 reduction='mean'
                                       # loss = (1/N) * sum_i (y_pred_i - y_i)^2

optimizer = optim.SGD(model.parameters(), lr=0.1)
# optim.SGD(...) 创建一个随机梯度下降优化器
# model.parameters() 返回模型中所有可学习参数（weight, bias）
# lr=0.1 是学习率

# -----------------------
# 4. 训练循环
# -----------------------
for epoch in range(100):
    y_pred = model(x)                 # 等价于 model.forward(x)
                                      # 输入 x (shape [100,1]) -> 输出 y_pred (shape [100,1])

    loss = criterion(y_pred, y)       # 计算 MSE Loss（标量）

    optimizer.zero_grad()             # 清零所有参数的梯度（非常重要，PyTorch 默认梯度是累加的）
    loss.backward()                   # 自动求导：计算 loss 对参数的梯度，结果存到 param.grad
    optimizer.step()                  # 根据 param.grad 更新参数（SGD：param -= lr * grad）

# -----------------------
# 5. 查看训练结果
# -----------------------
print(model.weight, model.bias)       # 打印训练后的权重和偏置（接近 2 和 1）

---

关键函数与概念详解（逐项）

torch.randn(100, 1)

• 从标准正态分布采样（均值0，方差1）。返回 torch.FloatTensor，形状 (100,1)。通常作为随机输入或初始化数据。

nn.Linear(in_features, out_features)

• 创建一个线性（全连接）层，内部有两个 Parameter：weight（形状 [out_features, in_features]）和 bias（形状 [out_features]）。计算 y = x @ weight.T + bias（@ 表示矩阵乘法）。

nn.MSELoss()

• 均方误差损失。默认 reduction='mean'，所以
  

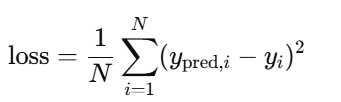
  对于输出为 (100,1)，它会对所有元素取均值。

optim.SGD(model.parameters(), lr=0.1)

• 随机梯度下降优化器。model.parameters() 给出要更新的参数集合（weight 和 bias）。默认没有 momentum、没有 weight decay。
• 在每次 optimizer.step() 时，执行类似：
  θ←θ−lr⋅θ.grad

model(x)

• 等价于 model.forward(x)。触发模块的前向计算，返回一个 Tensor（其 requires_grad=True，并带 grad_fn，表示图上这个张量由哪些操作产生）。

optimizer.zero_grad()

• 清零模型所有参数的 .grad。因为 PyTorch 的梯度是累加的（默认行为），如果不在每次更新前清零，会把多个 iteration 的梯度叠加在一起，导致错误更新。

loss.backward()

• 核心的自动求导调用。它从 loss 节点沿计算图反向传播，计算出每个叶子张量（通常是 Parameter）的梯度并把结果累放到 param.grad。
• 对于本例（线性回归），数学公式为：
  

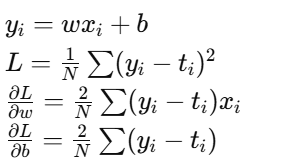
optimizer.step()

• 使用当前参数的 .grad 来更新参数（按优化器规则）。SGD 情况下执行 ( \theta \gets \theta - \text{lr} \cdot \theta.\text{grad} )。

---

训练过程从数学角度的简短流程

调试与观察技巧（好用）

• 查看当前梯度：在 loss.backward() 之后可以打印 model.weight.grad / model.bias.grad 看数值与形状。

  loss.backward()
  print(model.weight.grad, model.bias.grad)

• 不想计算梯度（推理）：用 with torch.no_grad(): 包裹预测代码以节省内存。

• 切换推理模式（用于 dropout/batchnorm）：model.eval()（训练时用 model.train()）。虽然线性层本身不受影响，但养成好习惯。

• 若想在中途保存训练进度：torch.save(model.state_dict(), "ckpt.pth")，以后用 load_state_dict 恢复。

• 若想查看训练过程（loss 曲线），在循环里记录 loss.item() 并画图。

---

为什么最后打印 model.weight, model.bias 会接近 2 和 1？

因为目标是 y = 2x + 1，通过多次迭代（且数据完整覆盖），优化器会调整 w 和 b，使得预测最小化 MSE，从而 w → 2，b → 1（近似）。

---

什么是张量，什么是均方误差损失，什么是学习率，

---

1️⃣ 张量（Tensor）

🔹 定义

张量就是一种多维数组 ，它是 PyTorch 的基础数据结构。

可以理解为：

• 0 维张量 → 标量（一个数字）
• 1 维张量 → 向量（一个数字列表）
• 2 维张量 → 矩阵
• 3 维张量 → 图像（通道 × 高 × 宽）
• ... 多维张量 → 任意维度的数据集合

🔹 PyTorch 张量特点

1. 可以像 NumPy 数组一样做数学运算（加、减、乘、矩阵乘法...）
2. 可以记录梯度，用于自动求导 (requires_grad=True)
3. 可以直接在 GPU 上计算，支持大规模并行运算

🔹 举例

import torch

# 标量
a = torch.tensor(3.0)       # 0维
print(a.shape)  # torch.Size([])

# 向量
v = torch.tensor([1.0, 2.0, 3.0])  # 1维
print(v.shape)  # torch.Size([3])

# 矩阵
m = torch.tensor([[1.0, 2.0], [3.0, 4.0]])  # 2维
print(m.shape)  # torch.Size([2,2])

# 三维张量（如一张 RGB 图片）
img = torch.randn(3, 64, 64)  # 通道 3, 高 64, 宽 64
print(img.shape)  # torch.Size([3,64,64])

在深度学习中，模型的输入、输出和参数（weight、bias）都是张量。

---

2️⃣ 均方误差损失（MSE Loss）

🔹 定义

均方误差损失（Mean Squared Error Loss）是回归问题常用的损失函数。

它衡量模型预测值 y_pred 与真实值 y 的差距：

🔹 解释

• 对每个样本求平方误差 (预测值 - 真实值)^2
• 再对所有样本取平均
• 越小 → 模型预测越接近真实值

🔹 举例

import torch
import torch.nn as nn

y_true = torch.tensor([1.0, 2.0, 3.0])
y_pred = torch.tensor([1.5, 2.5, 2.0])

criterion = nn.MSELoss()
loss = criterion(y_pred, y_true)
print(loss)  # 输出：0.4167

在训练过程中，我们用 MSE 来告诉模型"预测错了多少"，然后模型通过梯度下降调整参数。

---

3️⃣ 学习率（Learning Rate）

🔹 定义

学习率是优化器的一个超参数，表示每次参数更新的步长 。

数学公式：

0 <--- 0 - η * ∂L/∂θ

• θ → 参数（weight、bias）
• η → 学习率
• ∂L/∂θ → 梯度

🔹 作用

• 学习率大 → 每次更新幅度大 → 训练可能更快，但可能不稳定、震荡
• 学习率小 → 每次更新幅度小 → 训练更稳定，但可能收敛慢

🔹 举例

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)  # lr=0.1 就是学习率

在训练时，PyTorch 会自动用：

param = param - lr * param.grad

去更新参数。

🔹 小技巧

• 通常用 0.001 ~ 0.1 的范围调试
• 训练大模型时常用 学习率衰减 或 自适应优化器（Adam, RMSProp）
• 如果 loss 不下降或震荡 → 尝试调小学习率

---

🔹 总结（最核心概念）

概念	定义	作用
张量 (Tensor)	多维数组，可存梯度，可 GPU 计算	模型输入、输出、参数
均方误差损失 (MSE)	平方误差平均值	衡量预测值与真实值差距
学习率 (lr)	参数更新步长	控制梯度下降速度，影响收敛稳定性

---

关系图

• 张量：输入 x、输出 y、权重 w、偏置 b
• 前向计算：y_pred = x * w + b
• 损失：MSE Loss
• 反向传播：梯度 ∂L/∂w, ∂L/∂b
• 优化器：使用 学习率 更新参数

生成的流程图会清晰展示训练循环：输入 → 前向 → 损失 → 梯度 → 更新 → 下一轮。