小米笔试题：一元一次方程求解

输入一个一元一次方程求解：

例如 3a+6=2a-3

a=-9

1：拆分等式

把等式按 =分成左右两部分，比如：

左边（left）："3x + 5"
右边（right）："2x - 7"

2：解析表达式，提取 x 的系数和常数

我们需要分别解析左边和右边的表达式，统计：

所有含 x项的系数总和 → 记作 coefficientOfX
所有常数项的总和 → 记作 constantTerm

比如：

对于 "3x + 5"：
- x 系数：3
- 常数：+5
对于 "2x - 7"：
- x 系数：2
- 常数：-7

但我们要把整个等式看作：

(左边) = (右边) => (左边) - (右边) = 0

因此，我们可以这样处理：

把左边的 x 系数和常数加到总和中
把右边的 x 系数和常数 减去（即加负值）

最终得到：

总的 x 系数：leftX + rightX * (-1)
总的常数：leftConst + rightConst * (-1)

这样就能转化为标准形式

3：解析单个表达式（如 "3x + 5" 或 "2x - 7"）

这是比较复杂的一步，因为你要从字符串中提取出：

哪些是带 x 的项（如 3x, -x, +2x）
哪些是纯数字常数（如 5, -7, +10）

(a)x + (b) = 0

然后解就是：

x = -b / a

小技巧：

可以先用正则表达式或按空格分割后分析每一项
或者更简单地，去掉所有空格 ，然后按 +和 -来切分项（注意第一个项可能没有符号，默认为 +

系数解析代码：

java 复制代码

public static int[] parseExpression(String expr) {
            int coeffX = 0; // x的系数
            int constant = 0; // 常数项

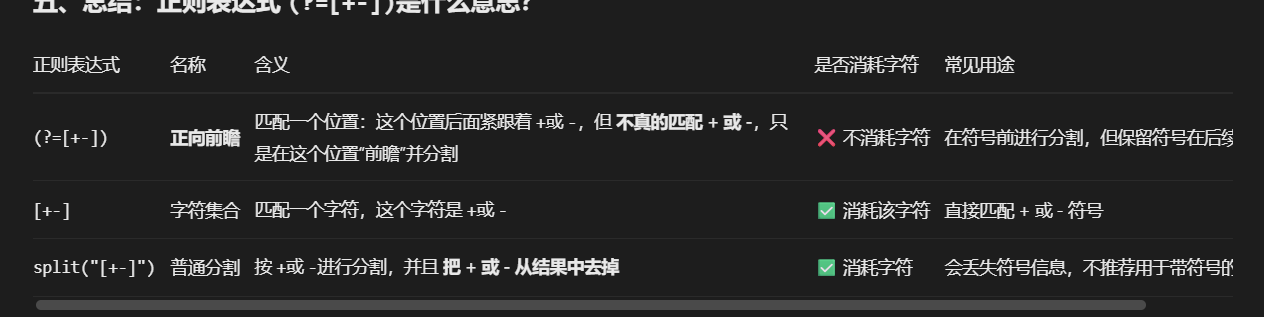
            String[] tokens = expr.split("(?=[+-])"); // 在 + - 前分割

            for (String token : tokens) {
                if (token.isEmpty()) continue;

                if (token.contains("x")) {
                    // 处理x项，如 "3x", "-x", "+2x", "x"
                    String numPart = token.replace("x", "");
                    int coef = 1;
                    if (numPart.isEmpty() || numPart.equals("+")) {
                        coef = 1;
                    } else if (numPart.equals("-")) {
                        coef = -1;
                    } else {
                        coef = Integer.parseInt(numPart);
                    }
                    coeffX += coef;
                } else {
                    // 处理常数项，如 "5", "-3", "+10"
                    if (!token.isEmpty()) {
                        constant += Integer.parseInt(token);
                    }
                }
            }

            return new int[]{coeffX, constant};
        }

主流程代码

java 复制代码

 public static void main(String[] args) {
            Scanner scanner = new Scanner(System.in);
            System.out.println("请输入一元一次方程（如：3x + 5 = 2x - 7）：");
            String equation = scanner.nextLine().replaceAll("\\s+", ""); // 去掉所有空格

            try {
                String[] parts = equation.split("=");
                if (parts.length != 2) {
                    System.out.println("方程格式错误：必须包含一个等号");
                    return;
                }

                String leftExpr = parts[0];
                String rightExpr = parts[1];

                // 解析表达式，返回 x的系数 和 常数
                int[] left = parseExpression(leftExpr);
                int[] right = parseExpression(rightExpr);

                // 标准化：移到左边 => left - right = 0
                int totalX = left[0] - right[0];
                int totalConst = left[1] - right[1];

                System.out.printf("化简后： %dx + %d = 0%n", totalX, totalConst);

                if (totalX == 0) {
                    if (totalConst == 0) {
                        System.out.println("方程恒成立，x可以为任意实数");
                    } else {
                        System.out.println("方程无解");
                    }
                } else {
                    double x = (double) -totalConst / totalX;
                    System.out.printf("解为：x = %.3f%n", x);
                }

            } catch (Exception e) {
                System.out.println("输入格式错误，请检查方程格式");
            }
        }