二叉树的层序遍历

以下内容是从网站中学习的，如果有错误欢迎批评指正~~

学会二叉树的层序遍历，可以一口气打完以下十题：

给你一个二叉树，请你返回按层序遍历得到的节点值。（即逐层的，从左到右访问所有节点）。

思路

二叉树的层序遍历，就是从左到右一层一层的去遍历二叉树。这种遍历方式和我们之前讲过的都不太一样。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历的方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

代码：

复制代码

//二叉树的层序遍历
class Solution{
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();

    public List<List<Integer>> levelOrder(TreeNode root){
        checkFun(root);
        return resList;
    }

    //BFS--迭代方式--借助队列
    public void checkFun(TreeNode node){
        if(node == null) return;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(node);

        while(!que.isEmpty()){
            List<Integer> itemList = new ArrayList<Integer>();
            int len = que.size();
            while(len > 0){
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);
                if(tmpNode.left != null){
                    que.offer(tmpNode.left);
                }
                if(tmpNode.right != null){
                    que.offer(tmpNode.right);
                }
                len--;
            }
            resList.add(itemList);
        }
    }
}

返回值的方式：

复制代码

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        return checkFun(root); // 直接返回方法结果
    }
    
    public List<List<Integer>> checkFun(TreeNode node) {
        List<List<Integer>> resList = new ArrayList<>();
        if (node == null) return resList;
        
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(node);
        
        while (!que.isEmpty()) {
            List<Integer> itemList = new ArrayList<>();
            int len = que.size();
            while (len > 0) {
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);
                if (tmpNode.left != null) que.offer(tmpNode.left);
                if (tmpNode.right != null) que.offer(tmpNode.right);
                len--;
            }
            resList.add(itemList);
        }
        return resList;
    }
}

二叉树的层序遍历II

给定一个二叉树，返回其节点值自底向上的层次遍历。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

相对于上面那一道题，就是最后把result数组反转一下就可以了。

代码如下：

复制代码

// 二叉树的层序遍历II

public class N0107{
    //解法：队列，迭代。层序遍历
    public List<List<Integer>> solution(TreeNode root){
    //利用双向链表可以进行O(1)头部插入，这样最后答案不需要再反转
        LinkedList<List<Integer>> ans = new LinkedList<>();

        Queue<TreeNode> q = new LinkedList<>();

        if(root != null) q.offer(root);
        while(!q.isEmpty()){
            int size = q.size();

            List<Integer> temp = new ArrayList<>();

            for(int i = 0;i < size ;i ++){
                TreeNode node  = q.poll();
                temp.add(node.val);

                if(node.left != null) q.offer(node.left);
                if(node.right != null) q.offer(node.right);
            }
            ans.addFirst(temp);
        }
        return ans;
    }
}

二叉树的右视图

给定一棵二叉树，想象自己站在他的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

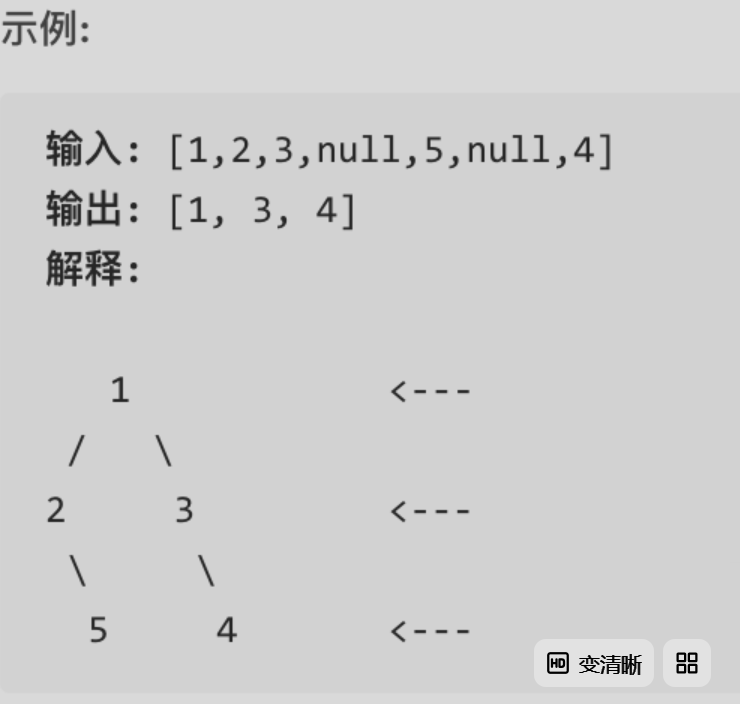
思路

层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以了。

复制代码

// 二叉树的右视图

public class N0199{
    //解法：队列，迭代，每次返回每层的最后一个字段即可，小优化：每层右孩子先入队，代码略

    public List<Integer> rightSideView(TreeNode root){
        List<Integer> list = new ArrayList<>();
        Deque<TreeNode> que = new LinkedList<>();

        if(root == null){
            return list;
        }

        que.offerLast(root);
        while(!que.isEmpty()){
            int size = que.size();
            for(int i = 0;i < size;i ++){
                TreeNode poll = que.pollFirst();
                if(poll.left != null){
                    que.addLast(poll.left);
                }
                if(poll.right != null){
                    que.addLast(poll.right);
                }
                if(i == size - 1){
                    list.add(poll.val);
                }
            }
        }
        return list;
    }
}

二叉树的层平均值

给定一个非空二叉树，返回一个由每层节点平均值组成的数组。

思路

本题就是层序遍历的时候把一层求个总和再取一个均值。

复制代码

//二叉树的层平均值

public class N0637{

    //解法：队列，迭代，每次返回每层的最后一个字段即可。
    public List<Double> averageOfLevels(TreeNode root) { 
        List<Double> list = new  ArrayList<>();
        Deque<TreeNode> que = new LinkedList<>();
        
        if(root == null){
            return list;
        }
        
        que.offerLast(root);
        while(!que.isEmpty()){
            int size = que.size();
            double sum = 0.0;
            for(int i = 0;i < size;i ++){
                TreeNode poll = que.pollFirst();
                sum += poll.val;
                if(poll.left != null){
                    que.addLast(poll.left);
                }
                if(poll.right != null){
                    que.addLast(poll.right)
                }
            }
            list.add(sum / size);
        }
        return list;
    }
}

填充每个节点的下一个右侧节点指针

给定一个满二叉树，其所有叶子节点都在同一层，每个父节点都有两个字节点。二叉树定义如下：

复制代码

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充他的每个next指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将next指针设置为null。

初始状态下，所有next指针都被设置为null。

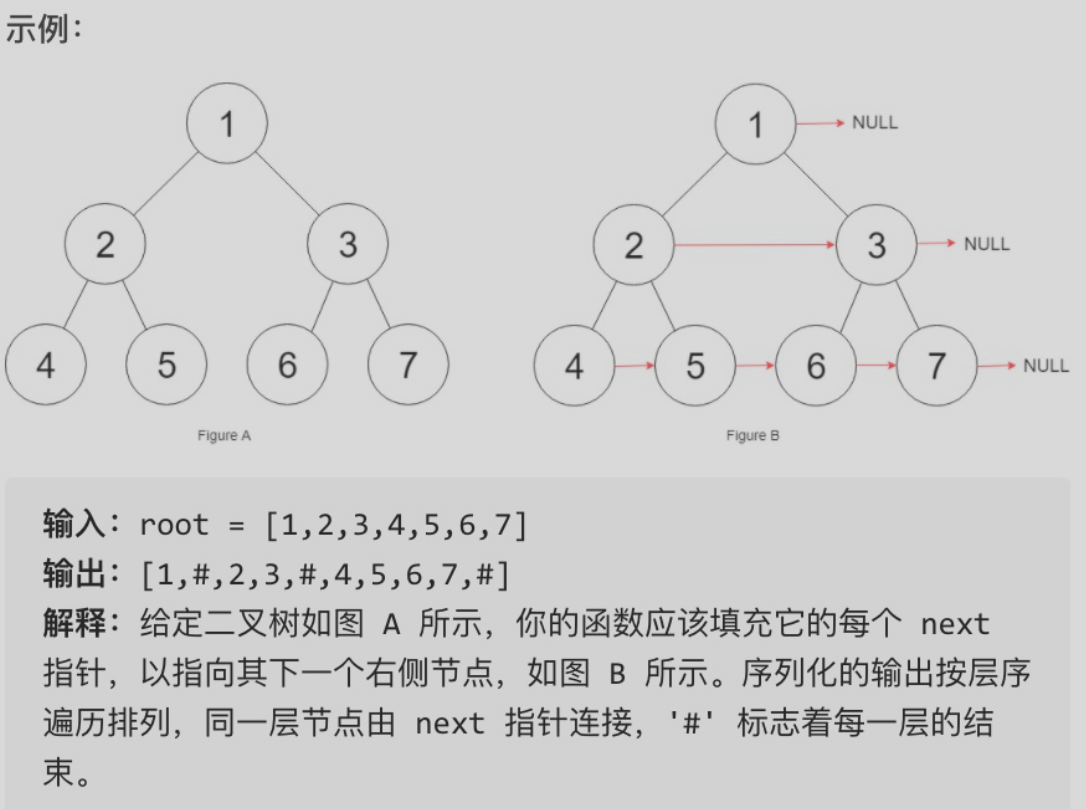
思路

本题依然是层序遍历，只不过在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以了。

复制代码

class Solution{
    public Node connect(Node root){
        Queue<Node> q = new LinkedList<Node>();
        if(root != null) q.add(root);

        while(q.size() != 0){
            int size = q.size();

            Node cur = q.poll();
            if(cur.left != null) q.add(cur.left);
            if(cur.right != null) q.add(cur.right);
            for(int i = 1;i < size;i ++){
                Node next = q.poll();
                if(next.left != null)
                    q.add(next.left);
                    if(next.right != null)
                        q.add(next.right);
                        cur.next = next;
                        cur = next;
            }
        }
        return root;
    }
}

填充每个节点的下一个右侧节点指针II

思路

这道题目说的是二叉树，但上道题目说的是满二叉树，其实没有任何差别，一样的代码，一样的逻辑。

复制代码

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}
    
    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/
class Solution {
    public Node connect(Node root) {
	Queue<Node> tmpQueue = new LinkedList<Node>();
	if (root != null) tmpQueue.add(root);

	while (tmpQueue.size() != 0){
	    int size = tmpQueue.size();

            Node cur = tmpQueue.poll();
            if (cur.left != null) tmpQueue.add(cur.left);
            if (cur.right != null) tmpQueue.add(cur.right);

	    for (int index = 1; index < size; index++){
		Node next = tmpQueue.poll();
		if (next.left != null) tmpQueue.add(next.left);
		if (next.right != null) tmpQueue.add(next.right);

                cur.next = next;
                cur = next;
	    }
	}

        return root;
    }
}

二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：

给定二叉树 [3,9,20,null,null,15,7]，

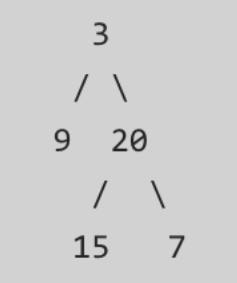
返回它的最大深度 3 。

思路

使用迭代法的话，使用层序遍历是最为合适的，因为最大深度就是二叉树的层数，和层序遍历的方式极其吻合。

在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：

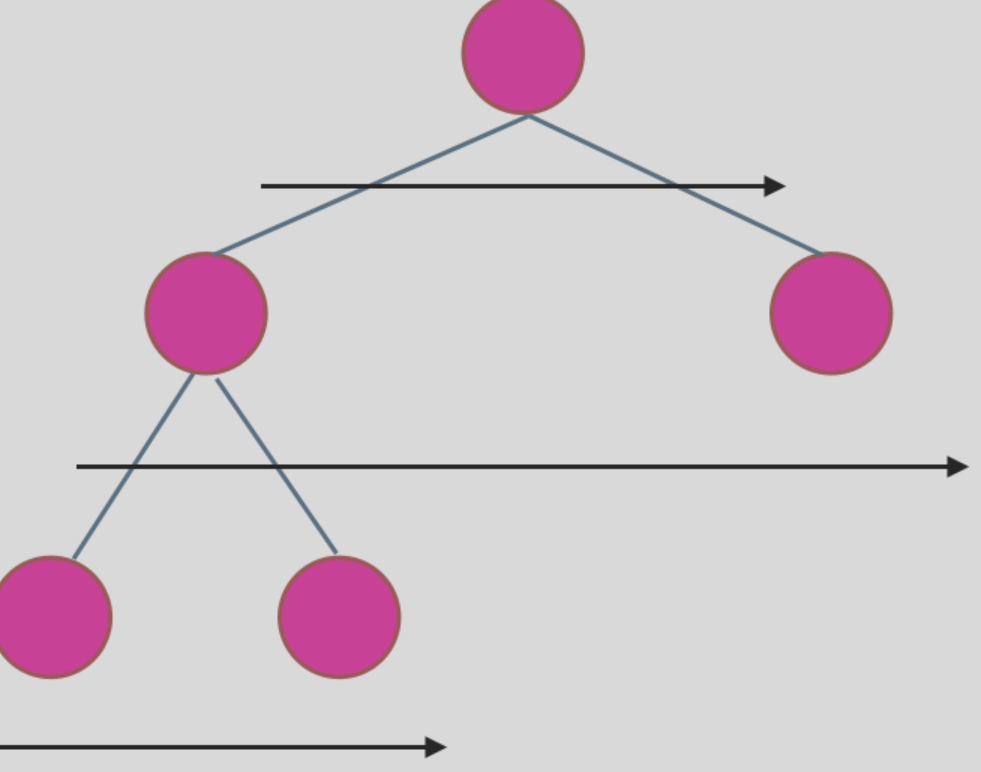
所以这道题的迭代法就是一道模板题，可以使用二叉树层序遍历的模板来解决的。

复制代码

class Solution{
    public int maxDepth(TreeNode root){
        if(root == null) return 0;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        int depth = 0;
        while(!que.isEmpty()){
            int size = que.size();
            while(size > 0){
                TreeNode node = que.poll();
                if(node.left != null) que.offer(node.left);
                if(node.right != null) que.offer(node.right);
                size--;
            }
            depth++;
        }
        return depth;
    }
}

二叉树的最小深度

相对于 104.二叉树的最大深度，本题还也可以使用层序遍历的方式来解决，思路是一样的。

需要注意的是，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

复制代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minDepth(TreeNode root){
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;
        while (!queue.isEmpty()){
            int size = queue.size();
            depth++;
            for (int i = 0; i < size; i++) {
               TreeNode cur = queue.poll();
                //如果当前节点的左右孩子都为空，直接返回最小深度
                if (cur.left == null && cur.right == null){
                    return depth;
                }
                if (cur.left != null) queue.offer(cur.left);
                if (cur.right != null) queue.offer(cur.right);
            }
        }
        return depth;
    }
}