优先级队列

优先级队列(PriorityQueue)：返回最⾼优先级对象，添加新的对象

核心特性

有序出队 ：poll() 和 peek() 操作总是返回并移除（或查看）优先级最高（或最低，取决于排序规则）的元素
基于堆 ：内部使用堆（通常是最小堆）来维护元素顺序，确保 O(log n) 的插入和删除时间复杂度
无界队列：容量可以动态增长

堆的概念

堆：一种特殊的树形数据结构，大堆+小堆

大堆：对于大堆中的任意节点 i （除了叶节点）的值都大于或等于其左右孩子节点的值

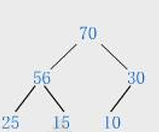
小堆：对于小堆中的任意节点 i （除了叶节点）的值都小于或等于其左右孩子节点的值

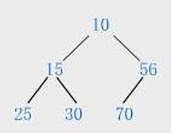
堆的性质

堆中某个节点的值总是不⼤于或不⼩于其⽗节点的值

堆总是⼀棵完全⼆叉树

堆的存储方式

堆是一颗完全二叉树，层序的规则采用顺序方式来高效存储

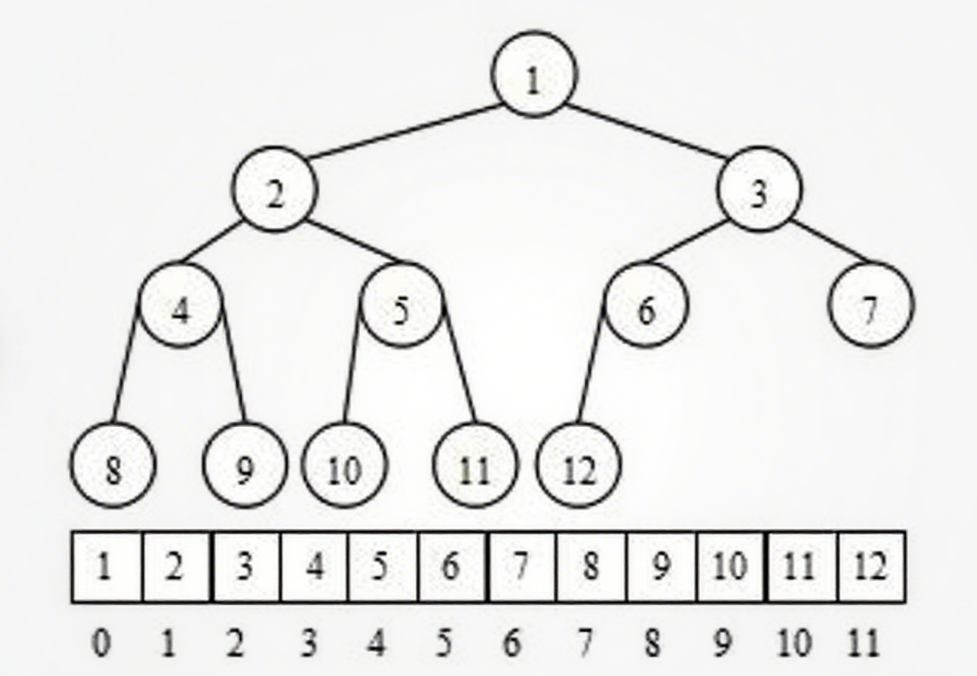
假设i为节点在数组的下标：

若i=0，则i表示的节点为根节点，否则i节点的双亲节点为(i-1)/2

若2*i+1⼩于节点个数，则节点i的左孩⼦下标为2*i+1，否则没有左孩子

若2*i+2⼩于节点个数，则节点i的左孩⼦下标为2*i+2，否则没有右孩子

堆的创建

java 复制代码

public int[] array;
public int usedSize;
public PriorityQueueHeap(){
    this.array=new int[5];
}
public void createArray(int[] arr){
    for (int i = 0; i <arr.length ; i++) {
        array[i]=arr[i];
        usedSize++;
    }
}
public void createHeap(int[] array){
    for (int parent=(usedSize-1-1)/2; parent>=0 ; parent--) {
        downadjust(array,usedSize);
    }
}

复制代码

堆的调整

/*向下调整------大根堆

每颗子树的根节点parent

每棵子树是否调整结束的位置usedSise

* */

java 复制代码

private void downadjust(int[] array, int parent) {
     int child=2*parent+1;
     while(child<usedSize){//至少有一个左孩子
         if (child+1<usedSize&&array[child]<array[child+1]){
             child++;//child下标一定是最大孩子的下标
         }
         if (array[child]>array[parent]){
             swap(array,child,parent);
             parent=child;
             child=2*parent+1;
         }else{
             break;
         }
     }
}
private void swap(int[] array,int i,int j){
     int temp=array[i];
     array[i]=array[j];
     array[j]=temp;
}
//向上调整
public void upAdjust(int child){
    int parent=(child-1)/2;
    while(parent>=0){
        if (array[child]>array[parent]){
            swap(array,child,parent);
            child=parent;
            parent=(child-1)/2;
        }else {
            break;
        }
    }
}

堆的插入

java 复制代码

public void push(int val){
    if (isFull()){
        grow(array);
    }
    array[usedSize]=val;
    upAdjust(usedSize);
    usedSize++;
}

堆的删除

java 复制代码

public int delete(){
    if (isEmpty()){
        return -1;
    }
    int val=array[0];
    swap(array,0,usedSize-1);
    downAdjust(array,usedSize);
    return val;
}
public boolean isEmpty(){
    return usedSize==0;
}

堆的获取

java 复制代码

public int peek(){
    if (isEmpty()){
        return -1;
    }
    return array[0];
}

常用的方法

方法	描述
`boolean add(E e)` / `boolean offer(E e)`	将元素插入队列，`add()` 在失败时抛出异常，`offer()` 返回 `false`
`E poll()`	移除并返回队列头部（最高优先级）的元素。如果队列为空，返回 `null`
`E remove()`	移除并返回队列头部元素，如果队列为空，抛出 `NoSuchElementException`
`E peek()`	返回但不移除队列头部元素，如果为空，返回 `null`
`E element()`	返回但不移除队列头部元素，如果为空，抛出 `NoSuchElementException`。
`int size()`	返回队列中的元素数量
`boolean isEmpty()`	判断队列是否为空
`void clear()`	移除所有元素
`boolean contains(Object o)`	判断队列是否包含指定元素