算法7.0 - 技术栈

15. 三数之和 - 力扣（LeetCode）

审题：不同位置的三个数数字是可以相同的

是需要三个数的下标是不一样的

答案中不可以包含不重复的三元组：结合示例1 顺序不一样但是里面的元素相同算一种

三元组的顺序不重要：里面的元素的顺序不重要只要加起来是0就可以了

解法一：暴力解法排序+暴力枚举+利用set去重

在暴力解法的前提下总结最优解所以了解暴力解法是必须的

暴力枚举三元组的和然后去重如何完成去重操作？用set

至少三层for循环时间复杂度是n的立方

解法二：

先排序成为了有序数组触发关键词：二分双指针

和为s的两个数算法6.0的时候学习过可以用这个作为启示：

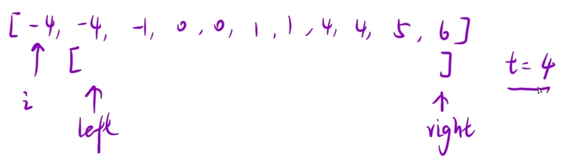
排序固定一个数在该数后面的区间内利用双指针算法快速找到两个和等于-1即可

但是这样并没有去重所以加一步

处理细节问题：

去重因为排序有相同的数字已经挨在一起了 1 22 3 有一个2后面的2就不需要了

依旧是找到一种结果后 left和right指针要跳过重复元素这样就去重了

固定的地方也需要去重

注意越界访问的情况

不漏（利用双指针算法的区间里面不漏）（找到情况后继续缩小区间寻）

小优化:固定的位置大于0了后面一定和为小于0的是没有的

逻辑不复杂代码细节很多

下面是效果图和代码：

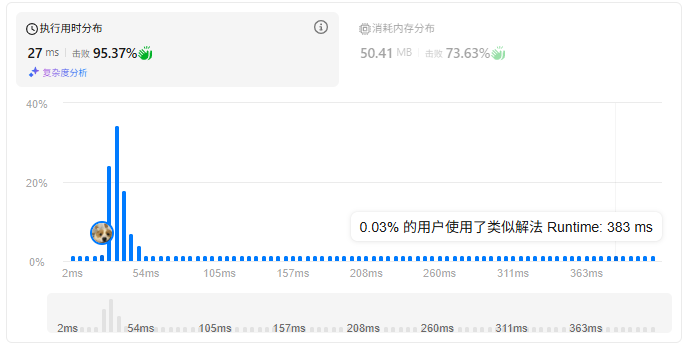
java 复制代码

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {

    //定义一个结果数组
    List<List<Integer>>  ret = new ArrayList<>();

    //排序
    Arrays.sort(nums);

    //利用双指针解决问题
    int n = nums.length;
    for(int i = 0; i<n ;) {
        if(nums[i]>0)  break;//小优化
        int left = i+1,right = n-1,target = -nums[i];

        while(left<right){
            int sum = nums[left]+nums[right];
            if(sum>target)  right--;
            else if(sum<target) left++;
            else {
                ret.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[left],nums[right])));
                 //缩小区间继续寻找
                left++;  
                right--;
                //去重
                //处理数组越界异常  条件里面加上一个判断left<right
                while(left<right && nums[left]==nums[left-1])  left++;
                while(left<right && nums[right]==nums[right+1]) right--;
               
            }
        }
        //去重固定的数
        i++;//for循环条件里面就是因为这个语句干掉的 
        while(i<n && nums[i]==nums[i-1]) i++;
    }
    return ret ; 
 }
}
//数组长度最后单独写一个变量定义  int n = arr.length;
//两数之和的时候  直接把target定义为负数  省去后面的绝对值的方法 
//定义一个结果数组 并且添加到数组里面的一种方法   List<List<Integer>>  ret = new ArrayList<>();  ret.add(new ArrayList<Integer>(Arrays.asList(nums[i],nums[left],nums[right])));
//有关去重的操作
//for循环里面的i++干掉  因为for循环逻辑执行之后里面固定数i已经往前面一步了  for里面的东西可以去掉

//xiyu20251012&1#1*7