heap
.概论
\;\;\;\;\;\;\;\; 本文解释堆
.堆
\;\;\;\;\;\;\;\; 堆是一颗完全二叉树[1](#1)。
二叉树所有的父节点值大于等于其子节点的值,或者父节点值小于等于其子节点的值。
堆分为大根堆和小根堆。
大根堆:父节点大于等于子节点
小根堆:父节点小于等于子节点
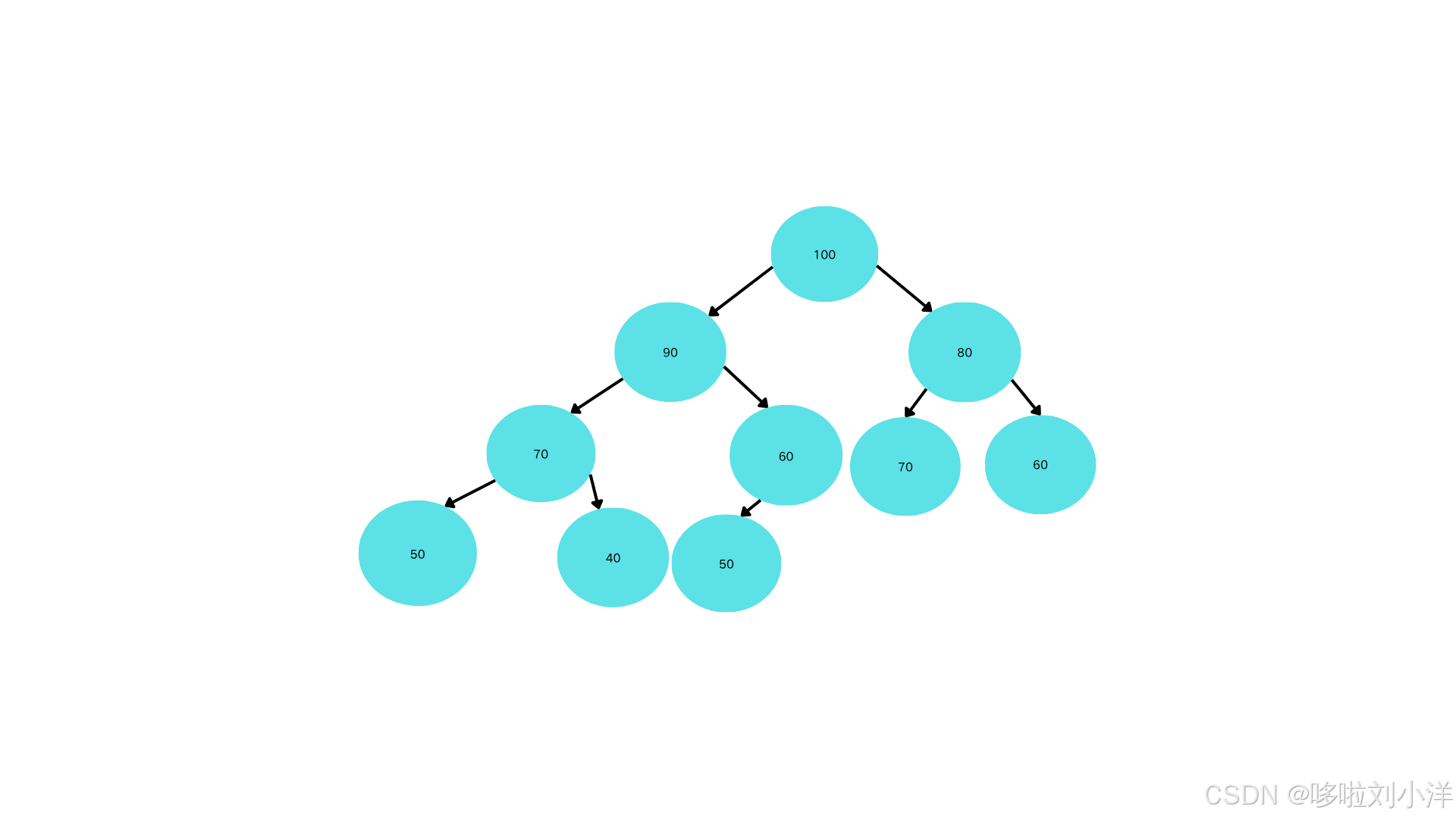
.大根堆的图示例
如图所示,所有的父节点都大于等于子节点(这棵树里面没有相同的节点,但仍然满足性质)。
.建堆
用数组存储堆
\;\;\;\;\;\;\;\; 因为堆的结构是一个完全二叉树,节点之间非常紧密,所以使用数组来存储。首先利用上图来构建一个堆(严格来说不是构建堆,因为上图就是一个堆,这是将堆用一种数据结构表示)。
我们利用二叉树上下两层的关系:左子节点的索引=父节点索引*2以及右子节点的索引=父节点索引*2+1来定义节点存储位置的关系:(首先建立一个数组a)
- 根节点对应索引1,即 a [ 1 ] = 100 a[1]=100 a[1]=100
- 根节点的左孩子节点对应的索引是: 父节点的索引 * 2=1 * 2=2, a [ 2 ] = 90 a[2]=90 a[2]=90
- 根节点的右孩子节点对应的索引是: 父节点的索引 * 2+1=1 * 2+1=3, a [ 3 ] = 80 a[3]=80 a[3]=80
- ...(依此类推)
最后生成的数组是:
a [ 11 ] = { 0 , 100 , 90 , 80 , 70 , 60 , 70 , 60 , 50 , 40 , 50 } a[11]=\{0,100,90,80,70,60,70,60,50,40,50\} a[11]={0,100,90,80,70,60,70,60,50,40,50}
如果对二叉树遍历有所了解的应该发现了,这其实就是一个层序遍历的过程。即:从上到下,从左往右,一个个遍历。
^^&&%%##
上述只是告诉堆是如何存储在数组中的。下面才是实际上的建堆
给定一个无序数组,用这个数组,构建一个大根堆(新数组)
给定数组(打乱上面示例数据) : n u m s = [ 70 , 50 , 90 , 80 , 60 , 100 , 50 , 40 , 70 , 60 ] nums=[70,50,90,80,60,100,50,40,70,60] nums=[70,50,90,80,60,100,50,40,70,60]。利用这个数组构建一个大根堆,为了理解堆的更新操作,只允许顺序遍历nums数组(以防聪明的朋友直接构建大根堆,这里假设nums是一个盲盒,每次只能取一个数)。
如图:
-
插入节点70
-

-
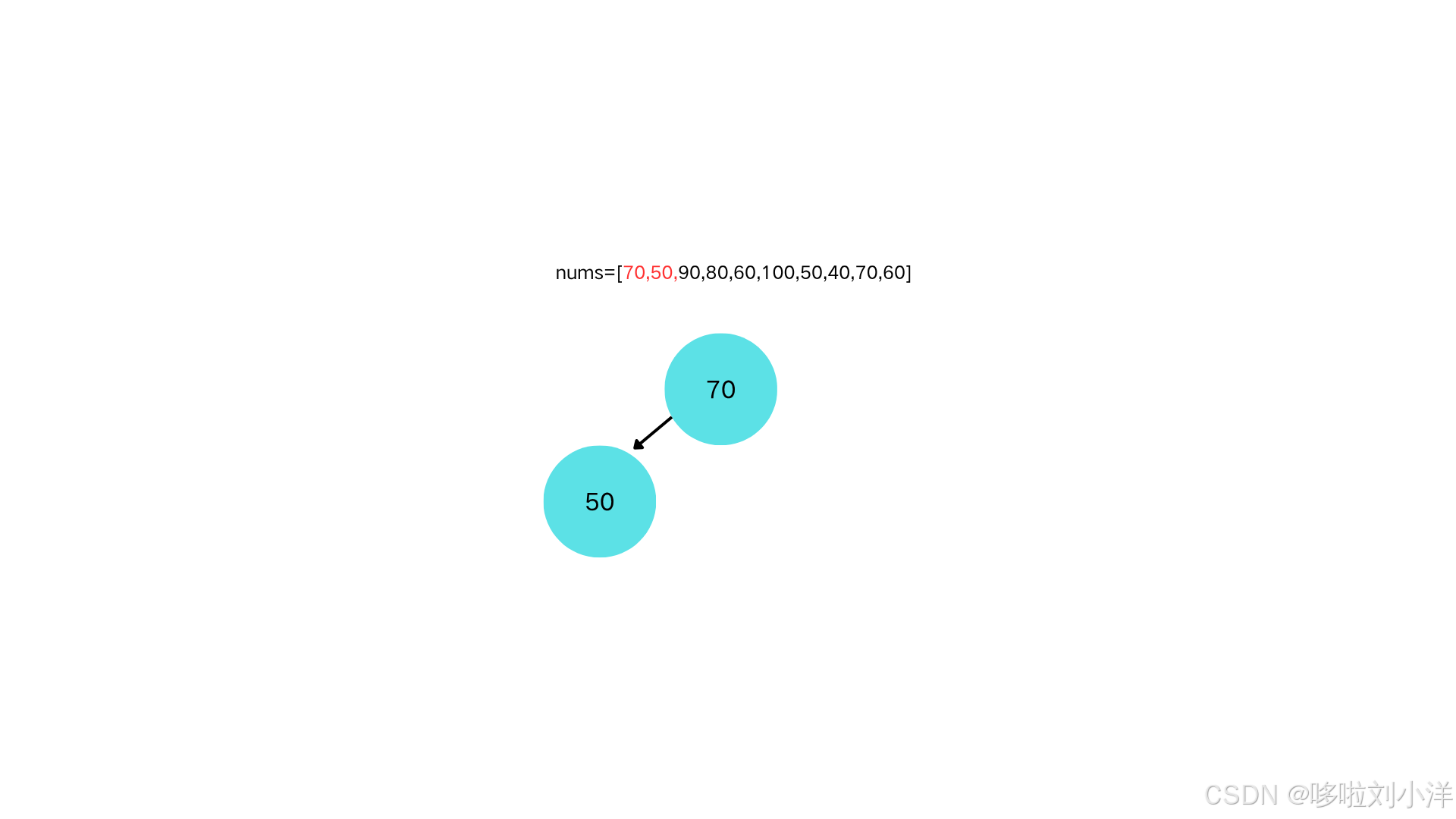
插入节点50,因为之前说过了,堆是一个完全二叉树,所以要插入到当前节点左子树来维护完全二叉树性质。并且满足大根堆性质,即父节点大于子节点,所以插入节点50需要和其父节点对比,50<70,所以不需要交换(也叫上浮)
-
-
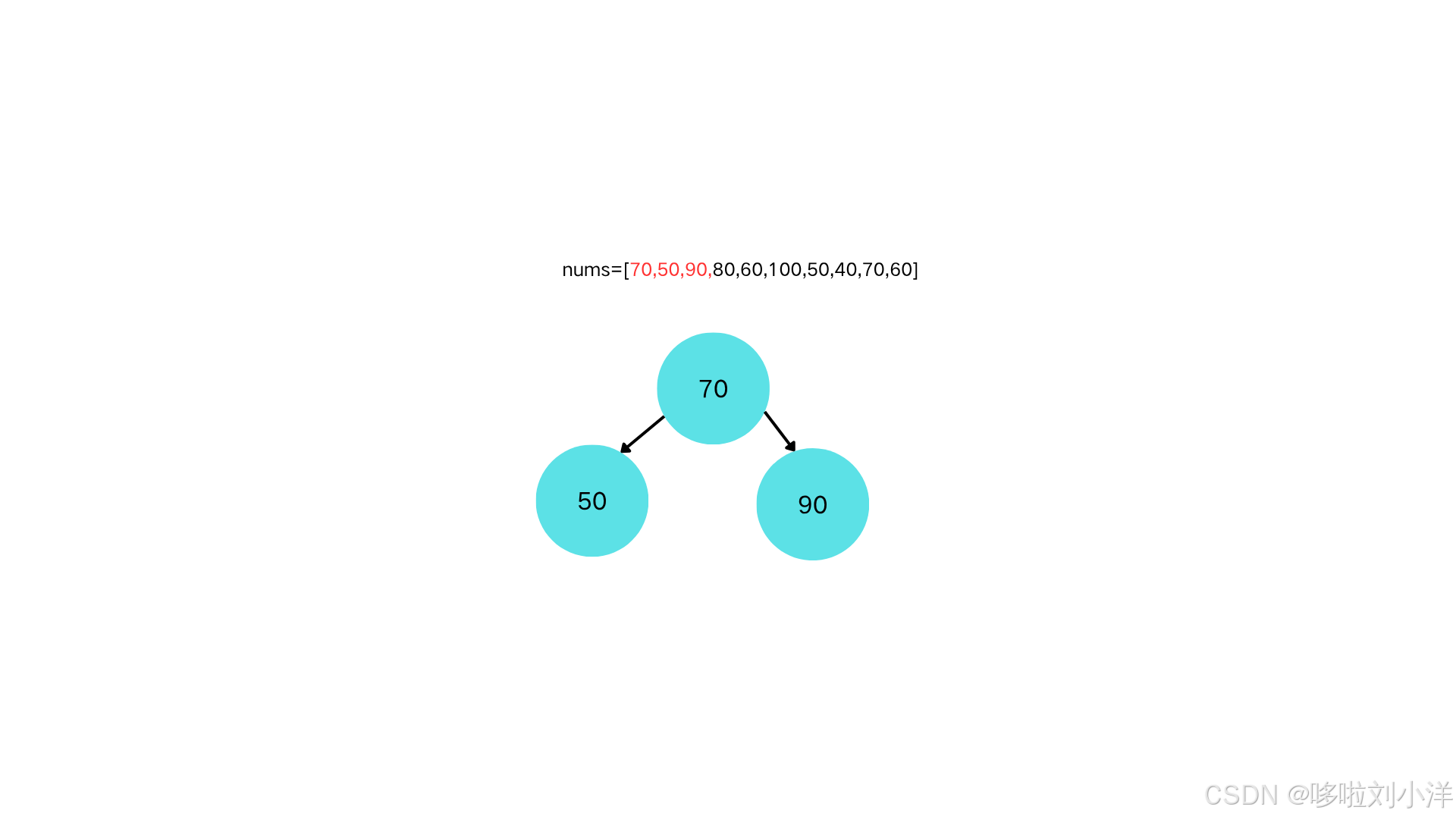
插入节点90,插入到二叉树层序遍历的最后一个元素的后面,即70的右子树(我们要构建完全二叉树)
-
-
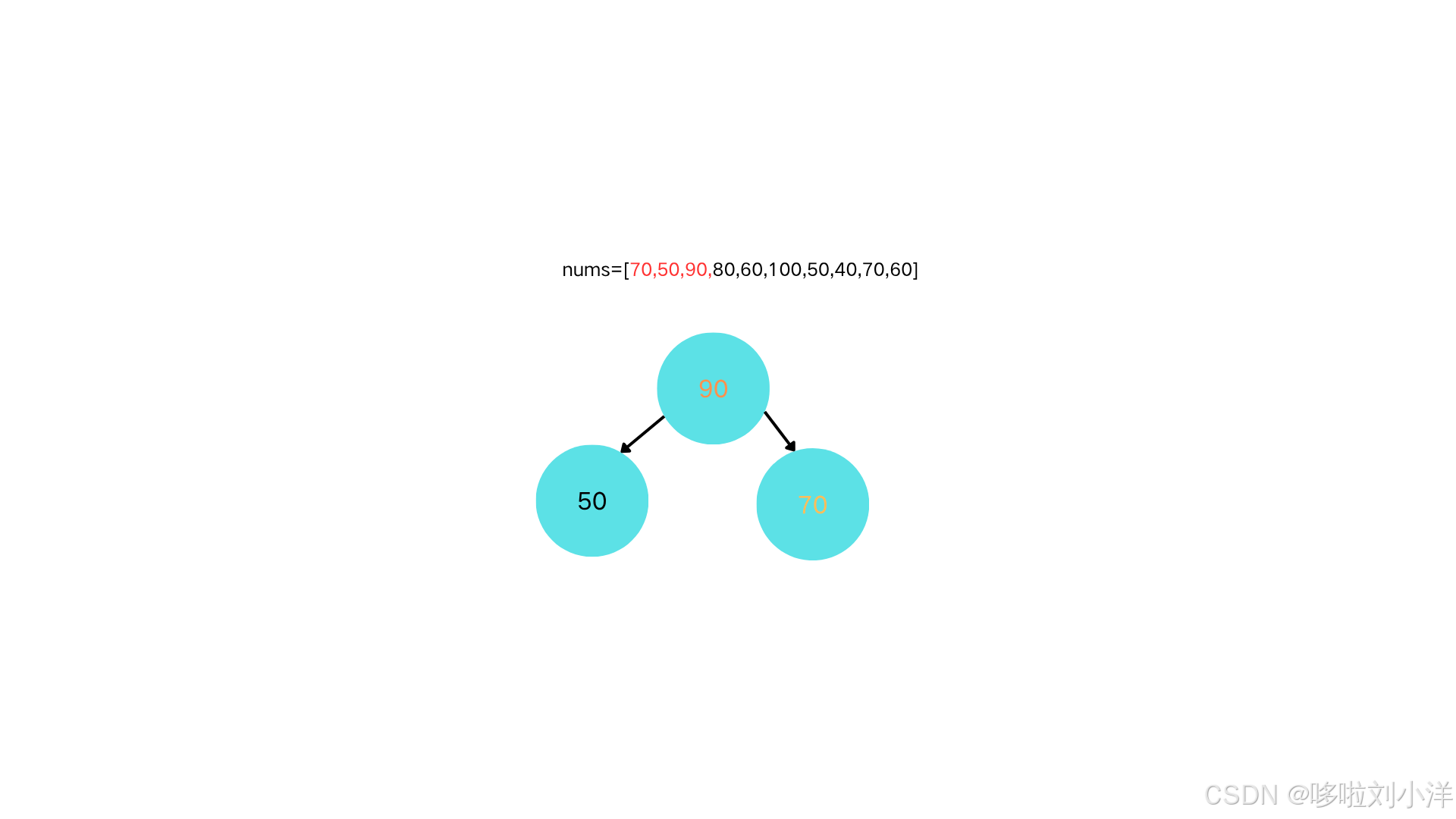
此时发现,当前二叉树虽然是完全二叉树,但是不满足大根堆的性质。因此要进行一个更新操作,即"上浮"操作。即"插入节点和它的最近父节点比较,如果比父节点大,就交换两者的位置。"
-
交换(70,90)两个节点后,二叉树就变成了标准的大根堆。
-
-
这里实际上有一个难点,有小朋友可能会有一点疑问:为什么交换两个节点后,堆的性质不会变?会不会对其它节点造成影响导致这个二叉树不满足堆的性质?答案是不会。点蓝色注脚2看解释[2](#这里实际上有一个难点,有小朋友可能会有一点疑问:为什么交换两个节点后,堆的性质不会变?会不会对其它节点造成影响导致这个二叉树不满足堆的性质?答案是不会。点蓝色注脚2看解释2)
-
插入节点80
-
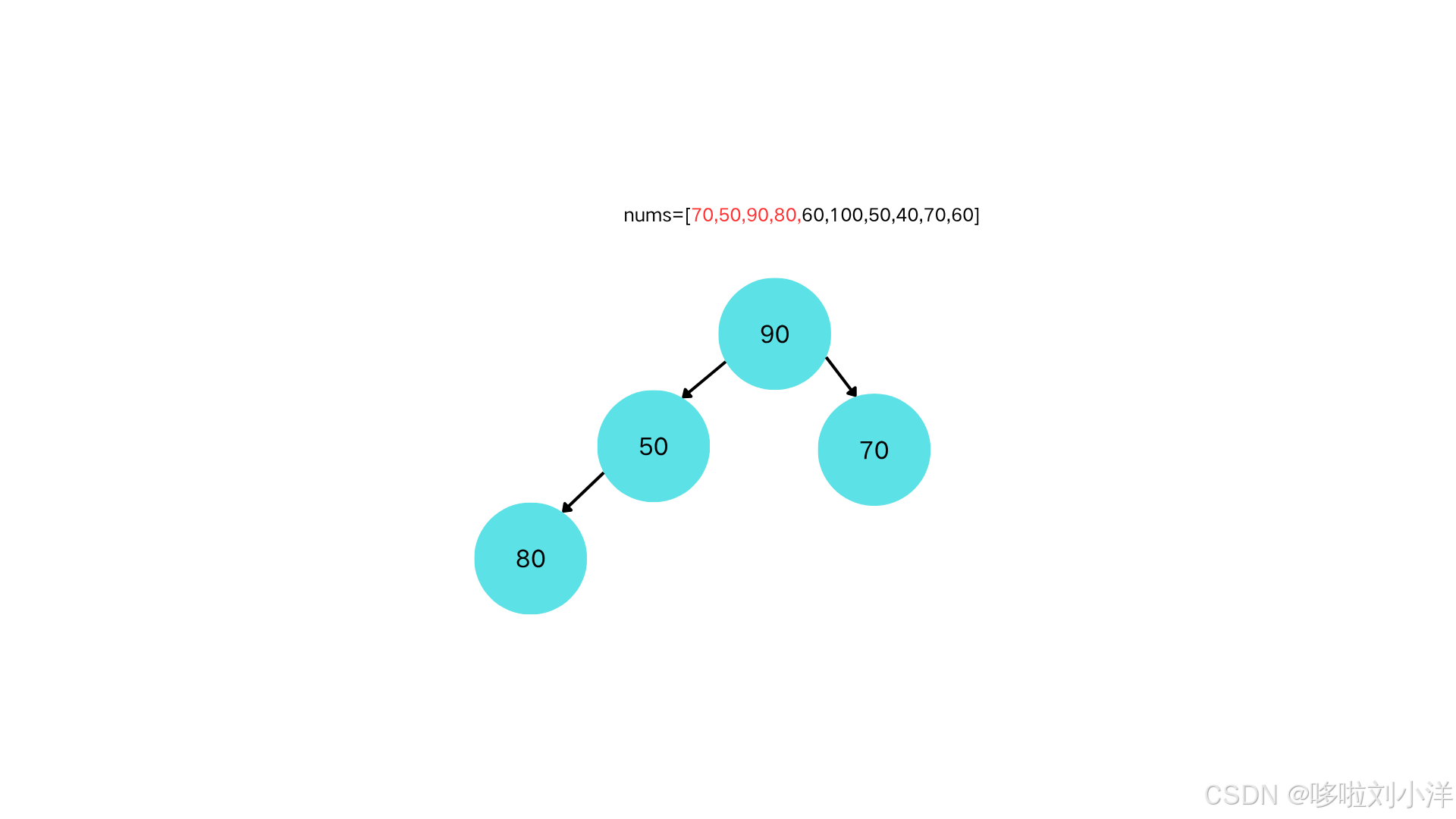
-
节点80和父节点50对比,需要"上浮"。交换(80,50)
-
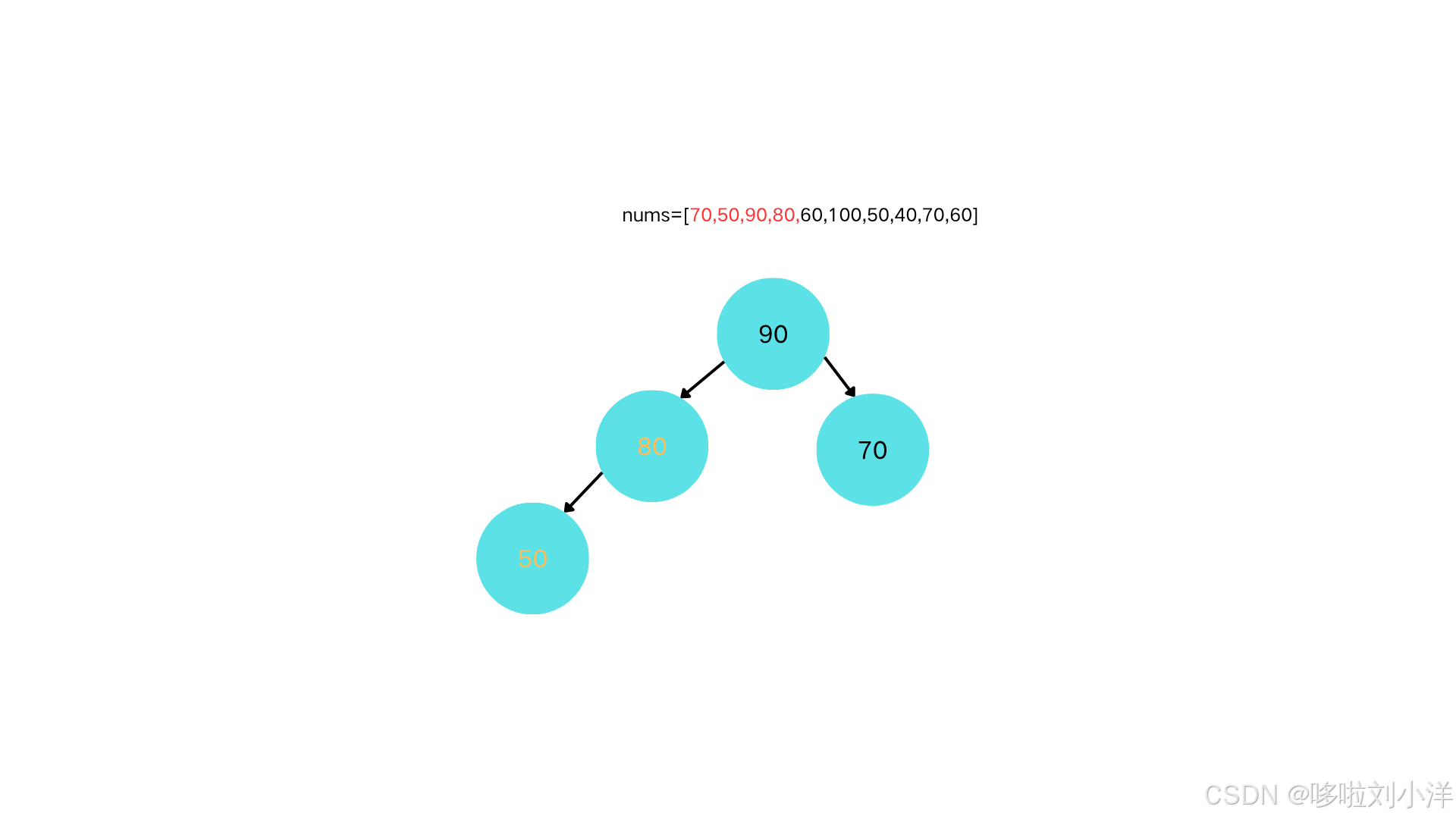
-
80的父节点90大于80,因此不需要继续上浮。
-
插入节点60
-
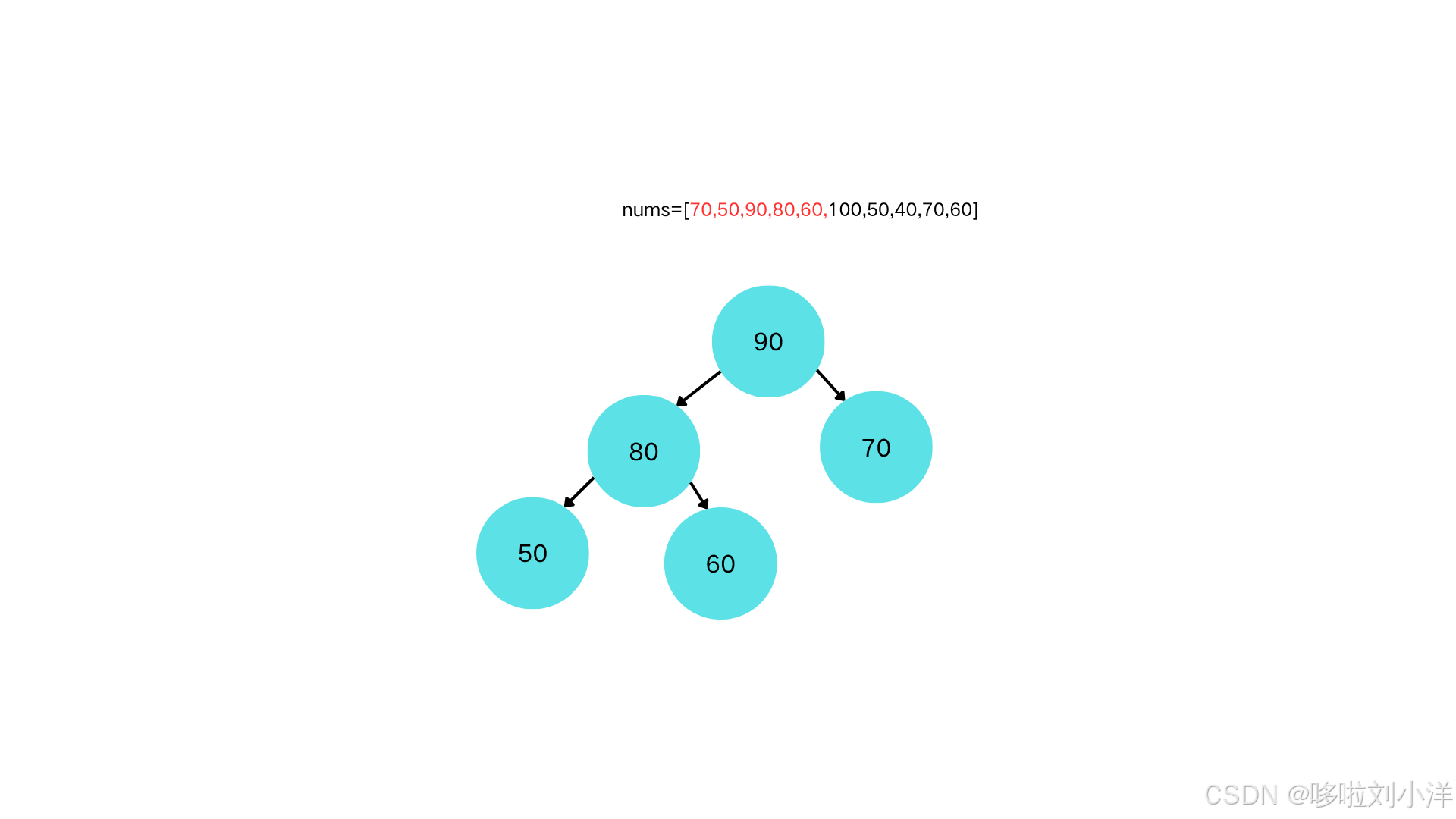
-
节点60和父节点80对比,不需要上浮
-
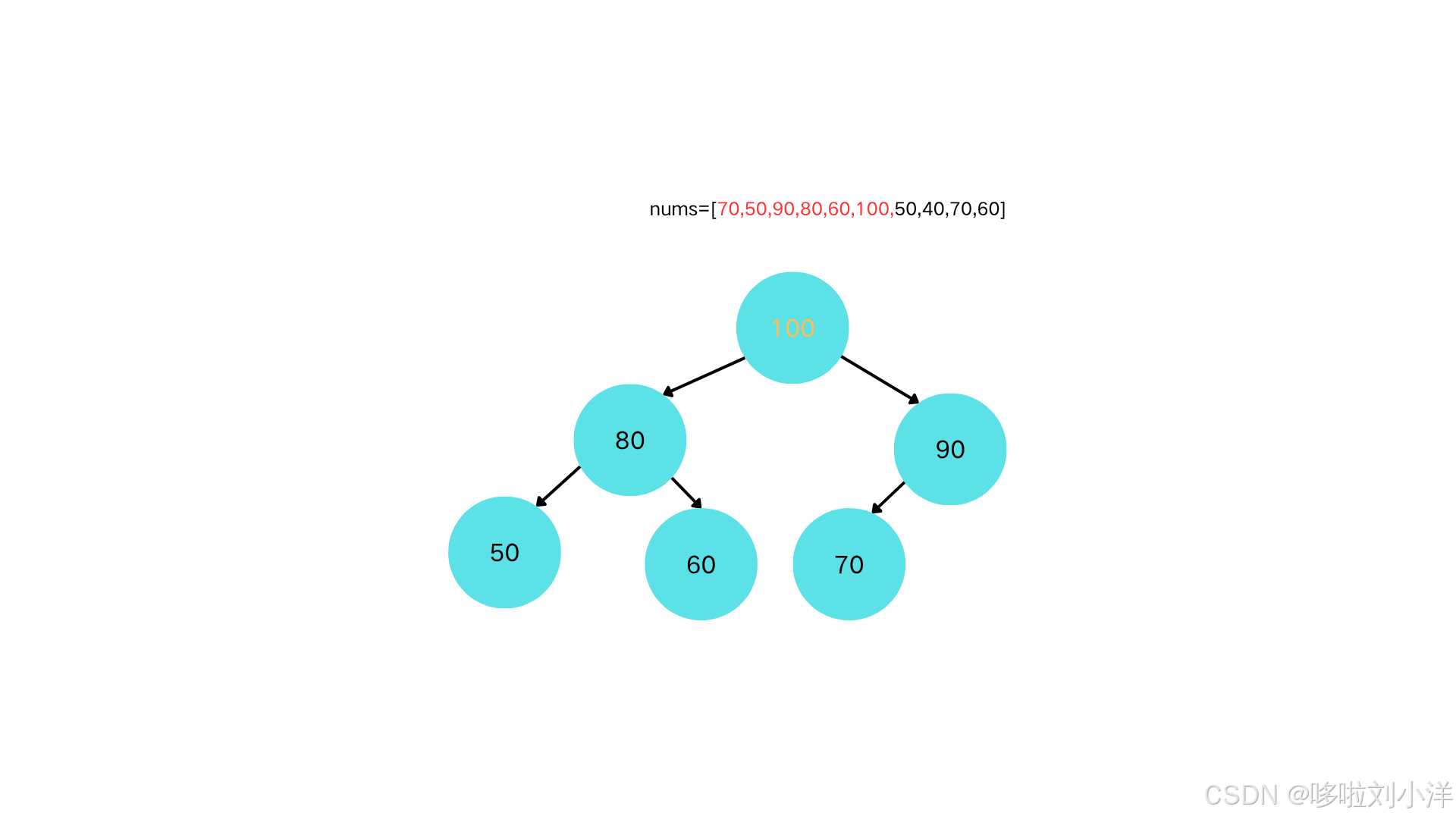
插入节点100
-
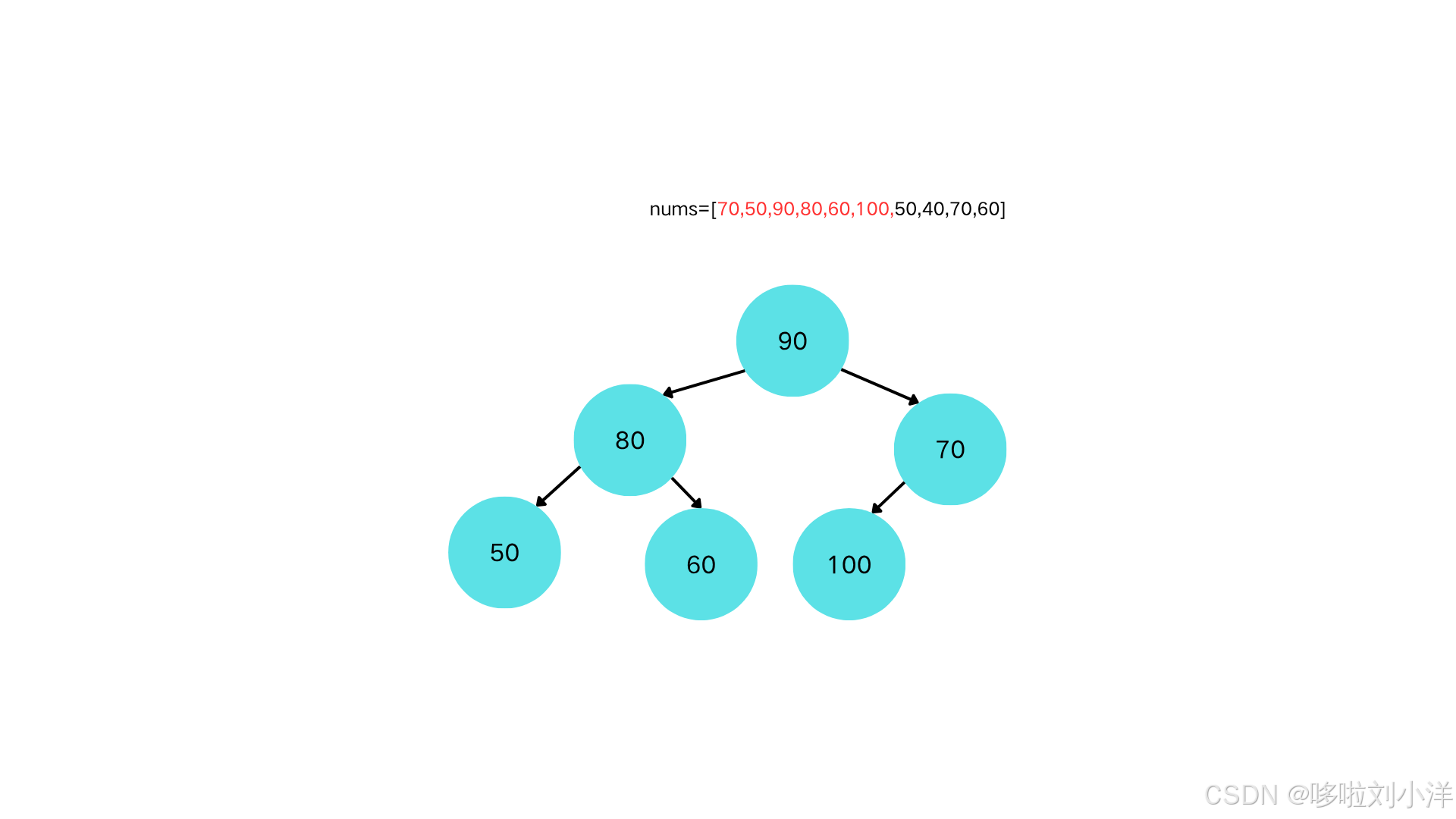
-
100>70,上浮。100>90,上浮
-
-
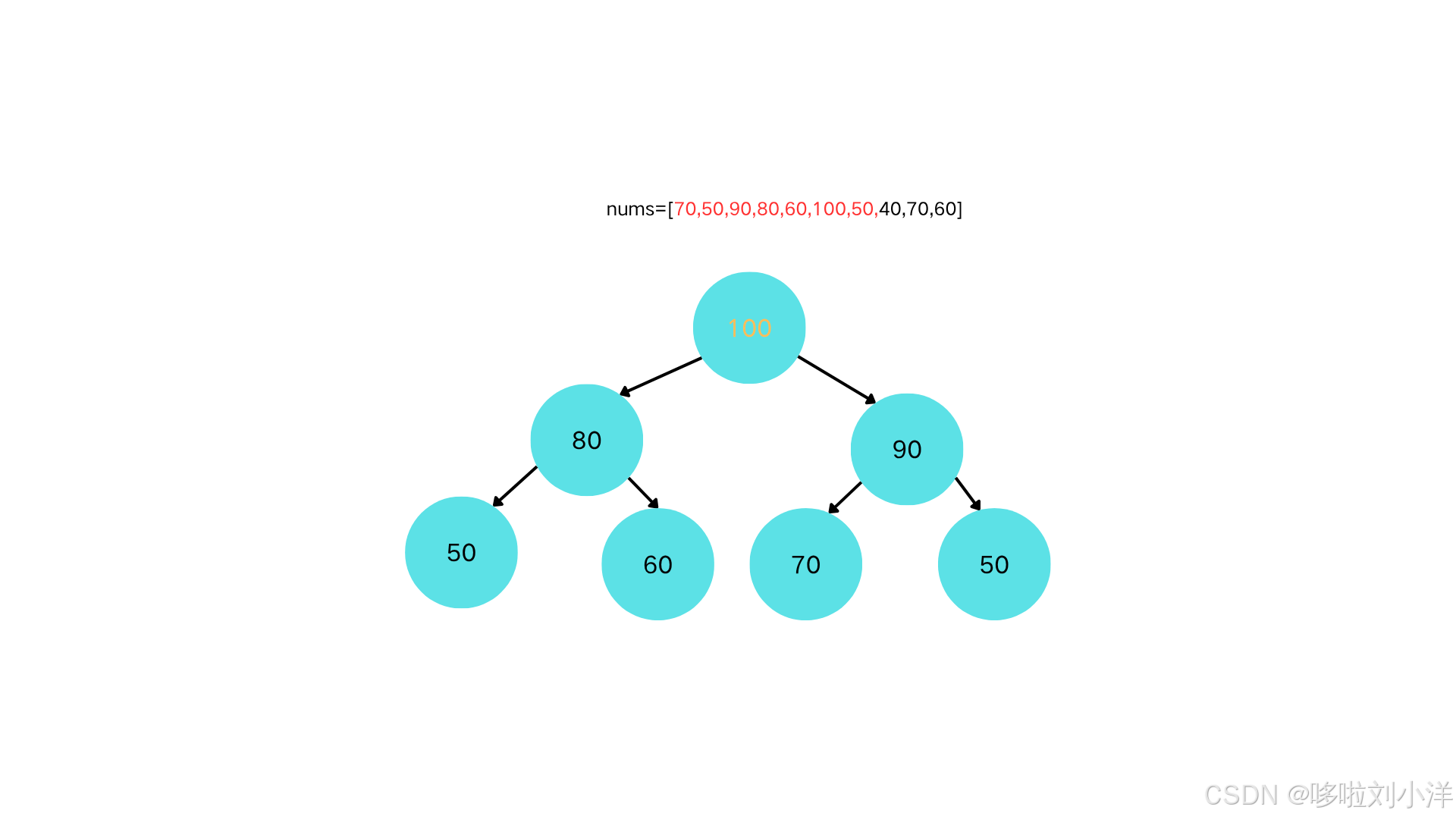
插入节点50
-
-
50<90,不需要上浮
-
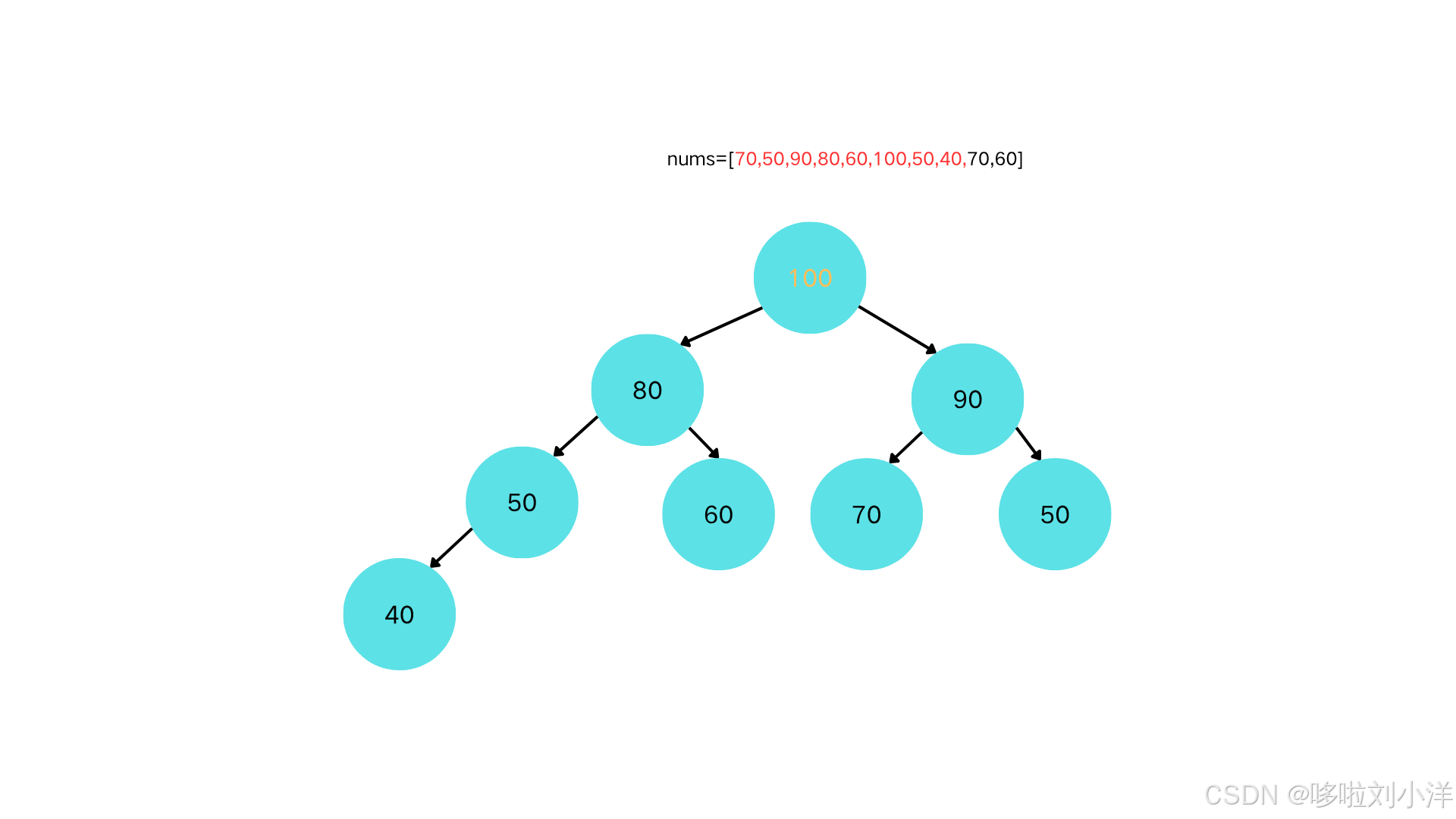
插入节点40
-
-
40<50,不需要上浮
-
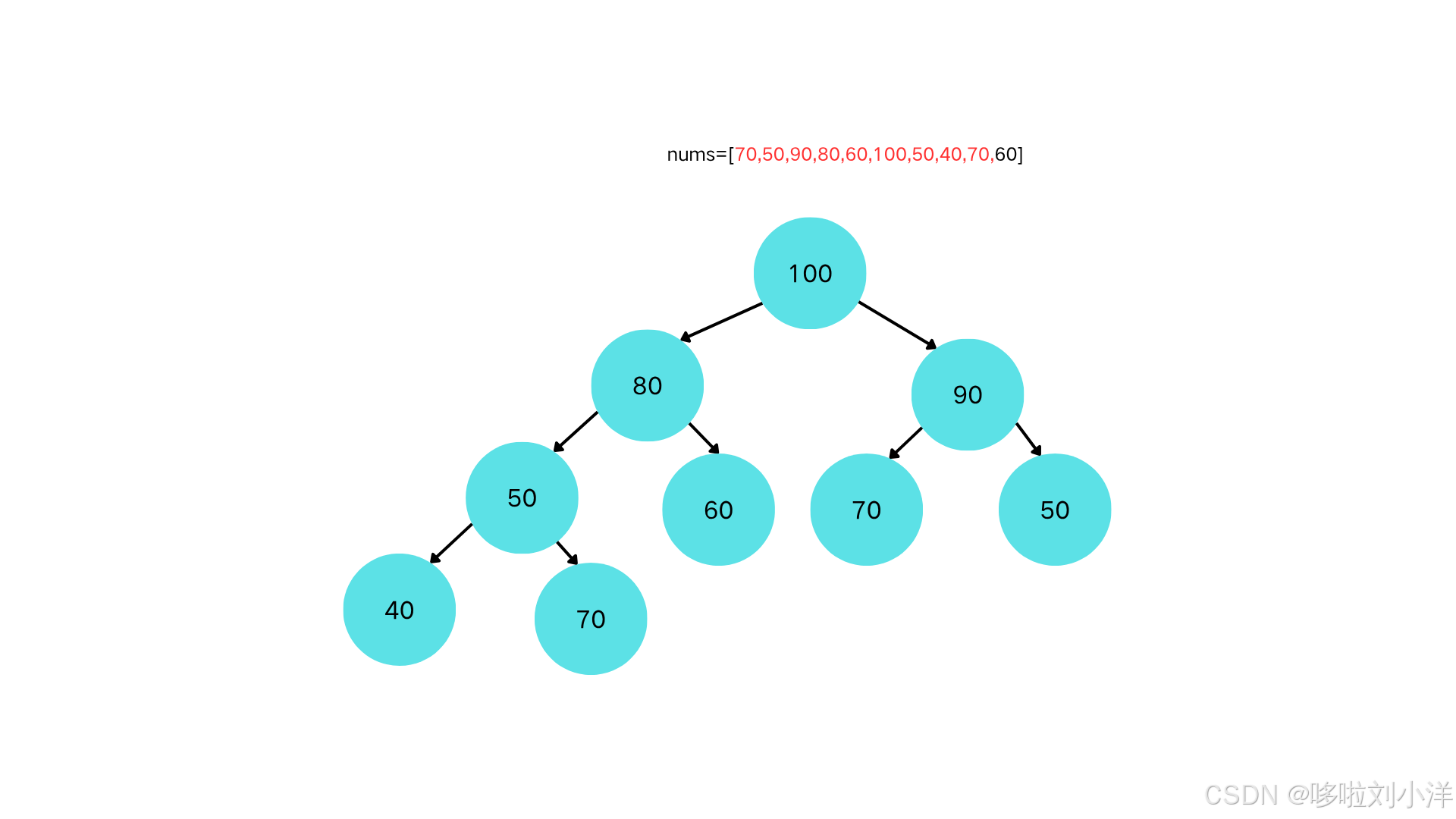
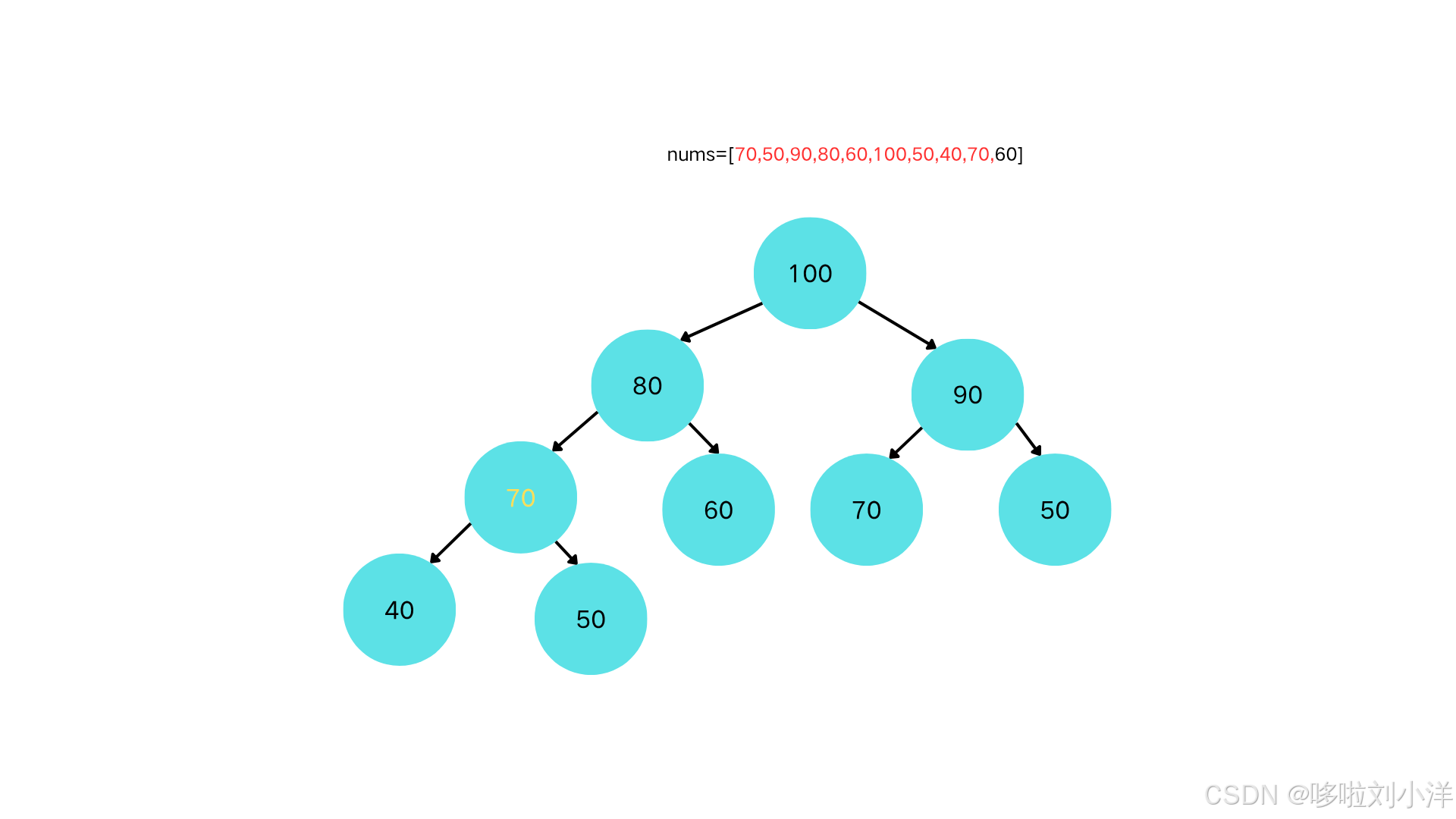
插入节点70
-
-
70>50,上浮。70<80,不上浮
-
-
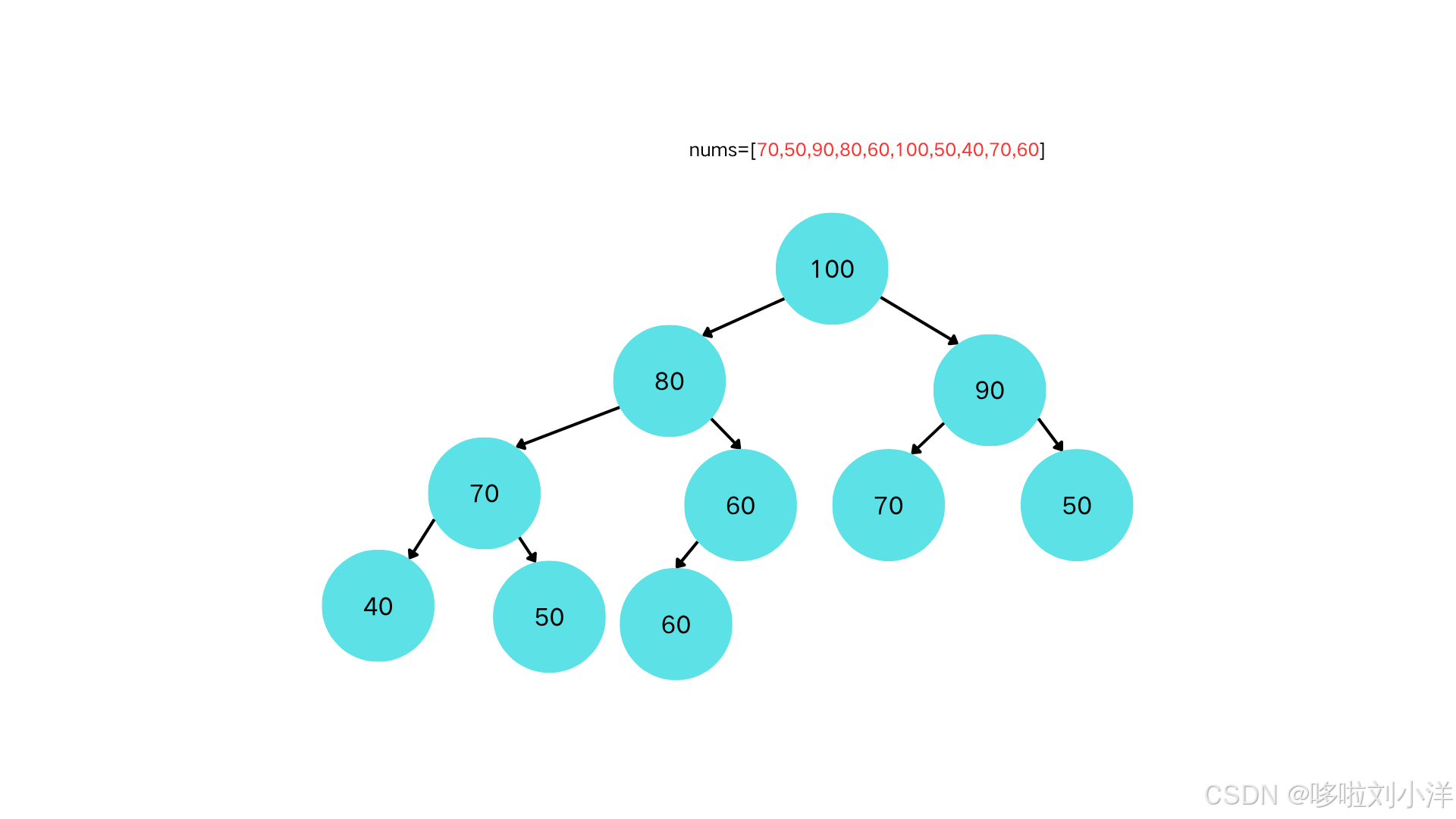
插入最后一个节点60
-
-
60==60,不需要上浮
到此,堆建立完毕。和一开始的堆图例做对比:
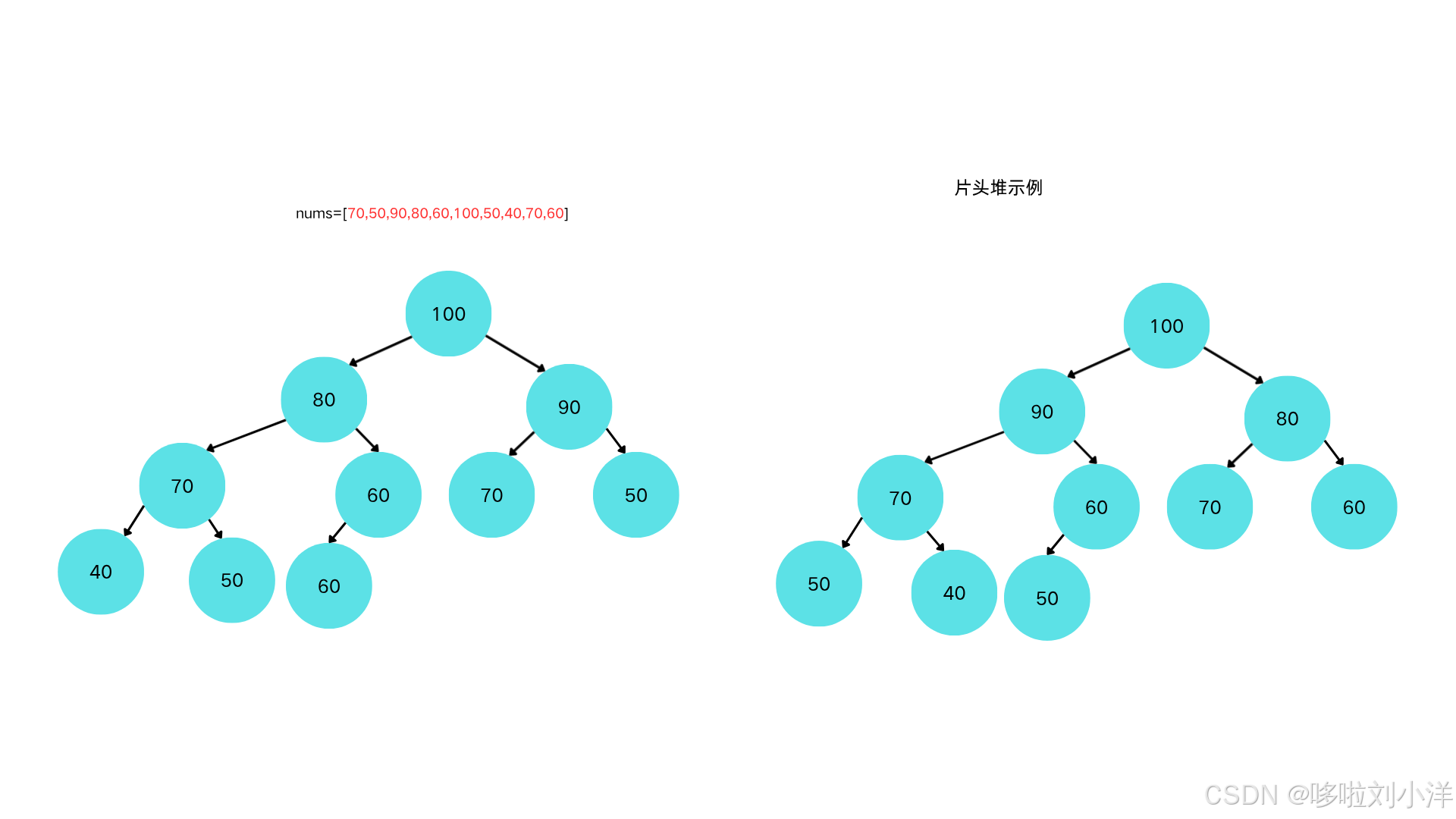
这里发现虽然两个二叉树节点对应位置不一样,但是都符号大根堆的性质。因此得出一个结论,数组打乱后构建成的堆是不一样的,但是性质一样。
由此总结:(大根堆为例)
1.插入元素:插入到堆末尾,严格来说是完全二叉树的末尾
2.更新操作:插入元素和其父节点比较,如果大于父节点,交换两个元素值。然后新父节点继续和其父节点比较,,依此类推
3.同样的数据,打乱顺序构建成不同的数组,构建出来的堆是不一样的,但是性质仍然一样。满足父节点>=子节点
.构建堆的代码
模拟图示过程,先新建立一个数组heap,然后顺序遍历nums数组,分别把元素加入heap。每次加入元素后,进行更新操作,即"上浮"操作
这个算法的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)
其本质是上浮操作
时间复杂度证明:
T ( n ) = ∑ k = 1 n ⌊ log 2 k ⌋ T(n) = \sum_{k=1}^{n} \lfloor \log_{2} k \rfloor T(n)=k=1∑n⌊log2k⌋
n是节点的个数。即每个节点最多上浮 l o g 2 k log_2k log2k次,比如 k=4,第4个节点在第三层,那么最多上浮两次。
⌊ x ⌋ \lfloor x\rfloor ⌊x⌋表示对x向下取整。所以有 T ( n ) = ∑ k = 1 n ⌊ log 2 k ⌋ < = ∑ k = 1 n log 2 k T(n)=\sum_{k=1}^{n} \lfloor \log_{2} k \rfloor<=\sum_{k=1}^{n} \log_2k T(n)=k=1∑n⌊log2k⌋<=k=1∑nlog2k
将求和公式展开,得到:
∑ k = 1 n log 2 k = log 2 1 + log 2 2 + . . . + log 2 ( n − 1 ) + log 2 n = log 2 ( 1 ∗ 2 ∗ 3 ∗ . . . ∗ n − 1 ∗ n ) \sum_{k=1}^{n}\log_2^k=\log_21+\log_22+...+\log_2(n-1)+\log_2n=\log_2{(1*2*3*...*n-1*n)} k=1∑nlog2k=log21+log22+...+log2(n−1)+log2n=log2(1∗2∗3∗...∗n−1∗n)
log 2 ( 1 ∗ 2 ∗ 3 ∗ . . . ∗ n ) = log 2 n ! \log_2{(1*2*3*...*n})=\log_2{n!} log2(1∗2∗3∗...∗n)=log2n!
根据斯特林公式
n ! ≈ 2 π n ( n e ) n n! \approx \sqrt{2\pi n} \left( \frac{n}{e} \right)^n n!≈2πn (en)n
得到:
log 2 n ! ≈ log 2 2 π n ( n e ) n = 1 2 log 2 ( 2 π n ) + n log 2 n − n log 2 e \log_2{n!} \approx\log_2{\sqrt{2\pi n} \left(\frac{n}{e} \right)^n}=\frac{1}{2}\log_2{(2 \pi n)}+n\log_2{n}-n\log_2{e} log2n!≈log22πn (en)n=21log2(2πn)+nlog2n−nlog2e
当 n 足够大的时候, n log 2 n 占据主导大小,换句话说,只需要考虑它即可 当n足够大的时候,n\log_2{n}占据主导大小,换句话说,只需要考虑它即可 当n足够大的时候,nlog2n占据主导大小,换句话说,只需要考虑它即可
因此,时间复杂度是 n log 2 n n\log_2n nlog2n
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 插入元素到堆中(下标从1开始),并执行上浮调整维持大根堆
void heapInsert(vector<int>& heap, int val)
{
// 插入到堆的末尾(下标为当前堆大小,因为从1开始)
heap.push_back(val);
int i = heap.size() - 1; // 当前元素的下标(刚插入的位置)
// 上浮操作:与父节点比较,若当前元素更大则交换
// 父节点下标为 i/2(整数除法),根节点下标为1,i>1时才需要调整
while (i > 1)
{
int parent = i / 2; // 父节点下标
if (heap[i] <= heap[parent])
{
break; // 满足大根堆性质,停止上浮
}
swap(heap[i], heap[parent]); // 交换当前节点与父节点
i = parent; // 继续向上调整
}
}
// 非原地构建大根堆(新建堆数组,下标从1开始)
vector<int> buildMaxHeap(const vector<int>& nums)
{
vector<int> heap;
heap.reserve(nums.size() + 1); // 预留空间,下标0闲置
heap.push_back(0); // 占位,使堆从下标1开始
// 逐个插入元素并调整堆
for (int num : nums)
{
heapInsert(heap, num);
}
return heap;
}
// 打印堆(从下标1开始)
void printHeap(const vector<int>& heap)
{
// 堆从下标1开始,到heap.size()-1结束
for (int i = 1; i < heap.size(); ++i)
{
cout << heap[i] << " ";
}
cout << endl;
}
int main()
{
// 原始数组
vector<int> nums = {70, 50, 90, 80, 60, 100, 50, 40, 70, 60};
cout << "原始数组: ";
for (int num : nums)
{
cout << num << " ";
}
cout << endl;
// 构建大根堆(非原地,下标从1开始)
vector<int> heap = buildMaxHeap(nums);
cout << "构建的大根堆(下标从1开始): ";
printHeap(heap);
return 0;
}
还有一种原地修改的算法,时间复杂度是 O ( n ) O(n) O(n)
其本质是下沉操作
时间复杂度证明:
1.有n个节点,完全二叉树的高度是: h = ⌊ l o g 2 n ⌋ h = ⌊log₂n⌋ h=⌊log2n⌋
2.第 i 层的节点数为 2 i 2^i 2i(i>=0)
3.每个节点的下沉操作次数最多为其 "到叶子的最大距离",即h - i(第i层节点最多下沉h - i层)。
因此,将每个节点下沉的次数之和加起来:(假设二叉树是满二叉树)
T ( n ) = ∑ i = 0 h − 1 2 i × ( h − i ) T(n) = \sum_{i=0}^{h-1} 2^i \times (h - i) T(n)=i=0∑h−12i×(h−i)
设 k = h − i k=h-i k=h−i,则有 i = h − k i=h-k i=h−k,确定上下界,当i=0的时候,k=h,当i=h-1的时候,k=1,所以
T ( n ) = ∑ k = 1 h 2 h − k × ( k ) T(n) = \sum_{k=1}^{h} 2^{h-k} \times (k) T(n)=k=1∑h2h−k×(k)
T ( n ) = 2 h − 1 ∗ 1 + 2 h − 2 ∗ 2 + 2 h − 3 ∗ 3 + . . . + 2 0 ∗ h T(n)=2^{h-1}*1+2^{h-2}*2+2^{h-3}*3+...+2^0*h T(n)=2h−1∗1+2h−2∗2+2h−3∗3+...+20∗h
2 ∗ T ( n ) = 2 h ∗ 1 + 2 h − 1 ∗ 2 + 2 h − 2 ∗ 3 + . . . + 2 2 ∗ ( h − 1 ) + 2 1 ∗ h 2 *T(n)=2^h*1+2^{h-1}*2+2^{h-2}*3+...+2^2*(h-1)+2^1*h 2∗T(n)=2h∗1+2h−1∗2+2h−2∗3+...+22∗(h−1)+21∗h
错位相减
T ( n ) = 2 h + 2 h − 1 + 2 h − 2 + ⋯ + 2 1 − h × 2 0 T(n) = 2^h + 2^{h-1} + 2^{h-2} + \dots + 2^1 - h \times 2^0 T(n)=2h+2h−1+2h−2+⋯+21−h×20
发现这是一个等比数列,用等比数列公式计算得出: T ( n ) = ( 2 h + 1 − 2 ) − h T(n)=(2 ^{h+1} −2)−h T(n)=(2h+1−2)−h
又因为树节点和高度的关系是: n = 2 h + 1 − 1 n=2^{h+1}-1 n=2h+1−1
2 h + 1 = n + 1 2^{h+1}=n+1 2h+1=n+1
关联得: T ( n ) = ( n − 1 ) − h ≈ n T(n)=(n-1)-h\approx n T(n)=(n−1)−h≈n
因此时间复杂度是 O ( log 2 n ) O(\log_2n) O(log2n)
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 下沉调整:确保以i为根的子树满足大根堆性质(下标从1开始)
void heapify(vector<int>& arr, int n, int i)
{
while (true)
{
int largest = i; // 当前节点(初始化为最大值位置)
int left = 2 * i; // 左子节点下标(1-based)
int right = 2 * i + 1; // 右子节点下标(1-based)
// 找到当前节点、左子节点、右子节点中的最大值
if (left <= n && arr[left] > arr[largest])
{
largest = left;
}
if (right <= n && arr[right] > arr[largest])
{
largest = right;
}
// 若最大值就是当前节点,无需继续调整
if (largest == i)
{
break;
}
// 交换当前节点与最大值节点,继续下沉
swap(arr[i], arr[largest]);
i = largest; // 下沉到子节点位置
}
}
// 原地构建大根堆(直接修改原始数组,下标从1开始)
void buildMaxHeapInPlace(vector<int>& arr)
{
int n = arr.size() - 1; // 有效元素数量(arr[0]闲置,实际元素从1到n)
// 从最后一个非叶子节点开始,向前逐个调整
// 最后一个非叶子节点下标为 n/2(1-based)
for (int i = n / 2; i >= 1; --i)
{
heapify(arr, n, i);
}
}
// 打印堆(从下标1开始)
void printHeap(const vector<int>& arr)
{
for (int i = 1; i < arr.size(); ++i)
{
cout << arr[i] << " ";
}
cout << endl;
}
int main() {
// 原始数据(为适配1-based,arr[0]闲置,有效元素从arr[1]开始)
vector<int> arr = {0, 70, 50, 90, 80, 60, 100, 50, 40, 70, 60};
// 注:arr[0]是占位符,实际元素为下标1~10的10个数据
cout << "原始数组(1-based): ";
printHeap(arr);
// 原地构建大根堆
buildMaxHeapInPlace(arr);
cout << "原地构建后的大根堆(1-based): ";
printHeap(arr);
return 0;
}.堆的删除操作
首先要理解下沉操作,上面代码详细说明了下沉得步骤。然后删除就非常简单。
将堆顶元素(删除元素)和堆最后一个元素交换,堆内元素计数器-1,然后对堆顶元素进行下沉操作。
cpp
void deleteHeapTop(vector<int>& arr, int& n)
{
if (n == 0)
{
cout << "堆为空,无法删除元素!" << endl;
return;
}
// 步骤1:将堆顶元素(下标1)与最后一个元素(下标n)交换
swap(arr[1], arr[n]);
// 步骤2:删除最后一个元素(原堆顶),堆大小减1
n--;
// 步骤3:对新的堆顶元素(原最后一个元素)执行下沉调整,恢复堆性质
if (n > 0)
{ // 若堆不为空,才需要调整
heapify(arr, n, 1);
}
}至此,堆的基本概念就说明完毕。大根堆和小根堆的逻辑类似。