深度学习算法学习（一）：梯度下降法和最简单的深度学习核心原理代码

梯度下降法

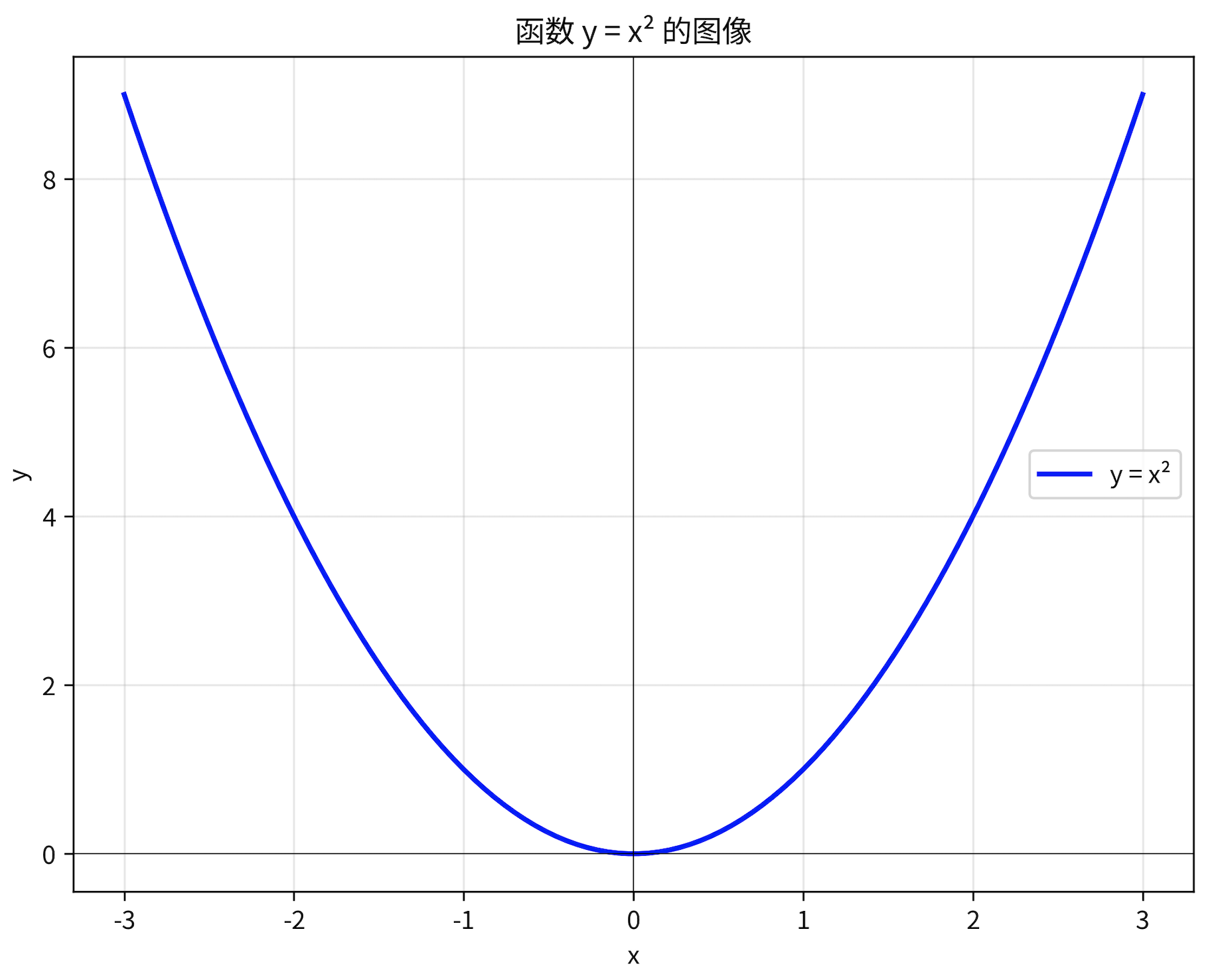
梯度下降法就是找函数最小值的方法，比方说这个函数

原函数为 y = x^2 导函数为 y = 2 * x

在x = -1 这个点，导数值为 -2

该点导数为负数 ，说明在这一点，如果x增大，y会减小

所以**f(x)**最小值的点应当在-1的右侧（大于-1）

梯度：可以理解为多元函数的导数，意义与导数基本一致

梯度下降公式

根据梯度，更新权重

学习率控制权重更新的幅度

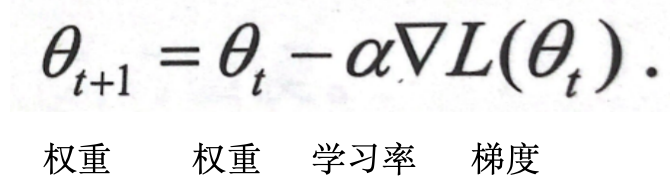
比方说上面，原函数为 y = x^2 导函数为 y = 2 * x

在 x = -1 这个点，导数值为 -2 ，假设我的学习率为 0.5，那么这个公式就为

权重 = -1 - (0.5 * -2) = 0

x = 0，对于y = x^2来讲就是这个函数的最小值

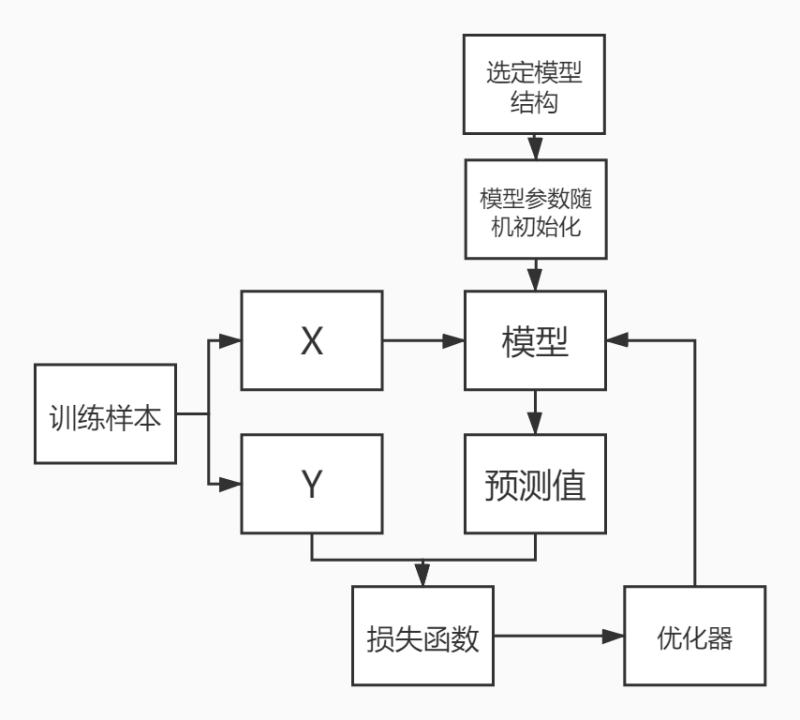
流程

1、选定模型结构
2、随机初始化模型参数
3、设置学习率
4、选定损失函数(均方差-两数相减求平方)

代码

python 复制代码

# X = [0.01 * x for x in range(100)]
# Y = [2*x**2 + 3*x + 4 for x in X]

# 训练样本
X = [0.0, 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.18, 0.19, 0.2, 0.21, 0.22, 0.23, 0.24, 0.25, 0.26, 0.27, 0.28, 0.29, 0.3, 0.31, 0.32, 0.33, 0.34, 0.35000000000000003, 0.36, 0.37, 0.38, 0.39, 0.4, 0.41000000000000003, 0.42, 0.43, 0.44, 0.45, 0.46, 0.47000000000000003, 0.48, 0.49, 0.5, 0.51, 0.52, 0.53, 0.54, 0.55, 0.56, 0.5700000000000001, 0.58, 0.59, 0.6, 0.61, 0.62, 0.63, 0.64, 0.65, 0.66, 0.67, 0.68, 0.6900000000000001, 0.7000000000000001, 0.71, 0.72, 0.73, 0.74, 0.75, 0.76, 0.77, 0.78, 0.79, 0.8, 0.81, 0.8200000000000001, 0.8300000000000001, 0.84, 0.85,
0.86, 0.87, 0.88, 0.89, 0.9, 0.91, 0.92, 0.93, 0.9400000000000001, 0.9500000000000001, 0.96, 0.97, 0.98, 0.99]
Y = [4.0, 4.0302, 4.0608, 4.0918, 4.1232, 4.155, 4.1872, 4.2198, 4.2528, 4.2862, 4.32, 4.3542, 4.3888, 4.4238, 4.4592, 4.495, 4.5312, 4.5678, 4.6048, 4.6422, 4.68, 4.7181999999999995, 4.7568, 4.7958, 4.8352, 4.875, 4.9152000000000005, 4.9558, 4.9968, 5.0382, 5.08, 5.122199999999999, 5.1648, 5.2078, 5.2512, 5.295, 5.3392, 5.3838, 5.4288, 5.4742, 5.5200000000000005, 5.5662, 5.6128, 5.6598, 5.7072, 5.755, 5.8032, 5.851800000000001, 5.9008, 5.9502, 6.0, 6.0502, 6.1008, 6.1518, 6.203200000000001, 6.255000000000001, 6.3072, 6.3598, 6.4128, 6.4662, 6.52, 6.5742, 6.6288, 6.6838, 6.7392, 6.795, 6.8512, 6.9078, 6.9648, 7.022200000000001, 7.08, 7.138199999999999, 7.1968, 7.2558, 7.3152, 7.375, 7.4352, 7.4958, 7.5568, 7.6182, 7.680000000000001, 7.7422, 7.8048, 7.867800000000001, 7.9312, 7.994999999999999, 8.0592, 8.1238, 8.1888, 8.2542, 8.32, 8.3862, 8.4528, 8.5198, 8.587200000000001, 8.655000000000001, 8.7232, 8.7918, 8.8608, 8.9302]

# 1、选定模型结构
def func(x_true):
    y_predict = w1 * x_true**2 + w2 * x_true + w3
    return y_predict

# 2、 随机初始化模型参数
w1, w2, w3 = 1, 0, -1

# 3、设置学习率
lr = 0.1

# 4、选定损失函数(均方差-两数相减求平方)
def loss(y_predict, y_true):
    return (y_predict - y_true) ** 2

# 训练1000轮
for epoch in range(1000):
    epoch_loss = 0
    for x_true, y_true in zip(X, Y):
        # y的预测值
        y_predict = func(x_true)
        # 损失计算(将每个批次的损失值不断加到epoch_loss变量上)
        epoch_loss += loss(y_predict, y_true)
        # 梯度计算(每个常量参数对于loss函数求偏导,因为我们希望loss函数返回为0,也就是取损失函数的最小值)
        # 推导过程:
        # w1对于loss函数求偏导
        # 根据复合函数的链式求导规则,先对loss函数求导再对内层y_predict求导,然后乘积
        # ((y_predict - y_true) ** 2)' = 2 * (y_predict - y_true) * (y_predict)'
        # (y_predict)' = (w1 * x_true**2 + w2 * x_true + w3)'
        # 求w1的偏导数,对于w1来说 x_true**2 和 w2 * x_true + w3 视为常数
        # 所以w1的偏导数为x_true**2
        grad_w1 = 2 * (y_predict - y_true) * x_true ** 2
        grad_w2 = 2 * (y_predict - y_true) * x_true
        grad_w3 = 2 * (y_predict - y_true)
        # 权重更新
        w1 = w1 - lr * grad_w1   #sgd
        w2 = w2 - lr * grad_w2 
        w3 = w3 - lr * grad_w3

    # 计算平均损失
    epoch_loss /= len(X)
    print("第%d轮， loss %f" %(epoch, epoch_loss))
    if epoch_loss < 0.000000000001:
        break

print(f"训练后权重:w1:{w1} w2:{w2} w3:{w3}")

输出的权重，接近于生成样本的函数 Y=[2x**2 + 3x + 4 for x in X]

python 复制代码

训练后权重:w1:2.000018622086053 w2:2.999975670984378 w3:4.000005923313498