分类任务-三个重要网络模型

一、卷积过程参数计算

重要公式：O=(I-K+2P)/S + 1，O是输出尺寸，I是输入尺寸，K是卷积核尺寸，P是padding，S是步长，向下取整。

例1.特征图3*4*4，padding=1，卷积核数量是1，卷出来的特征图为1*4*4，问卷积核多大，卷积核的参数量是多少

分析：特征图是三通道，大小为4，根据重要公式，可以计算出卷积核的大小为3，又因为是在三通道上做卷积，故卷积核也是三通道的，所以卷积核是3*3*3的大小，参数量是27

例2.特征图3*4*4，卷积核3*3*3，padding=1，卷积核数量7，卷出来的特征图多大

分析：根据重要公式得，卷出来的特征图大小为4，又因为卷积核的数量为7，由于卷积核的数量等于输出特征图的数量。故卷出来的特征图大小为7*4*4

例三.特征图64*224*224，卷积核64*3*3，padding=1，卷积核数量128，卷出来特征图多大。这套卷积核的参数量是多少

分析：根据重要公式可以计算出卷出来的特征图尺寸大小为224，由于卷积核数量等于输出特征图的数量，故卷出来的特征图大小为128*224*224。这套卷积核的参数量是128*64*3*3

二、AlexNet实现

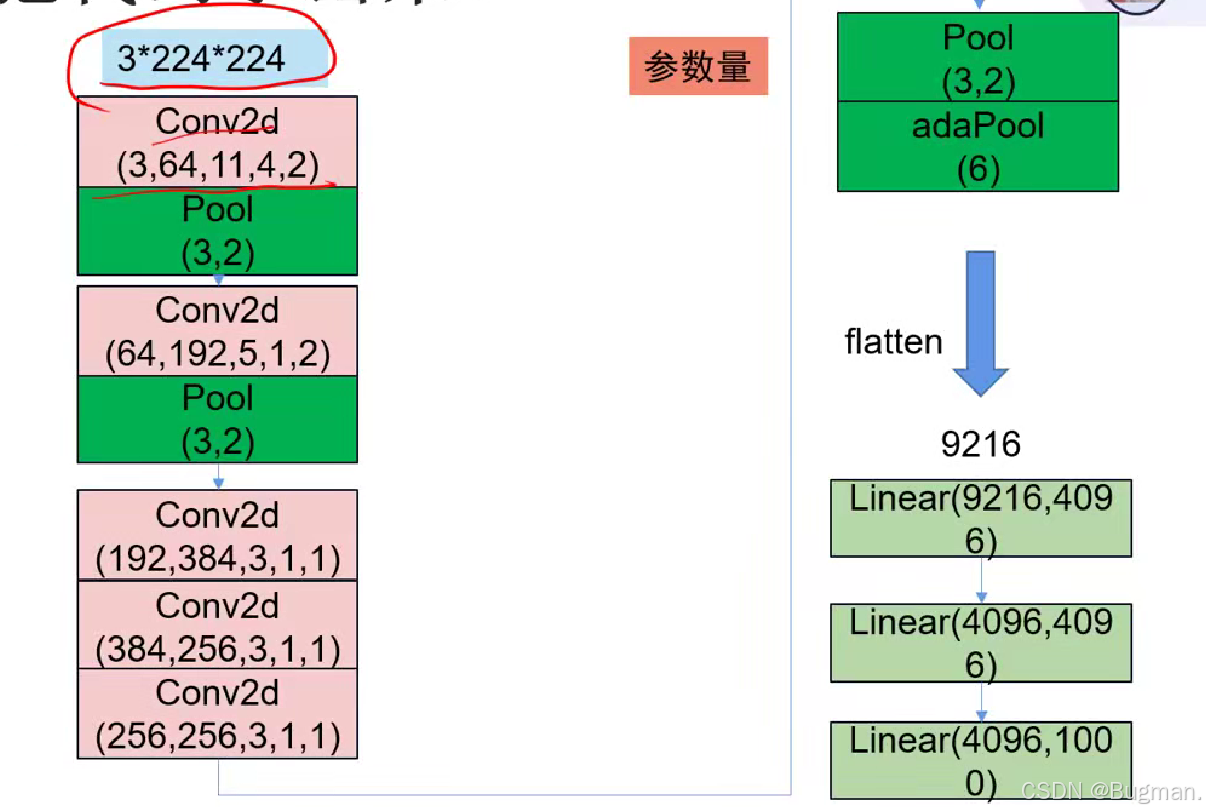
python 复制代码

import torch
from torch.nn import Sequential, Conv2d, MaxPool2d, AdaptiveMaxPool2d, Flatten, Linear


class MyAlexNet:
    def __init__(self, num_class):
        super(MyAlexNet, self).__init__()
        self.features = Sequential(
            Conv2d(3, 64, 11, 4, 2),
            MaxPool2d(3, 2),
            Conv2d(64, 192, 5, 1, 2),
            MaxPool2d(3, 2),
            Conv2d(192, 384, 3, 1, 1),
            Conv2d(384, 256, 3, 1, 1),
            Conv2d(256, 256, 3, 1, 1),
            MaxPool2d(3, 2)
        )
        self.classifier = Sequential(
            AdaptiveMaxPool2d(6),
            Flatten(),
            Linear(9216, 4096),
            Linear(4096, 4096),
            Linear(4096, num_class)
        )

    def forward(self, x):
        x = self.features(x)
        x = x.view(x.size(0), 9216)
        x = self.classifier(x)

三、VGGNet实现

VGGNet网络的特点是用小参数代替大参数，我们这里分析VGG网络每一层的参数量，并且实现网络

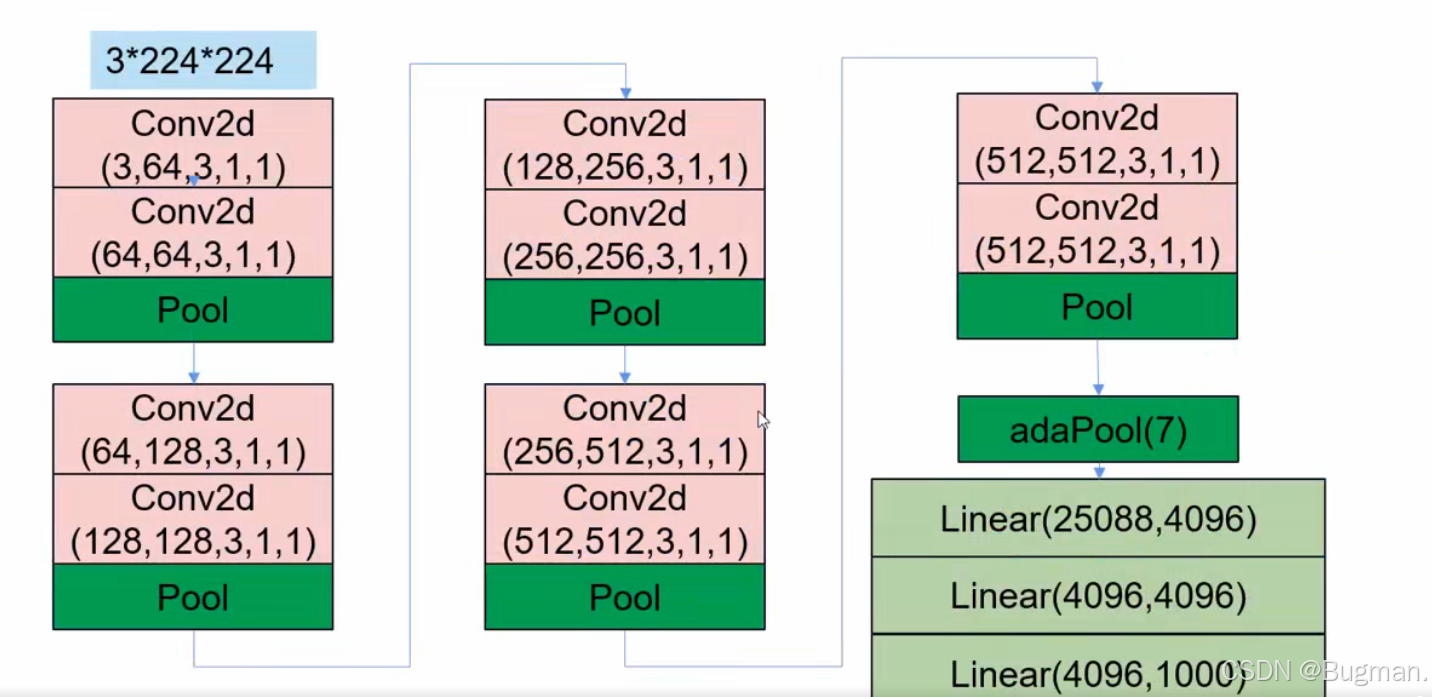
python 复制代码

import torch
from torch import nn
from torch.nn import Sequential, Conv2d, MaxPool2d, AdaptiveMaxPool2d, Flatten, Linear


class MyVGG(nn.Module):
    def __init__(self, num_class=1000):
        super(MyVGG, self).__init__()
        self.features = Sequential(
            # 输入3*224*224大小的特征图
            Conv2d(3, 64, 3, 1, 1),  # 参数量64*3*3*3+64 特征图大小为64*224*224
            # (+64是因为64个卷积核每一个都有一个偏置)
            Conv2d(64, 64, 3, 1, 1),  # 参数量64*64*3*3+64   特征图大小为64*224*224
            MaxPool2d(2),  # 特征图大小为64*112*112

            Conv2d(64, 128, 3, 1, 1),  # 参数量128*64*3*3+128 特征图大小为128*112*112
            Conv2d(128, 128, 3, 1, 1),  # 参数量 128*128*3*3+128 特征图大小为128*112*112
            MaxPool2d(2),  # 特征图大小为128*56*56

            Conv2d(128, 256, 3, 1, 1),  # 参数量256*128*3*3+256 特征图大小为256*56*56
            Conv2d(256, 256, 3, 1, 1),  # 参数量 256*256*3*3+256 特征图大小为256*56*56
            MaxPool2d(2),  # 特征图大小为256*28*28

            Conv2d(256, 512, 3, 1, 1),  # 参数量512*256*3*3+512 特征图大小为512*28*28
            Conv2d(512, 512, 3, 1, 1),  # 参数量 512*512*3*3+512 特征图大小为512*28*28
            MaxPool2d(2),  # 特征图大小为512*14*14

            Conv2d(512, 512, 3, 1, 1),  # 参数量512*512*3*3+512 特征图大小为512*14*14
            Conv2d(512, 512, 3, 1, 1),  # 参数量 512*512*3*3+512 特征图大小为512*14*14
            MaxPool2d(2),  # 特征图大小为512*7*7

            AdaptiveMaxPool2d(7)  # 自适应池化后，特征图大小为512*7*7
        )
        self.classifier = Sequential(
            Flatten(),
            Linear(512 * 7 * 7, 4096),
            Linear(4096, 4096),
            Linear(4096, num_class)
        )

    def forward(self, x):
        x = self.features(x)
        x = self.classifier(x)
        return x


def get_parameter_number(model):
    total_num = sum(p.numel() for p in model.parameters())
    trainable_num = sum(p.numel() for p in model.parameters() if p.requires_grad)
    return {'Total': total_num, 'Trainable': trainable_num}


# 测试模型
if __name__ == "__main__":
    model = MyVGG()
    params = get_parameter_number(model)
    print(f"总参数量: {params['Total']:,}")
    print(f"可训练参数量: {params['Trainable']:,}")

四、ResNet

ResNet 通过引入残差块 解决退化问题，其核心思想是：让网络学习残差（Residual）而非直接学习目标映射。

残差块结构

一个残差块包含：

主路径（Main Path）：由卷积层、BN 层、ReLU 激活组成的特征变换（记为 F(x)）。
跳跃连接（Skip Connection）：直接将输入 x 跳过主路径连接到输出（恒等映射，Identity Mapping）。

最终输出为：y=F(x)+x即网络只需学习 残差 F(x)=y−x，而非直接学习 y。