多策略改进蛇优化算法(ISO)的相关论文发表在期刊"Journal of Bionic Engineering"
01.引言
蛇优化器(SO)作为一种模拟蛇类交配行为的元启发式算法,近年来在全局数值优化和工程应用中展现出强大潜力。然而,其探索阶段的随机性缺陷与孵化过程的低效性,导致收敛速度慢、解质量受限。面对高维、非线性、多模态的现代工程难题,传统SO如同「盲眼巨蟒」------虽具力量,却失精准。
为此,提出多策略改进蛇优化器,通过三重创新突破SO的生物学局限:
- 多策略探索算子:融合随机搜索与定向开发,引入全局精英信息与对立种群交互
- 种群拥挤自适应孵化:基于维度级分布特征动态调整个体再生策略
- 序列二次规划局部搜索:嫁接数学优化利器,强化局部极值挖掘能力
02.算法原理简介及算法实现流程(文末附代码)
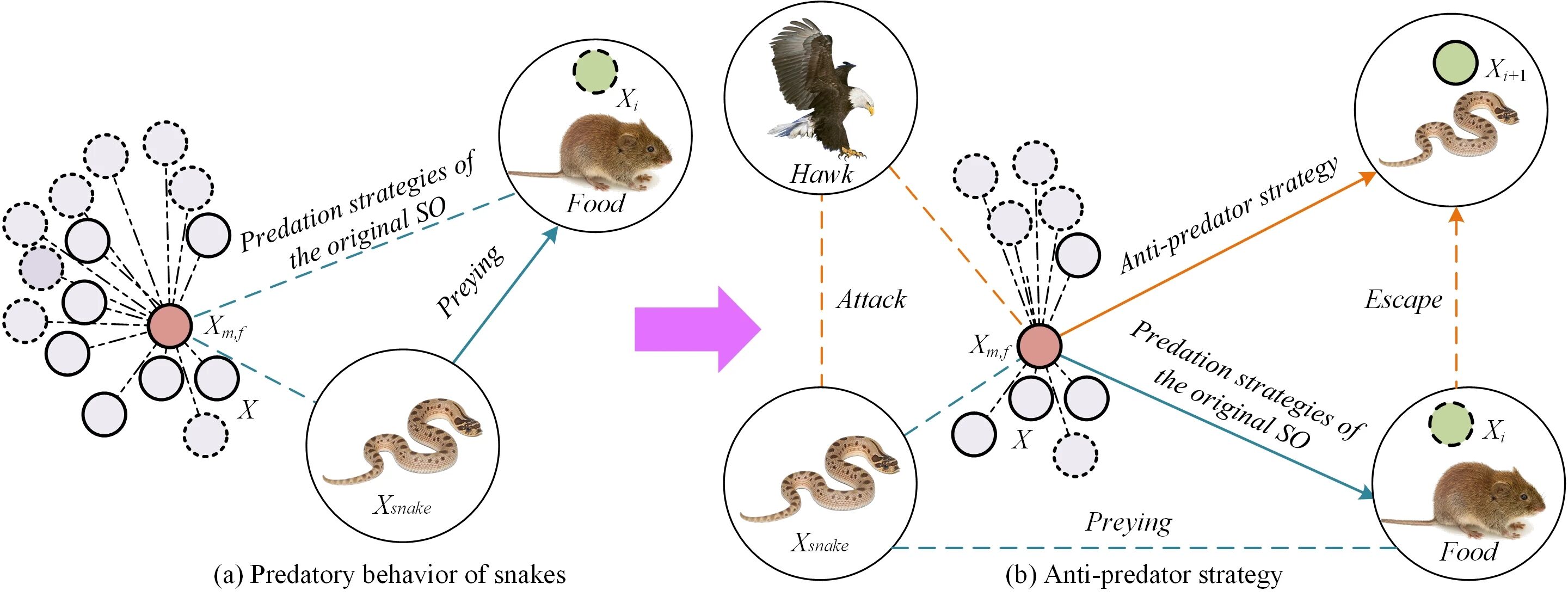
一、生物灵感与算法瓶颈
蛇优化器的核心灵感源于蛇类的温度驱动行为模式:
- 低温觅食(探索阶段):随机搜索食物源(全局空间)
- 高温趋食(开发阶段):向最优食物源移动(局部开发)
- 战斗/交配模式:个体竞争与基因重组
- 孵卵机制:劣解替换与种群更新
然而,SO存在两大本质缺陷:
- 探索阶段随机性过强:仅依赖当前子种群随机个体,忽视全局精英信息与对立种群交互,导致搜索方向盲目
- 孵卵过程低效:随机再生劣解个体,未考虑种群分布特征,浪费计算资源
二、MISO核心创新:三重策略融合
1. 多策略探索算子------【蛇群协同狩猎】
策略结构:
第一策略:保留原SO随机搜索(Eq.5-6)
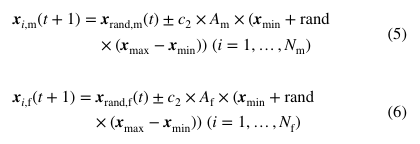
第二策略:当前个体邻域精细搜索(Eq.21-22)
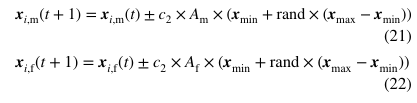
第三策略:改进型"current-to-pbest/1"策略(Eq.25-26)
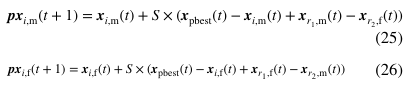
创新点:
- 引入全局精英个体(x_pbest)引导搜索方向
- 融合对立种群随机个体(x_rand,opposite)扩大搜索范围
- 通过竞争选择机制(Eq.27-28)保留最优候选解

**2. 种群拥挤自适应孵化------「智能蛋巢调控」**
种群拥挤度计算:
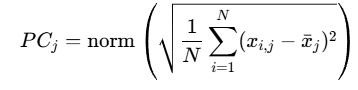
孵化策略切换:
高拥挤维度(PC_j > H):采用开发策略(Eq.32-33)
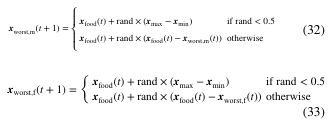
向最优个体靠拢(加速收敛)
向最差个体反向搜索(逃离局部极值)
低拥挤维度(PC_j ≤ H):采用探索策略(Eq.34-35)
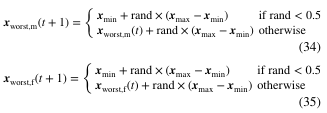
保守随机搜索(保持多样性)
最差个体信息利用(边界探索)
3. 序列二次规划局部搜索------「数学手术刀」
将非线性约束优化问题转化为二次规划子问题(Eq.39):
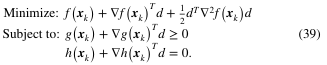
通过牛顿迭代步长调整,实现对最优解区域的精细挖掘

03.本文代码效果图
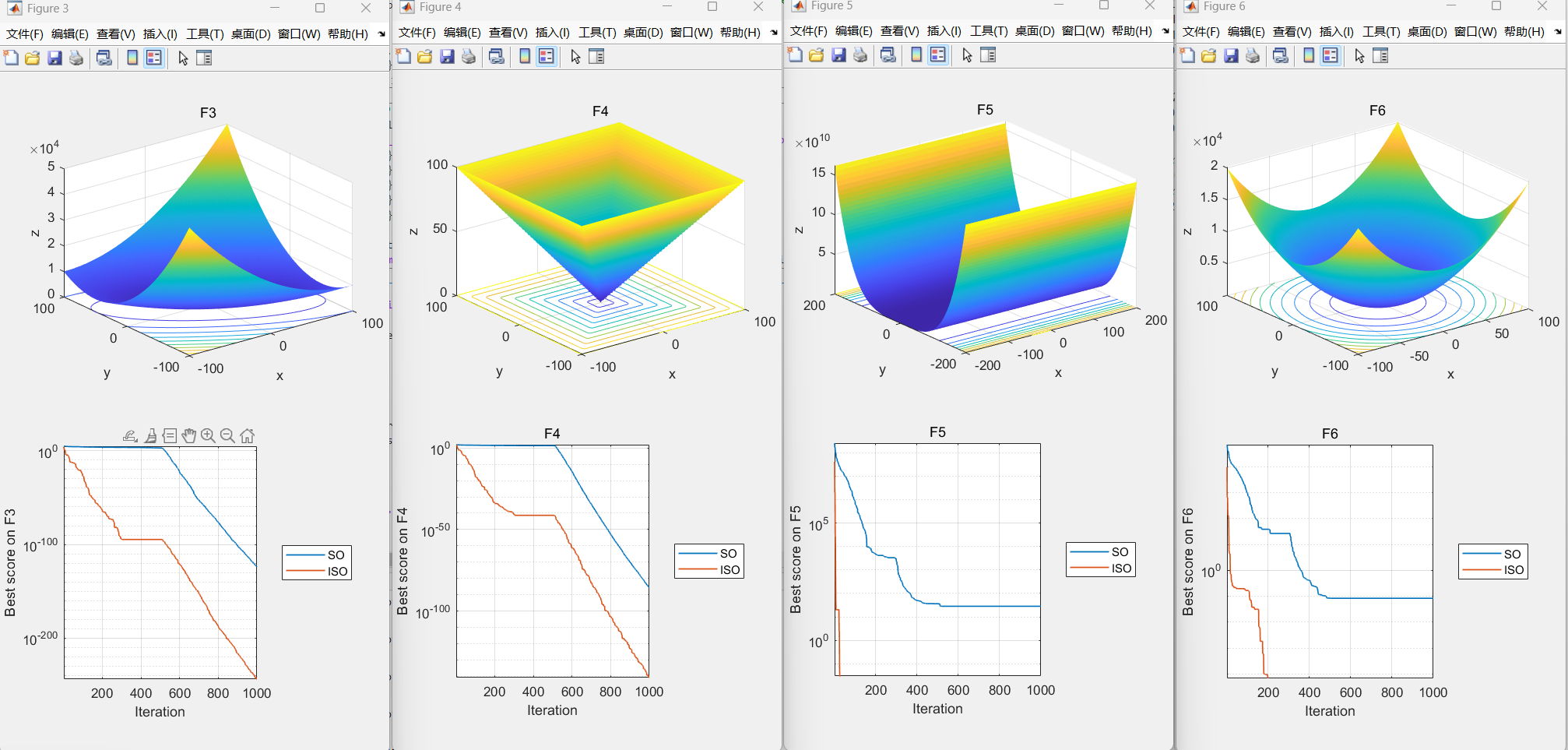
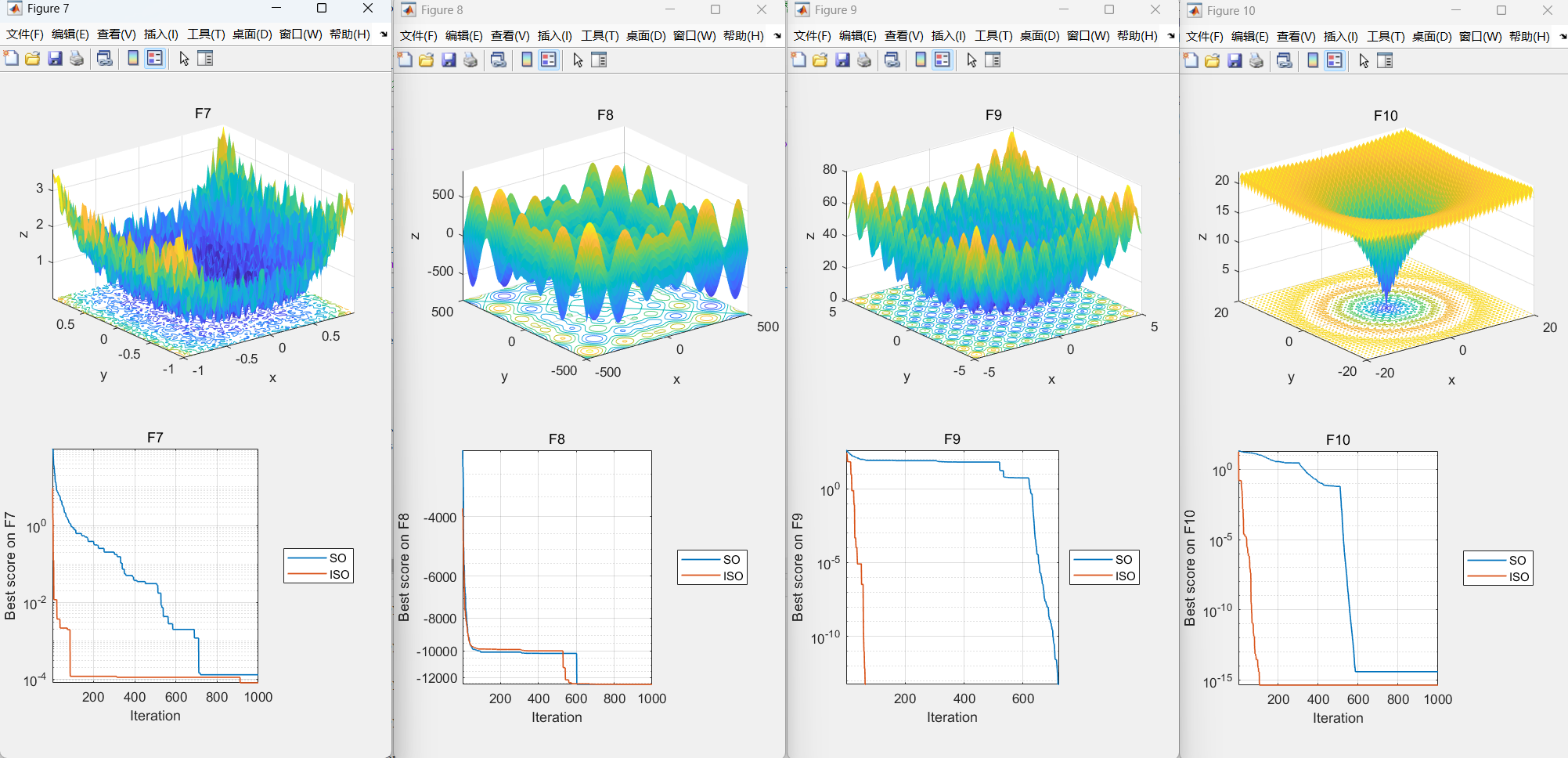
04.部分代码
function [ fval,Xfood,gbest_t] = ISO(N,T,lb,ub,dim,fobj)
%initial
vec_flag=[1,-1];
Threshold=0.25;
Thresold2= 0.6;
C1=0.5;
C2=.05;
C3=2;
% Strategy 1: Multi-strategy chaotic system(MSCS)
% % Initialization
if length(lb)<2
X=lb+MSCS(N,dim)*(ub-lb);
else
X=repmat(lb,N,1)+MSCS(N,dim).*repmat((ub-lb),N,1);%eq.(10)
end
for i=1:N
fitness(i)=fobj(X(i,:));
end
Trajectories=zeros(N,T);
position_history=zeros(N,T,dim);
fitness_history=zeros(N,T);
[GYbest, gbest] = min(fitness);
Xfood = X(gbest,:);
%Diving the swarm into two equal groups males and females
Nm=round(N/2);%eq.(1)
Nf=N-Nm;
Xm=X(1:Nm,:);
Xf=X(Nm+1:N,:);
fitness_m=fitness(1:Nm);
fitness_f=fitness(Nm+1:N);
[fitnessBest_m, gbest1] = min(fitness_m);
Xbest_m = Xm(gbest1,:);
[fitnessBest_f, gbest2] = min(fitness_f);
Xbest_f = Xf(gbest2,:);
for t = 1:T
Positions=[Xm;Xf];
for i=1:size(Positions,1)
position_history(i,t,:)=Positions(i,:);
Trajectories(:,t)=Positions(:,1);
fitness_history(i,t)=fobj(Positions(i,:));
end
Temp=exp(-((t)/T)); %eq.(2)
Q=C1*exp(((t-T)/(T)));%eq.(3)
if Q>1 Q=1; end
% Exploration Phase (no Food)
if Q<Threshold
for i=1:Nm
%Strategy 1: MSCS
lb_ap=lb(1)/t;
ub_ap=ub(1)/t;
z = rand(1, 1);
z = sin(pi*( z .* (1 - z)+ sin(pi * z))); %eq.(13)
for j=1:1:dim
rand_leader_index = floor(Nm*rand()+1);
X_randm = Xm(rand_leader_index, :);
flag_index = floor(2*rand()+1);
Flag=vec_flag(flag_index);
Am=exp(-fitness_m(rand_leader_index)/(fitness_m(i)+eps));
Xnewm1(i,j)=X_randm(j)+Flag*C2*Am*((ub(1)-lb(1))*rand+lb(1));%eq.(4)
end
% Strategy 2: Anti-predator strategies(APS-m)
Xnewm2(i,:)= X(i,:) -round(1+z).* (lb_ap+ rand(1,1) .* (ub_ap-lb_ap)); %eq.(16)
Xnewm2(i,:) = max(Xnewm2(i,:),lb_ap);Xnewm2(i,:) = min(Xnewm2(i,:),ub_ap);
if fobj(Xnewm2(i,:)) < fobj(Xnewm1(i,:))%eq.(17)
Xnewm(i,:)=Xnewm2(i,:);%eq.(17)
else
Xnewm(i,:)=Xnewm1(i,:);%eq.(17)
end
if(fobj(Xnewm(i,:))<fitness(i))%eq.(20)
X(i,:) = Xnewm(i,:);%eq.(20)
fitness(i) = fobj(Xnewm(i,:));
end
end
% Strategy 2: Anti-predator strategies(APS-f)
for i=1:Nf
for j=1:1:dim
rand_leader_index = floor(Nf*rand()+1);
X_randf = Xf(rand_leader_index, :);
flag_index = floor(2*rand()+1);
Flag=vec_flag(flag_index);
Af=exp(-fitness_f(rand_leader_index)/(fitness_f(i)+eps));
Xnewf1(i,j)=X_randf(j)+Flag*C2*Af*((ub(1)-lb(1))*rand+lb(1));%eq.(4)
end
Xnewf2(i,:)=X(i,:)+rand(1,1) .* (Xbest_f-round(1+z).*X(i,:)); % Eq.(18)
Xnewf2(i,:) = max(Xnewf2(i,:),lb_ap);Xnewf2(i,:) = min(Xnewf2(i,:),ub_ap);
if fobj(Xnewf2(i,:)) < fobj(Xnewf1(i,:))%Eq.(18)
Xnewf(i,:)=Xnewf2(i,:);%Eq.(18)
else
Xnewf(i,:)=Xnewf1(i,:);%Eq.(18)
end
if(fobj(Xnewf(i,:))<fobj(Xbest_f))%eq.(20)
X(i,:) = Xnewf(i,:);%eq.(20)
fitness(i) = fobj(Xnewf(i,:));
end
end
.................................................✅作者简介:信号处理方向在校博士研究生,目前专研于MATLAB算法及科学绘图等,熟知各种信号分解算法、神经网络时序、回归和分类预测算法、数据拟合算法以及滤波算法。提供一个可以相互学习相互进步的平台
🚩技术信仰:知行合一,让每一行代码都成为解决问题的利器
关注"MATLAB科研小白 "后联系博主私家定制