课堂开头介绍 assignment3 part3
简单说,设计一个并行渲染器,渲染一张 1000 x 1000 的图片。
输入是大量圆圈的中心 xy 坐标、半径、颜色
简单来说,我们要计算每个圆圈会占据的像素点,然后给这些像素点染色

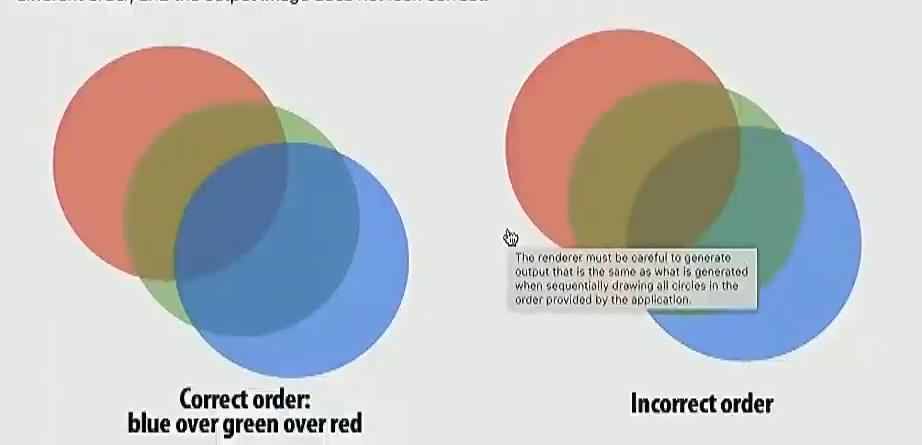
让这个问题变得有趣的地方是,圆圈之间会重叠,会重叠的圆圈最终效果和覆盖顺序是有关联的,需要在并行情况下正确处理这些顺序:
接下来开始这堂课的内容:
一开始教授先带我们复习一下 DNN 的内容。太基础的知识我没记。
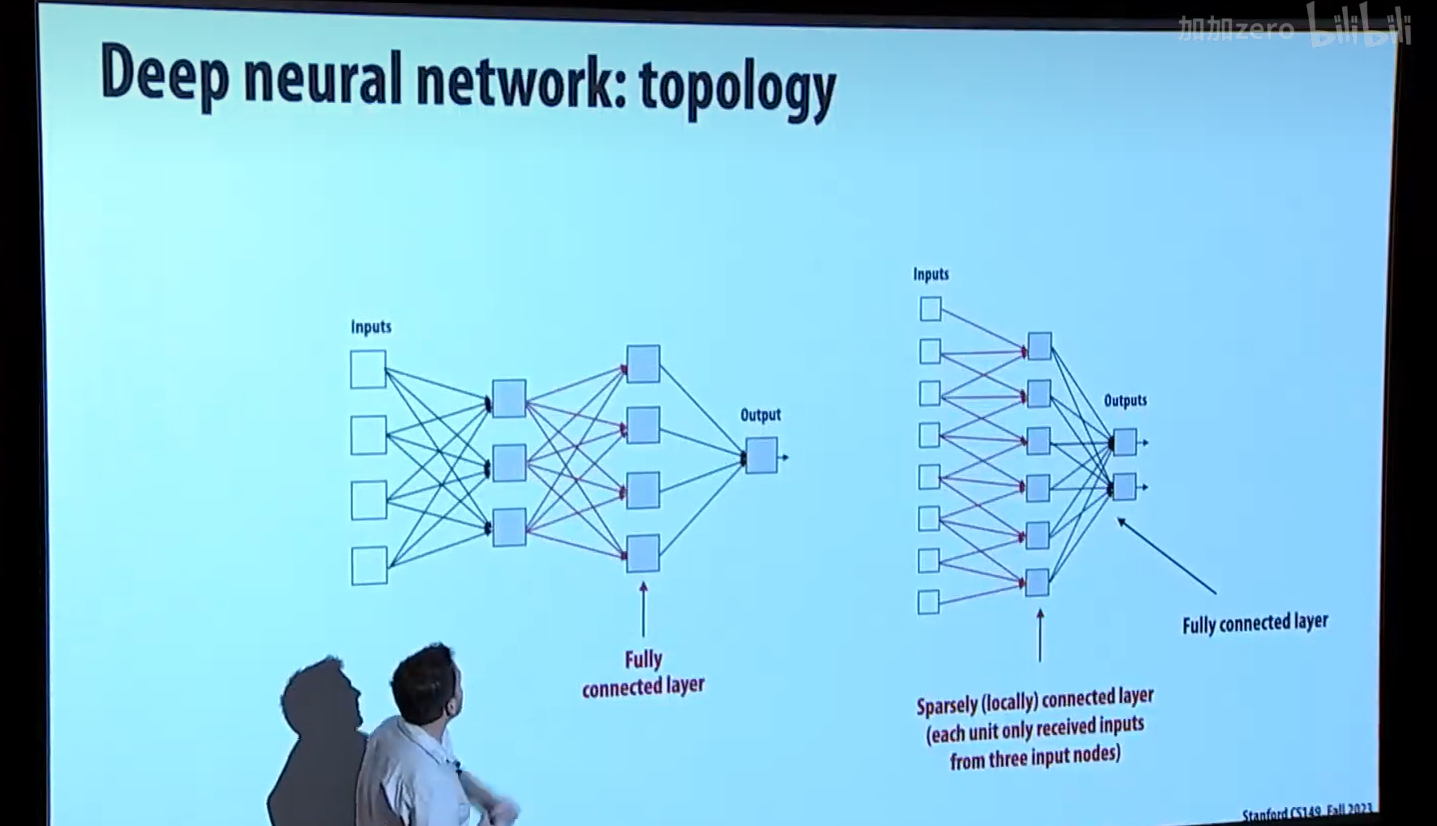
下面是全连接层和稀疏连接层的差别:
下图是一个二维卷积算法,输出图像的每一个点是输入图像的9个点的平均值,它会让图片模糊化:

解释 "卷积层" 的一个更好的图:

教授随后介绍了现代神经网络往往有很多层,涉及到大量卷积计算。
这部分不需要抠细节,教授只是意图让我们明白 卷积 计算的重要性,说明为什么对 DNN 进行并行化很重要。
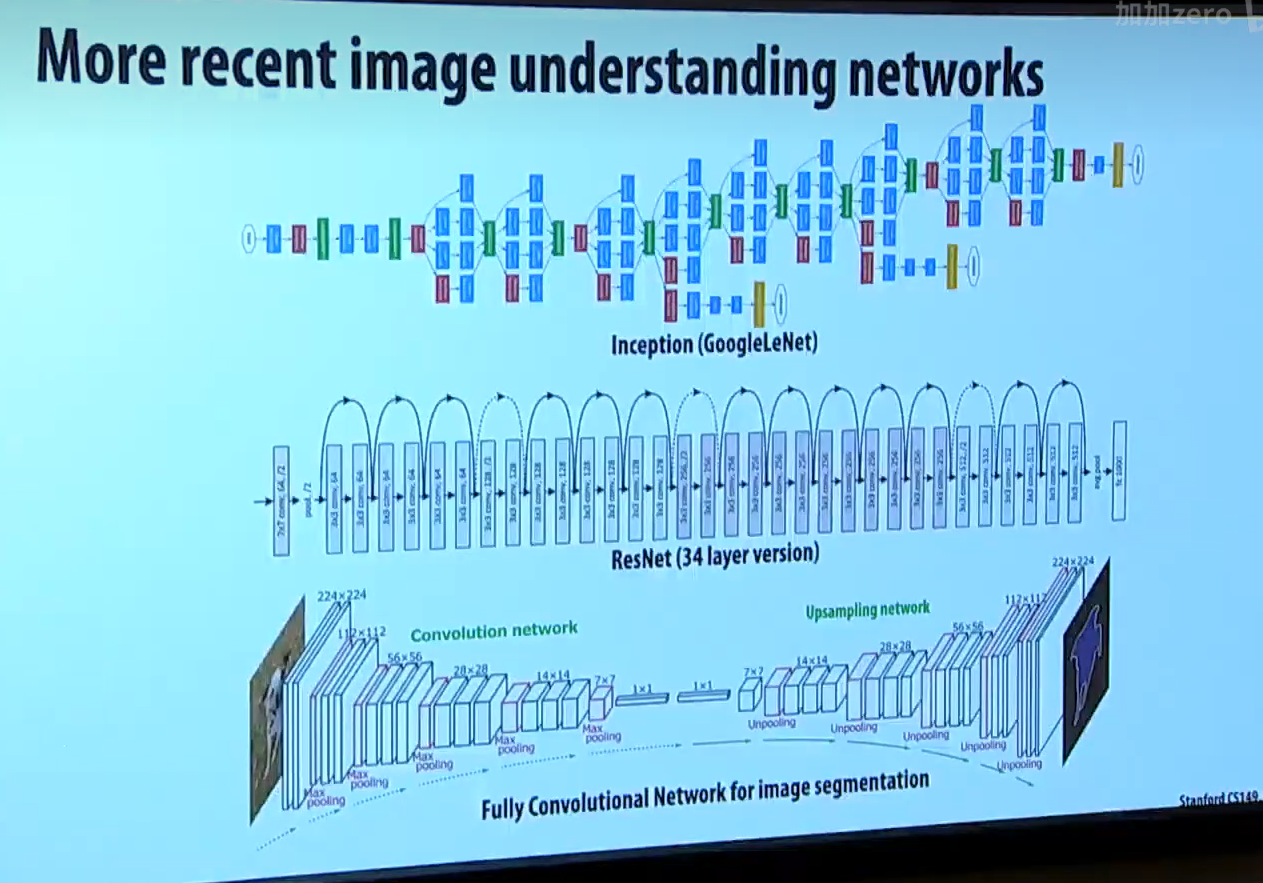
已知卷积层在机器学习中很常见,那么,如何高效实现卷积层呢?
一共有三种方法,下面一一介绍。

第一种方法:提出新的机器学习算法,在算法层面上更快、更精准、更有效

事实上,作为 mlsys 工程师,跟踪最新的 AI 算法很重要。
2014 -> 2017 四年间,算法层面的提升达到了 25 倍,硬件在这段时间里可不会块 25 倍。
如果你在 2014 年针对 VGG-16 做并行优化,那么几年后的新算法可能已经让你的并行优化变得毫无意义。
不过这和这门课内容无关,了解即可

第二种方式与这门课高度相关,我们要在现代机器上高效实现神经网络算法

下面是一个带有批处理的卷积层实现,这是一个正确但性能很烂的实现,只是放这里让大家了解

下图是把 3x3 卷积计算转换成两个矩阵的乘法,这样我们能利用很多矩阵乘法的并行优化。
如下图,把原始 WxH 的矩阵,转为一个 WxHx9 的矩阵,随后把 9 个 1/9 设置为一个矢量,让两者相乘。乘法结果的每一行的结果都是卷积输出矩阵的元素。

有了这种方法,我们也可以很轻松地添加滤波器,得到不同的滤波效果,且它们都受到矩阵乘法的并行优化加成

如果扩展到多维的输入矩阵,那么我们扩展第一个矩阵的列数和 filters 矩阵的行数即可。
甚至可以让不同通道的图像接收不同的滤波器处理
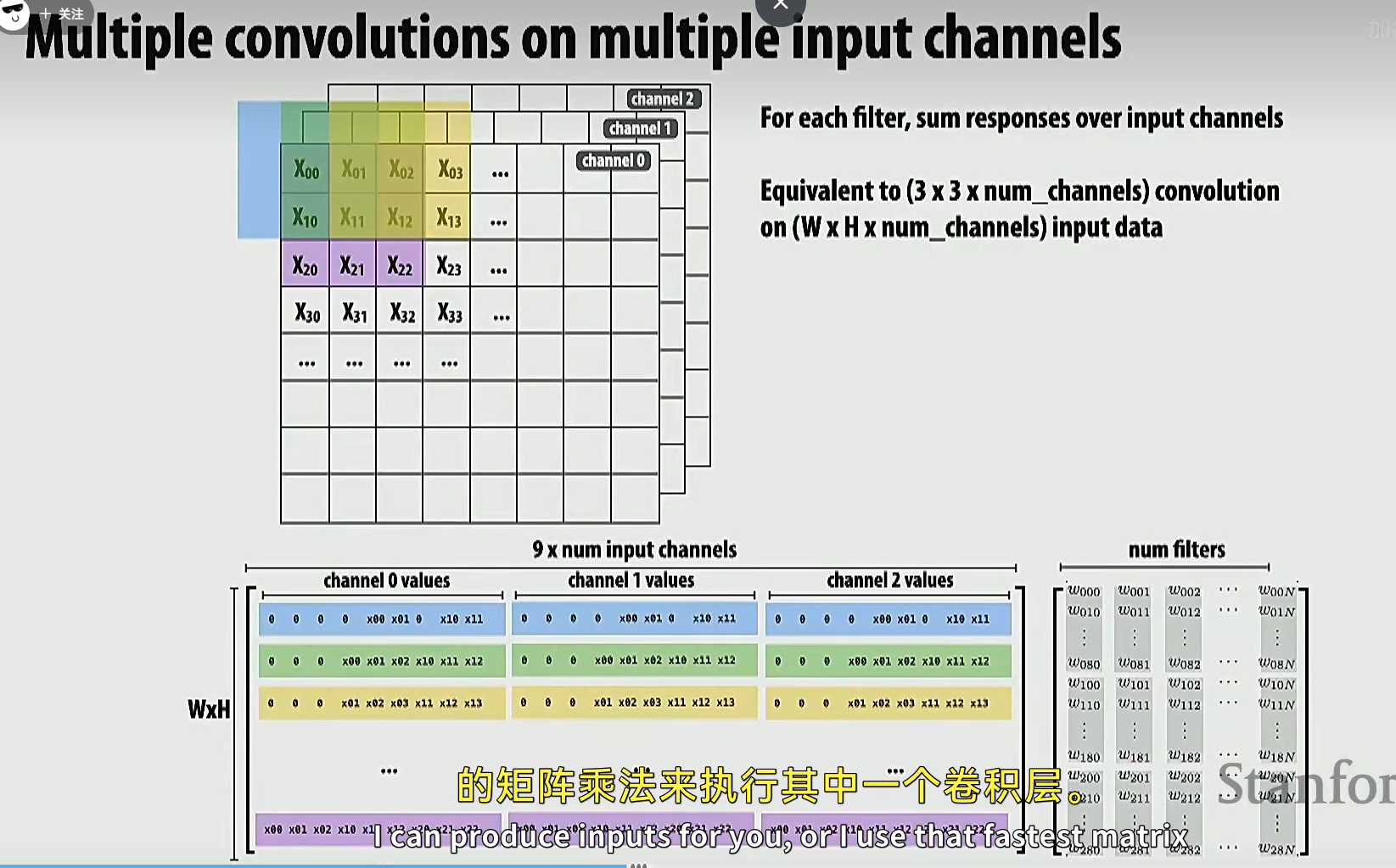
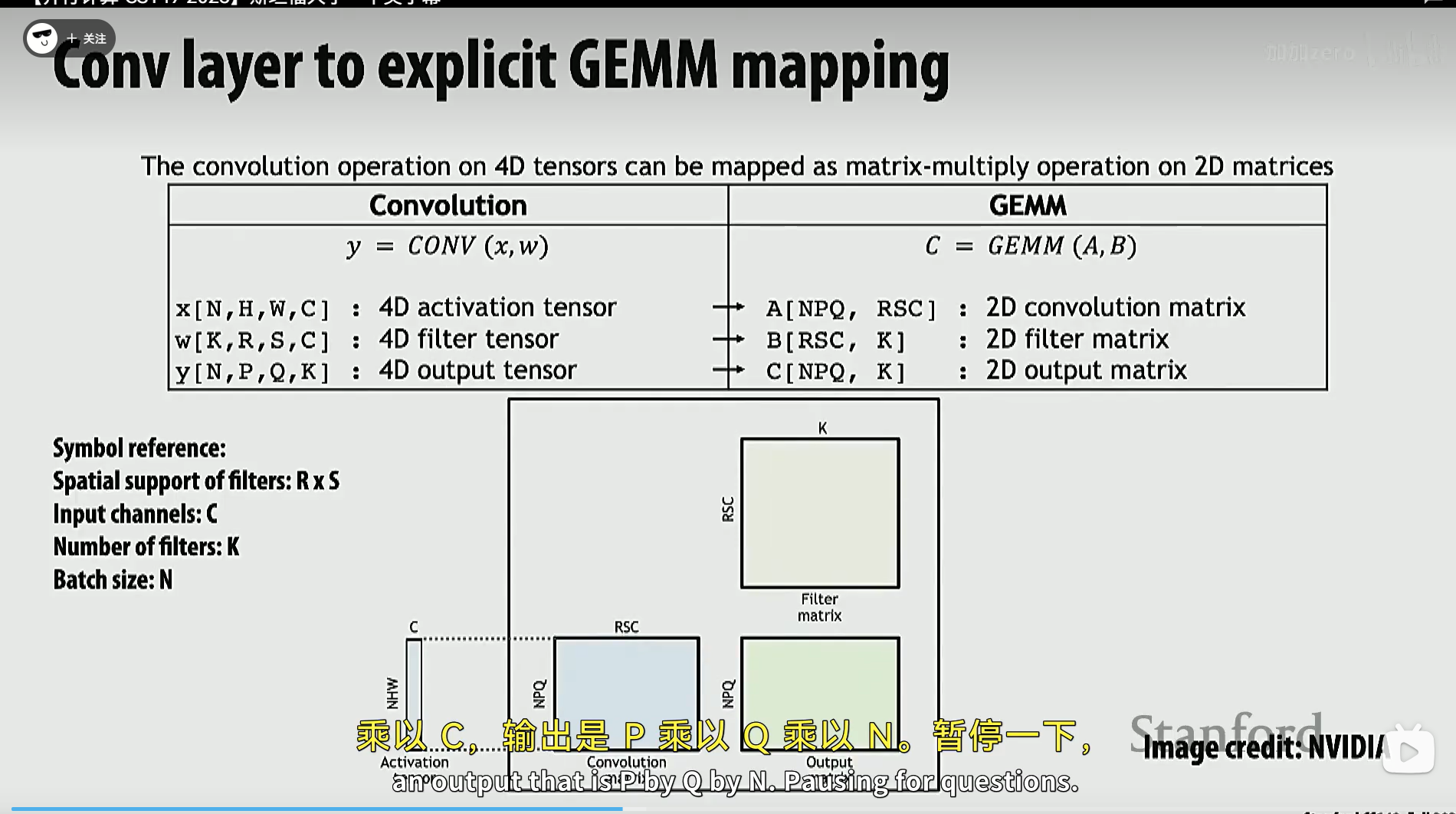
多维张量卷积可以被映射到 2D 矩阵乘法上。
这部分教授没细讲,估计是比较难的内容,研究到再了解吧
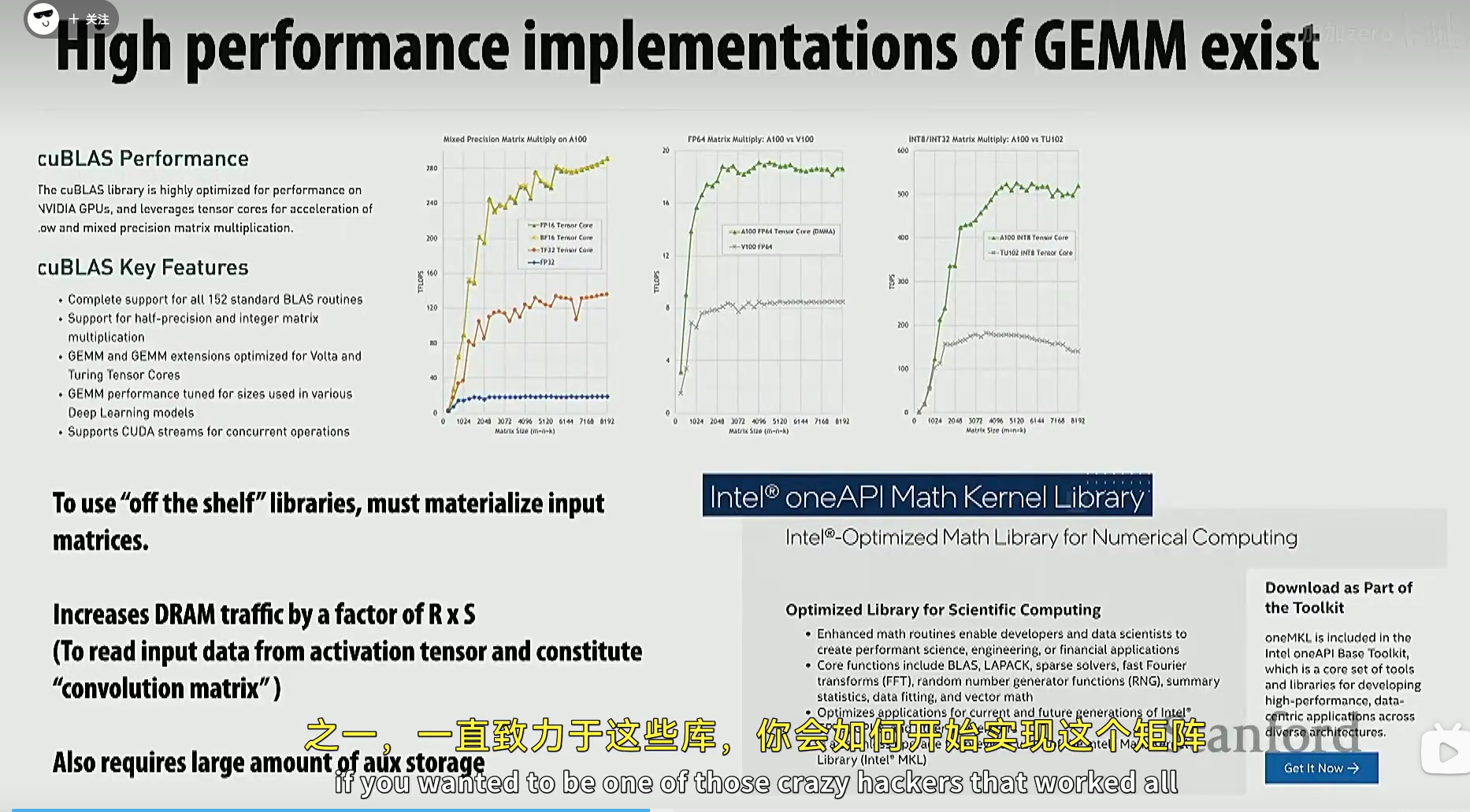
NVIDIA 和 AMD 一直致力于提升 GEMM 的速度,通常你不会写得比他们更快
如下图,是一个简单的稠密矩阵乘法。
它的问题:B 矩阵的访问在内存布局中是不连续、跳跃的,cache miss 概率大大增加,从而降低性能。
也可以用另一个视角来分析。性能优化中有一个概念叫做 arithmetic intensity,算数强度。算数强度是浮点数运算次数和内存访问字节数的比值。通常算术强度越大越好。
我们分析这个问题,我们一共访问了三个矩阵的数据,因此内存访问应该是 3N^2 也就是 O(N^2)。而计算一共有 N^3,因为有三层 N 循环。也就是算术强度理论上应该是 O(N^3 / N^2) = O(N)。
但下图的代码不是。由于 B 矩阵的元素访问存在大量不连续的跳跃,我们可以当作 B 矩阵的元素内存访问都会发生 cache miss。我们看最内层循环,有一个加法和一个乘法,也就是两次浮点数操作,同时也有内存访问 B 的元素。而一共有三层循环,因此可以认为浮点数运算有 2*N^3, 内存访问数量也是 N^3。因此实际的算术强度是 O(1)。这也是证明算法性能不佳的一个角度。

一种好的处理方式是分块乘法。把每个分块分到 cache 能容纳的程度。
那么对于小分块(大小为 B),来说,算术强度就是 O(B)。
块越大越好吗?这个答案是肯定的,假设小分块大小为 1,那么算术强度就是 O(1),小分块大小为 N,算术强度就是 O(N)。根据算术强度越大越好的理论,小分块肯定越大越好,但前提是能够被 cache 容纳。

教授说,经过实验,当问题规模足够大时,这两种实现方式有几百上千倍的速度差异。
考虑到现代 CPU/GPU 往往有多级 cache,实际上我们可以为每级 cache 做专门的分块,这也能带来一定的性能提升。但通常一级划分就能带来很大提升了。

事实上,还可以用 SIMD 来并行化矩阵乘法,这里可以使用 "矢量切片" 来把矩阵切成一个一个矢量。
这里面涉及到一些转置之类的操作,了解即可,不用过于深入。



现代工业级神经网络可能会为每一层网络做特定的性能并行优化。

回到之前的 slides,你会注意到,为了把卷积转为普遍的矩阵乘法,我们把原本较小的矩阵扩展成了大得多的新矩阵,这可能会带来数十倍的内存开销。实际上我们不会这么做。

如下图的实现,实际上,我们实现了一个数学转换器,它可以在运算时计算出 "扩展后大矩阵" 里的元素对应于 "原本小矩阵" 的哪一个元素,从而节约内存开销。
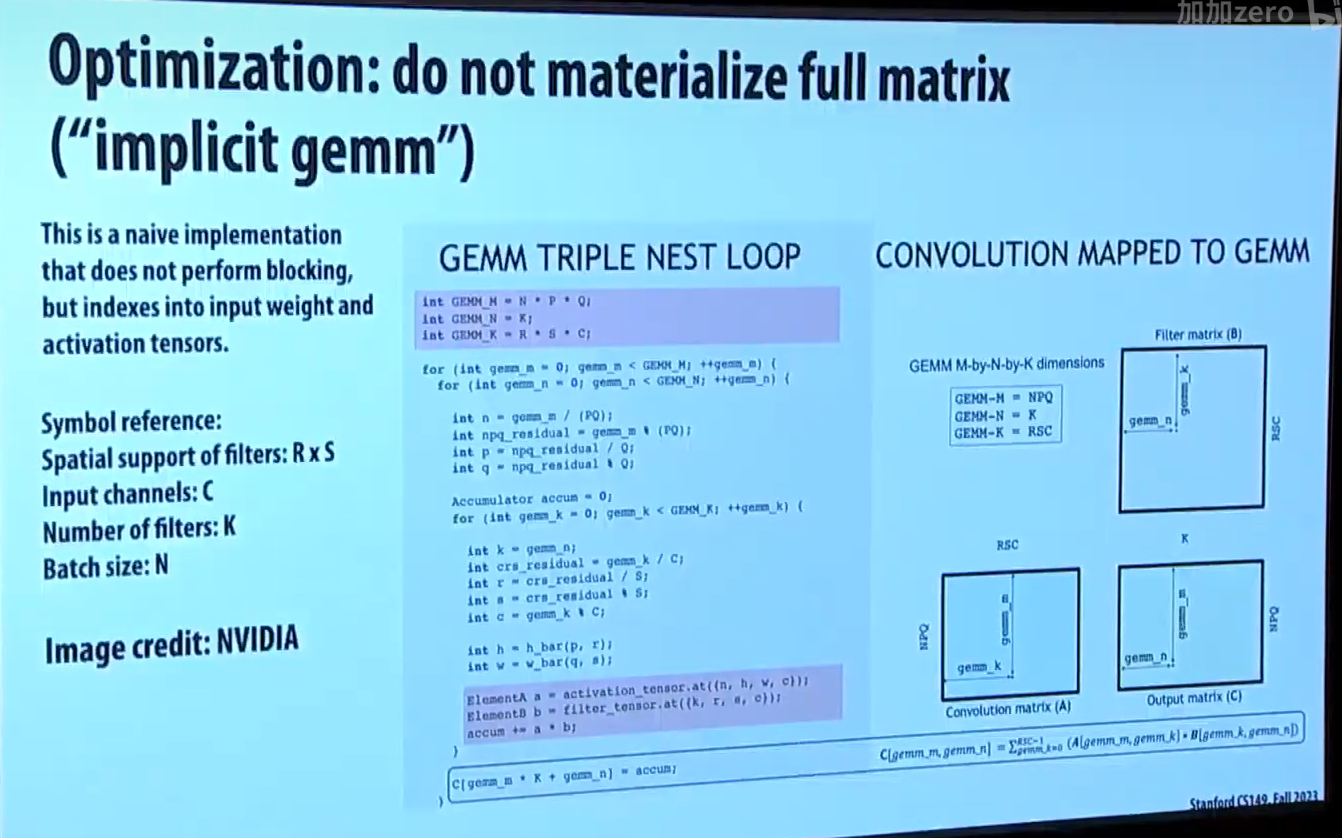
英伟达提供了一个库,CUTLASS,主要是提供速度快的矩阵乘法库

批处理操作存在的原因:单批次的矩阵运算量可能只会用到 GPU 上的几个 SM。GPU 上仍有相当多的 SM 出于空闲状态。这也是为什么要批次化,我们希望能够让 GPU 的更多部分被利用起来,从而得到更多的性能。

一个算法上的提升:卷积操作也可以在傅里叶域上实现。
这里的优化利用了快速傅里叶变化的思想。
比较难,也不是重点,教授没细节,了解一下就行

英伟达的核心库 cuDNN 提供了包装好的卷积库、矩阵运算库。tensorflow 和 pytorch 通常都会被转换为这些 API 的调用。

这是一个计算卷积的 cuDNN API 例子

现代神经网络往往有很多层,甚至达到几百层,这会导致一个问题:过大的内存IO操作。
以下图为例子,我们先从内存读取一个大矩阵,做完卷积后,把输出结果存放到内存,随后又读出,做 scale/bias,再把结果存放到内存,再读出,做最大池化。如此多的内存 IO 操作会导致程序变成 "带宽受限" 程序。 (你可以把这里的内存 IO 看作 load/store 汇编指令,这样能更好地理解性能开销。)
一个比较好的解决方案是把几层神经网络的操作混合在一起。
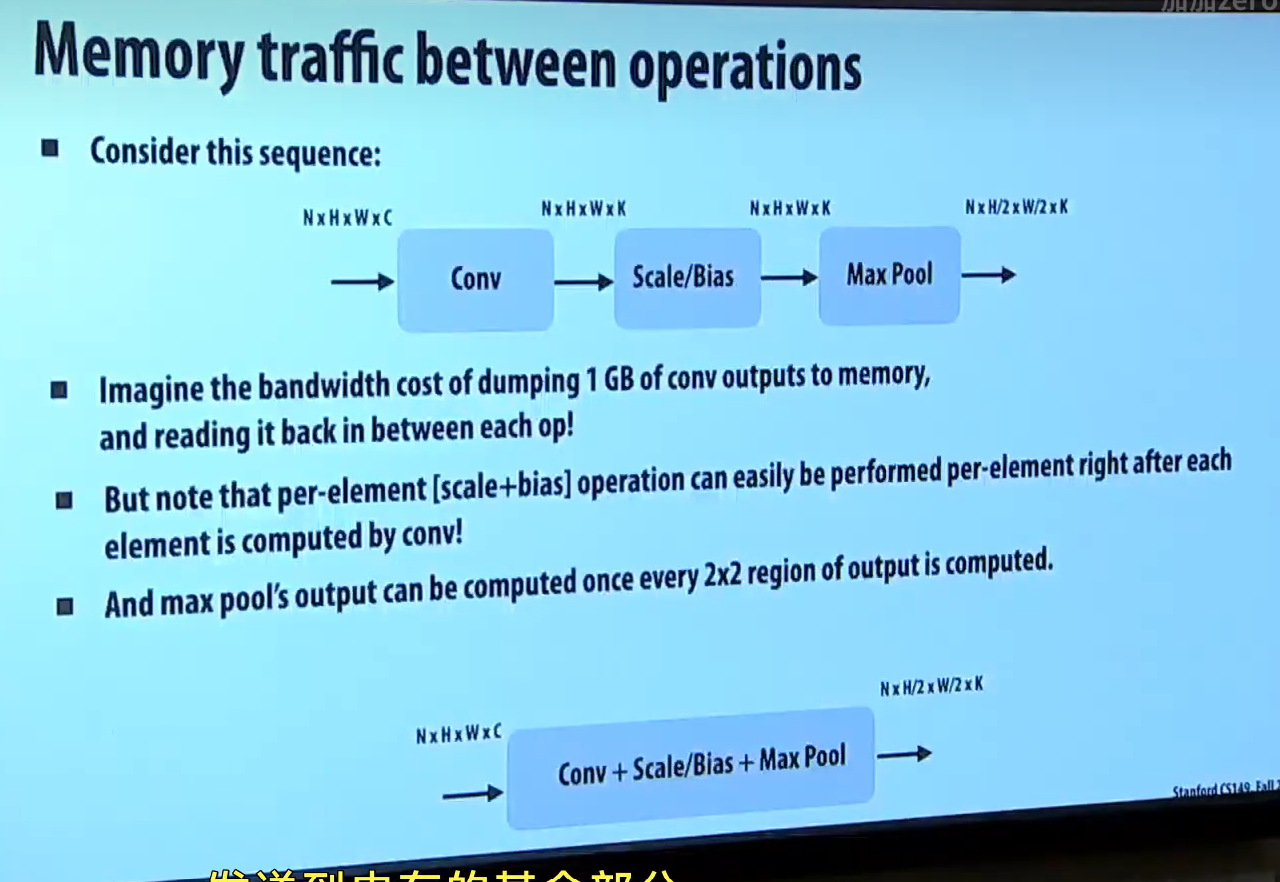
如下图,这是一个把卷积 + scale/bias + 最大池化融合在一起的融合层代码。从汇编层面上,它会省去一些 load/store 指令。

接下来介绍一个优化例子,这个优化能大幅提升 LLM 中的 Transformer 的性能

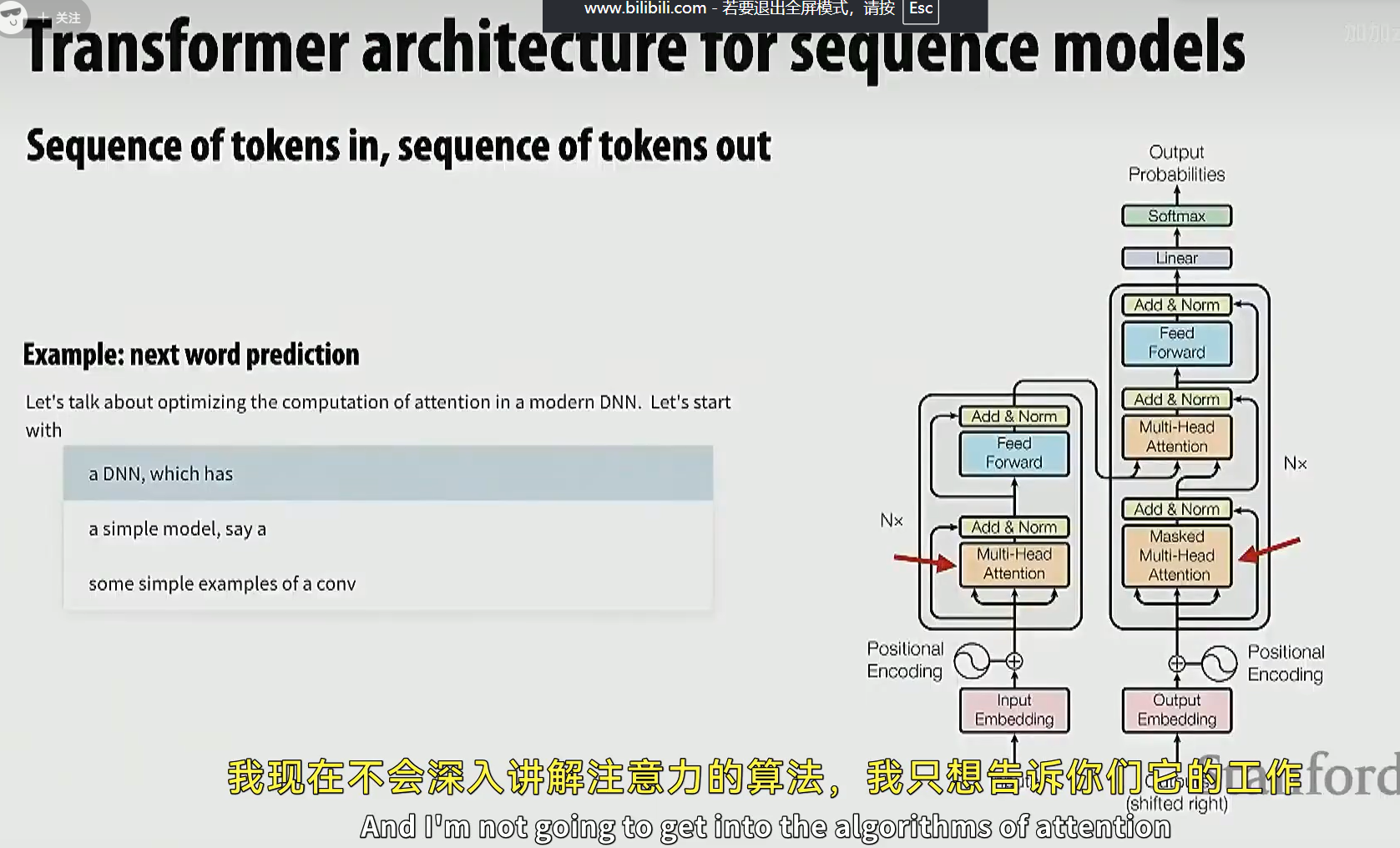
这里的 Transformer 是一个 "序列到序列" 的 Transformer。
我们需要重点关注的是一个叫 "自注意力" 的模块。
注意力模块如下图。Q, K, V 都是 N x d 的矩阵
分为三步计算:
1.S = QK^T
2.P = softmax(S)
3.O = PV
至于它到底是做什么的,我们暂时先不关心。
slide 右边是对 softmax 函数的解释

计算注意力的流程如下:
先计算 QK^T,再计算这个 NxN 矩阵的 softmax 结果,接着再计算 O = PV
矩阵非常大,可以很自然地想到分块计算。
但这个过程仍涉及到大量内存读写。
如果能把多个步骤的计算融合在一起,那么也能提升性能。
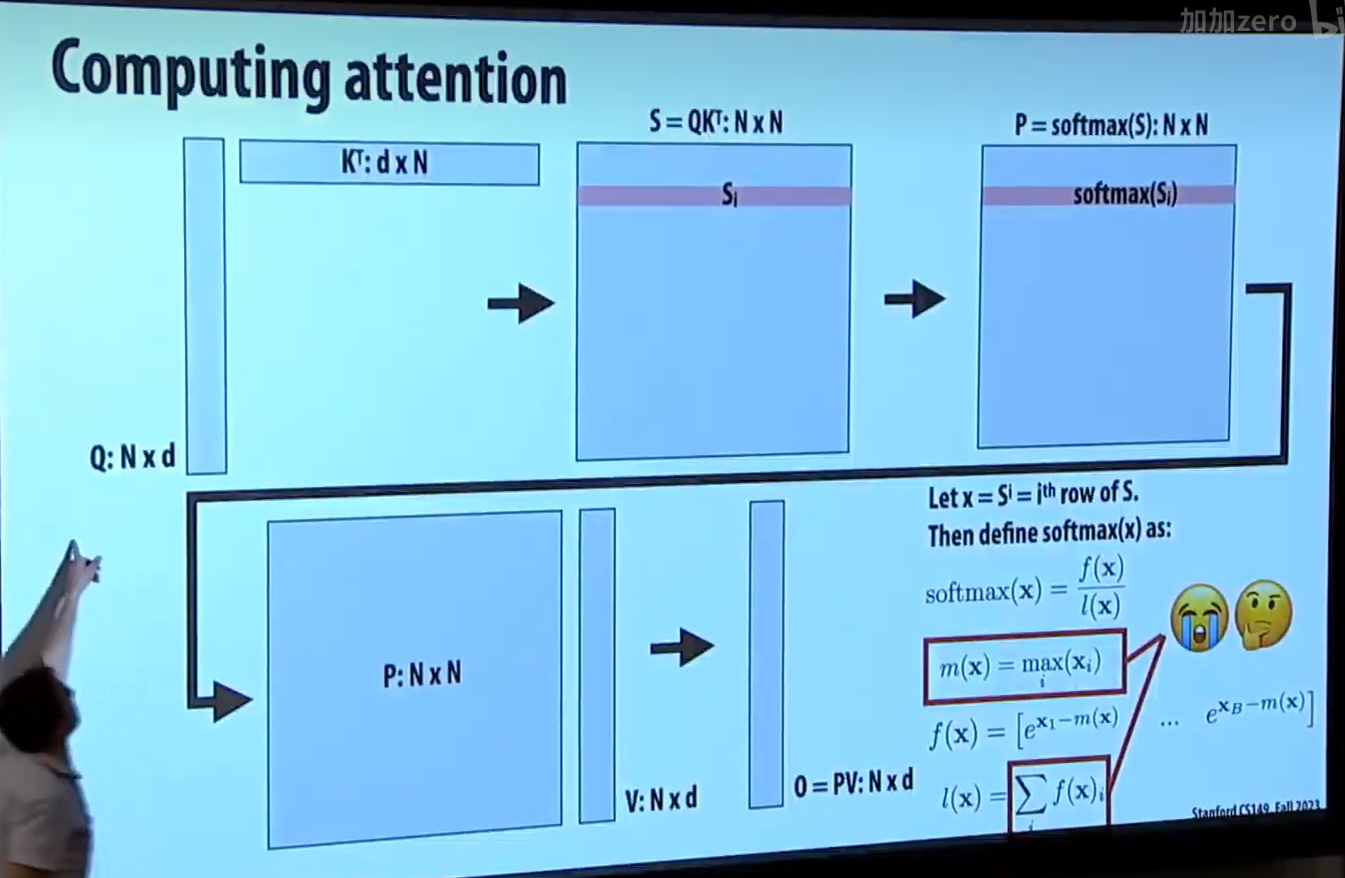
在下图中,你可以看到 softmax 的计算是可以分块计算的。

发现 softmax 可以分块计算后,就可以很自然的把整个 pipeline 融合,从而提高算术强度,降低内存占用,且在某些情况下提升性能。

接下来我们看看现代 DNN 框架里的融合操作

老版本的时候,融合操作通常靠 hardcode 的API 提供
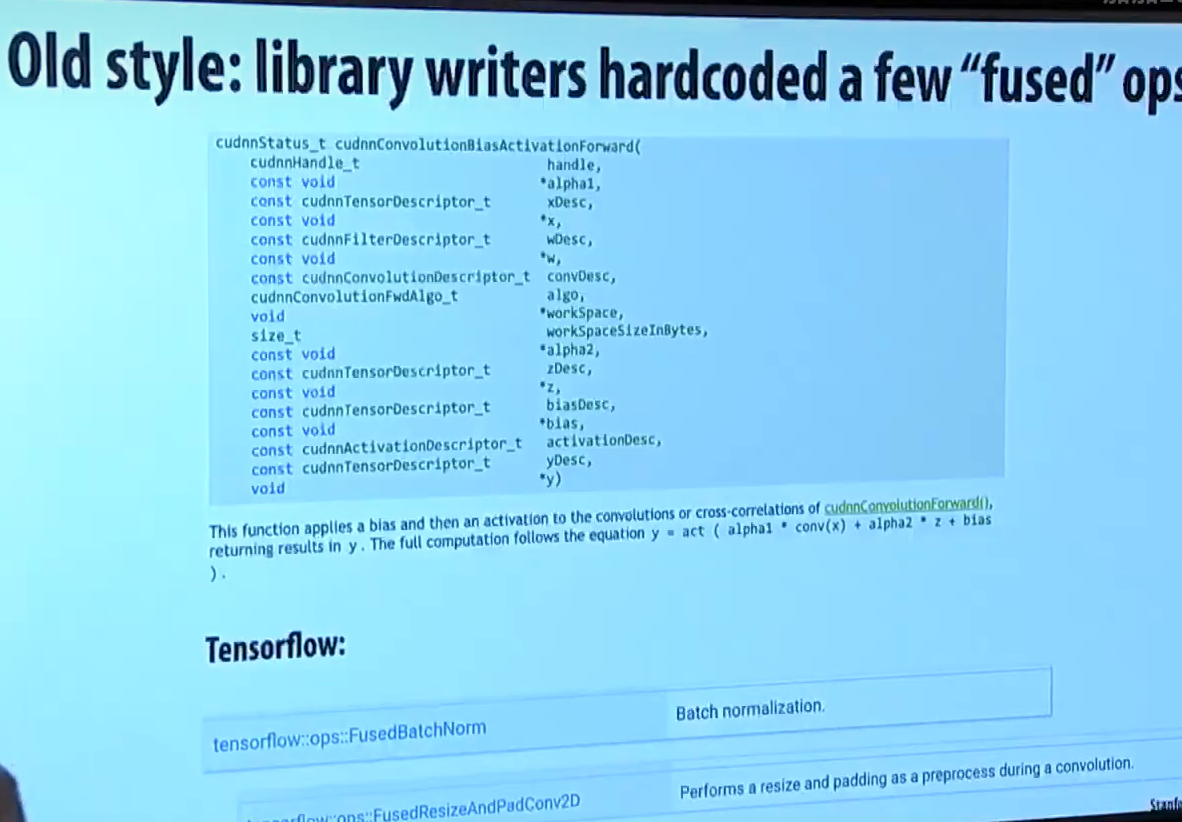
CUDA 编译器会检测卷积操作后面是否跟着 "point-wise" 操作,若有,就自动融合

更先进的 compilers 可以做更多优化

尝试用更低精度的计算来提升神经网络速度

如果你是做 mlsys的,那么第一个任务就是了解最新最好的算法。如果你从被淘汰的算法开始优化,那么你很容易落伍。

接下来介绍点 GPU 硬件的知识。
GPU 不是专门为神经网络设计的硬件,为什么是好的评估优化平台呢?

英伟达自己做过一个评估:
如果仅仅在 GPU 上计算乘法加法,那么性能比乘法加法专用电路慢 20倍
如果加上内积,那么性能比专用电路慢 5倍
如果加上 4x4 矩阵乘法,那么只比专用电路慢 27%

因此,英伟达选择在 GPU 上加张量核心,而非设计专用的神经网络处理器
