两个数组的dp问题

文章目录

正则表达式匹配
交错字符串
两个字符串的最小ASCII删除和
最长重复子数组
最长公共子序列
不相交的线
不同的子序列
通配符匹配
总结

正则表达式匹配

一、题目解析

给定一个字符串s和一个正则表达式p，实现一个支持'.'和'*'的正则表达式匹配。其中：

'.'可以匹配任意单个字符。
'*'表示前面的元素可以出现任意次（包括 0 次）。

二、算法原理

状态表示

用dp[i][j]表示：p中[0, j]区间内的子串是否能够匹配s中[0, i]区间内的子串，值为true或false。
状态转移方程

根据p最后一个位置的状态，分情况讨论：

若p[j]是普通字符（非'.'和'*'）：则需p[j] == s[i]且dp[i - 1][j - 1] == true，此时dp[i][j] = true。
若p[j] == '.'：则dp[i][j] = dp[i - 1][j - 1]。
若p[j] == '*'：
- 当p[j - 1]重复 0 次时，dp[i][j] = dp[i][j - 2]。
- 当p[j - 1]重复至少 1 次时，需p[j - 1]能匹配s[i]（p[j - 1] == s[i]或p[j - 1] == '.'）且dp[i - 1][j] == true，此时dp[i][j] = dp[i - 1][j]。

p[j]='*'时，通常是分类p[j-1]为普通字符还是 '.' ，递推过程写出后可以总结为p[j-1]重复次数。

初始化

引入空串，确保后续填表逻辑正确。
处理边界情况，如下标转移等，例如让s = " " + s，p = " " + p。
（0，0）两空串能匹配
（i，0) p为空，s不为空时，全false
（0，j)s为空，当p为空时（当偶数位全是'*'时，p为空），true

填表顺序

从上往下填写每一行。
每一行从左往右填写。
根据状态转移方程，dp[i][j]由dp[i-a]j-b推导而来，也就是根据左上角的状态推导，故而上--》下，左--》右。

返回值
返回dp[m][n]（m为s的长度，n为p的长度）。

写状态转移方程时，都是根据p最后位置的状态分类讨论的，可以直接边讨论边写，最后再把情况相似的优化。

我这里的m n 是原串长度+1，所以最后返回(m-1,n-1)

cpp 复制代码

class Solution {
public:
    bool isMatch(string s, string p) {
         
        //引入空串，防止越界
        s=" "+s;
        p=" "+p;
       int m=s.size(),n=p.size();
        vector<vector<bool>>dp(m,vector<bool>(n,false));

        //初始化
        dp[0][0]=true;
        for(int j=2;j<n;j+=2)//s为空串
        {
                if(p[j]=='*')dp[0][j]= true;
                else break;
        }

        for(int i=1;i<m;i++)
        for(int j=1;j<n;j++)
        {//最后为. 或 普通字符
            if(p[j]==s[i]||p[j]=='.')dp[i][j]=dp[i-1][j-1];
            else if(p[j]=='*')//最后为*
            {
                if(p[j-1]=='.')
                {
                    //dp[i][j]=dp[i][j-2]||dp[i-1][j-2]||dp[i-2][j-2]||dp[i-3][j-2].....
                    //同理可得-> dp[i-1][j]=dp[i-1][j-2]||dp[i-2][j-2]||... 所以
                    dp[i][j]=dp[i][j-2]||dp[i-1][j];
                }
                else{
                    //p[j-1]是普通字符: 和*组合起来，可以匹配0个/n个
                    dp[i][j]=dp[i][j-2]||(p[j-1]==s[i]&&dp[i-1][j]);

                }
            }
        }
        return dp[m-1][n-1];
    }
};

交错字符串

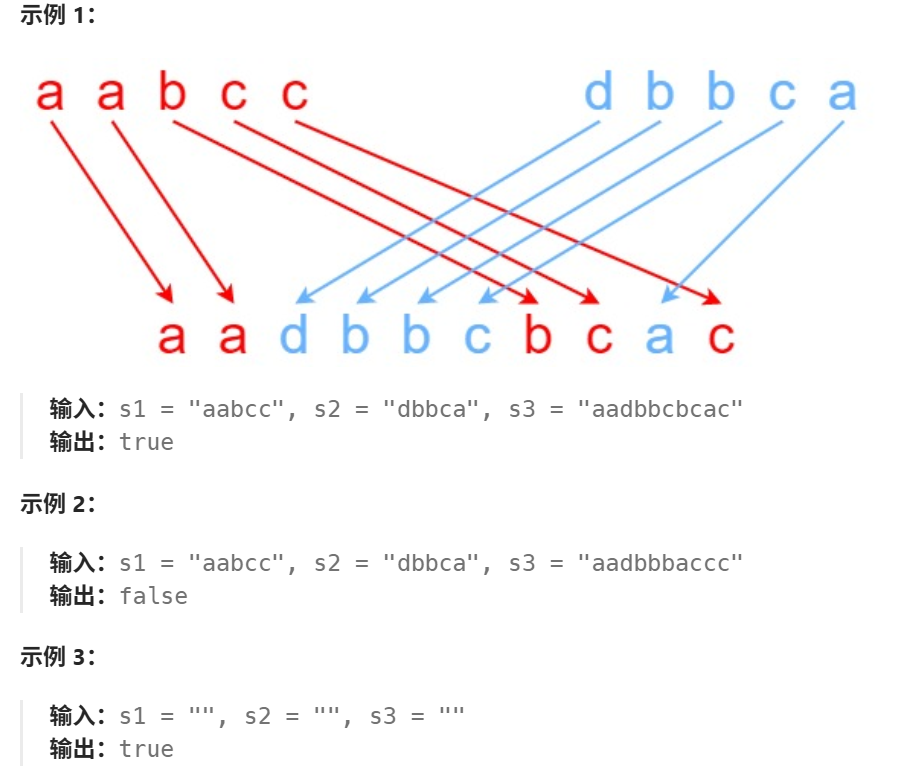
一、题目解析

给定三个字符串 s1、s2、s3，需判断 s3 是否能由 s1 和 s2 交替拼接而成。

二、算法原理（动态规划）

预处理
为了方便后续处理边界情况，对三个字符串进行预处理，给每个字符串前面添加一个空字符，即 s1 = " " + s1，s2 = " " + s2，s3 = " " + s3。
状态表示
用 dp[i][j] 表示：s1 中 [1, i] 区间内的字符以及 s2 中 [1, j] 区间内的字符，能否拼接成 s3 中 [1, i + j] 区间内的字符。
状态转移方程
根据拼接的最后一个位置的字符来源，分情况讨论：

若最后一个字符来自 s1，即 s1[i] == s3[i + j]，且 dp[i - 1][j] == true，那么 dp[i][j] = true。
若最后一个字符来自 s2，即 s2[j] == s3[i + j]，且 dp[i][j - 1] == true，那么 dp[i][j] = true。

状态转移方程推到的时候，不要并列顺序写这两种情况，因为它们只要有一个是true,那结果就是true。是或（||）的关系。

if(s1[i]==s3[i+j])dp[i][j]=dp[i-1][j];

if(s2[j]==s3[i+j])dp[i][j]=dp[i][j-1];(X )

dp[i][j]=(s1[i]==s3[i+j]&&dp[i-1][j])||

(s2[j]==s3[i+j]&&dp[i][j-1]);

初始化
构建一个二维表格来存储状态，初始时表格中的值需要根据实际情况进行合理初始化，以保证后续状态转移的正确性。
填表顺序

从上往下填写每一行。
每一行从左往右填写。

返回值
最终的结果由 dp[m][n] 决定，其中 m 是 s1 的长度，n 是 s2 的长度，它表示 s1 全部字符和 s2 全部字符能否拼接成 s3 全部字符。

cpp 复制代码

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
        int m=s1.size(),n=s2.size();
        if(m+n!=s3.size())return false;
        //加空串方便填表
        s1=" "+s1,s2=" "+s2,s3=" "+s3;

        vector<vector<bool>>dp(m+1,vector<bool>(n+1,false));
        //初始化
        dp[0][0]=true;
        for(int i=1;i<=m;i++)
        {
            if(s1[i]==s3[i])dp[i][0]=true;
            else break;
        }
        for(int j=1;j<=n;j++)
        if(s2[j]==s3[j])dp[0][j]=true;
        else break;

        //状态转移方程
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
               
                dp[i][j]=(s1[i]==s3[i+j]&&dp[i-1][j])||
                (s2[j]==s3[i+j]&&dp[i][j-1]);
            }
        }

        return dp[m][n];

    }
};

两个字符串的最小ASCII删除和

题目解析

问题描述：给定两个字符串 s1 和 s2，返回使两个字符串相等所需删除字符的 ASCII 值的最小和。
分析：求两个字符串里面所有的公共子序列里面，ASCII 值的最大和。最后再用整体的ASCII值-最大*2

算法原理

1.状态表示
dp[i][j] 表示：s1 的 0...i 区间以及 s2 的 0...j 区间内的所有子序列里，公共子序列的 ASCII 最大和。

2.状态转移方程

根据最后一个位置的状况，分情况讨论：
有 s1[i]，有 s2[j] → s1[i] == s2[j] → dp[i][j] = dp[i-1][j-1] + s1[i]
有 s1[i]，有 s2[j] → s1[i] != s2[j] → dp[i][j] = max(dp[i-1][j], dp[i][j-1])
没有 s1[i]，有 s2[j] → dp[i][j] = dp[i-1][j]
没有 s1[i]，没有 s2[j] → dp[i][j] = dp[i][j-1]
3,4的情况包含到2中了

3.初始化

下标的映射关系 → i 减 1

4.填表顺序

从上往下填写每一行，每一行从左往右。

5.返回值

dp[m][n]
统计 2 个字符串的 ASCII 和 → sum
sum - dp[m][n] * 2

cpp 复制代码

class Solution {
public:
    int minimumDeleteSum(string s1, string s2) {
        int m=s1.size(),n=s2.size();
        vector<vector<int>>dp(m+1,vector<int>(n+1,0));

        for(int i=1;i<=m;i++)
        for(int j=1;j<=n;j++)
        {
dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
if(s1[i-1]==s2[j-1])dp[i][j]=max(dp[i][j],dp[i-1][j-1]+s1[i-1]);
        }
    int sum1=0,sum2=0;
        for(auto e:s1)sum1+=e;
        for(auto e:s2)sum2+=e;

        return sum1+sum2-2*dp[m][n];

    }
};

最长重复子数组

一、题目解析

给定两个整数数组 nums1 和 nums2，需找出它们的最长连续公共子数组的长度。

示例：nums1 = [1,2,3,2,1]，nums2 = [3,2,1,4,7]，最长重复子数组为 [3,2,1]，长度为 3。

二、算法原理

状态表示
dp[i][j]：以 nums1 第 i 个元素、nums2 第 j 个元素结尾的最长重复子数组长度。

这里无法找区间内的最长重复子数组，只能是以i/j为结尾找。因为子数组要是连续的，就算最后的位置相同，前面不连续结果也是0。子序列不要求连续就可以通过范围定状态表示。

状态转移方程

若 nums1[i-1] != nums2[j-1]：无法形成连续重复子数组，dp[i][j] = 0。
若 nums1[i-1] == nums2[j-1]：可延长之前的重复子数组，dp[i][j] = dp[i-1][j-1] + 1。

初始化

创建 (m+1)×(n+1) 的 dp 数组（m、n 为数组长度），所有元素初始化为 0。
填表顺序

从上到下、从左到右遍历填充 dp 数组。
返回值

遍历 dp 数组，返回其中的最大值（所有可能的最长重复子数组长度）。

cpp 复制代码

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int m=nums1.size(),n=nums2.size();

        //以 nums1 第 i 个元素、nums2 第 j 个元素结尾的最长重复子数组长度。
        vector<vector<int>>dp(m+1,vector<int>(n+1,0));
        int res=0;
        for(int i=1;i<=m;i++)
        for(int j=1;j<=n;j++)
        {
            
            if(nums1[i-1]==nums2[j-1])dp[i][j]=dp[i-1][j-1]+1;
            else dp[i][j]=0;

            res=max(res,dp[i][j]);
        }

        return res;
    }
};

最长公共子序列

状态表示：

dp[i][j]：s1的（0，i)区间，与s2的（0，j)区间中，最长公共子序列的长度。

子序列不要求连续，直接按区间讨论就行

cpp 复制代码

class Solution {
public:
    int longestCommonSubsequence(string s1, string s2) {
        s1=" "+s1;
        s2=" "+s2;
         int m=s1.size(),n=s2.size();
        vector<vector<int>>dp(m,vector<int>(n,0));

        for(int i=1;i<m;i++)
        for(int j=1;j<n;j++)
        {
            if(s1[i]==s2[j])dp[i][j]=dp[i-1][j-1]+1;
            else
            {
                dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return dp[m-1][n-1];
    }
};

不相交的线

这题看题意其实和上一题找最长公共子序列是一样的。

cpp 复制代码

class Solution {
public:
    int maxUncrossedLines(vector<int>& n1, vector<int>& n2) {
        int m=n1.size(),n=n2.size();
        vector<vector<int>>dp(m+1,vector(n+1,0));

        for(int i=0;i<m;i++)
        for(int j=0;j<n;j++)
        {
            if(n1[i]==n2[j])dp[i+1][j+1]=dp[i][j]+1;
            else
            {
                dp[i+1][j+1]=max(dp[i][j+1],dp[i+1][j]);
            }
        }
        return dp[m][n];
    }
};

不同的子序列

状态表示：

dp[i][j]：s的（0，i）区间的所有子序列中有多少t的（0，j）区间内的子串

状态转移方程：

一样从最后的元素讨论：

s[i-1] == t[j-1]时，

dp[i-1][j-1]：选 s[i-1] 去匹配 t[j-1]，此时需统计「s 前 i-1 个字符匹配 t 前 j-1 个字符」的组合数。
dp[i-1][j]：不选 s[i-1]，此时需统计「s 前 i-1 个字符匹配 t 前 j 个字符」的组合数。

不等时，直接不考虑s的最后字符，再匹配dp[i][j] = dp[i-1][j]。

方便填表引入空串，所有s t的下标都-1

下面代码的i j和上面思路的i j的顺序是相反的

cpp 复制代码

class Solution {
public:
    int numDistinct(string s, string t) {
        s=" "+s;t=" "+t;
        int m=t.size(),n=s.size();
        vector<vector<double>>dp(m,vector<double>(n,0));
        for(int j=0;j<n;j++)dp[0][j]=1;
        for(int i=1;i<m;i++)
        for(int j=1;j<n;j++)
        {
if(s[j]==t[i])dp[i][j]=dp[i-1][j-1]+dp[i][j-1];
else
{
    dp[i][j]=dp[i][j-1];
}
        }
        return dp[m-1][n-1];
    }
};

通配符匹配

状态表示：

dp[i][j]：s的（0,i) 和p的（0，j）区间能匹配。

思路一样是分类讨论p的最后一位，是* ? 或者普通字符。

如果是* 的话可以匹配1/2/3...位字符，

就是dp[i][j] = dp[i-1][j-1] || dp[i-2][j-2] || dp[i-3][j-3] || ...

后面可以直接等量代换，dp[i-1][j]= dp[i-2][j-1] || ...

代换完就是 dp[i-1][j-1] || dp[i-1][j]

其他两类分析比较简单。

再根据分析的动态转移方程，我们知道dp[i][j] 都是由 dp[i-a][j-b] （a,b>0)推导来的，也就是二维表的左上角推到到--》右下角，所以填表顺序（遍历顺序）就是左--》右 && 上--》下

cpp 复制代码

class Solution {
public:
    bool isMatch(string s, string p) {
        s=" "+s;p=" "+p;
        int m=s.size(),n=p.size();
        vector<vector<bool>>dp(m,vector<bool>(n,false));

        dp[0][0]=true;
        int flag=1;
        for(int j=1;j<n;j++)
        {
            if(p[j]=='*')dp[0][j]=true;
            else break;
        }

        for(int i=1;i<m;i++)
        for(int j=1;j<n;j++)
        {
         
          if(p[j]=='*')
            {
                dp[i][j]=dp[i-1][j]||dp[i][j-1];
            }
            else
            {
                if(p[j]==s[i]|| p[j]=='?')dp[i][j]=dp[i-1][j-1];
            }
        }

        return dp[m-1][n-1];
    }
};

总结

1.状态表示：

明确 dp[i][j] 的含义（聚焦 "数组 / 字符串 A 的前i个元素 + 数组 / 字符串 B 的前j个元素" 的属性，如 "能否匹配""最长长度""方案数" 等）。
「子数组（连续）」：常定义为 "以 A [i]、B [j] 结尾" 的状态（利用 "连续性" 约束转移，如「最长重复子数组」）。
「子序列（不连续）」：常定义为 "A [0...i]、B [0...j] 区间内" 的状态（无需连续，只需整体最优，如「最长公共子序列」「不同子序列数」）。

2.状态转移：

核心逻辑：从 "最后一个元素的关系" 入手分类讨论（如字符是否相等、是否为特殊字符*/.等）。
转移方向：根据依赖关系，可能是 "左上角推导"（如dp[i-1][j-1]）、"左侧 / 上侧推导"（如dp[i][j-1]/dp[i-1][j]），或 "多情况合并"（如*匹配 0 次 / 多次的或逻辑）。

3.初始化：

技巧：给原字符串 / 数组前添加 "空串 / 空元素"，将 "空" 的边界情况统一到状态中（避免单独处理i=0或j=0的特殊逻辑）。