leetcode 64 最小路径和

一、题目描述

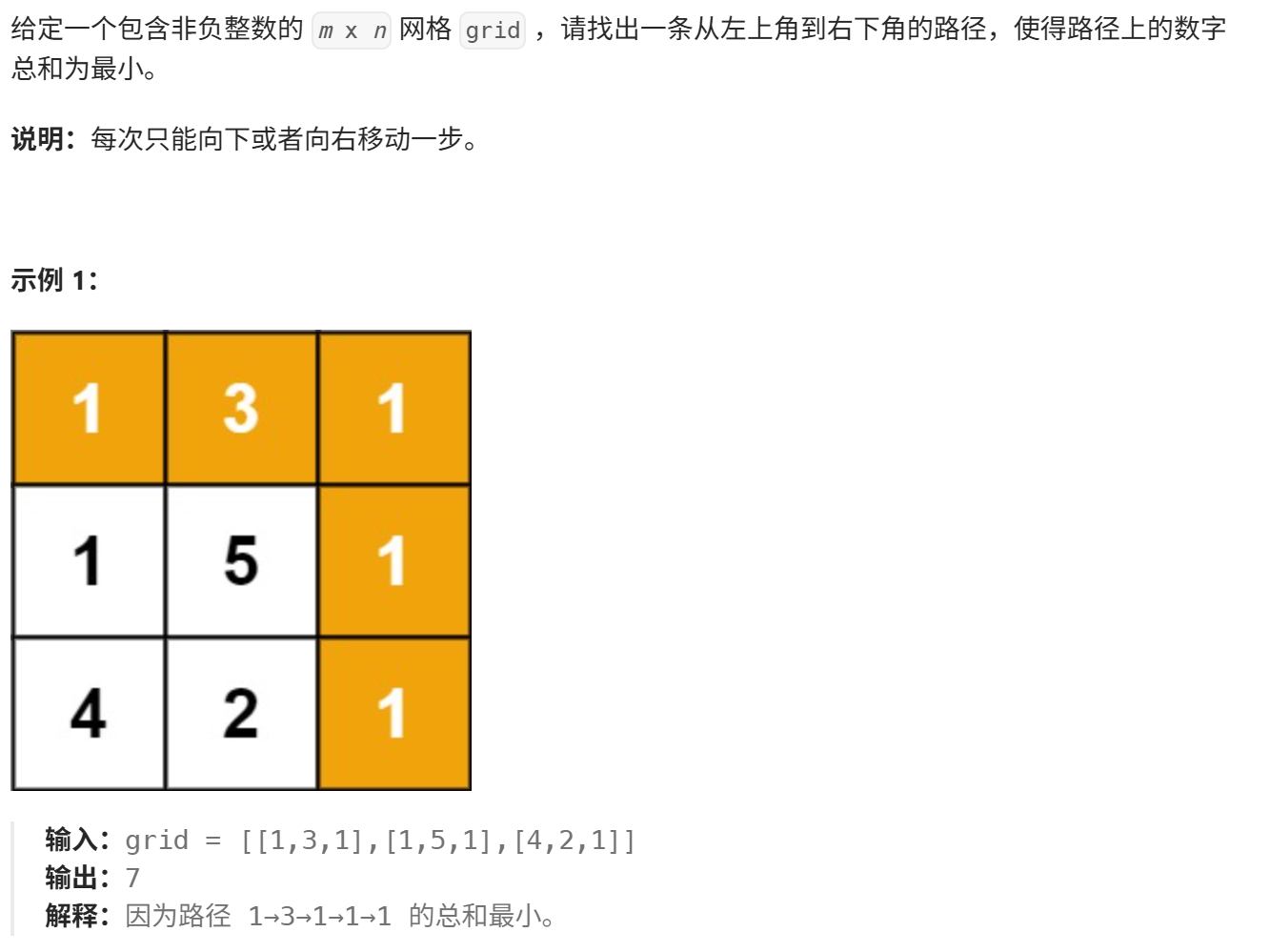
二、解题思路

整体思路

由题意可知，本次的选择基于前面的结果，所以可以使用动态规划来解决这个问题。

具体思路

（1）dpij的含义

dpij的值表示到（i，j）位置的最小路径和。

（2）初始化

由于只能向右和向下移动，所以可以将dp数组的第一列和第一行初始化：

<1>第一行只能由起点持续右移得到，所以dp0col=dp0col-1+grid0col；

<2>第一列只能由起点持续下移得到，所以dprow0=dprow-10+gridrow0;

（3）状态转移方程

中间的位置只能由其上面的位置下移或者左边的位置右移动得到，所以状态转移方程为：

dprowcol=gridrowcol+min(dprow-1col,dprowcol-1);

三、代码实现

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        //动态规划
        int m=grid.size();
        int n=grid[0].size();
        if(m==0||n==0) return 0;
        vector<vector<int>> dp(m,vector<int>(n,0));

        //填写dp数组
        dp[0][0]=grid[0][0];
       //填写第一行
       for(int col=1;col!=n;col++) dp[0][col]=dp[0][col-1]+grid[0][col];
       //填写第一列
       for(int row=1;row!=m;row++) dp[row][0]=dp[row-1][0]+grid[row][0];
       //填写中间位置
       for(int row=1;row!=m;row++)
        for(int col=1;col!=n;col++)
            dp[row][col]=grid[row][col]+min(dp[row-1][col],dp[row][col-1]);

        return dp[m-1][n-1];
    }
};