算法沉淀第二天（Catching the Krug）

引言：

[Catching the Krug](#Catching the Krug)

题意分析

逻辑梳理

代码实现

结语：

引言：

今天是算法沉淀的第二天，开的是CF评级为1300的一道题，这道题用分类讨论就可以解决了，甚至不需要用到算法，那么接下来，话不多说，我们就进入今天的算法讲解--------------------->

Catching the Krug

按照惯例，我们先来看题目

题意分析

题目链接如下Problem - 2152B - Codeforces

不想跳转的可看下图

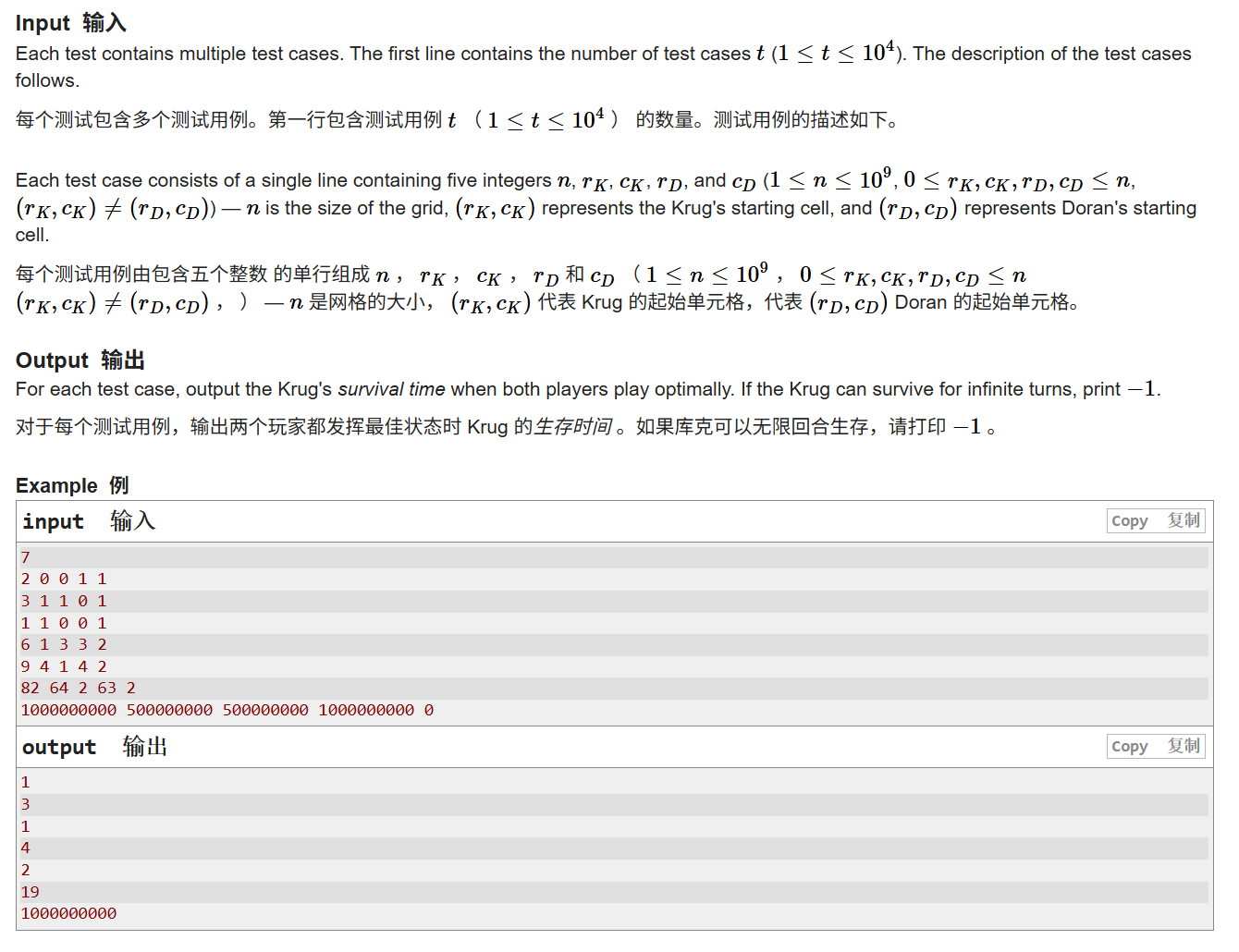
这道题虽然题目描述的很长，其实目的很简单，就是有俩个人，假设分别是A人和B人，然后，A人负责逃跑，B人负责追击，如果B人追不到A人就输出-1，如果B人如果能追到A人就输出最少的追击次数，A和B在同一个格子上就算追击到了

A不想被B追到，所以A会用最优的方式来躲B，然后B想快点追上A，所以B也会用最优的方式来追击A

然后会问你ｔ种情况，每种情况先告诉你Ａ的坐标再告诉你Ｂ的坐标

那Ａ和Ｂ的走法是怎么走的呢，Ａ每次可以横着或者竖着走一格（也可以不走），Ｂ则是每次可以走的位置是他所在的格子的周围一圈（也可以不走），然后，走法是Ａ先走，再Ｂ走，这样轮流走

那么，题目意思讲完了，接下来，就进入逻辑梳理环节咯

逻辑梳理

首先，Ａ只能横着或竖着走，但Ｂ可以斜着走，所以如果Ｂ想要快点追到Ａ，肯定会堵Ａ的路，Ａ最终肯定会被抓到，所以输出－１的情况是不存在的

那么，既然Ａ已经知道自己会被堵，那么Ａ肯定会移动到最远的位置，然后不动，这样才能躲得更久，那么Ａ可以去上下的边界，也可以去左右的边界，那么具体去哪里也要看Ａ与Ｂ的位置关系

那具体怎么移，我们可以通过Ｂ来看，不管Ａ怎么移动，因为Ｂ的可移动性远高于Ａ，所以可以相当于是Ｂ的平推，因为Ｂ可以通过斜着走堵住Ａ的未来路，所以这时候就只会有俩种情况了，一种是Ｂ沿着水平方向平推到边界，另一种是Ｂ沿着竖直方向平推到边界

那么，我们只需要去这俩种情况的最大值就好了，因为Ａ想晚点被抓到，所以Ｂ肯定要走更多的操作次数

那么，情况分析完了，接下来，就进行分类讨论就好啦

我们可以通过Ａ，Ｂ的ｘ轴坐标的差异，分为三种情况，接着再细分，假设Ａ的坐标为（ｘ１，ｙ１），Ｂ的坐标为（ｘ２，ｙ２）

若ｘ１＜ｘ２

这时候，Ａ的位置在Ｂ的左侧，我们可以对Ａ的位置通过ｙ的差距来进行进一步细分

如果ｙ１＞ｙ２

这说明Ａ的位置在Ｂ的左上角，Ａ可以往左走，也可以往上走，那Ｂ追到Ａ的移动次数就是Ｂ到左边界和上边界的俩个值中的较大值

如果ｙ１＞ｙ２

这说明Ａ的位置在Ｂ的左下角，Ａ可以往左走，也可以往下走，那Ｂ追到Ａ的移动次数就是Ｂ到左边界和下边界的俩个值中的较大值

如果ｙ１＝＝ｙ２

这说明Ａ的位置在Ｂ的正左边，这时候Ｂ只要一直往左走就能抓到了，如果Ａ想上下走，Ｂ只要斜着往左压过去就可以了，所以这种情况下的移动次数就是Ｂ到左边界的移动次数

若ｘ１＞ｘ２

这个就跟上面那个同理了，只是算的时候数据会变化

若ｘ１＝＝ｘ２

这个情况就比较特殊了，这个就跟上面ｘ１！＝ｘ２时，但ｙ１＝＝ｙ２一样，只需要算出Ｂ到对应边界的操作次数就好了

那么所有情况就讨论完了，接下来就进入代码实现的环节啦

代码实现

代码的思路逻辑梳理已经讲的很清楚啦，那么接下来，就直接展示ＡＣ码啦

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;

int t;

void solve()
{
	long long n, x1, y1, x2, y2;
	cin >> n >> x1 >> y1 >> x2 >> y2;
	if (x1 < x2)
	{
		if (y1 == y2)
		{
			cout << x2 << endl;
		}
		else if (y1 < y2)
		{
			cout << max(x2, y2) << endl;
		}
		else
		{
			cout << max(x2, n - y2) << endl;
		}
	}
	else if (x1 > x2)
	{
		if (y1 == y2)
		{
			cout << n - x2 << endl;
		}
		else if (y1 < y2)
		{
			cout << max(n - x2, y2) << endl;
		}
		else
		{
			cout << max(n - x2, n - y2) << endl;
		}
	}
	else
	{
		if (y1 < y2)
			cout << y2 << endl;
		else
			cout << n - y2 << endl;
	}
}

int main()
{
	cin >> t;
	while (t--)
	{
		solve();
	}
	return 0;
}

结语：

今日算法讲解到此结束啦，希望对你们有所帮助，谢谢观看，如果觉得不错可以分享给朋友哟。有什么看不懂的可以评论问哦，