本文将从原理、结构到代码实现,全面解析循环神经网络家族,带你理解如何让神经网络拥有"记忆"能力
一、引言:为什么需要循环神经网络?
在深度学习的广阔天地中,我们常常遇到这样的数据:一句话、一段音乐、股票价格走势、传感器读数流...这些序列数据 有一个共同特点:数据点之间存在时间或顺序上的依赖关系。
传统的前馈神经网络(如全连接网络、CNN)在处理这类数据时存在根本性缺陷:它们没有记忆。每次输入都是独立处理的,网络无法利用历史信息来理解当前输入。
举个例子:
-
预测句子"
我在上海长大,所以我会说流利的___"的最后一个词 -
人类能轻松填上"
上海话"或"中文",因为我们记住了关键信息"上海" -
传统神经网络看到"
流利的"时,早已忘记了句子开头的"上海"
循环神经网络(RNN) 的提出,正是为了赋予神经网络"记忆"的能力,使其能够处理序列数据并捕捉时间依赖关系。
二、循环神经网络(RNN)基础
2.1 RNN的核心思想
RNN的核心在于循环连接(Recurrent Connection)。与普通神经网络不同,RNN单元不仅接收当前输入,还接收上一个时间步的"状态",并将当前状态传递给下一个时间步。
这种设计使得RNN能够维护一个"内部状态",该状态理论上可以编码从序列开始到当前时间步的所有历史信息。
2.2 RNN的数学原理
对于一个时间步 t,RNN的计算过程如下:
python
def rnn_cell(x_t, h_prev, W_xh, W_hh, W_hy, b_h, b_y):
# 更新隐藏状态
h_t = tanh(dot(W_xh, x_t) + dot(W_hh, h_prev) + b_h)
# 计算输出
y_t = dot(W_hy, h_t) + b_y
return y_t, h_t数学公式表示:
-
隐藏状态更新 :
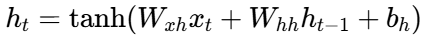
-
输出计算 :
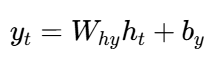
其中:
-
xt:当前时间步的输入
-
ht−1:上一个时间步的隐藏状态(记忆)
-
ht:当前时间步的新隐藏状态
-
yt:当前时间步的输出
-
W∗,b∗:可学习的权重和偏置参数
2.3 RNN的展开计算图
为了更好地理解RNN的工作方式,我们通常将其按时间步展开:
python
时间步1: x₁ → [RNN] → y₁, h₁
时间步2: x₂ → [RNN] → y₂, h₂
时间步3: x₃ → [RNN] → y₃, h₃这种展开显示了一个RNN实际上是在不同时间步共享参数的深层网络。
2.4 RNN的类别与应用场景
根据输入输出的不同组合,RNN主要有以下几种架构:
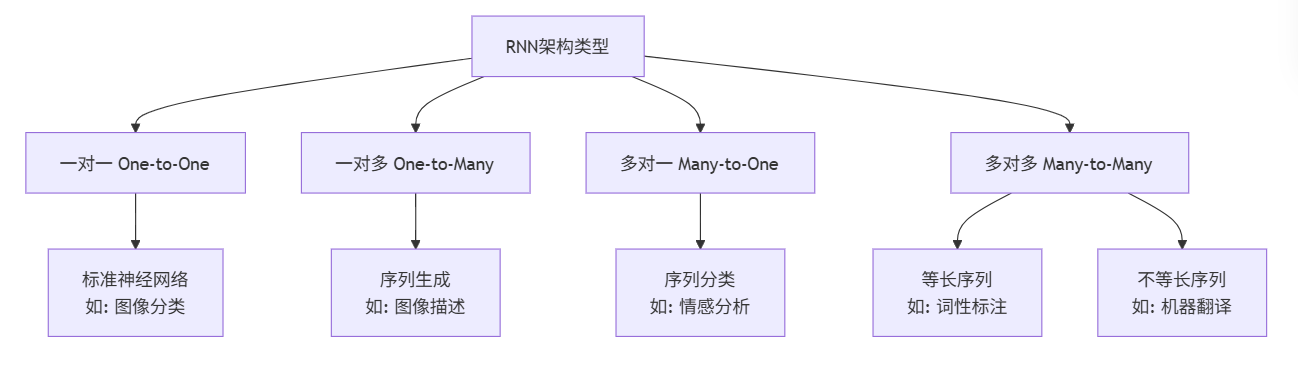
三、RNN的挑战:梯度消失与爆炸问题
3.1 问题的根源
虽然RNN理论上可以处理任意长度的序列,但在实践中训练深度RNN(即处理长序列)会遇到严重问题:梯度消失(Vanishing Gradient) 和梯度爆炸(Exploding Gradient)。
这些问题源于反向传播通过时间(BPTT) 算法。在BPTT中,梯度需要从最终时间步一路传播回序列的起始位置。如果序列很长,梯度需要连续乘以多个权重矩阵。
数学分析:
考虑梯度传播链式法则:
其中每个雅可比矩阵 ∂ht−1∂ht的特征值决定梯度命运:
-
如果特征值 < 1 :梯度指数级缩小 → 梯度消失
-
如果特征值 > 1 :梯度指数级增大 → 梯度爆炸
3.2 问题的影响
梯度消失导致RNN难以学习长期依赖关系。网络更关注近期信息,而难以记住序列早期的关键信息。
举个例子:
在句子"我出生在法国...我能说流利的___"中,RNN可能忘记关键的"法国"信息,从而无法正确预测"法语"。
四、长短期记忆网络(LSTM)
为了解决RNN的长期依赖问题,Hochreiter和Schmidhuber在1997年提出了长短期记忆网络(LSTM)。
4.1 LSTM的核心创新:门控机制
LSTM的关键创新是引入了精密的"门控机制",有选择地控制信息的流动。LSTM有三个核心门控:
-
遗忘门(Forget Gate):决定从记忆单元中丢弃哪些信息
-
输入门(Input Gate):决定将哪些新信息存入记忆单元
-
输出门(Output Gate):决定基于当前记忆单元输出什么信息
4.2 LSTM的详细结构
LSTM比标准RNN复杂得多,但正是这种复杂性使其能够有效学习长期依赖。下图展示了LSTM单元在一个时间步内的完整计算流程:
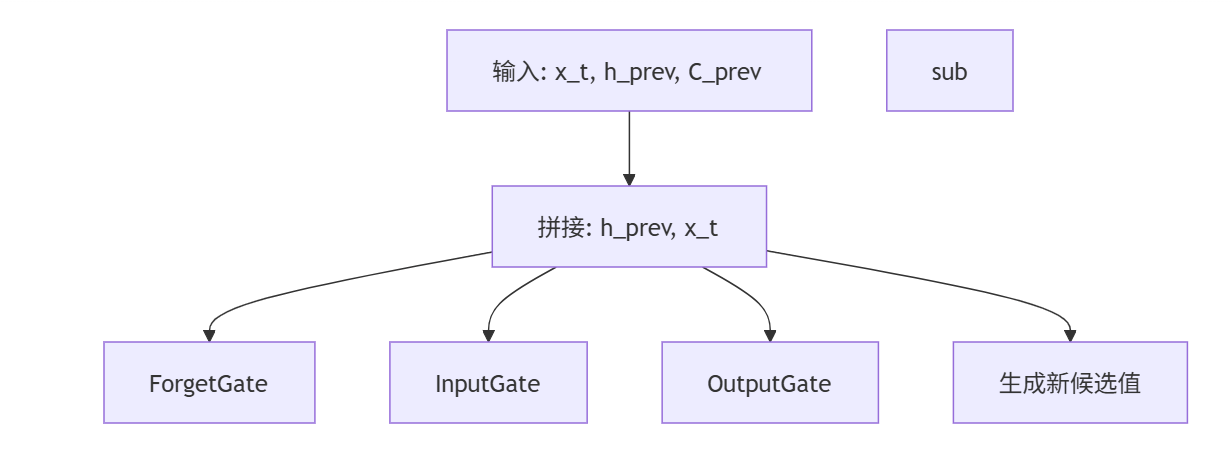
4.3 LSTM的数学公式
LSTM在每个时间步执行以下计算:
python
# LSTM前向传播伪代码
def lstm_cell(x_t, h_prev, C_prev, parameters):
# 1. 计算三个门控
forget_gate = sigmoid(dot(W_f, [h_prev, x_t]) + b_f)
input_gate = sigmoid(dot(W_i, [h_prev, x_t]) + b_i)
output_gate = sigmoid(dot(W_o, [h_prev, x_t]) + b_o)
# 2. 生成候选记忆内容
C_tilde = tanh(dot(W_C, [h_prev, x_t]) + b_C)
# 3. 更新细胞状态(长期记忆)
C_t = forget_gate * C_prev + input_gate * C_tilde
# 4. 计算新隐藏状态(短期记忆/输出)
h_t = output_gate * tanh(C_t)
# 5. 计算输出(可选,通常h_t就是输出)
y_t = dot(W_y, h_t) + b_y
return y_t, h_t, C_t数学公式:
-
遗忘门:ft=σ(Wf⋅[ht−1,xt]+bf)
-
输入门:it=σ(Wi⋅[ht−1,xt]+bi)
-
输出门:ot=σ(Wo⋅[ht−1,xt]+bo)
-
候选记忆:C~t=tanh(WC⋅[ht−1,xt]+bC)
-
细胞状态更新:Ct=ft⊙Ct−1+it⊙C~t
-
隐藏状态更新:ht=ot⊙tanh(Ct)
4.4 LSTM如何解决梯度消失问题?
LSTM通过细胞状态 和门控机制巧妙解决了梯度消失问题:
-
细胞状态的高速公路 :细胞状态 Ct的更新主要是加法操作(Ct=ft⊙Ct−1+it⊙C~t),而不是乘法。在反向传播时,梯度可以几乎无损耗地通过这条"高速公路"流动。
-
门控的精细调控:三个门控学习何时记住、何时忘记、何时输出,使得网络能够自主选择保持哪些梯度信息。
五、门控循环单元(GRU)
5.1 GRU:LSTM的简化版本
GRU是Cho等人在2014年提出的LSTM变体,旨在在保持LSTM效果的同时简化结构。
主要简化:
-
将遗忘门和输入门合并为更新门(Update Gate)
-
将细胞状态和隐藏状态合并为一个隐藏状态
-
参数减少约1/3,训练更快
5.2 GRU的数学公式
python
# GRU前向传播伪代码
def gru_cell(x_t, h_prev, parameters):
# 1. 计算两个门控
update_gate = sigmoid(dot(W_z, [h_prev, x_t]) + b_z)
reset_gate = sigmoid(dot(W_r, [h_prev, x_t]) + b_r)
# 2. 计算候选隐藏状态
h_tilde = tanh(dot(W_h, [reset_gate * h_prev, x_t]) + b_h)
# 3. 更新隐藏状态
h_t = (1 - update_gate) * h_prev + update_gate * h_tilde
return h_t, h_t # 通常隐藏状态就是输出数学公式:
-
更新门:zt=σ(Wz⋅[ht−1,xt]+bz)
-
重置门:rt=σ(Wr⋅[ht−1,xt]+br)
-
候选状态:h~t=tanh(Wh⋅[rt⊙ht−1,xt]+bh)
-
隐藏状态更新:ht=(1−zt)⊙ht−1+zt⊙h~t
六、PyTorch实战:文本生成示例
下面我们使用PyTorch实现一个基于LSTM的文本生成模型。
6.1 数据准备与预处理
python
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
from collections import Counter
class TextProcessor:
"""文本预处理类"""
def __init__(self, text, seq_length=30):
self.text = text
self.seq_length = seq_length
self.chars = sorted(list(set(text)))
self.vocab_size = len(self.chars)
self.char_to_idx = {ch: i for i, ch in enumerate(self.chars)}
self.idx_to_char = {i: ch for i, ch in enumerate(self.chars)}
def create_sequences(self):
"""创建训练序列"""
sequences = []
next_chars = []
for i in range(0, len(self.text) - self.seq_length):
seq = self.text[i:i + self.seq_length]
next_char = self.text[i + self.seq_length]
sequences.append([self.char_to_idx[ch] for ch in seq])
next_chars.append(self.char_to_idx[next_char])
return torch.tensor(sequences), torch.tensor(next_chars)
# 示例文本(实际应用中使用更大语料库)
sample_text = """
在深度学习领域,循环神经网络是一种重要的架构。
它能够处理序列数据,如文本、语音和时间序列。
LSTM和GRU是RNN的变体,解决了梯度消失问题。
"""
processor = TextProcessor(sample_text)
X, y = processor.create_sequences()
print(f"数据形状: {X.shape}, 标签形状: {y.shape}")6.2 LSTM模型实现
python
class TextLSTM(nn.Module):
"""基于LSTM的文本生成模型"""
def __init__(self, vocab_size, embedding_dim=128, hidden_dim=256, n_layers=2, dropout=0.2):
super().__init__()
self.vocab_size = vocab_size
self.hidden_dim = hidden_dim
self.n_layers = n_layers
# 词嵌入层
self.embedding = nn.Embedding(vocab_size, embedding_dim)
# LSTM层
self.lstm = nn.LSTM(embedding_dim, hidden_dim, n_layers,
dropout=dropout, batch_first=True)
# Dropout正则化
self.dropout = nn.Dropout(dropout)
# 输出层
self.fc = nn.Linear(hidden_dim, vocab_size)
def forward(self, x, hidden=None):
# 词嵌入
x = self.embedding(x) # [batch, seq_len] -> [batch, seq_len, emb_dim]
# LSTM前向传播
lstm_out, hidden = self.lstm(x, hidden) # lstm_out: [batch, seq_len, hidden_dim]
# 只取最后一个时间步的输出
last_output = lstm_out[:, -1, :]
# 全连接层
output = self.fc(self.dropout(last_output))
return output, hidden
def init_hidden(self, batch_size, device):
"""初始化隐藏状态"""
weight = next(self.parameters())
return (weight.new_zeros(self.n_layers, batch_size, self.hidden_dim).to(device),
weight.new_zeros(self.n_layers, batch_size, self.hidden_dim).to(device))
# 模型初始化
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = TextLSTM(processor.vocab_size).to(device)
print(f"模型参数量: {sum(p.numel() for p in model.parameters()):,}")6.3 训练循环
python
def train_model(model, X, y, epochs=1000, lr=0.001):
"""训练模型"""
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=lr)
# 将数据移动到设备
X, y = X.to(device), y.to(device)
losses = []
model.train()
for epoch in range(epochs):
# 初始化隐藏状态
hidden = model.init_hidden(X.size(0), device)
# 前向传播
output, hidden = model(X, hidden)
loss = criterion(output, y)
# 反向传播
optimizer.zero_grad()
loss.backward()
# 梯度裁剪,防止梯度爆炸
torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=5.0)
optimizer.step()
losses.append(loss.item())
if epoch % 100 == 0:
print(f'Epoch {epoch:4d}/{epochs}, Loss: {loss.item():.4f}')
return losses
# 训练模型(小规模演示)
losses = train_model(model, X, y, epochs=500)6.4 文本生成
python
def generate_text(model, processor, start_text, length=100, temperature=0.8):
"""使用训练好的模型生成文本"""
model.eval()
generated = start_text.lower()
with torch.no_grad():
# 初始化输入序列
if len(generated) < processor.seq_length:
# 填充序列
current_seq = generated + ' ' * (processor.seq_length - len(generated))
else:
current_seq = generated[-processor.seq_length:]
for _ in range(length):
# 将当前序列转换为张量
input_seq = torch.tensor([
[processor.char_to_idx.get(ch, 0) for ch in current_seq]
]).to(device)
# 前向传播
hidden = model.init_hidden(1, device)
output, hidden = model(input_seq, hidden)
# 应用温度采样
output = output / temperature
probabilities = torch.softmax(output, dim=-1)
# 采样下一个字符
next_char_idx = torch.multinomial(probabilities, 1).item()
next_char = processor.idx_to_char[next_char_idx]
generated += next_char
current_seq = current_seq[1:] + next_char # 滑动窗口
return generated
# 生成文本示例
generated_text = generate_text(model, processor, "循环神经网络", length=50)
print(f"生成的文本: {generated_text}")七、现代发展与总结
7.1 RNN家族的比较
| 模型 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|
| 标准RNN | 结构简单,计算量小 | 梯度消失,难以学习长期依赖 | 简单序列任务 |
| LSTM | 能学习长期依赖,功能强大 | 参数多,训练慢 | 复杂长序列任务 |
| GRU | 参数少,训练快,效果接近LSTM | 极长序列可能不如LSTM | 大多数序列任务 |
7.2 现代替代方案:Transformer
虽然LSTM/GRU在序列建模中取得了巨大成功,但近年来Transformer架构已成为新的主流,特别是在自然语言处理领域。
Transformer的优势:
-
并行计算:摆脱序列顺序限制,大幅提升训练速度
-
自注意力机制:直接捕捉长距离依赖关系
-
可扩展性:适合构建超大规模模型(如GPT、BERT)
然而,RNN/LSTM/GRU在以下场景仍有其价值:
-
资源受限的边缘计算设备
-
需要严格时间顺序的实时应用
-
小规模数据集上的。