【Open3D】Ch.3：顶点法向量估计 | Python

顶点法向量估计

• 前言
• [1. 官方文档](#1. 官方文档)
• [2. 基础概念简介](#2. 基础概念简介)
• • 顶点法向量估计
  • PCA
  • 协方差矩阵
  • KDTreeSearchParamHybrid
  • KDTree
• [3. 例程拆解和复现](#3. 例程拆解和复现)
• • [3.1 先跑例程](#3.1 先跑例程)
  • [3.2 例程拆解](#3.2 例程拆解)
• [4. 补充：访问顶点法向量](#4. 补充：访问顶点法向量)
• 后记
• 参考资料

前言

点云光照渲染、表面分割、曲面重建等场景，都离不开顶点法向量估计。

在Ch.3聚焦借助Open3D封装好的API进行顶点法向量估计。

本文仍为学习笔记，非系统教程，建议根据需求跳转到对应部分阅读。

文末参考资料我放了链接，可直接跳转到相关网站。

1. 官方文档

点云的另一项基本操作是点法线估计。按下 N 键可查看点法线。减号（-）和加号（+）键可用于控制法线的长度。

estimate_normals为每个点计算法线。该函数找到相邻的点，然后使用协方差分析来计算相邻点的主轴。

该函数接受一个 KDTreeSearchParamHybrid 类的实例作为参数。两个关键参数 radius = 0.1 和 max_nn = 30 分别指定搜索半径和最大近邻数和。它具备 10 厘米的搜索半径，并且为节省计算时间，最多只考虑 30 个邻域。

注意：

协方差分析算法会生成两个相反的方向作为法向量候选。在不了解几何结构全局信息的情况下，这两个方向都可能是正确的，这被称为法向量定向问题。如果原始法向量存在，Open3D 会尝试将法向量定向为与原始法向量对齐；否则，Open3D 会随机猜测法向量方向。如果需要关注法向量的定向，需要调用进一步的定向函数，例如 orient_normals_to_align_with_direction（将法向量对齐到指定方向）和 orient_normals_towards_camera_location（将法向量朝向相机位置）。

2. 基础概念简介

（在此只对概念做简单的介绍，想要深入了解的可以参考文末的参考文献）

顶点法向量估计

很多三维任务，例如光照渲染、三维重建、特征提取与匹配、物理模拟都需要用到法向信息，但是原始的点云数据往往不带法向数据，所以需要通过估计获取。

法向（normal），也叫法线，是垂直于曲面上某一点切平面的向量。

顶点法向即该顶点所在表面或者局部集合结构的法向。对于点云数据，只有离散的点，通过算法计算领域点的方式来估计顶点的法向。

顶点法向估计主要有以下几步：

1. 确定目标点
2. 对目标点用KDTree 搜索算法 找到临近的几个点
3. 进行PCA分析
4. 到特征值最小的特征向量为法向量

PCA

PCA即主成分分析，是一种降维方法，可在降低数据维度的同时，尽可能保留数据的关键信息，常用于数据压缩、特征提取等任务。

协方差矩阵

协方差矩阵是描述多维数据各维度间线性关系与离散程度的矩阵，能体现维度间的相关性和单个维度的离散性。

KDTreeSearchParamHybrid

KDTreeSearchParamHybrid是 Open3D 中用于邻域搜索的混合策略，在点云的 KDTree 结构中，为每个点搜索 距离不超过radius且数量不超过max_nn 的邻域点，平衡搜索范围与计算效率。

KDTree

KDTree 是一种适用于多维空间的树形数据结构，通过在不同维度上递归划分空间构建二叉树，能高效实现近邻搜索和范围查询，常用于点云处理、机器学习等场景中快速查找数据点的邻居。

3. 例程拆解和复现

3.1 先跑例程

import open3d as o3d
import numpy as np

# ch.1 里的点云读取
ply_point_cloud = o3d.data.PLYPointCloud()
pcd = o3d.io.read_point_cloud(ply_point_cloud.path)
print(pcd)
print(np.asarray(pcd.points))

# ch.2里的体素下采样
print("Downsample the point cloud with a voxel of 0.05")
downpcd = pcd.voxel_down_sample(voxel_size=0.05)

# 这块是新增的法向量估计
print("Recompute the normal of the downsampled point cloud")
downpcd.estimate_normals(
    search_param=o3d.geometry.KDTreeSearchParamHybrid(radius=0.1, max_nn=30))

# 显示
o3d.visualization.draw_geometries([downpcd],
                                  zoom=0.3412,
                                  front=[0.4257, -0.2125, -0.8795],
                                  lookat=[2.6172, 2.0475, 1.532],
                                  up=[-0.0694, -0.9768, 0.2024],
                                  point_show_normal=True)

运行后，终端会输出点云的基本信息，同时弹出可视化窗口，如下：

发现每一个点都有一根线指出，这就是该点的法向量，表示点的朝向。

3.2 例程拆解

在例程中法向量估计分为两步骤：

1. 配置邻域搜索规则
2. 执行法向量计算

底层是如何操作的，现阶段可以不用深究，直接调用Open3D给的API就可以达到我们的目标。

下面介绍一下我们要调用的关键API：

o3d.geometry.KDTreeSearchParamHybrid(radius, max_nn)

这是 Open3D 用于定义 "如何找邻域点" 的类。

通过两个参数平衡搜索范围与计算效率：

1. radius：邻域搜索的半径。
2. max_nn：每个点最多选多少个邻域点。

estimate_normals(search_param)

这是 PointCloud 对象的方法，作用是为点云中的每个点计算法向量。

只需把上面配置好的 "邻域搜索规则"，即 KDTreeSearchParamHybrid 生成的 search_param传入，它会自动完成 找邻域点 → 拟合局部平面 → 求解法向量 的全流程。

还有一点要补充的是 o3d.visualization.draw_geometries 的参数，如下图是我们在ch.1中已经介绍过的它的关键参数。

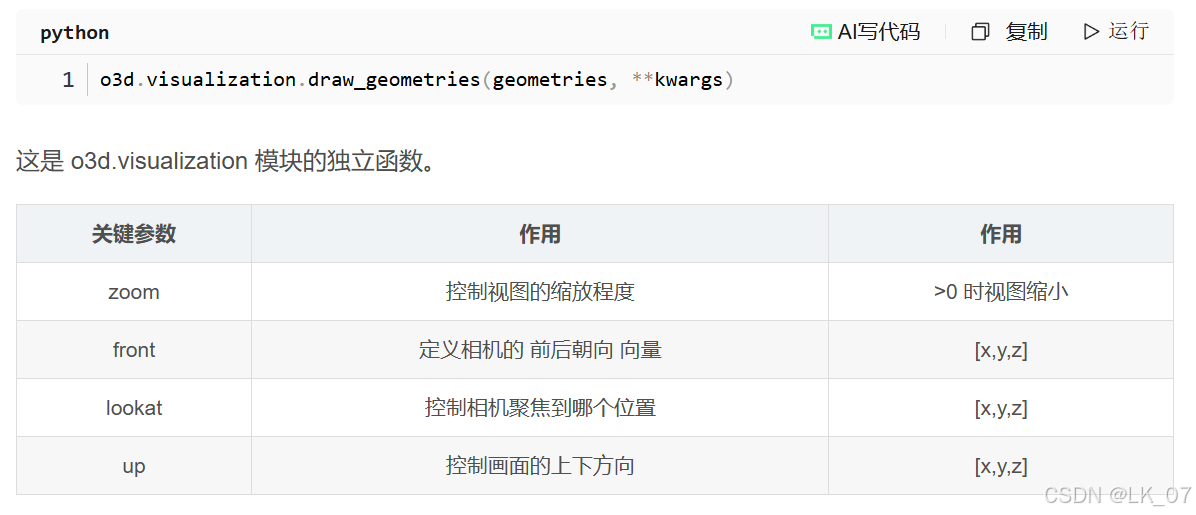
通过观察例程我们发现，在调用 o3d.visualization.draw_geometries 时多出来一个参数 point_show_normal 。

它用于控制是否显示点云的法线 。为True时，显示法线；为False时，不显示。

运行下方代码，将得到例程的结果

import open3d as o3d
import numpy as np

ply_point_cloud = o3d.data.PLYPointCloud()
pcd = o3d.io.read_point_cloud(ply_point_cloud.path)
print(pcd)
print(np.asarray(pcd.points))

print("Downsample the point cloud with a voxel of 0.05")
downpcd = pcd.voxel_down_sample(voxel_size = 0.05)

print("Recompute the normal of the downsampled point cloud")
radius = 0.1
max_nn = 30
downpcd.estimate_normals(
    search_param=o3d.geometry.KDTreeSearchParamHybrid(radius, max_nn))

o3d.visualization.draw_geometries([downpcd],
                                  zoom=0.3412,
                                  front=[0.4257, -0.2125, -0.8795],
                                  lookat=[2.6172, 2.0475, 1.532],
                                  up=[-0.0694, -0.9768, 0.2024],
                                  point_show_normal=True)

我们可以尝试更改参数，看看实际的变化：

radius = 0.1
max_nn = 3

radius = 1
max_nn = 100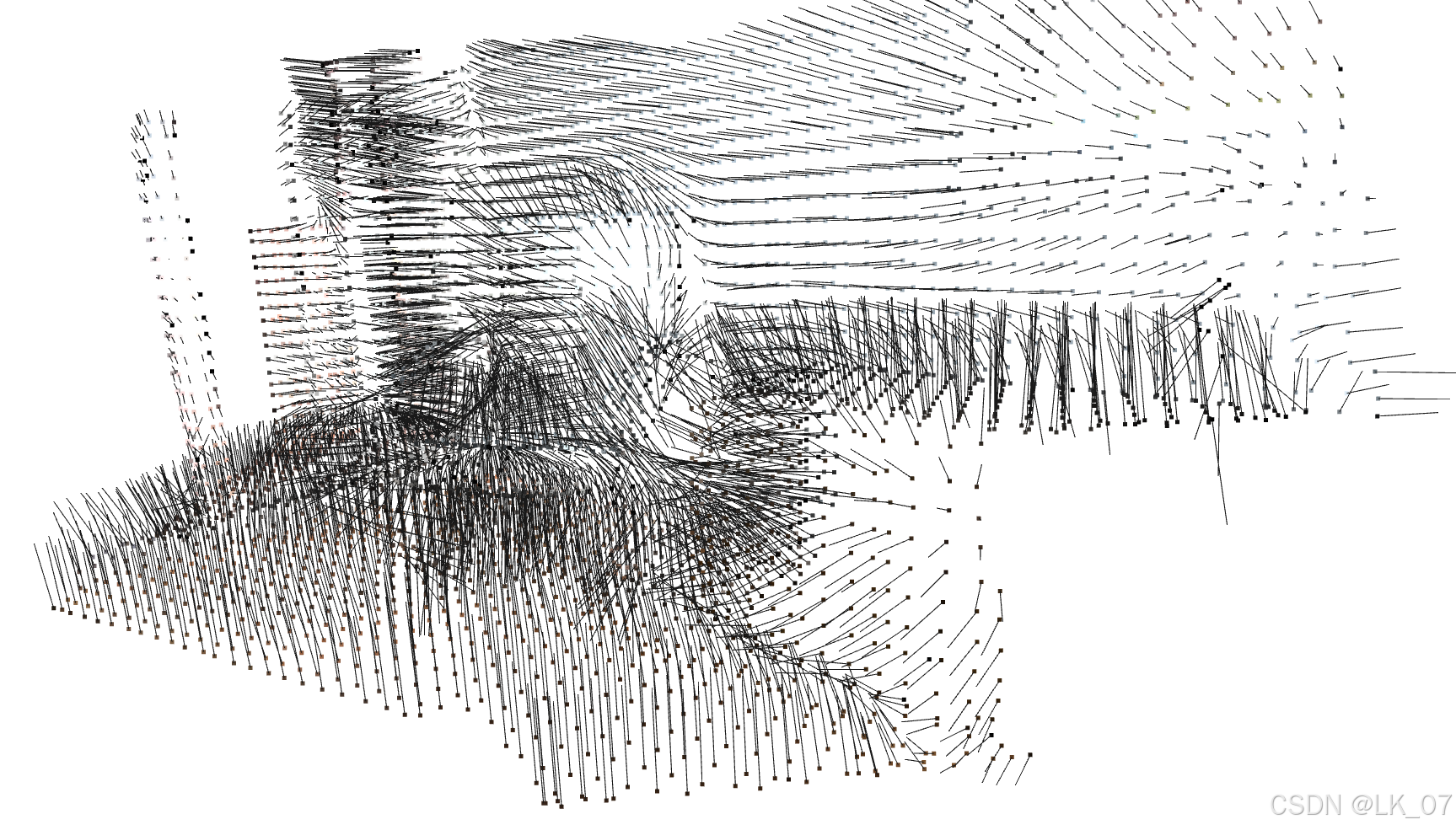

实际发现，若邻域范围或最大邻点数太小时，法向量会因 局部信息不足 而不稳定，局部性过强；只有当参数足够大，能覆盖足够多的邻点，法向量才能更准确反映表面整体趋势。

但是范围和点数也不是越大越好，像是官方文档里说的还需要考虑时间的问题，当你的数据量非常之大时，选取合适的范围和点数也是很重要的。

4. 补充：访问顶点法向量

在完成法向量估计后，我们可以直接访问点云中每个点的法向量数据，用于后续分析或自定义处理。

直接访问已完成法向量估计的 PointCloud 对象的 normals 属性就可以。

print(downpcd.normals[0])

像是上面的代码打印了第一个点的法向量数据，输出如下，是一个三维坐标的形式。

0.85641574 0.01693013 -0.51600915

---

后记

感谢你能看到这，希望我的笔记能对你有帮助。

文章相关代码我已经放到了我的Gitee里了，有需要的可以自取Open3D点云笔记。

我还在学习阶段，个人能力有限，文章难免有疏漏和差错，望指出。

上一篇【Open3D】Ch.2：点云体素下采样 | Python

下一篇写 裁剪点云数据。

参考资料

1. 顶点法向估计
   《三维点云处理》学习笔记（1）：平面法向量估计
   补充资料（可做了解）：
   网格顶点法向的计算（基于面平均方法）
   网格顶点方向的计算（一种新的面积加权方法）
   国内首次 | 山东大学交叉研究中心全新点云法向估计算法荣获SIGGRAPH最佳论文奖！
2. PCA
   关于协方差和协方差矩阵 以及PCA
3. KD-Tree
   KD-Tree原理详解
   详解KDTree