华为AI岗 -- 笔试（一）

华为牛客网

AI题牛客网

目录

一、华为代码题

[1. DBSCAN 聚类 （10.10）](#1. DBSCAN 聚类 （10.10）)

[2. 实现Masked Multi-Head Self-Attention （9.28）](#2. 实现Masked Multi-Head Self-Attention （9.28）)

二、代码题读入格式

三、选择题

---

一、华为代码题

1. DBSCAN 聚类 （10.10）

• 任务: 用DBSCAN在二维或三维实数坐标上做聚类，输出"簇的数量"和"噪声点数量"。
• 定义: 距离为欧氏距离；某点的邻域半径为eps；若该点邻域内样本数（含自身）≥ min_samples，则为核心点 ；从未访问核心点出发，按邻域可达关系扩展一个簇；不被任何簇吸收的点视为噪声

import math
 
def euclidean_distance(a, b):
    return math.sqrt(sum((x - y) ** 2 for x, y in zip(a, b)))
 
def main():
    eps, min_samples, x = input().split()
    eps = float(eps)
    min_samples = int(min_samples)
    x = int(x)
     
    points = [] # 读入点集
    for _ in range(x):
        coords = list(map(float, input().split()))
        points.append(coords)
     
    cluster_count, noise_count = dbscan(points, eps, min_samples)
    print(cluster_count, noise_count)
 
if __name__ == "__main__":
    main()

思路 -- 对每个未访问点：

• 找它的邻域（距离 ≤ eps）

• 如果邻域内点数 < min_samples，标记为噪声（但噪声可能后来被重新归类到簇中，如果它是某个核心点的邻域点）

• 如果邻域内点数 ≥ min_samples，则它是核心点，以它开始扩展新簇：

  • 把邻域内所有点加入该簇

  • 对邻域内每一个未访问点，递归检查是否为核心点 ，如果是，把它的邻域也加入簇

region_query 邻域点， 可用来判断是否为核心点。

seeds 代表待用来扩展的点。初始为当前核心点 p_idx 的邻域。

while循环 每次用seeds的头 q_idx 扩展未被访问过的邻域点q：

若 q 是核心点，根据"邻域可达" 把 q 的邻域未访问的点也加入 seed。

操作完后，对刚刚的头 q_idx，如果之前没被标记过标记为 p_idx。

def dbscan(points, eps, min_samples):
    n = len(points)
    visited = [False] * n
    cluster_id = [-1] * n  # -1 表示未分类或噪声
    clusters = []
     
    def region_query(p_idx):
        # 返回邻域内的点的索引列表
        neighbors = []
        for i in range(n):
            if euclidean_distance(points[p_idx], points[i]) <= eps:
                neighbors.append(i)
        return neighbors
     
    def expand_cluster(p_idx, cluster_label):
        # 从核心点 p_idx 扩展簇
        cluster_points = [p_idx]
        visited[p_idx] = True
        cluster_id[p_idx] = cluster_label
         
        # 种子集合
        seeds = region_query(p_idx)
        seeds.remove(p_idx)  # 自己已经处理过
         
        while seeds:
            q_idx = seeds.pop(0)
            if not visited[q_idx]:
                visited[q_idx] = True
                q_neighbors = region_query(q_idx)
                if len(q_neighbors) >= min_samples:
                    # q 也是核心点，将其邻域中未访问的加入 seeds
                    for n_idx in q_neighbors:
                        if not visited[n_idx] and n_idx not in seeds:
                            seeds.append(n_idx)
            if cluster_id[q_idx] == -1:
                cluster_id[q_idx] = cluster_label
                cluster_points.append(q_idx)
        clusters.append(cluster_points)
     
    label = 0
    for i in range(n):
        if not visited[i]:
            neighbors = region_query(i)
            if len(neighbors) < min_samples:
                # 标记为噪声（可能之后被核心点拉入簇）
                cluster_id[i] = -1  # 噪声
            else:
                # 核心点，开始扩展簇
                expand_cluster(i, label)
                label += 1
     
    # 统计噪声点：最终 cluster_id 仍为 -1 的点
    noise_count = sum(1 for cid in cluster_id if cid == -1)
    cluster_count = label  # label 是已分配的簇数
     
    return cluster_count, noise_count

2. 实现Masked Multi-Head Self-Attention （9.28）

给定批量序列表示 X（形状：[batch, seq, d_model]）与权重矩阵 W_Q、W_K、W_V、W_O（均为 d_model×d_model），实现 Masked Multi-Head Self-Attention。

将最后一维按头数 num_heads 均分 ，每头维度 d_k = d_model / num_heads。

计算步骤：

1. Q = X @ W_Q，K = X @ W_K，V = X @ W_V。

2. 将 Q、K、V reshape 为 [batch, num_heads, seq, d_k] 。

3. 计算注意力分数 scores = (Q @ K^T) / sqrt(d_k)，其中 K^T 表示每头在最后两维做转置；乘法得到得到 [batch, num_heads, seq, seq]。

4. 使用下三角因果掩码 （只能看见当前及更早位置）：掩掉上三角元素 （置为一个很小的负数 ）。

5. 在最后一维做 softmax 得到权重，注意数值稳定性 （减去每行最大值 再做 exp）。

6. attention = softmax @ V（形状 [batch, num_heads, seq, d_k]）。

7. 拼回 [batch, seq, d_model] 后，再右乘 W_O。

输出保留两位小数，结果需转换为 Python List。

import math
import numpy as np

def softmax(x, axis=-1):
    # 数值稳定 softmax
    x_max = x.max(axis=axis, keepdims=True)
    e_x = np.exp(x - x_max)
    return e_x / e_x.sum(axis=axis, keepdims=True)


def main():

    # 输入格式 分号分割
    parts = data_str.split(';')
    num_heads = int(parts[0].strip())
    X = eval(parts[1].strip())
    W_Q = eval(parts[2].strip())
    W_K = eval(parts[3].strip())
    W_V = eval(parts[4].strip())
    W_O = eval(parts[5].strip())
    
    result = masked_multi_head_attention(num_heads, X, W_Q, W_K, W_V, W_O)
    print(result)

if __name__ == "__main__":
    main()

按题目要求进行 多头结构，上三角 mask 为负无穷，再尺度变回来

def masked_multi_head_attention(num_heads, X, W_Q, W_K, W_V, W_O):
    X = np.array(X, dtype=np.float32)
    W_Q = np.array(W_Q, dtype=np.float32)
    W_K = np.array(W_K, dtype=np.float32)
    W_V = np.array(W_V, dtype=np.float32)
    W_O = np.array(W_O, dtype=np.float32)
    
    batch, seq_len, d_model = X.shape
    d_k = d_model // num_heads
    
    # 1) Q, K, V
    Q = X @ W_Q  # [batch, seq_len, d_model]
    K = X @ W_K
    V = X @ W_V
    
    # 2) reshape to multi-head
    Q = Q.reshape(batch, seq_len, num_heads, d_k).transpose(0, 2, 1, 3)  # [batch, num_heads, seq_len, d_k]
    K = K.reshape(batch, seq_len, num_heads, d_k).transpose(0, 2, 1, 3)
    V = V.reshape(batch, seq_len, num_heads, d_k).transpose(0, 2, 1, 3)
    
    # 3) scores
    scores = Q @ K.transpose(0, 1, 3, 2)  # [batch, num_heads, seq_len, seq_len]
    scores /= math.sqrt(d_k)
    
    # 4) causal mask
    mask = np.triu(np.ones((seq_len, seq_len), dtype=np.bool_), k=1)  # 上三角（不含对角线）为 True
    scores = scores + (mask * -1e9)  # 上三角置为 -1e9
    
    # 5) softmax
    attn_weights = softmax(scores, axis=-1)  # [batch, num_heads, seq_len, seq_len]
    
    # 6) attention output
    attention = attn_weights @ V  # [batch, num_heads, seq_len, d_k]
    
    # 7) concat heads
    attention = attention.transpose(0, 2, 1, 3).reshape(batch, seq_len, d_model)  # [batch, seq_len, d_model]
    
    # 8) output projection
    output = attention @ W_O  # [batch, seq_len, d_model]
    
    # 保留两位小数
    output_rounded = np.round(output, 2)
    
    return output_rounded.tolist()

比较奇怪的是，样例这样全是整数的情况，要求保留两位小数，numpy删除了后面多余的0.

（所以需要重写输出格式）

二、代码题读入格式

# 读取单行字符串/整数
s = input().strip()
n = int(input().strip())


# 一行整数数列
arr = list(map(int, input().split()))


# 读取多行字符串

n = int(input().strip())
strings = []
for _ in range(n):
    strings.append(input().strip())


# 读取二维整数列表
n, m = map(int, input().split()) # 两个整数
matrix = []
for _ in range(n):
    row = list(map(int, input().split()))
    matrix.append(row)
'''
3 4
1 2 3 4
5 6 7 8
9 10 11 12
'''


# 读带[] 的列表格式使用 eval
matrix = eval(input())
matrix = np.array(eval(input()))
# 输入: [[1, 2, 3], [4, 5, 6], [7, 8, 9]]


# 保留小数控制格式
print(f"π的值: {math.pi:.2f}")

三、选择题

1.在大型语言模型的三阶段训练流程中，哪一个阶段的主要目标是让只会"续写"文本的基座模型变为能理解并遵循人类指令格式的"对话助手"？

A 预训练 (Pre-training)

B 有监督微调 (Supervised Fine-Tuning, SFT)

C 奖励模型训练 (Reward Model Training)

D 基于人类反馈的强化学习 (RLHF)

解析：B

1. 预训练 (Pre-training)

   使用海量文本训练模型，获得语言建模能力（即"续写"能力），但此时模型并不懂得人类指令或对话格式。

2. 有监督微调 (SFT)

   使用高质量的指令-回答对数据，让模型学会遵循指令、进行对话。这直接让模型从"续写文本"变成"对话助手"。

3. 奖励模型训练 (RM Training)

   训练一个打分模型，用于评估生成结果的质量，为 RLHF 阶段提供奖励信号。

4. 基于人类反馈的强化学习 (RLHF)

   利用 RM 对模型输出进行评分，通过强化学习进一步优化模型，使其输出更符合人类偏好。

题目问的是主要目标 是让"续写"模型变为"对话助手"的阶段，这个转变主要发生在 SFT 阶段，因为 SFT 直接教会模型指令遵循和对话格式。

3. 对于 3×224×224 输入，卷积核 7×7、stride=2、padding=3、输出通道64，输出特征图的空间尺寸为（ ）

对于每个维度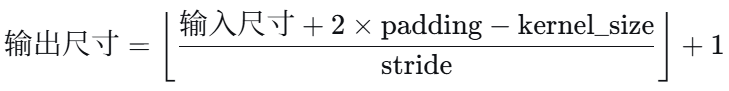

(224+2*3-7) / 2 +1 所以为 112*112

4. 连续掷一枚均匀硬币，首次出现"正反"序列 （一次正面后立刻反面）所需的期望掷币次数为（ ）

定义 初态，中间态，结束态，进行转化。

• E：从初始状态（没有前置投掷）开始，到出现"正反"所需的期望次数。

• EH​：在刚刚掷出一个 H（正面） 的情况下，到出现"正反"所需的期望次数

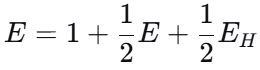扔到反是E ；扔到正是 EH

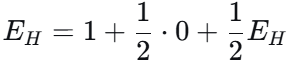扔到反直接结束，扔到正还需要 EH次

5. 在 Stacking 集成学习中：

• 第一层 ：多个基模型对训练数据进行预测（通常用交叉验证方式得到 out-of-fold 预测值）。

• 第二层 （Meta-Model / 元模型 ）：将第一层基模型的预测结果作为输入特征 ，学习如何最优地组合这些预测，以得到最终预测。

因此，第二层模型的作用是 学习基模型预测的组合方式，而不是简单加权平均（那是加权投票或 Blending 的做法），也不是优化基模型的参数（基模型参数训练在第一层已完成），也不是单纯的特征组合（它学习的是组合权重或更复杂的映射关系）。

特性	Tokenizer	Embedding
输入	原始文本字符串	Token ID（整数）
输出	Token ID 序列	向量序列（浮点数）
是否可训练	一般固定（无参数）	可训练（有参数）
作用阶段	数据预处理 / 模型输入前	模型的第一层
主要目标	分割文本、建立词表	将符号转为数值表示、捕获语义

7.欠定 线性方程 y = A x（A 为行满秩胖矩阵），在解集中二范数最小的解为（ ）

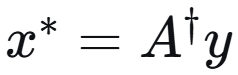伪逆

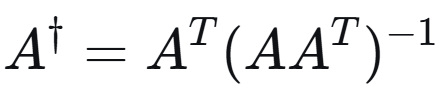
8. 为缓解深层网络的梯度消失，以下激活函数更有效的是（）。

A Softmax B Sigmoid C Tanh D ReLU

A Softmax

主要用于多类分类的输出层，将输出转化为概率分布，并不是隐藏层的激活函数，对梯度消失的缓解无直接作用。

B Sigmoid

输出范围 (0, 1)，导数最大 0.25，在饱和区接近 0，梯度消失问题严重。

C Tanh

输出范围 (-1, 1)，导数范围 (0, 1]，在饱和区梯度会接近 0 ，虽然比 Sigmoid 的梯度更大一些（因为均值0，收敛更快），但仍然存在梯度消失问题，尤其在深层网络。

D ReLU

在正区梯度恒为 1，不会因激活函数本身导致梯度衰减（无饱和区），能有效缓解梯度消失。但可能有神经元死亡问题（负半区梯度为 0）。

9. 混合精度训练中引入**"损失缩放"**的主要原因是（）。

在混合精度训练中，使用 FP16 表示时，梯度的值可能非常小（小于 FP16 能表示的最小正数 ~ 6e-8），导致在反向传播时梯度变为 0 ，这种现象称为梯度下溢。

损失缩放（Loss Scaling） 的做法是在计算损失函数后，将其乘以一个缩放因子 （如 1024），这样在反向传播时梯度也会等比例放大，使其进入 FP16 的可表示范围，避免下溢。在权重更新前，再将梯度按同样比例缩小回来。

因此，主要原因是 B 防止低精度下梯度下溢为零。

10. 内存计算：在一个由 8 张 A100-80GB 组成的集群上，上线双塔检索：文档塔输出 d 维 float32 向量，文档库 2 亿条，所有向量需常驻显存，且不能用 CPU/磁盘缓存；单卡可用显存约 75GB。问在不压缩、不量化、不断层拆分的前提下，d 的上限？

75G * 8 = 600 * 1e9 B > d*4B(float32) *2e8

11.关于 Causal Mask说法正确的是？

A 是一个上三角为 −∞ 的矩阵

B 防止训练时看到未来信息

C 仅用于文本生成任务 （错，音频、图像等也可，不只是文本）

D 用于增强自注意力的局部性（错，强调不看后面，前面都可以看，而不是小局部）