目录
[Registration System](#Registration System)
[Obsession with Robots](#Obsession with Robots)
引言:
今天是算法沉淀的第五天,我们接着来打CF的题,因为今天的题没有1500,所以我就开了一道1300的题后又开了一道1400的题,如图

那么,我们今天就来讲讲这俩道题,话不多说,我们就进入今天的算法讲解--------------------->

Registration System
按照惯例,先看题目
题意分析
这是题目链接Problem - 4C - Codeforces
不想跳转的可看下图

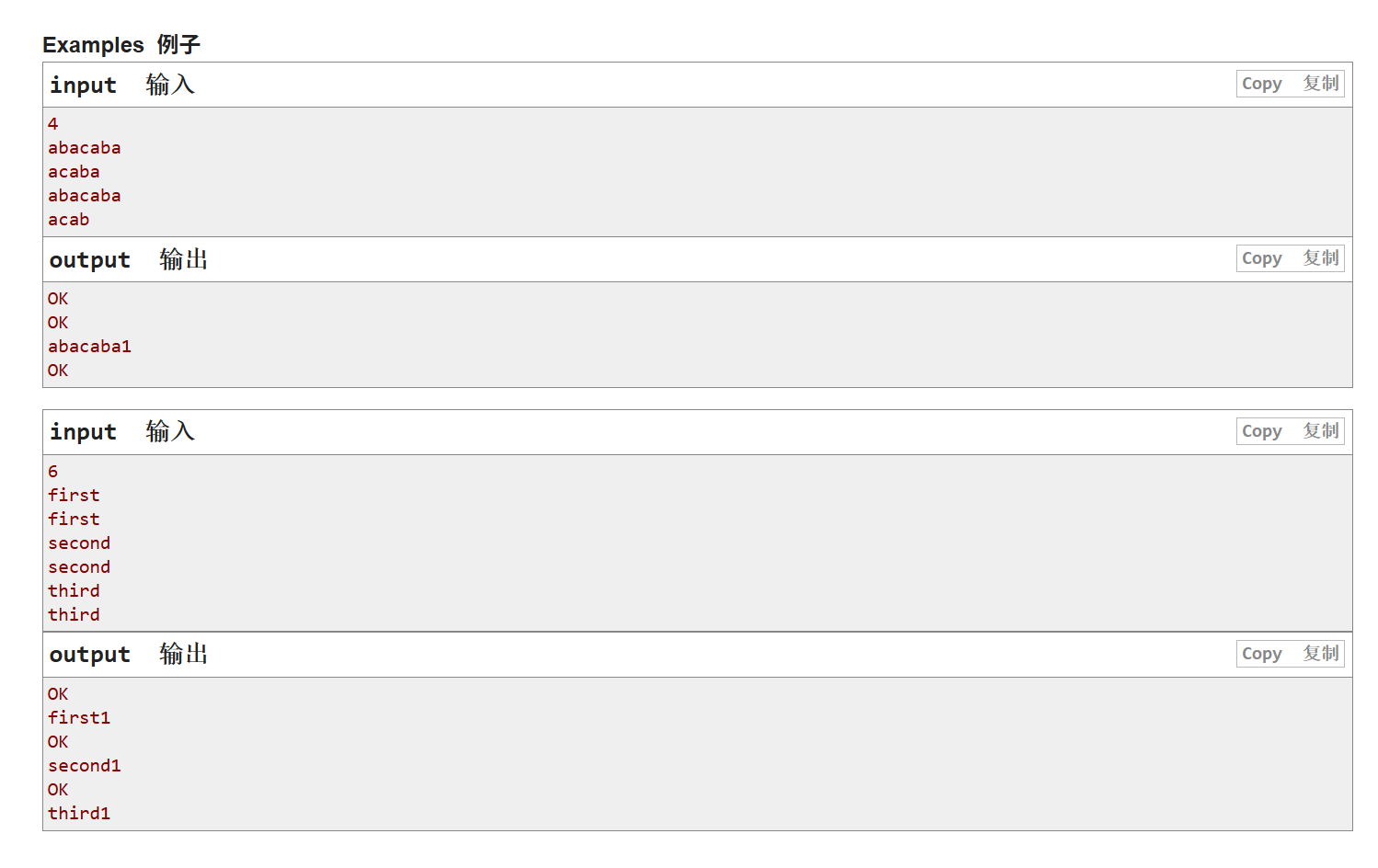
这题的意思很简单,就是让你输入字符串,然后每次输入字符串判断这个字符串之前有没有输入过
如果没有输入过,就输出OK
如果输入过了,就输出这个字符串然后后面再接上一个数字
那这个数字接多少呢,就相当于前面如果这个名字出现了n次,就接个n-1的数字,因为名字第一次出现时候不用接数字
那么,这题的题目意思就分析完了,是不是很简单,这功能也挺像有些古早游戏取名重复时候在原名字后面接数字提示的那个功能
接下来,我们就进入逻辑梳理环节
逻辑梳理
这题的逻辑其实挺简单的,因为数据范围并不大,所以直接暴力就好了,我们先开个结构体,结构体里面存名字和这个名字出现的次数,然后再创一个字符串来输入
然后每次输入,先进行循环,来找当前结构体中有没有出现过这个名字,如果没有出现过,就将结构体下标往后移一位,然后存进去这个名字,然后将出现的次数设置成0,并且输出OK,然后结束这一次的判断
如果这个名字出现过,就将那个名字所在的结构体下标中的次数加一次,然后先输出这个名字,再输出这个名字对应的次数就可以了,然后再结束这一次的判断就可以了
那么,这题的逻辑梳理就梳理完啦,接下来,就进入代码实现环节
代码实现
这题的逻辑还是挺简单的,那么就直接放AC码啦
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
int n;
int wei = 0;
struct people
{
string ren;
int ci;
}a[100010];
void solve()
{
string A;
cin >> A;
for (int i = 0; i < wei; i++)
{
if (a[i].ren.size() == A.size())
{
int xi = 1;
string B = a[i].ren;
for (int j = 0; j < A.size(); j++)
{
if (A[j] != B[j])
{
xi = 0;
break;
}
}
if (xi)
{
a[i].ci++;
cout << A << a[i].ci << endl;
return;
}
}
}
a[wei].ren = A;
a[wei++].ci = 0;
cout << "OK" << endl;
}
int main()
{
cin >> n;
while (n--)
{
solve();
}
return 0;
}那么,这题就讲完啦
Obsession with Robots
题意分析
这是题目链接 Problem - 8B - Codeforces
不想跳转的可看下图

这题的意思也很简单,就是给你一串机器人的指令,代表机器人的移动情况
然后地图的障碍物和空地可以随便放置,只要存在一种放置方法可以让这个机器人从起点到终点走的路是最短路就可以了
如果存在这种地图,那就输出OK
如果不存在这种地图,那就输出BUG
那么这题的题意就分析完啦,接下来我们就进入逻辑梳理环节
逻辑梳理
这题因为地图可以自己设置嘛,只要有一个地图能满足条件就可以了,那我们就把这地图当成全是障碍物,然后空地只留机器人走的那几步的路程
那么,这样的地图分布是不是就是最好的地图绘制啦,那么我们只需要判断在这个地图的情况下是不是最短路了
那么,我们就来想想,什么情况下不是最短路,把不是最短路的情况全都排除掉后就肯定是最短路的情况了
第一种:成环
如果走着走着又走回之前走过的点了,那就肯定不满足最短路的情况了
这种只需要一个二维数组来存走过的点就可以了,每次走之后将到的点标记为访问过,然后如果之后走到访问过的点的时候就直接输出BUG结束程序就可以了
第二种:十字格有2个以上位置走过
这种情况是我在WA一次之后才意识到的,如图

这三步虽然都没有走到访问过的点,但是看这个图很明显,如果十字格上有2个位置被走过了,那么这个路线就肯定不是最短路了,因为如果有多个点访问过的话,就说明一个点是上一步走的点,但是还有其他点多出来了,那就可以从那个点直接走到这个点,这就省了很多步
所以这俩种情况都考虑到后 ,这题就自然迎刃而解了,那么接下来就进入代码实现的环节
代码实现
这里就直接放AC码啦
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <queue>
using namespace std;
string a;
bool vis[220][220];
void solve()
{
vis[110][110] = 1;
int x = 110;
int y = 110;
cin >> a;
for (int i = 0; i < a.size(); i++)
{
if (a[i] == 'L')
{
y--;
if (!vis[x][y])
{
vis[x][y] = 1;
int t = 0;
if (vis[x][y + 1])
t++;
if (vis[x + 1][y])
t++;
if (vis[x - 1][y])
t++;
if (vis[x][y - 1])
t++;
if (t >= 2)
{
cout << "BUG" << endl;
return;
}
}
else
{
cout << "BUG" << endl;
return;
}
}
if (a[i] == 'R')
{
y++;
if (!vis[x][y])
{
vis[x][y] = 1;
int t = 0;
if (vis[x][y + 1])
t++;
if (vis[x + 1][y])
t++;
if (vis[x - 1][y])
t++;
if (vis[x][y - 1])
t++;
if (t >= 2)
{
cout << "BUG" << endl;
return;
}
}
else
{
cout << "BUG" << endl;
return;
}
}
if (a[i] == 'U')
{
x--;
if (!vis[x][y])
{
vis[x][y] = 1;
int t = 0;
if (vis[x][y + 1])
t++;
if (vis[x + 1][y])
t++;
if (vis[x - 1][y])
t++;
if (vis[x][y - 1])
t++;
if (t >= 2)
{
cout << "BUG" << endl;
return;
}
}
else
{
cout << "BUG" << endl;
return;
}
}
if (a[i] == 'D')
{
x++;
if (!vis[x][y])
{
vis[x][y] = 1;
int t = 0;
if (vis[x][y + 1])
t++;
if (vis[x + 1][y])
t++;
if (vis[x - 1][y])
t++;
if (vis[x][y - 1])
t++;
if (t >= 2)
{
cout << "BUG" << endl;
return;
}
}
else
{
cout << "BUG" << endl;
return;
}
}
}
cout << "OK" << endl;
return;
}
int main()
{
solve();
return 0;
}那么,这题也讲完啦
结语:
今日算法讲解到此结束啦,希望对你们有所帮助,谢谢观看,如果觉得不错可以分享给朋友哟。有什么看不懂的可以评论问哦,
