文章目录
-
- 红黑树
-
- 介绍
- 五大规则
- 保持平衡
- 插入操作(简述)
- 对比AVL树
- 一、红黑树是什么?
- 二、红黑树的五大规则
- 三、⭐红黑树如何保持平衡?(核心操作)
- [四、红黑树 vs AVL树](#四、红黑树 vs AVL树)
- 五、Java实现
红黑树
介绍
红黑树是另一种重要的平衡二叉树,通过颜色标记和旋转维护平衡。
由于其自平衡的特性,保证了最坏情形下在 O(logn) 时间复杂度内完成查找、增加、删除等操作,性能表现稳定。
五大规则
红黑树之所以能保持平衡,是因为它遵循以下五个基本规则。这些规则是定义红黑树的核心:
- 节点是红色或黑色:每个节点都有一个颜色属性,非红即黑。
- 根节点是黑色:树的顶端根节点必须是黑色的。
- 所有叶子节点都是黑色:这里的叶子节点指的是空指针(NIL或NULL节点),被视为黑色的哨兵节点。
- 红色节点的子节点必须是黑色 :这意味着不会有两个连续的红色节点出现。这是保证平衡的关键规则之一。
- 从任意节点到其每个叶子节点的所有路径都包含相同数目的黑色节点:这个数量被称为该节点的"黑高"。这条规则确保了没有一条路径会比其他路径长出两倍以上,是平衡性的最强保证。
规则4和规则5是精髓:
- 规则4限制了红色节点的连续出现,控制了树的"横向"蔓延。
- 规则5确保了从根到叶子的所有路径中,黑色节点的数量是严格相等的,这就像是为树的深度设定了一个基准。
保持平衡
当插入或删除节点可能破坏上述规则时,红黑树需要通过两种基本操作来修复平衡:
- 变色:改变节点的颜色(红变黑,或黑变红)。这是最直接、代价最小的调整方式。
- 旋转:通过改变树的结构来重新平衡。
- 左旋:以某个节点为支点,让其右子节点成为新的父节点。
- 右旋:以某个节点为支点,让其左子节点成为新的父节点。
旋转操作是局部操作,时间复杂度是O(1),不会影响整棵树的大局。
插入操作(简述)
新插入的节点通常被标记为红色(因为标记为黑色会立刻违反规则5,影响太大)。插入后,检查是否破坏了规则:
-
情况1:如果新节点的父节点是黑色,没有违反任何规则,无需调整。
-
情况2:如果父节点是红色(违反了规则4),则需要根据其"叔叔节点"(父节点的兄弟节点)的颜色进行进一步处理:
-
情况2.1 :叔叔节点是红色。通过将父节点和叔叔节点变黑,祖父节点变红来解决。然后可能将问题向上传递到祖父节点。
-
情况2.2 :叔叔节点是黑色 (或NIL)。这种情况需要通过旋转 和变色的组合来解决。可能是左左、左右、右右、右左等不同情况,通过相应的旋转(单旋或双旋)来调整结构。
对比AVL树
好的,我们用一个系统、易懂的方式来介绍一下红黑树。
一、红黑树是什么?
简单来说,红黑树是一种自平衡的二叉查找树。
- 二叉查找树:首先,它具备二叉查找树的所有特性:对于任意节点,其左子树所有节点的值都小于它,右子树所有节点的值都大于它。这使得查找、插入、删除等操作非常高效(平均时间复杂度O(log n))。
- 自平衡:这是红黑树的核心。普通的二叉查找树在插入或删除节点时,如果数据是顺序插入的(如1,2,3,4,5),树会退化成一条"链",查找效率会降至O(n)。红黑树通过一套严格的规则和相应的调整操作(变色、旋转),确保树始终保持"大致平衡",从而保证在最坏情况下的操作效率也是O(log n)。
你可以把它想象成一个能自动整理书籍的超智能书架。无论你按什么顺序往书架上放书(比如按照书名拼音顺序、出版日期乱序等),这个书架都会通过内部机制自动调整,让书与书之间的间隔保持相对均匀,你总能快速地找到任何一本书。
二、红黑树的五大规则
红黑树之所以能保持平衡,是因为它遵循以下五个基本规则。这些规则是定义红黑树的核心:
- 节点是红色或黑色:每个节点都有一个颜色属性,非红即黑。
- 根节点是黑色:树的顶端根节点必须是黑色的。
- 所有叶子节点都是黑色:这里的叶子节点指的是空指针(NIL或NULL节点),被视为黑色的哨兵节点。
- 红色节点的子节点必须是黑色 :这意味着不会有两个连续的红色节点出现。这是保证平衡的关键规则之一。
- 从任意节点到其每个叶子节点的所有路径都包含相同数目的黑色节点:这个数量被称为该节点的"黑高"。这条规则确保了没有一条路径会比其他路径长出两倍以上,是平衡性的最强保证。
规则4和规则5是精髓:
- 规则4限制了红色节点的连续出现,控制了树的"横向"蔓延。
- 规则5确保了从根到叶子的所有路径中,黑色节点的数量是严格相等的,这就像是为树的深度设定了一个基准。
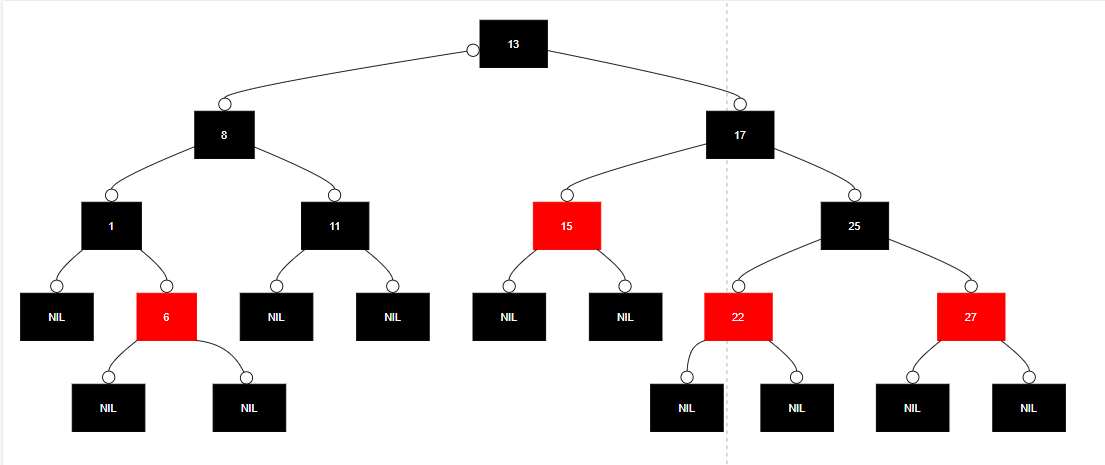
三、⭐红黑树如何保持平衡?(核心操作)
当插入或删除节点可能破坏上述规则时,红黑树需要通过两种基本操作来修复平衡:
- 变色:改变节点的颜色(红变黑,或黑变红)。这是最直接、代价最小的调整方式。
- 左倾染色:
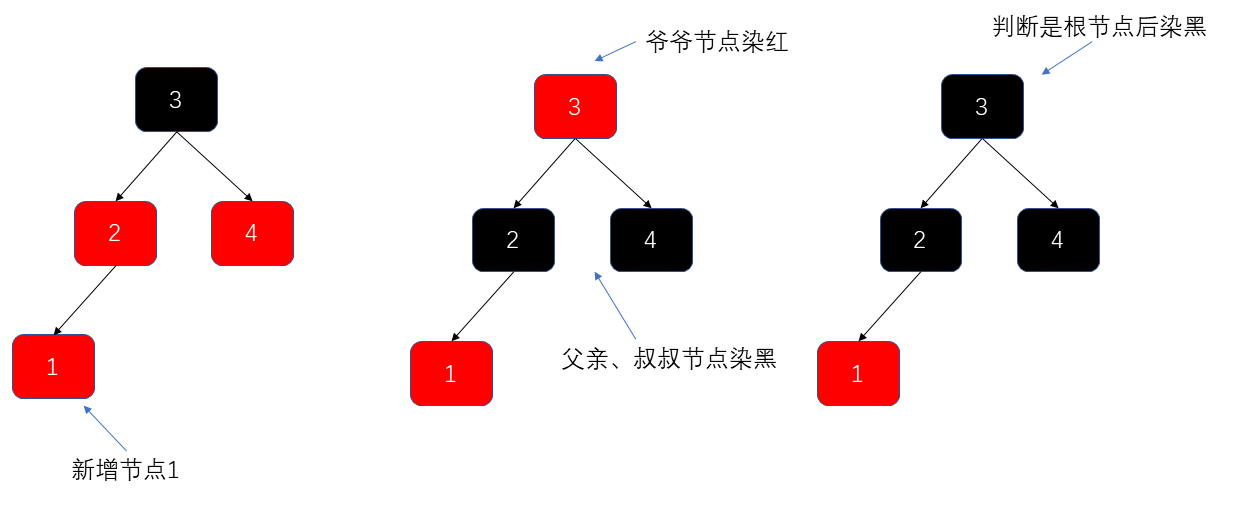
- 右倾染色:
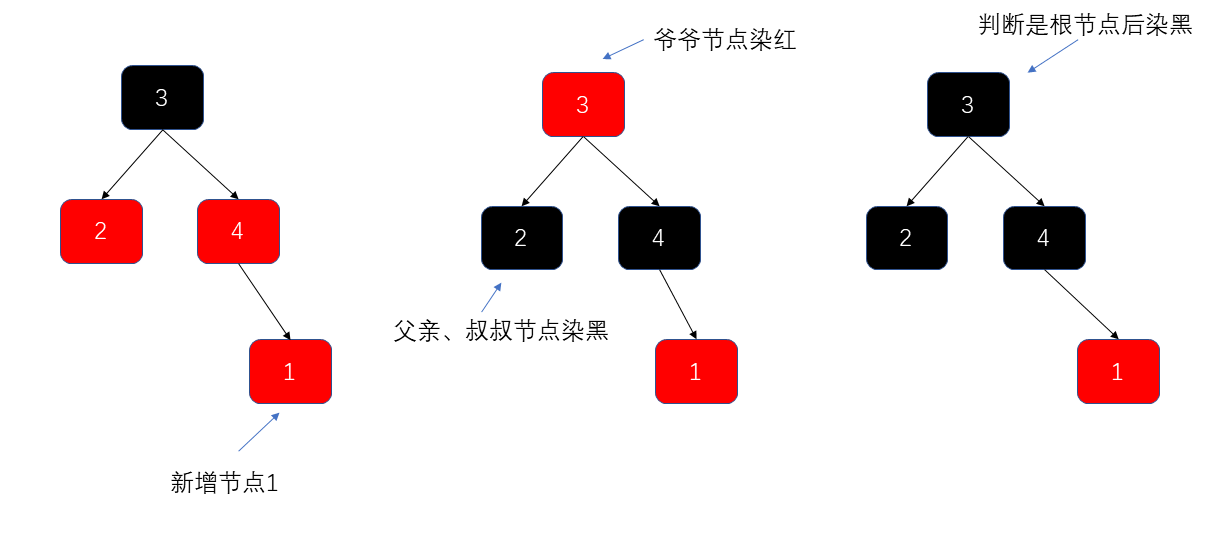
- 旋转:通过改变树的结构来重新平衡。
- 左旋:以某个节点为支点,让其右子节点成为新的父节点。
- 右旋:以某个节点为支点,让其左子节点成为新的父节点。
旋转操作是局部操作,时间复杂度是O(1),不会影响整棵树的大局。
- 左旋
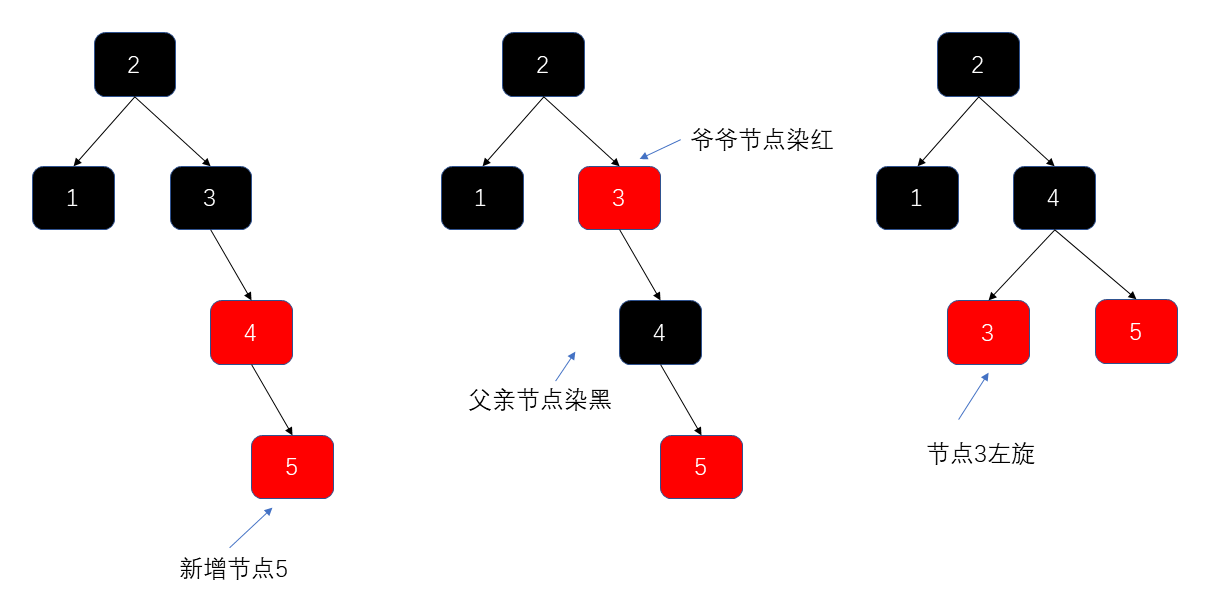
- 右旋+左旋
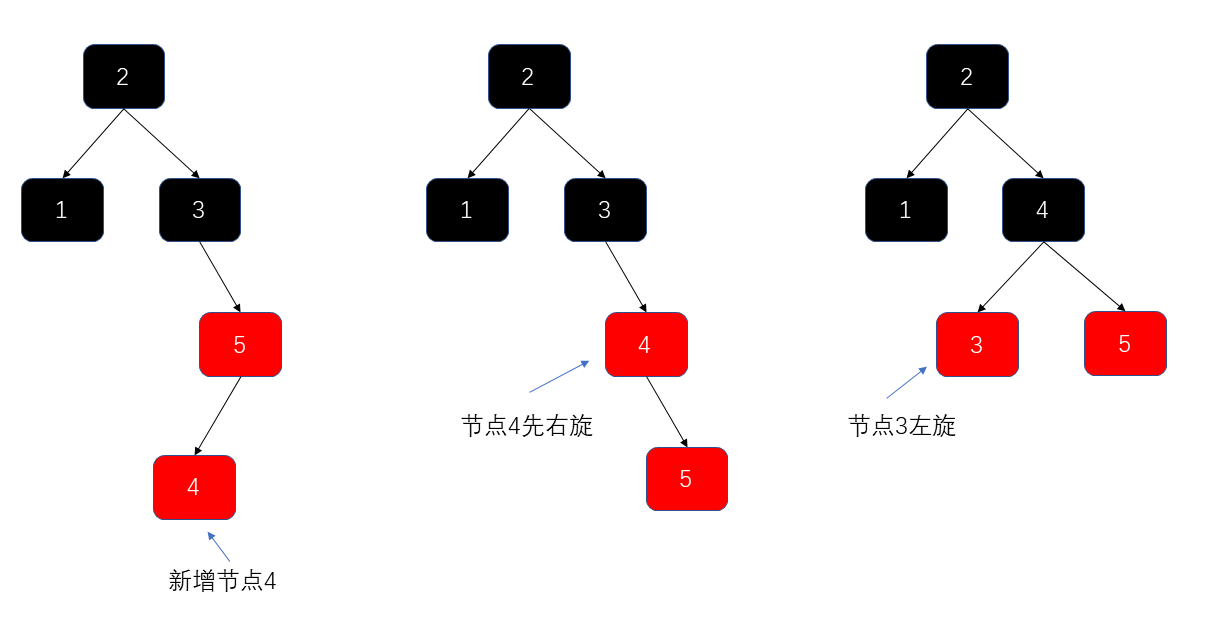
- 右旋
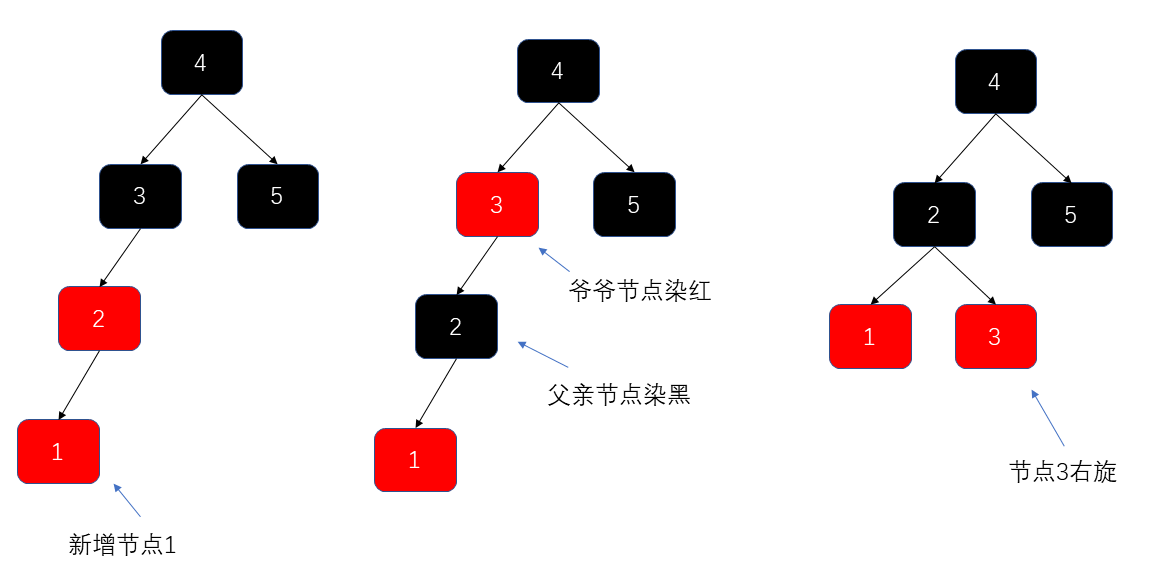
- 左旋+右旋
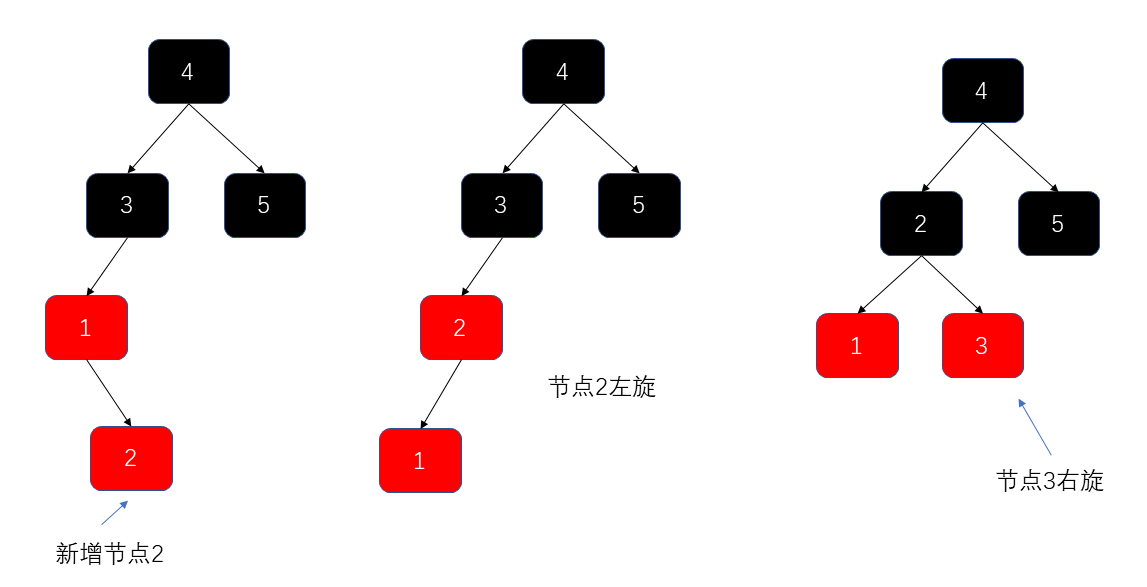
⭐插入操作的平衡调整(简述)
新插入的节点通常被标记为红色(因为标记为黑色会立刻违反规则5,影响太大)。插入后,检查是否破坏了规则:
-
情况1:如果新节点的父节点是黑色,没有违反任何规则,无需调整。
-
情况2:如果父节点是红色(违反了规则4),则需要根据其"叔叔节点"(父节点的兄弟节点)的颜色进行进一步处理:
-
情况2.1 :叔叔节点是红色。通过将父节点和叔叔节点变黑,祖父节点变红来解决。然后可能将问题向上传递到祖父节点。
-
情况2.2 :叔叔节点是黑色 (或NIL)。这种情况需要通过旋转 和变色的组合来解决。可能是左左、左右、右右、右左等不同情况,通过相应的旋转(单旋或双旋)来调整结构。
通过这一系列的变色和旋转,最终让树重新满足所有红黑树规则。
四、红黑树 vs AVL树
AVL树是另一种著名的自平衡二叉查找树,它通过高度差(平衡因子) 来维持更严格的平衡。
| 特性 | 红黑树 | AVL树 |
|---|---|---|
| 平衡标准 | 规则4和规则5(较为宽松) | 每个节点的左右子树高度差不超过1(非常严格) |
| 平衡度 | 大致平衡,不是完全平衡 | 高度平衡,是更严格的平衡 |
| 查询效率 | 查询效率稍低,但稳定在O(log n) | 查询效率最高,因为树更平衡 |
| 插入/删除效率 | 更高。因为平衡要求宽松,需要的旋转操作更少 | 较低。插入/删除后可能需要更多的旋转来维持严格平衡 |
| 适用场景 | 频繁增删的场景,如关联数组(Map、Set) | 频繁查询,少增删的场景,如数据库索引 |
总结选择:
- 如果你的应用需要大量的查找操作,而插入和删除不频繁,AVL树是更好的选择。
- 在现实中,需要大量插入、删除和查找操作的场景更为常见,因此红黑树的应用更加广泛。
五、Java实现
基本结构
java
@Data
public class RBNode<T extends Comparable<T>> {
private T data;
private Color color;
RBNode<T> left, right, parent;
public RBNode(T data) {
this.data = data;
this.color = Color.RED; // 新节点默认为红色
this.left = this.right = this.parent = null;
}
}
public class RedBlackTree <T extends Comparable<T>>{
private RBNode<T> root;
private final RBNode<T> NIL; // 哨兵节点(叶子节点)
public RedBlackTree() {
NIL = new RBNode<>(null);
NIL.setColor(Color.BLACK);
root = NIL;
}
}左右旋
java
// 左旋操作
private void leftRotate(RBNode<T> x) {
RBNode<T> y = x.right;
x.right = y.left;
if (y.left != NIL) {
y.left.parent = x;
}
y.parent = x.parent;
if (x.parent == NIL) {
root = y;
} else if (x == x.parent.left) {
x.parent.left = y;
} else {
x.parent.right = y;
}
y.left = x;
x.parent = y;
}
// 右旋操作
private void rightRotate(RBNode<T> y) {
RBNode<T> x = y.left;
y.left = x.right;
if (x.right != NIL) {
x.right.parent = y;
}
x.parent = y.parent;
if (y.parent == NIL) {
root = x;
} else if (y == y.parent.left) {
y.parent.left = x;
} else {
y.parent.right = x;
}
x.right = y;
y.parent = x;
}插入方法
java
// 插入方法
public void insert(T data) {
RBNode<T> node = new RBNode<>(data);
node.left = NIL;
node.right = NIL;
node.parent = NIL;
RBNode<T> current = root;
RBNode<T> parent = NIL;
// 二叉搜索树插入
while (current != NIL) {
parent = current;
if (node.getData().compareTo(current.getData()) < 0) {
current = current.left;
} else {
current = current.right;
}
}
node.parent = parent;
if (parent == NIL) {
root = node;
} else if (node.getData().compareTo(parent.getData()) < 0) {
parent.left = node;
} else {
parent.right = node;
}
fixInsert(node); // 修复红黑树性质
}
// 修复插入后的红黑树性质
private void fixInsert(RBNode<T> node) {
while (node.parent.getColor() == Color.RED) {
if (node.parent == node.parent.parent.left) {
RBNode<T> uncle = node.parent.parent.right;
// Case 1: 叔叔节点是红色
if (uncle.getColor() == Color.RED) {
node.parent.setColor(Color.BLACK);
uncle.setColor(Color.BLACK) ;
node.parent.parent.setColor(Color.RED);
node = node.parent.parent;
} else {
// Case 2: 节点是父节点的右孩子
if (node == node.parent.right) {
node = node.parent;
leftRotate(node);
}
// Case 3: 节点是父节点的左孩子
node.parent.setColor(Color.BLACK);
node.parent.parent.setColor(Color.RED);
rightRotate(node.parent.parent);
}
} else {
// 对称情况(父节点是右孩子)
RBNode<T> uncle = node.parent.parent.left;
if (uncle.getColor() == Color.RED) {
node.parent.setColor(Color.BLACK);
uncle.setColor(Color.BLACK);
node.parent.parent.setColor(Color.RED);
node = node.parent.parent;
} else {
if (node == node.parent.left) {
node = node.parent;
rightRotate(node);
}
node.parent.setColor(Color.BLACK);
node.parent.parent.setColor(Color.RED);
leftRotate(node.parent.parent);
}
}
}
root.setColor(Color.BLACK); // 确保根节点为黑色
}