参考链接:
【B树(B-树) - 来由, 定义, 插入, 构建】https://www.bilibili.com/video/BV1tJ4m1w7yR?vd_source=c744ec928a14e81c8bf974e8d2d7e80f
查找并不是一次性加载到内存查找,而是分多次硬盘访问:
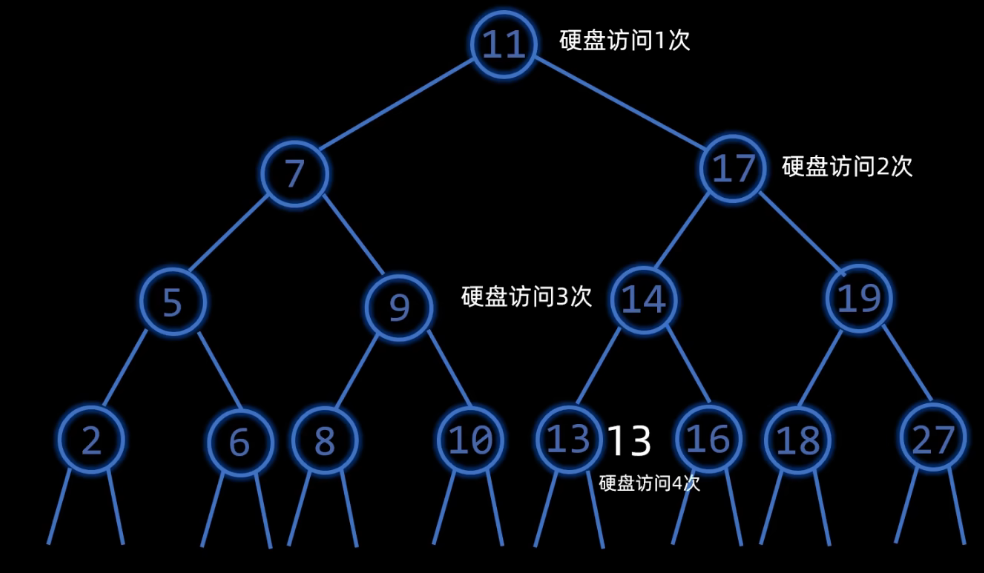
可以看出硬盘访问次数和树高正相关,而硬盘的访问速度非常慢,所以需要减少访问次数,也就是要降低树的高度。
B树就是一个多叉平衡搜索树,这样每个节点就可以保存更多的数据了,进而树的高度被压缩了。(硬盘访问次数减少了,但是节点里面的元素个数变多了,是否会导致硬盘访问节点的时候增加耗时呢? -- 硬盘读取物理地址连续的多个字节和读取单个字节耗时几乎没有区别)
访问节点是在硬盘中进行的,节点内的数据操作是在内存中进行的。
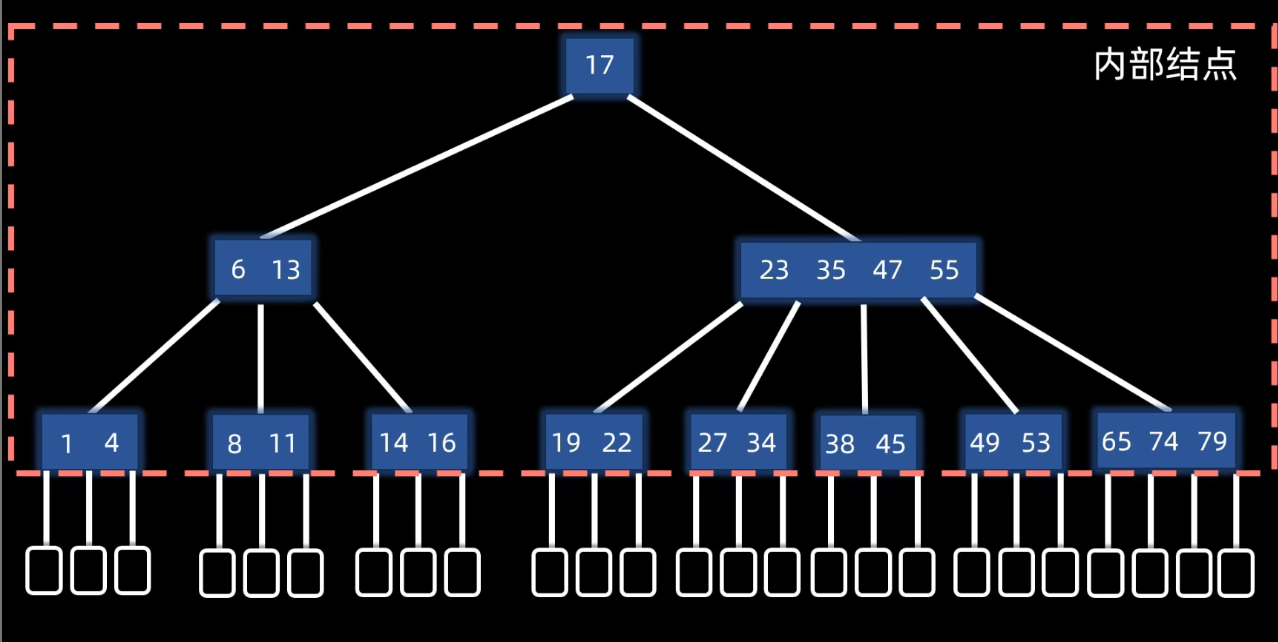
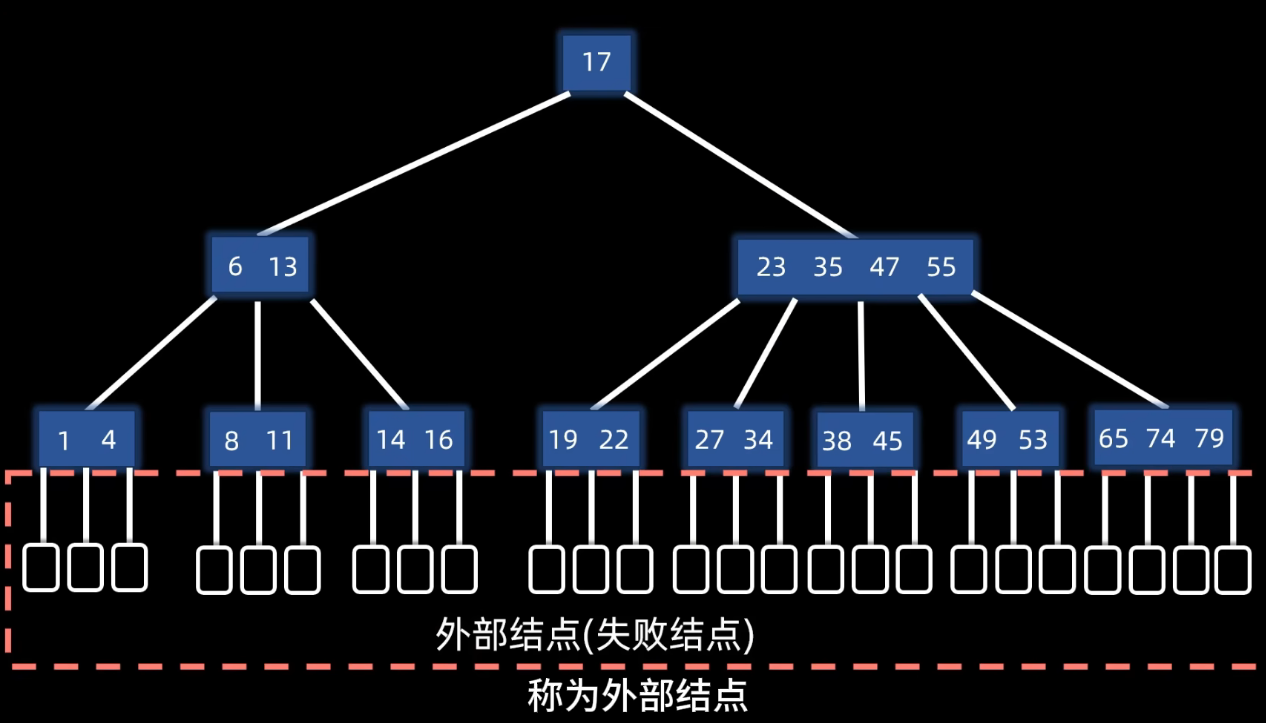
B树满足的三个特性:
- 平衡:所有的叶节点都在同一层
- 有序:节点内有序,同时任意元素的左子树都小于它,右子树都大于它
- 多路:对于m阶B树的节点:
- 最多:m个分支,m-1个元素
- 最少:
- 根节点:2个分支,1个元素
- 其他节点:ceil(m / 2)个分支,ceil(m / 2) - 1个元素。
查找操作:
对于同一个节点多个数据可以采取:二分查找或者顺序查找;如果目标节点处于同一层节点任意两个节点之间(或者在最左/最右)则通过子树向下查找。
如果节点数据相同,则数据存在,查找失败。
如果走到失败节点,则数据不存在,查找结束。
插入操作:
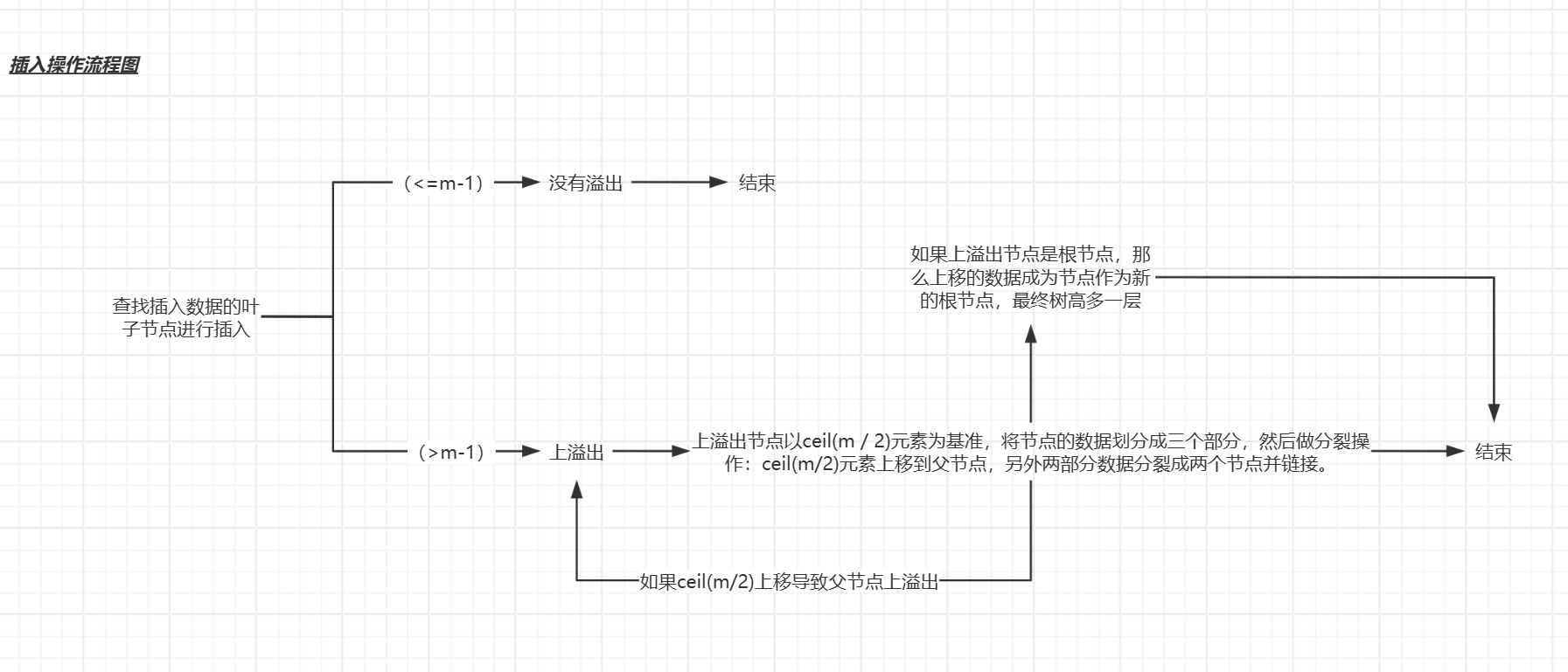
通过查找,找到插入数据的叶子节点(最后一层有效数据节点,不是失败节点),按照在节点内的顺序位置插入。
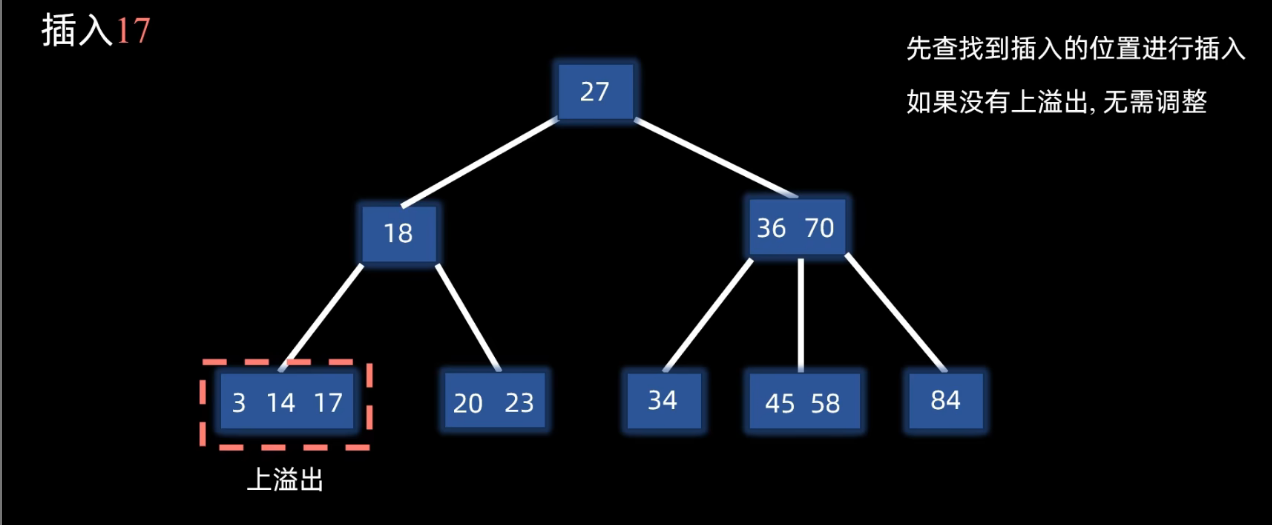
插入后的情况--没有溢出:直接插入,无需调整。
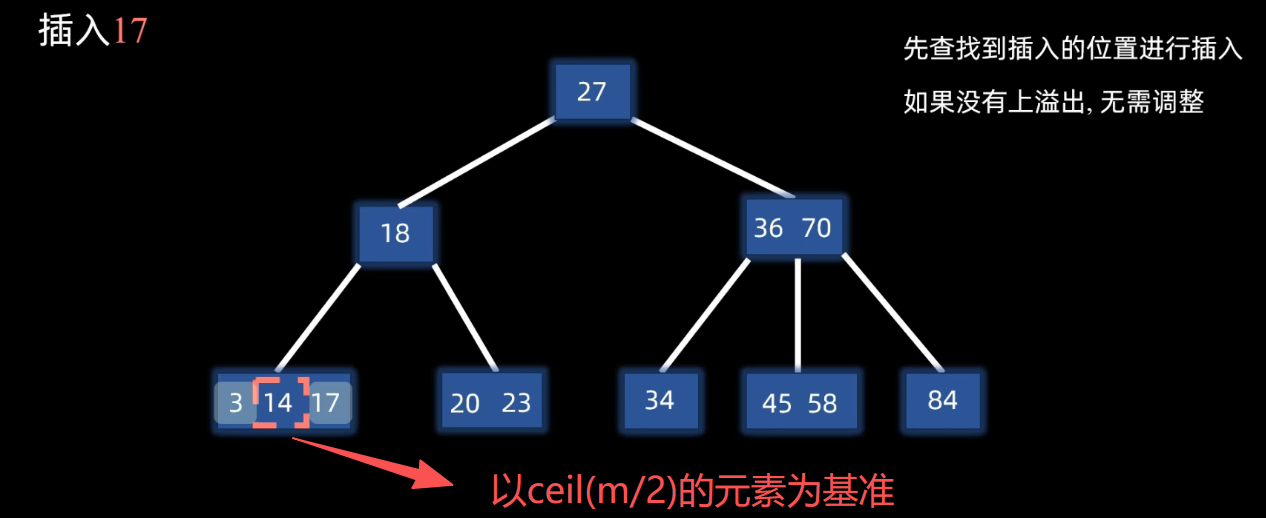
插入后的情况--上溢出:插入节点之后会超过节点数据上限m-1;需要调整。
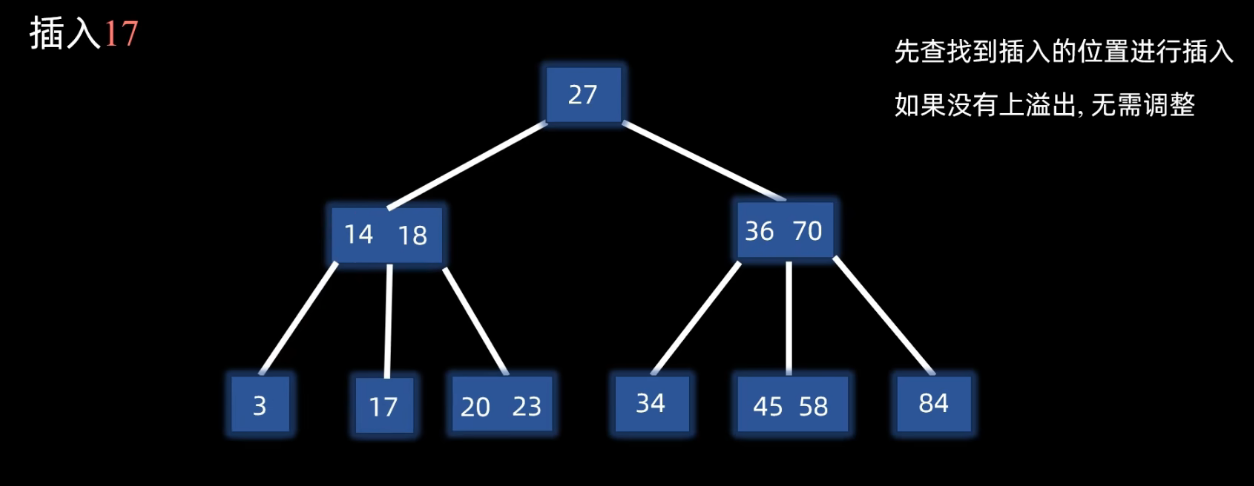
上溢出调整:上溢出节点以ceil(m / 2)元素为基准,将节点的数据划分成三个部分,然后做分裂操作:ceil(m/2)元素上移到父节点,另外两部分数据分裂成两个节点并链接。
如果插入到父节点之后:父节点也溢出,按同样的上溢出操作继续调整,直到不发生溢出。
如果根节点也上溢出:继续进行上溢出操作,上移动的数据成为节点作为新的根节点,最终树高多了一层。
删除操作:
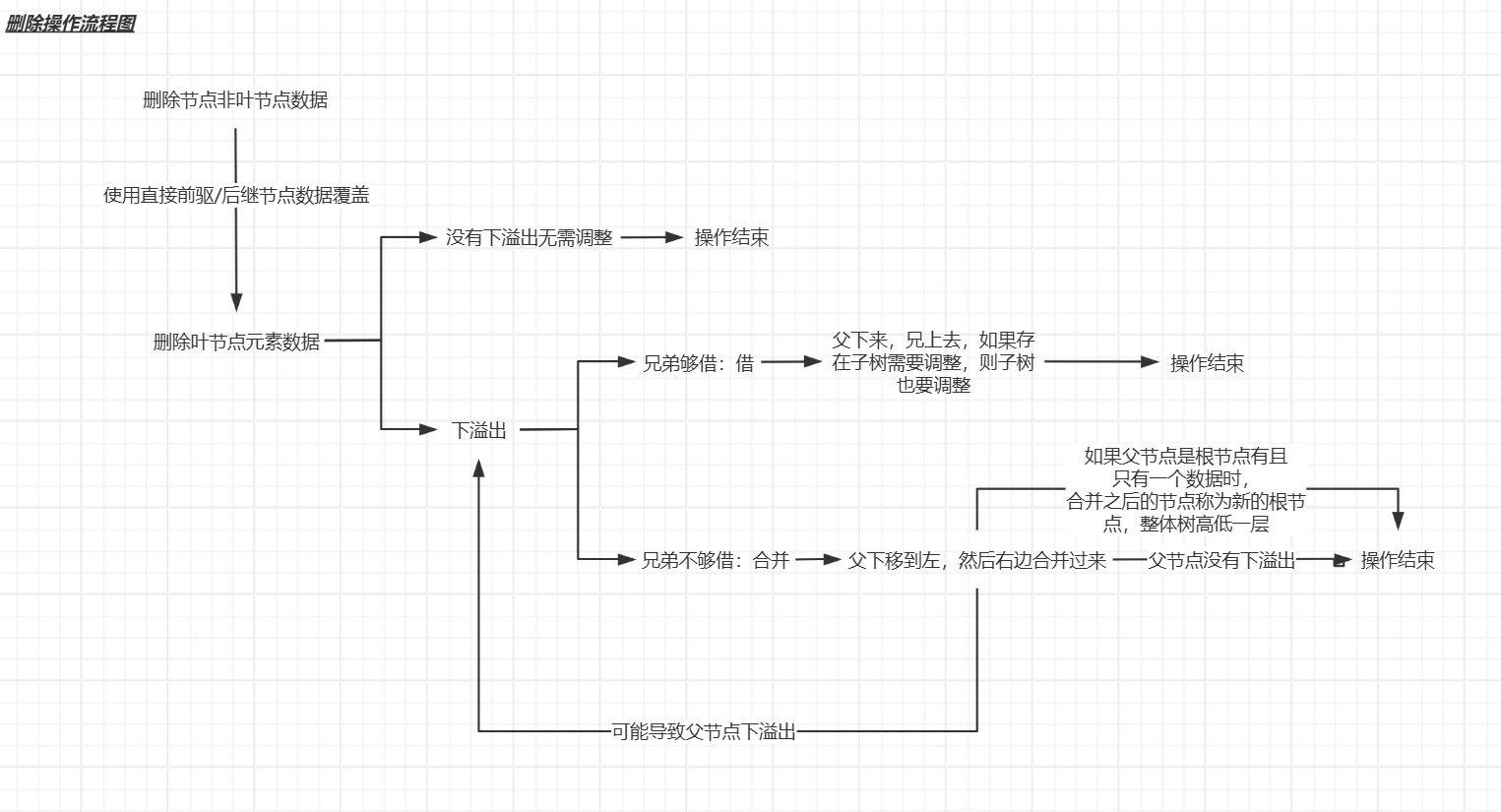
删除非叶子节点:使用直接前驱或者直接后继去替换它,转化为删除叶子节点。
删除叶子节点:直接删除,如果出现下溢出(删除后节点元素数量少于ceil(m/2) - 1)则需要进行下溢出调整操作;否则无需调整。
下溢出调整操作:向左/右兄弟借
- 兄弟够借:借;将删除节点数据的父节点数据拉下来与删除节点数据放在同一个节点,然后将兄弟节点数据上移到上一层(父下来,兄上去),如果存在子树需要调整,则子树也要调整;调整结束。
- 兄弟不够借:与左/右兄弟合并;删除节点数据的父节点数据下移到左节点,再将右边的节点数据右并过来左节点,最后移除空的父元素和空子树即可(父下移到左,然后右并过来 )(如果父节点是根节点有且只有一个数据时,合并之后的节点称为新的根节点,整体树高低一层)如果父节点也出现下溢出同样执行下溢出调整操作。
模板:
cpp
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
namespace nsBTree
{
//M叉树:一个节点最多有M个孩子,M-1个数据域
//为了实现简单,数据域与孩子域多增加一个,有效数据由_size决定
template<class K, int M = 3>
struct BTreeNode
{
K _keys[M]; //数据域
BTreeNode<K, M>* _pSub[M + 1]; //孩子节点
BTreeNode<K, M>* _pParent; //父节点
int _size; //节点中有效元素的个数
BTreeNode()
:_pParent(nullptr), _size(0)
{
for (int i = 0; i <= M; ++i)
_pSub[i] = nullptr;
}
};
template<class K, int M = 3>
class BTree
{
typedef BTreeNode<K, M>* PNode;
typedef BTreeNode<K, M> Node;
private:
void _Erase(PNode pCur, const int delKeyIdx)
{
//释放节点
if (pCur->_pSub[delKeyIdx + 1] != nullptr)
{
delete pCur->_pSub[delKeyIdx + 1];
pCur->_pSub[delKeyIdx + 1] = nullptr;
}
//覆盖,i - 1被覆盖,i去覆盖
for (int i = delKeyIdx + 1; i < pCur->_size; i++)
{
pCur->_keys[i - 1] = pCur->_keys[i];
pCur->_pSub[i] = pCur->_pSub[i + 1]; //if == nullptr -> nullptr = nullptr or if == !nullptr -> !nullptr = !nullptr
}
--pCur->_size;
}
void _InsertKey(PNode pCur, const K& key, PNode pSub)
{
//按照插入排序思想插入key
int end = pCur->_size - 1;
//end位置用于比较,end+1位置用于存储
while (end >= 0)
{
if (key < pCur->_keys[end])
{
pCur->_keys[end + 1] = pCur->_keys[end];
pCur->_pSub[end + 2] = pCur->_pSub[end + 1];
end--;
}
else
break;
}
pCur->_keys[end + 1] = key;
pCur->_pSub[end + 2] = pSub;
if (pSub)
pSub->_pParent = pCur;
pCur->_size++;
}
//void _InOrder(const PNode pRoot)
//{
// if (pRoot == nullptr)
// return;
// for (int i = 0; i < pRoot->_size; ++i)
// {
// _InOrder(pRoot->_pSub[i]);
// _testV.push_back(pRoot->_keys[i]);
// //cout << pRoot->_keys[i] << endl;
// }
// _InOrder(pRoot->_pSub[pRoot->_size]);
//}
public:
BTree()
:_pRoot(nullptr), _floor(ceil((double)M / 2) - 1) //注意不要写出:ceil(M / 2) - 1,因为M/2之后的临时变量也是整型,会先阶段小数点后面的数,再传给ceil的double形参,这样就会导致计算结果不会向上取整。
{}
pair<PNode, int> Find(const K& key)
{
PNode pCur = _pRoot;
PNode pParent = nullptr;
int i = 0;
while (pCur)
{
i = 0;
while (i < pCur->_size)
{
if (key == pCur->_keys[i])
return pair<PNode, int>(pCur, i);
else if (key < pCur->_keys[i])
break;
else
++i;
}
pParent = pCur;
pCur = pCur->_pSub[i];
}
return pair<PNode, int>(pParent, -1);
}
bool Insert(const K& key)
{
//空树直接插入
if (_pRoot == nullptr)
{
_pRoot = new Node();
_pRoot->_keys[0] = key;
_pRoot->_size = 1;
return true;
}
//非空树
pair<PNode, int> ret = Find(key);
//如果已经存在,插入失败
if (ret.second != -1)
return false;
K k = key;
PNode temp = nullptr;
PNode pCur = ret.first;
while (true)
{
//key插入
_InsertKey(pCur, k, temp);
//检查是否存在上溢出
if (pCur->_size < M)
return true;
//上溢出了
temp = new Node;
int mid = (M >> 1); //基准值=ceil(M / 2)
//基准值右边迁移到新节点
for (int i = mid + 1; i < pCur->_size; ++i)
{
temp->_keys[temp->_size] = pCur->_keys[i];
temp->_pSub[temp->_size++] = pCur->_pSub[i];
if (pCur->_pSub[i])
pCur->_pSub[i]->_pParent = temp;
}
//孩子比数据域多一个
temp->_pSub[temp->_size] = pCur->_pSub[pCur->_size];
if (pCur->_pSub[pCur->_size])
pCur->_pSub[pCur->_size]->_pParent = temp;
//更新左孩子有效数据个数即可
pCur->_size -= (temp->_size + 1);
//分裂操作
//如果分裂的是根节点
if (pCur == _pRoot)
{
_pRoot = new Node;
_pRoot->_keys[0] = pCur->_keys[mid];
_pRoot->_pSub[0] = pCur;
_pRoot->_pSub[1] = temp;
_pRoot->_size = 1;
pCur->_pParent = temp->_pParent = _pRoot;
return true; //直接结束
}
else
{
//如果分裂节点不是根节点,则temp作为上一层新插入的节点继续执行插入操作
k = pCur->_keys[mid];
pCur = pCur->_pParent;
}
}
return true;
}
bool Erase(const K& key)
{
//查找到目标删除节点数据位置
pair<PNode, int> ret = Find(key);
//不存在
if (ret.second == -1)
return false;
//查找到直接前驱节点/后继节点,key替换,目标删除节点变成直接后继(叶节点
PNode del = ret.first;
int delIdx = ret.second;
//判断是否在叶子节点--不是--找直接后继替换
if (del->_pSub[0] != nullptr) //任何时刻叶子节点的孩子一定全为空,非叶子节点的孩子一定全不为空,所以只需要判断第一个孩子是否为空就行了
{
//直接后继节点替代
PNode pCur = del->_pSub[delIdx + 1];
PNode parent = del;
while (pCur)
{
parent = pCur;
pCur = pCur->_pSub[0];
}
del->_keys[delIdx] = parent->_keys[0]; //数据替换
del = parent;
delIdx = 0;
}
while (true)
{
//删除目标删除节点--叶子节点/父节点
_Erase(del, delIdx);
//判断是否会下溢出
//没有下溢出--直接结束
if (del->_size >= _floor || del == _pRoot)
{
return true;
}
//发生下溢出
PNode leftBro = nullptr;
PNode rightBro = nullptr;
int leftParentKeyIdx = -1;
int rightParentKeyIdx = -1;
for (int i = 0; i <= del->_pParent->_size; ++i)
{
if (del->_pParent->_pSub[i] == del)
{
if (i - 1 >= 0)
{
leftBro = del->_pParent->_pSub[i - 1];
leftParentKeyIdx = i - 1;
}
if (i + 1 <= del->_pParent->_size)
{
rightBro = del->_pParent->_pSub[i + 1];
rightParentKeyIdx = i;
}
break;
}
}
//兄弟够借:借 -- 之后直接结束
if (leftBro != nullptr && leftBro->_size > _floor)
{
//父下来头插
for (int i = del->_size; i > 0; i--)
{
del->_keys[i] = del->_keys[i - 1];
//del->_pSub[i + 1] = del->_pSub[i];
}
del->_keys[0] = del->_pParent->_keys[leftParentKeyIdx];
//兄上去
del->_pParent->_keys[leftParentKeyIdx] = leftBro->_keys[leftBro->_size - 1];
if (leftBro->_pSub[leftBro->_size]) //如果右孩子存在要旋转转移
{
for (int i = del->_size + 1; i > 0; i--)
del->_pSub[i] = del->_pSub[i - 1];
del->_pSub[0] = leftBro->_pSub[leftBro->_size];
del->_pSub[0]->_pParent = del;
}
++del->_size;
--leftBro->_size;
return true;
}
else if (rightBro != nullptr && rightBro->_size > _floor)
{
//父下来尾插
del->_keys[del->_size] = del->_pParent->_keys[rightParentKeyIdx];
//兄上去
del->_pParent->_keys[rightParentKeyIdx] = rightBro->_keys[0];
if (rightBro->_pSub[0])
{
del->_pSub[del->_size + 1] = rightBro->_pSub[0];
del->_pSub[del->_size + 1]->_pParent = del;
}
//兄弟节点数据覆盖
for (int i = 1; i < rightBro->_size; i++)
{
rightBro->_keys[i - 1] = rightBro->_keys[i];
rightBro->_pSub[i - 1] = rightBro->_pSub[i];
}
rightBro->_pSub[rightBro->_size - 1] = rightBro->_pSub[rightBro->_size];
++del->_size;
--rightBro->_size;
return true;
}
//兄弟不够借:合并 -- 之后转换为父节点删除操作
else
{
//m个节点,第1~m-1个节点使用父下来到下溢出节点,右边兄弟并过来到下溢出节点
// 第m个节点使用父下来到左边兄弟,下溢出节点并过去到左节点
// 如果下溢出节点是它父节点的最后一个节点(第m)
//if (del == del->_pParent->_pSub[del->_pParent->_size])
if (rightBro == nullptr)
{
PNode tmp = del;
del = leftBro;
rightBro = tmp;
rightParentKeyIdx = leftParentKeyIdx;
}
//父下移到左--尾插
del->_keys[del->_size++] = del->_pParent->_keys[rightParentKeyIdx];
//右边兄弟并过来
for (int i = 0; i < rightBro->_size; i++)
{
del->_keys[del->_size] = rightBro->_keys[i];
if (rightBro->_pSub[i])
{
del->_pSub[del->_size] = rightBro->_pSub[i];
del->_pSub[del->_size]->_pParent = del;
}
++del->_size;
}
if (rightBro->_pSub[rightBro->_size])
{
del->_pSub[del->_size] = rightBro->_pSub[rightBro->_size];
del->_pSub[del->_size]->_pParent = del;
}
//删除父节点指定数据
PNode tmp = del;
del = del->_pParent;
delIdx = rightParentKeyIdx;
//如果删除节点是根节点,更新根节点
if (del == _pRoot && del->_size == 1)
{
_pRoot = tmp;
delete del->_pSub[del->_size];
delete del;
return true;
}
//goto while() _Erase(del, delIdx);
}
}
return true;
}
//void InOrder()
//{
// _InOrder(_pRoot);
//}
//vector<int> _testV;
private:
PNode _pRoot;
const int _floor; //一个节点最少元素个数
};
}