【速写】优化的深度与广度（Adam & Moun）

文章目录

Moun（纳什的部分）
- [Gradient Whitten](#Gradient Whitten)

Adam与AdamW的本质区别在于解耦了正则项，后者使得正则项的梯度步长与自适应步长无关，恒定为 η λ \eta\lambda ηλ：

Adam（Adaptive Moment Estimation）和 AdamW（Adam with Weight Decay）是深度学习中广泛使用的两种优化器，它们的核心区别在于权重衰减（Weight Decay）的实现方式，这对模型训练的正则化效果和泛化性能有显著影响。以下是详细对比：

权重衰减的处理方式

Adam
- 问题：将权重衰减（L2正则化）直接合并到梯度中，与自适应学习率耦合。
  
  更新公式中的权重衰减项：
  θ t = θ t − 1 − η ⋅ m ^ t v ^ t + ϵ − η λ θ t − 1 \theta_t = \theta_{t-1} - \eta \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}t} + \epsilon} - \eta \lambda \theta{t-1} θt=θt−1−η⋅v^t +ϵm^t−ηλθt−1
  
  （其中 λ \lambda λ 是衰减系数， m ^ t \hat{m}_t m^t 和 v ^ t \hat{v}_t v^t 是偏差校正后的梯度一阶矩和二阶矩）
- 缺点：
  - 自适应学习率（如 1 / v ^ t 1/\sqrt{\hat{v}_t} 1/v^t ）会缩放权重衰减的强度，导致衰减效果不稳定。
  - 实际衰减量受梯度大小影响，可能偏离设计意图。
AdamW
- 改进：将权重衰减与梯度计算解耦，独立作用于参数。
  
  更新公式：
  θ t = θ t − 1 − η ( m ^ t v ^ t + ϵ + λ θ t − 1 ) \theta_t = \theta_{t-1} - \eta \left( \frac{\hat{m}_t}{\sqrt{\hat{v}t} + \epsilon} + \lambda \theta{t-1} \right) θt=θt−1−η(v^t +ϵm^t+λθt−1)
  
  或等价形式：
  θ t = ( 1 − η λ ) θ t − 1 − η ⋅ m ^ t v ^ t + ϵ \theta_t = (1 - \eta \lambda) \theta_{t-1} - \eta \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon} θt=(1−ηλ)θt−1−η⋅v^t +ϵm^t
- 优点：
  - 权重衰减始终按固定比例 η λ \eta \lambda ηλ 作用，与自适应学习率无关，更符合正则化设计初衷。
  - 实验表明能显著提升模型泛化能力（如在图像分类、Transformer模型中）。

本质上 m t m_t mt和 v t v_t vt都是历史上所有梯度 g 0 , . . . , g t g_0,...,g_t g0,...,gt的加权和，权重是EMA（指数移动平均）确定的，分别受控于参数 β 1 \beta_1 β1和 β 2 \beta_2 β2， β i \beta_i βi越大则受历史梯度影响越大。

实际效果对比

特性	Adam	AdamW
权重衰减作用时机	与梯度合并，受学习率自适应影响	独立于梯度，直接作用于参数
正则化稳定性	不稳定（衰减量随梯度变化）	稳定（衰减量仅依赖 η λ \eta \lambda ηλ）
泛化性能	较差（尤其在大模型或复杂任务中）	更优
超参数敏感性	对 λ \lambda λ 敏感	对 λ \lambda λ 鲁棒性更强

为什么 AdamW 更优？
- 解耦设计：权重衰减作为纯粹的正则化项，不与自适应学习率相互干扰。
- 对齐 SGD 的 L2 正则化：AdamW 的衰减方式与 SGD with Weight Decay 一致，而 Adam 实际是一种混合形式。
- 实验验证：在 Transformer、ResNet 等模型中，AdamW 通常能达到更低测试误差（如 BERT 训练中 AdamW 是标准选择）。

代码实现

python 复制代码

# Adam（权重衰减合并到梯度）
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, weight_decay=0.01)

# AdamW（权重衰减独立）
optimizer = torch.optim.AdamW(model.parameters(), lr=0.001, weight_decay=0.01)

如何选择？
- 选择 AdamW：当需要严格的 L2 正则化效果时（如训练 Transformer、大规模 CNN）。
- 选择 Adam：仅在历史代码兼容性或特定场景（如某些 GAN 训练）中考虑。

AdamW 因其更合理的权重衰减实现，已成为当前深度学习中的默认优化器选择。

Moun（纳什的部分）

极致的工程优化。

resources
- https://kellerjordan.github.io/posts/muon/
- https://github.com/KellerJordan/cifar10-airbench
a type of second-order optimizer
New "Muon" optimizer: Trains AI language models faster, using less data.
- Pareto frontier
"Muon" excels at training AI efficiently with very large data batches.
"Telescoping"(伸缩) algorithm: Smartly finds optimal AI settings much faster.
- weight decay, learning rate
nats
- ln ⁡ \ln ln：以 e 为底（香浓熵以 2 为底）
- 1.3： L o s s = − ln ⁡ ( p c o r r e c t ) Loss = -\ln(p_{correct}) Loss=−ln(pcorrect)
  - p correct = e − 1.3 p_\text{correct} = e^{-1.3} pcorrect=e−1.3 = 27.25%
And for an empirically-flavored motivation, we observe that based on manual inspection, the updates produced by both SGD-momentum and Adam for the 2D parameters in transformer-based neural networks typically have very high condition number . That is, they are almost low-rank matrices, with the updates for all neurons being dominated by just a few directions. We speculate that orthogonalization effectively increases the scale of other "rare directions" which have small magnitude in the update but are nevertheless important for learning.
- 神经网络中2D参数的更新通常具有非常高的条件数。也就是说，它们几乎是低秩矩阵，所有神经元的更新都被少数几个方向主导。"
- 正交化会"有效地增加其他'稀有方向'的尺度"。这意味着，尽管次要任务的原始梯度信号很弱，但在正交化之后，这个方向在最终的 update 矩阵中会被放大，其重要性得到提升。

When training a neural network with Muon, scalar and vector parameters of the network (bias, head), as well as the input and output layers, should be optimized by a standard method such as AdamW. Muon can be used for 4D convolutional parameters by flattening their last three dimensions.

Muon is an optimizer for 2D parameters of neural network hidden layers.
And for an empirically-flavored motivation, we observe that based on manual inspection, the updates produced by both SGD-momentum and Adam for the 2D parameters in transformer-based neural networks typically have very high condition number . That is, they are almost low-rank matrices, with the updates for all neurons being dominated by just a few directions. We speculate that orthogonalization effectively increases the scale of other "rare directions" which have small magnitude in the update but are nevertheless important for learning.
- 神经网络中2D参数的更新通常具有非常高的条件数。也就是说，它们几乎是低秩矩阵，所有神经元的更新都被少数几个方向主导。
- 正交化会"有效地增加其他'稀有方向'的尺度"。这意味着，尽管次要任务的原始梯度信号很弱，但在正交化之后，这个方向在最终的 update 矩阵中会被放大，其重要性得到提升。
When training a neural network with Muon, scalar and vector parameters of the network, as well as the input and output layers, should be optimized by a standard method such as AdamW. Muon can be used for 4D convolutional parameters by flattening their last three dimensions.
- Muon 的核心是"白化"梯度，即抹去梯度的大小（奇异值），只保留其方向。
- 对于输出层，我们希望模型能够学习到不同特征对于最终分类的重要性。例如，某个从卷积层提取的特征可能对识别"猫"至关重要，而对识别"汽车"无关紧要。这种重要性会体现在梯度的尺度上，从而让优化器（如SGD或Adam）大幅调整对应的权重。
- 输入层：权重不被训练: 请注意代码中的 self.whiten.weight.requires_grad = False。它的权重是通过 init_whiten 函数，利用训练数据的统计特性（协方差矩阵）一次性计算出来的（这是一种ZCA白化），之后就被冻结，不参与反向传播和梯度更新。既然没有梯度，自然也谈不上用任何优化器去优化它。
- 偏置项 (Bias) 是向量: 输入层唯一需要学习的参数是它的偏置项 self.whiten.bias，这是一个向量。Muon 是为2D矩阵设计的，不适用于向量。因此，这个偏置项也被交给了SGD优化器处理。
Muon (MomentUm Orthogonalized by Newton-Schulz) optimizes 2D neural network parameters by taking the updates generated by SGD-momentum, and then applying a Newton-Schulz (NS) iteration as a post-processing step to each of them before applying them to the parameters.
orthogonal matrix: Q T Q = I Q^TQ=I QTQ=I
- 几何上刻画旋转（rotation）和反射（reflection）
  - det(Q) = 1，表示旋转
    - Q = ( 0 − 1 1 0 ) Q= \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} Q=(01−10)
      - (1, 0) => (0, 1)
  - det(Q) = -1，则表示反射
    - Q = ( − 1 0 0 1 ) Q = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} Q=(−1001)
      - (x, y) => (-x, y)
    - Q = ( 1 0 0 0 − 1 0 0 0 1 ) Q = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} Q= 1000−10001
      - (x, y, z) => (x, -y, z)
矩阵的 0 次幂（zeroth power）
- 奇异值分解（SVD）中的正交部分
zeropower_via_newtonschulz5（3次五次多项式迭代，快速地计算出梯度矩阵的近似正交部分（UV^T），实现梯度的白化）
- zeropower: 计算矩阵的零次幂。
- via_newtonschulz: 通过"牛顿-舒尔茨（Newton-Schulz）"迭代算法来实现。这是一种避免直接进行昂贵的SVD分解的数值方法。
- 5: 指的是迭代中使用了一个五次（quintic）多项式。
sgd vs. netwon vs. Muon
- sgd: w − η ⋅ g w - \eta \cdot g w−η⋅g
- netwon: w − η ⋅ H − 1 g w - \eta \cdot H^{-1} g w−η⋅H−1g
- Muon: w − η ⋅ zeropower ( g ) w - \eta \cdot \text{zeropower}(g) w−η⋅zeropower(g)

Gradient Whitten

在标准的梯度下降中，我们沿着负梯度方向更新权重。但如果梯度的各个维度之间相关性很高，或者尺度差异很大，优化过程就会很慢。
"白化"变换旨在解耦 (decorrelate) 梯度的各个维度，并将其尺度归一化 (normalize scale)，使得优化路径更直接、高效。

任何一个矩阵 G 都可以进行奇异值分解（SVD）：
G = U S V T G = U S V^T G=USVT

U 和 V 是正交矩阵（Orthogonal Matrices）。它们的列向量是标准正交的。
S 是一个对角矩阵，对角线上的值是奇异值（Singular Values），表示了 G 在各个主方向上的"拉伸"或"缩放"程度。
SVD 几何上的意义
- V T V^T VT：一次旋转/反射
- S S S：沿着新的坐标轴进行缩放（拉伸或压缩）。奇异值就是缩放的比例。
- U U U：另一次旋转/反射。

矩阵 G 的"零次幂" G^0 在这里的定义是
G 0 = U S 0 V T G^0 = U S^0 V^T G0=US0VT

其中 S 0 S^0 S0 是将 S 的所有非零对角元（奇异值）都替换为1得到的对角矩阵。因此，最终结果是：

G 0 = U I V T = U V T G^0 = U I V^T = UV^T G0=UIVT=UVT

这个 U V T UV^T UVT 矩阵是一个正交矩阵（ ( U V T ) ( V U T ) = I (UV^T)(VU^T)=I (UVT)(VUT)=I），它保留了原始矩阵 G 的"旋转"或"方向"信息，但完全丢弃了其"缩放"或"大小"的信息（因为所有奇异值都变成了1）。在信号处理和机器学习中，这个过程被称为白化（Whitening），因为它使得变换后的数据在各个方向上的方差都相等（均为1）。数学上的意义：

正交矩阵代表一种保距变换（Isometry），比如旋转（Rotation）或反射（Reflection）。它在对向量进行变换时，不会改变向量的长度，也不会改变向量之间的夹角。它只改变方向。
它的所有列向量（和行向量）构成一组标准正交基（Orthonormal Basis）。也就是说，每个列向量的长度都是1，且任意两个不同的列向量都相互垂直（点积为0）。

Moun源码中的SVD白化实现：

python 复制代码

@torch.compile
def zeropower_via_newtonschulz5(G, steps=3, eps=1e-7):
    """
    Newton-Schulz iteration to compute the zeroth power / orthogonalization of G.
    """
    assert len(G.shape) == 2
    a, b, c = (3.4445, -4.7750,  2.0315)
    X = G.bfloat16()
    X /= (X.norm() + eps) # ensure top singular value <= 1
    if G.size(0) > G.size(1):
        X = X.T
    for _ in range(steps):
        A = X @ X.T
        B = b * A + c * A @ A
        X = a * X + B @ X
    if G.size(0) > G.size(1):
        X = X.T
    return X.float() # 返回 float 方便对比

这里很经典的三个常量a, b, c是三个经验值

python 复制代码

X /= (X.norm() + eps) # ensure top singular value <= 1

矩阵的 Frobenius Norm （F范数）总是大于或等于其谱范数（Spectral Norm，即最大奇异值）。
- 对于矩阵 X X X 奇异值假设为 σ 1 , σ 2 , ⋯ , σ r \sigma_1,\sigma_2, \cdots, \sigma_r σ1,σ2,⋯,σr（降序排列 σ 1 ≥ σ 2 ≥ ⋯ ≥ σ r ≥ 0 \sigma_1 \ge \sigma_2 \ge \dots \ge \sigma_r \ge 0 σ1≥σ2≥⋯≥σr≥0）
- 谱范数： ∣ ∣ X ∣ ∣ 2 = σ m a x = σ 1 ||X||2 = \sigma{max} = \sigma_1 ∣∣X∣∣2=σmax=σ1
  - ∣ ∣ X ∣ ∣ 2 2 = σ 1 2 ||X||_2^2 = \sigma_1^2 ∣∣X∣∣22=σ12
- F范数： ∣ ∣ X ∣ ∣ F = ∑ i = 1 m ∑ j = 1 n ∣ x i j ∣ 2 = ∑ k = 1 r σ k 2 ||X||F = \sqrt{\sum{i=1}^m \sum_{j=1}^n |x_{ij}|^2} = \sqrt{\sum_{k=1}^r \sigma_k^2} ∣∣X∣∣F=∑i=1m∑j=1n∣xij∣2 =∑k=1rσk2
  - ∣ ∣ X ∣ ∣ F 2 = σ 1 2 + σ 2 2 + ⋯ + σ r 2 ||X||_F^2 = \sigma_1^2 + \sigma_2^2 + \dots + \sigma_r^2 ∣∣X∣∣F2=σ12+σ22+⋯+σr2
- ∣ ∣ X ∣ ∣ F 2 ≥ ∣ ∣ X ∣ ∣ 2 2 ||X||_F^2 \ge ||X||_2^2 ∣∣X∣∣F2≥∣∣X∣∣22
torch.norm: defaut fro
- X_norm = X / X.norm()
  - ∣ ∣ X n o r m ∣ ∣ 2 = ∣ ∣ 1 ∣ ∣ X ∣ ∣ F ⋅ X ∣ ∣ 2 = 1 ∣ ∣ X ∣ ∣ F ⋅ ∣ ∣ X ∣ ∣ 2 ≤ 1 ∣ ∣ X ∣ ∣ F ⋅ ∣ ∣ X ∣ ∣ F = 1 ||X_{norm}||_2 = ||\frac{1}{||X||_F} \cdot X||_2 = \frac{1}{||X||_F} \cdot ||X||_2 \leq \frac{1}{||X||_F} \cdot ||X||_F=1 ∣∣Xnorm∣∣2=∣∣∣∣X∣∣F1⋅X∣∣2=∣∣X∣∣F1⋅∣∣X∣∣2≤∣∣X∣∣F1⋅∣∣X∣∣F=1
其他范数
- 核范数（nuclear norm）
  - ∣ ∣ X ∣ ∣ ∗ = ∑ k = 1 r σ k = σ 1 + σ 2 + ⋯ + σ r ||X||* = \sum{k=1}^r \sigma_k = \sigma_1 + \sigma_2 + \dots + \sigma_r ∣∣X∣∣∗=∑k=1rσk=σ1+σ2+⋯+σr
  - 矩阵的迹 (Trace) 是其对角线元素之和，也等于其所有特征值 (Eigenvalues) 之和。
  - 矩阵的核范数 (Nuclear Norm) 是其所有奇异值 (Singular Values) 之和。
  - 对于一个半正定矩阵 X T X X^T X XTX，它的奇异值和特征值是相同的。核范数的严格定义是 ∣ ∣ X ∣ ∣ ∗ = Tr ( X T X ) ||X||_* = \text{Tr}(\sqrt{X^T X}) ∣∣X∣∣∗=Tr(XTX )，即矩阵 ( X T X ) 1 / 2 (X^T X)^{1/2} (XTX)1/2 的迹；

这里是代码示例：

python 复制代码

torch.manual_seed(123)
rows, cols = 4, 6
X = torch.randn(rows, cols) * 10 
X_f = X.norm()
X_f # tensor(46.1010)

sigmas = torch.linalg.svdvals(X)
sigmas tensor([33.6294, 25.1017, 16.3428,  9.8583])

top_sigma = sigmas[0]
top_sigma # tensor(33.6294)

torch.sqrt(torch.sum(torch.linalg.svdvals(X) ** 2)) # tensor(46.1010)

X_norm = X / X_f
torch.linalg.svdvals(X_norm) # tensor([0.7295, 0.5445, 0.3545, 0.2138])

# spectral_norm
torch.linalg.norm(X, ord=2) # tensor(33.6294)

torch.linalg.norm(X, ord='nuc') # tensor(84.9322)

torch.sum(torch.linalg.svdvals(X)) # tensor(84.9322)

python 复制代码

if G.size(0) > G.size(1):
    X = X.T

通过将"瘦高"的矩阵转置为"矮胖"的矩阵，可以确保 X @ X.T 是两个可能方阵中较小的那一个，从而减少计算量。

python 复制代码

a, b, c = (3.4445, -4.7750,  2.0315)
for _ in range(steps):
    A = X @ X.T
    B = b * A + c * A @ A
    X = a * X + B @ X

X k + 1 = ( a I + b ( X k X k T ) + c ( X k X k T ) 2 ) X k X_{k+1} = (aI + b(X_k X_k^T) + c(X_k X_k^T)^2) X_k Xk+1=(aI+b(XkXkT)+c(XkXkT)2)Xk
- 这个迭代过程实际上是在对 X X X 的奇异值 s s s 应用一个多项式函数 f ( s ) f(s) f(s)， s k + 1 = s k ⋅ ( a + b ⋅ s k 2 + c ⋅ s k 4 ) s_{k+1} = s_k \cdot (a + b \cdot s_k^2 + c \cdot s_k^4) sk+1=sk⋅(a+b⋅sk2+c⋅sk4)
  - X = U S V T X=USV^T X=USVT
  - X X T = U S ( V T V ) S T U T = U S I S T U T = U ( S S T ) U T = U S 2 U T X X^T = U S (V^T V) S^T U^T = U S I S^T U^T = U (S S^T) U^T=US^2U^T XXT=US(VTV)STUT=USISTUT=U(SST)UT=US2UT
  - S S S 是一个对角矩阵，所以 S S T S S^T SST 也是一个对角矩阵，其对角线上的元素是原始奇异值的平方 s i 2 s_i^2 si2
- 这是一个关于 s k s_k sk 的五次多项式（quintic），这些系数 a, b, c 的选择目标是让这个函数 f ( s ) f(s) f(s) 能够快速地将 (0, 1] 区间内的所有值都推向 1。
  - 经过 steps 次迭代后，X 的所有奇异值都会非常接近1，从而使得 X 近似于其正交部分 UV^T。

s n e w = f ( s ) = s ⋅ ( a + b ⋅ s 2 + c ⋅ s 4 ) s_{new} = f(s) = s \cdot (a + b \cdot s^2 + c \cdot s^4) snew=f(s)=s⋅(a+b⋅s2+c⋅s4)

python 复制代码

a, b, c = (3.4445, -4.7750,  2.0315)
f = lambda s: s * (a + b * s**2 + c*s**4)
s = 0.7
s = f(s)
s # 1.114759205
s = f(s)
s # 0.7222038499421772
s = f(s)
s # 1.0880871827296072
s = f(s)
s # 0.6950353973496508
s = f(s)
s # 1.1203226304932916

多次迭代后会越来越接近1

对比传统SVD呢？

python 复制代码

def zeropower_via_svd(G):
    """
    Computes the zeroth power G^0 = UV^T using direct SVD.
    This is mathematically exact but computationally expensive.
    """
    # full_matrices=False 更高效，因为我们不需要完整的 U 或 V
    U, S, Vh = torch.linalg.svd(G, full_matrices=False)
    # G^0 = U @ Vh (因为 Vh 已经是 V.T)
    return U @ Vh

torch.manual_seed(42)
device = "cuda" if torch.cuda.is_available() else "cpu"

rows, cols = 256, 1024
G = torch.randn(rows, cols, device=device)

def diff(G, steps=3):
    exact_result = zeropower_via_svd(G)
    approx_result = zeropower_via_newtonschulz5(G, steps=steps)
    frobenius_diff = torch.norm(exact_result - approx_result)
    cosine_sim = F.cosine_similarity(exact_result.flatten(), approx_result.flatten(), dim=0)
    print(f'frobenius_diff: {frobenius_diff}, cos_sim: {cosine_sim}')
    s_exact = torch.linalg.svdvals(exact_result)
    s_approx = torch.linalg.svdvals(approx_result)
    print("\n   For the EXACT (SVD) result:")
    print(f"   - All singular values should be 1.0")
    print(f"   - Min: {s_exact.min().item():.4f}, Max: {s_exact.max().item():.4f}, Mean: {s_exact.mean().item():.4f}")
    print("\n   For the APPROXIMATE (Newton-Schulz) result:")
    print(f"   - Singular values should be scattered around 1.0")
    print(f"   - Min: {s_approx.min().item():.4f}, Max: {s_approx.max().item():.4f}, Mean: {s_approx.mean().item():.4f}")

diff(G, steps=3)

输出结果：

python 复制代码

frobenius_diff: 2.364572763442993, cos_sim: 0.9932388067245483

   For the EXACT (SVD) result:
   - All singular values should be 1.0
   - Min: 1.0000, Max: 1.0001, Mean: 1.0001

   For the APPROXIMATE (Newton-Schulz) result:
   - Singular values should be scattered around 1.0
   - Min: 0.7570, Max: 1.2046, Mean: 1.0774

具体在MounOpt中的应用：

python 复制代码

update = zeropower_via_newtonschulz5(g.reshape(len(g), -1)).view(g.shape) # whiten the update
p.data.add_(update, alpha=-lr) # take a step

传统的SGD优化器会沿着梯度 g 的方向更新参数：p.data.add_(g, alpha=-lr)。
Muon 优化器不同，它首先对梯度 g 进行"白化"，得到 update，然后沿着这个白化后的方向进行更新。update 矩阵保留了梯度的"方向"，但其"尺度"被归一化了。这可以：
- 解决梯度尺度不一的问题：不同层的梯度大小可能差异巨大，白化可以使更新步长更加均衡。
- 改善优化路径：通过解耦参数更新的方向和大小，可能找到更优的收敛路径，类似于二阶优化方法（如牛顿法）所做的事情，但计算成本低得多。
Muon 的战场是"矩阵"，而非"向量"：Muon 专为神经网络中二维的参数矩阵（如 nn.Linear 层的权重）而设计。它的核心 zeropower / NewtonSchulz5 操作是对一个矩阵进行正交化。
Muon 解决的是"几乎低秩"的更新问题：博客中提到一个关键洞察："...transformer-based neural networks typically have very high condition number. That is, they are almost low-rank matrices, with the updates for all neurons being dominated by just a few directions." 这意味着，在真实的神经网络训练中，梯度更新矩阵 G 的大部分"能量"都集中在少数几个奇异值上。SGD 会被这几个主要方向带着跑，而忽略了那些虽然奇异值小但对学习同样重要的"稀有方向"（rare directions）。
Muon 的策略是"重新加权"而非简单"归一化"：zeropower 的正交化操作，相当于将梯度矩阵 G 的所有奇异值都强行置为1（近似地）。这极大地提升了那些"稀有方向"的权重，让优化器能够同时在所有方向上学习，而不是只被几个主导方向所困。

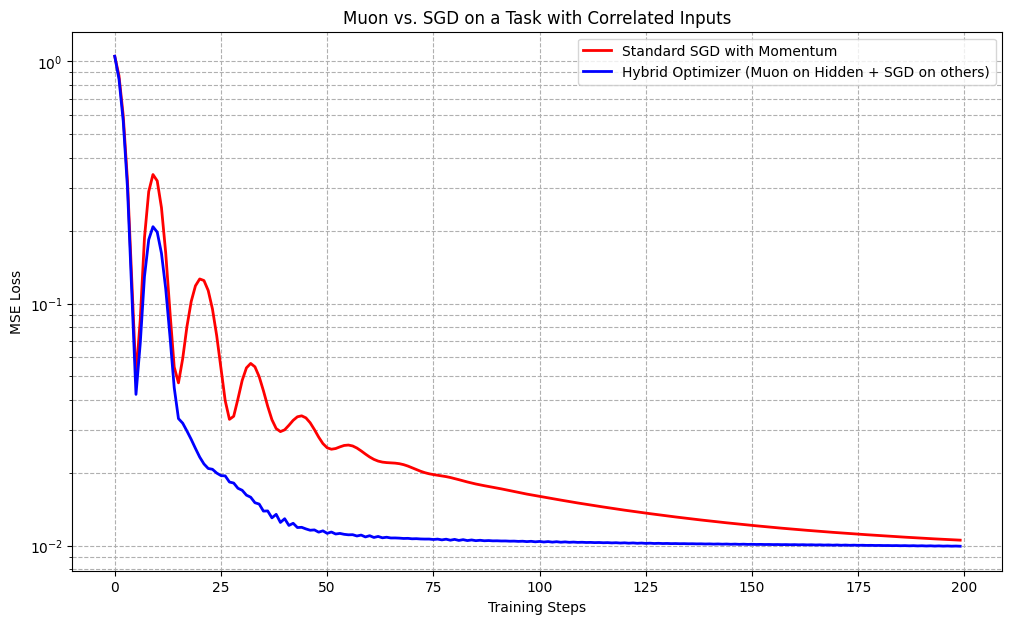
最后看一个Moun与SGD优化的loss对比：

python 复制代码

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np

# --- 从 airbench94_muon.py 脚本中复制过来的核心函数 ---
def zeropower_via_newtonschulz5(G, steps=5, eps=1e-7):
    assert G.ndim == 2
    a, b, c = (3.4445, -4.7750,  2.0315)
    X = G.float()
    X /= (X.norm() + eps)
    if G.size(0) > G.size(1):
        X = X.T
    for _ in range(steps):
        A = X @ X.T
        B = b * A + c * A @ A
        X = a * X + B @ X
    if G.size(0) > G.size(1):
        X = X.T
    return X

# --- 自定义 Muon 优化器 (简化版，用于演示) ---
class SimpleMuon(torch.optim.Optimizer):
    def __init__(self, params, lr=1e-3):
        defaults = dict(lr=lr)
        super().__init__(params, defaults)

    def step(self):
        for group in self.param_groups:
            lr = group['lr']
            for p in group['params']:
                if p.grad is None:
                    continue
                g = p.grad.data
                
                # Muon的核心：只对2D矩阵操作
                if g.ndim == 2:
                    update_direction = zeropower_via_newtonschulz5(g)
                    p.data.add_(update_direction, alpha=-lr)
                else: # 对于非矩阵参数，回退到SGD
                    p.data.add_(g, alpha=-lr)

# --- 场景设置 ---
class SimpleMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(2, 16)
        self.output = nn.Linear(16, 1)
    
    def forward(self, x):
        return self.output(torch.relu(self.hidden(x)))

def generate_data(n_samples=512):
    x1 = torch.randn(n_samples, 1) * 2
    # x2 与 x1 高度相关
    x2 = 0.8 * x1 + torch.randn(n_samples, 1) * 0.2
    X = torch.cat([x1, x2], dim=1)
    # 目标是学习一个需要区分 x1 和 x2 的函数
    y = x1 - 0.5 * x2 + torch.randn(n_samples, 1) * 0.1
    return X, y

def train(optimizer_name):
    torch.manual_seed(42)
    model = SimpleMLP()
    X_train, y_train = generate_data()
    loss_fn = nn.MSELoss()
    
    if optimizer_name == 'sgd':
        optimizer = torch.optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
    elif optimizer_name == 'muon_hybrid':
        # 严格按照博客建议：只对隐藏层权重使用Muon
        muon_params = [model.hidden.weight]
        sgd_params = [p for p in model.parameters() if id(p) not in [id(model.hidden.weight)]]
        
        optimizer = torch.optim.SGD([
            {'params': muon_params, 'lr': 0.05, 'is_muon': True}, # 标记为Muon参数
            {'params': sgd_params, 'lr': 0.01, 'momentum': 0.9}
        ])

    loss_history = []
    for i in range(200):
        optimizer.zero_grad()
        y_pred = model(X_train)
        loss = loss_fn(y_pred, y_train)
        loss.backward()

        # --- 自定义优化步骤以处理混合优化器 ---
        if optimizer_name == 'muon_hybrid':
            with torch.no_grad():
                for group in optimizer.param_groups:
                    lr = group['lr']
                    if group.get('is_muon', False):
                        # 这是 Muon 部分
                        for p in group['params']:
                            if p.grad is not None:
                                update = zeropower_via_newtonschulz5(p.grad.data)
                                p.data.add_(update, alpha=-lr)
                    else:
                        # 这是 SGD 部分
                        for p in group['params']:
                            if p.grad is not None:
                                # 手动实现SGD+Momentum
                                param_state = optimizer.state[p]
                                if 'momentum_buffer' not in param_state:
                                    buf = param_state['momentum_buffer'] = torch.clone(p.grad.data).detach()
                                else:
                                    buf = param_state['momentum_buffer']
                                    buf.mul_(group['momentum']).add_(p.grad.data, alpha=1)
                                p.data.add_(buf, alpha=-lr)
        else:
            optimizer.step()
            
        loss_history.append(loss.item())
        
    return loss_history

绘图：

python 复制代码

loss_sgd = train('sgd')
loss_muon = train('muon_hybrid')

plt.figure(figsize=(12, 7))
plt.plot(loss_sgd, label='Standard SGD with Momentum', color='red', linewidth=2)
plt.plot(loss_muon, label='Hybrid Optimizer (Muon on Hidden + SGD on others)', color='blue', linewidth=2)
plt.xlabel('Training Steps')
plt.ylabel('MSE Loss')
plt.yscale('log')
plt.title('Muon vs. SGD on a Task with Correlated Inputs')
plt.legend()
plt.grid(True, which="both", ls="--")
# plt.show()