【论文精度-2】求解车辆路径问题的神经组合优化算法:综合展望（Yubin Xiao，2025）

论文地址：

https://arxiv.org/abs/2406.00415https://arxiv.org/abs/2406.00415

部分	内容概述	重点关键词
I. 引言 (Introduction)	提出研究背景：VRP 在现实世界的复杂性；传统 OR 方法的局限；NCO 的出现。	VRP、NCO、挑战、研究动机
II. 背景与基础 (Preliminaries)	介绍 VRP 及其常见变体（TSP、CVRP 等）与传统 OR 求解思路，为后文奠基。	OR 方法、TSP/CVRP、约束
III. NCO 的学习框架与方法分类 (Taxonomy of NCO Solvers)	提出本文的核心分类体系：L2C、L2I、L2P-O、L2P-M 四类求解器；说明它们的差异。	Learning to Construct / Improve / Predict
IV. 各类 NCO 求解器分析 (Comparative Review)	对四类求解器分别讲解结构、原理、代表方法与性能表现。	L2C、L2I、L2P-O、L2P-M
V. 比较性能与趋势分析 (Performance and Trends)	用实验结果对比不同求解器在 TSP/CVRP 等基准任务上的性能（Gap、Time）。	Gap、最优解、最强 OR 对比
VI. 现存问题与改进方向 (Challenges and Improvements)	分析当前 NCO 的三大不足：① 泛化能力不足② 无法高效处理大规模 VRP③ 多约束变体表现差并提出相应改进方向。	泛化、分布、分解、MTL、混合求解
VII. 结论与展望 (Conclusion)	总结本文贡献，提出未来研究方向与跨领域价值（ML 与 OR 的融合）。	通用框架、混合范式、研究前景

📘 整篇文章的逻辑主线：

从传统 VRP → NCO 出现 → 四类方法分类 → 性能分析 → 不足与改进 → 未来融合发展

可以概括为：

"问题提出 → 方法体系 → 性能评估 → 挑战分析 → 未来展望"

类别	是否独立求解	神经网络预测频率	时间效率（速度）	解质量（接近最优）	代表性方法	典型优势	主要瓶颈
L2C(Learning to Construct)	✅ 端到端生成	每步一次（构建过程中）	🟢 最快推理（一次前向生成即得解）	🟡 中等偏上（通过后处理可逼近最优）	PointerNet, AM, POMO	推理快、可并行	泛化差，对约束问题效果弱
L2I(Learning to Improve)	✅ 独立优化	每次迭代一次	🟡 较慢（多步强化迭代）	🟢 较高（逐步改良）	NeuRewriter, N2OPT, NeuOPT	可持续改进、解质量高	时间成本高，收敛慢
L2P-O(Learning to Predict Once)	❌ 辅助 OR	仅在开始预测一次	🟢 显著提速（缩小搜索空间）	🟢 高（OR 决策主导）	DPDP, DeepACO, DP-GNN	快、稳、解质量好	需训练预测模型，泛化仍有限
L2P-M(Learning to Predict Multiple)	❌ 深度协同 OR	每步多次预测	🔴 最慢（每步调用 NN）	🟢 最优或接近最优	RL-LKH, NDP, LLM-based Heuristic	动态引导、最强性能潜力	计算代价大，实现复杂

解质量 ↑

│

│ ● L2P-M （最优质量，时间长）

│ ●

│ ● L2P-O

│ ● L2I

│● L2C

│

└────────────────────────────→ 时间开销

快（低）慢（高）

对比方向	论文结论
L2C vs L2I	L2C 适合实时快速求解；L2I 适合需要多次优化、解质量更高的场景。
L2P-O vs L2P-M	L2P-O 注重一次预测的高效协助；L2P-M 注重全过程引导，性能最优但耗时最大。
综合取舍	若追求速度 → L2C / L2P-O；若追求精度 → L2I / L2P-M。
工业落地建议	中小规模/实时调度：L2C 或 L2P-O；大规模/高精度规划：L2P-M；周期性改良任务：L2I。

解决泛化问题：

方法	主要针对问题	机制	泛化改善点	计算代价
多分布训练	分布变化	数据多样化	学习分布共性	中等
课程学习	分布复杂度递增	学习曲线平滑	稳定收敛	较低
知识蒸馏	跨分布综合	多教师融合	提取普适知识	中等偏高
元学习	跨任务（分布+规模）	快速适应机制	泛化 + 迁移	较高
不变性学习	局部结构稳定性	结构建模	抗分布变化	低
熵缩放	注意力自适应	参数调整	轻量泛化增强	极低

解决大规模vrp的不足：

⚙️ 二、自注意力机制的计算瓶颈

📘 背景：

几乎所有现代 NCO 求解器（尤其是 L2C/L2I）都基于 Transformer 或其变体。

Transformer 的核心就是 自注意力（Self-Attention）。

⚙️ 原理简述：

对于一个 N 节点的图（TSP 或 VRP 实例），每个节点有一个 d 维嵌入向量。

定义：

第 i 个节点的注意力计算为：

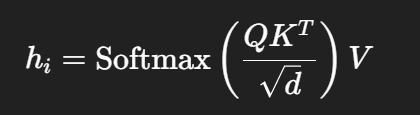
⚠️ 结果：

大规模 TSP/VRP（如 N=1000 或 10000）时显存爆炸；
训练不收敛；
无法实时推理。

🧠 三、解决方案一：分而治之（D&C, Divide and Conquer）

📘 基本思想：

将大问题切分成多个小子问题分别求解，再把子解整合。

这种方法是目前最主流、最有效的扩展手段之一。

⚙️ 实现方式：

划分阶段（Decomposition）：用一个"划分模型"把大图分成多个区域；
求解阶段（Solving）：用 L2C 或 OR 求解器分别解决每个子区域；
整合阶段（Merging）：组合子解得到全局路径。

🧩 代表性研究：

H-TSP [65]：
- 上层模型负责划分；
- 下层使用 L2C 求解子问题；
- 结果提升 1%--10%。
Hou et al. [85]：
- 用 Transformer 做划分；
- 用 LKH3（传统启发式）解每个子问题。

📈 核心挑战：
如何最优地划分 是 D&C 方法的关键。

不当划分会导致边界连接成本大，整体路径变差。

⚙️ 四、解决方案二：轻量化神经网络与改进注意力机制

有研究认为 D&C 只是"拆小"，并没有根治复杂度问题。

因此另一方向是从模型结构入手------让网络本身更轻、更高效。

🧩 代表工作：

方法	改进点	复杂度
Yang et al. [144] (TSPformer)	将传统 "scaled dot-product attention" 改为 "sampled scaled dot-product attention"，通过采样降低计算量	低于 O(N²d)
Xiao et al. [59] (GELD)	提出区域平均线性注意力 (Region Average Linear Attention) 将节点分区，每区平均信息，再进行全局交换	O(Nd)，显著降低复杂度
Luo et al. [39]	用监督学习 (SL) 代替强化学习 (RL) 训练。RL 需生成完整路径计算奖励，内存压力大；SL 只预测下一步，效率高	显著节省显存
Min et al. [73] (UTSP)	用创新的无监督学习 (UL) 损失函数训练 GCN；参数量仅为 SL 模型的 10%，泛化更强	极轻量

⚙️ 五、解决方案三：基于热图的 L2P-O / Diffusion 求解器

这一类方法通过预测 热图（heatmap） 来加速 OR 搜索，不直接生成解。

它们是目前在大规模 TSP 上性能最强的系列。

📘 代表性方法：

模型	核心思路	规模	Gap
UTSP [73]	用 GCN 预测热图 + 搜索构造解	TSP-1000	≈1%
DIFUSCO [48]	基于扩散模型（Diffusion Model），在最优解上不断加入伯努利噪声并学习降噪 → 能预测高质量热图	TSP-10000	2.58%
Fast T2T [209]	优化 DIFUSCO 的多步生成过程，一步生成高质量热图	TSP-10000	同级精度、推理更快

💡 为什么扩散模型有效：

扩散过程让模型学习"扰动---修复"关系；
本质上相当于在"最优解附近"学习局部结构；
能预测更精确的边重要性，从而指导高质量构造。

🚚 六、解决方案四：应对复杂约束的 VRP（如 CVRP）

📘 问题：

TSP 只有路径约束，而 CVRP（带容量限制）更复杂。

→ 纯"热图"方法难以捕捉容量约束。

⚙️ 改进：

建议结合更强的 OR 算法（如 DP、CP、HGS） 进行可行性修正；
Zheng et al. [71] (UDC) 提出：
- 用各向异性 GNN 做全局划分；
- 每个子问题用 L2C 解；
- 综合性能超越 LKH3。

📉 但：

在更复杂的 VRP 变体（如 OVRP）上，性能仍落后 LKH3 约 8.71%。

⚙️ 七、未来方向与建议

论文在最后提出了两条发展思路：

改进方向	理由
使用轻量级 NN 架构（如 Mamba）替代 Transformer	减少注意力层的平方复杂度，提升推理速度与可扩展性
结合 OR 算法进行混合求解	提高对复杂约束（如 CVRP、OVRP）的建模能力
缩小"合成数据 vs 真实数据"性能差距	当前模型在 TSPLib/真实分布上性能下降明显

车辆路由问题变体的不足之处：

1️⃣ 背景：现实中的 VRP 远比 TSP / CVRP 复杂

论文指出，目前大多数 NCO 求解器主要集中在：

TSP（旅行商问题）
CVRP（带容量约束的车辆路径问题）

但现实中的调度任务往往包含多种复杂约束，例如：

多车队、多目标、时间窗、任务优先级、动态客户请求等。

这些都属于 VRP 的变体问题 （Vehicle Routing Problem Variants），

其中最典型的两个是：

缩写	含义	复杂性来源
MOVRP	多目标 VRP（Multi-Objective VRP）	需同时优化多指标（如距离 + 时间 + 能耗）
DVRP	动态 VRP（Dynamic VRP）	客户或订单实时变化，要求快速重规划

2️⃣ 针对多目标 VRP (MOVRP) 的改进方向

多目标问题的本质是：不存在单一最优解，而是一个"帕累托最优集（Pareto Front）"。

论文总结了三类代表性方法👇

🧠 (1) MOEA/D 框架方法

Multi-Objective Evolutionary Algorithm based on Decomposition

把多目标优化问题分解成多个单目标子问题；
每个子问题对应一个独立的求解器；
最终汇总所有子解形成帕累托解集。

📘 优点：稳定、可并行。

📉 缺点：计算量大（要训练多个模型）。

🧠 (2) 偏好条件求解器 (Preference-conditioned Solver)

代表：Lin 等人 [116]

不再用多个模型；
表示对各目标的权重；
求解器根据偏好动态生成不同解；
能逼近整条帕累托前沿（Pareto Front）。

📘 优点：模型复用、一体化；

📉 缺点：学习难度更高，偏好分布设计敏感。

🧠 (3) 图-图像融合 (Graph--Image Dual Modality)

代表：Chen 等人 [216]

将 VRP 的图结构特征（节点、边）与图像式特征（地理布局）结合；
使用双通道网络（Graph + CNN）融合信息；
提升模型对复杂空间约束的感知能力。

📘 含义：让 NCO 同时理解"图拓扑"与"地理空间"，

增强模型在实际交通场景下的可行性。

3️⃣ 针对动态 VRP (DVRP) 的改进方向

动态 VRP 的挑战是：

"客户池"随时间变化（新订单到来、旧订单取消），模型必须实时更新路径。

🧠 (1) 动态节点池机制

代表：Zhang 等人 [125]

模型维护一个可变的节点池；
每次新订单或取消，节点池更新；
然后模型即时更新嵌入表示（embedding）并重新规划路径。

📘 含义：让 L2C 求解器具备 实时自适应性（on-the-fly adaptation）。

🧠 (2) 多约束场景（时间窗 + 实时更新）

例如网约车调度：

要求每个客户必须在规定时间段内服务；
同时订单实时变化；
模型需兼顾"时间窗"和"动态性"双重约束。

📉 难点：

L2C/L2I 这类模型原本是静态优化器，动态更新后稳定性和可行性都会下降。

4️⃣ 多任务学习（MTL）思路：让模型"一次学会多种VRP"

代表性研究：

Liu 等人 [217] ：提出 组合零样本学习 + 多任务学习 (MTL)

→ 将 VRP 表述为一组可组合的约束（如容量、时间窗、优先级）。

模型通过共享网络同时学习多种约束模式。
Zhou 等人 [70] ：引入"混合专家 (Mixture of Experts)"结构，

不同专家处理不同VRP变体，主网络负责任务选择。

📘 优点：提升求解器的通用性 ；

📉 挑战：不同任务的优化目标冲突，训练不稳定。

🧠 冲突缓解策略

子损失权重调整

给每种任务一个动态权重；
混合批训练

每个批次混合不同约束实例；
多变量奖励归一化

让不同任务的奖励值标准化；
元学习（Meta-learning）

自动学习不同任务之间的权重关系。

5️⃣ 当前限制与未来方向

问题	现状	改进方向
规模限制	目前多功能求解器仅能处理 ≤100 节点	提高可扩展性 (如轻量化注意力机制)
分布泛化差	无法适应不同数据分布（真实 vs 合成）	加强跨分布训练 (Domain Adaptation)
多约束学习冲突	子任务目标冲突	元学习动态权重、自适应损失平衡
通用求解器	仅能在 VRP 范畴使用	未来希望扩展到更通用的组合优化问题 (如 VRP + JSP)