LeetCode 74. 搜索二维矩阵

题目描述

给你一个满足下述两条属性的 m x n 整数矩阵：

每行中的整数从左到右按非严格递增顺序排列。
每行的第一个整数大于前一行的最后一个整数。

给你一个整数 target ，如果 target 在矩阵中，返回 true ；否则，返回 false 。

示例

示例 1：

复制代码

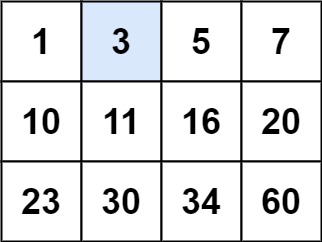
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

复制代码

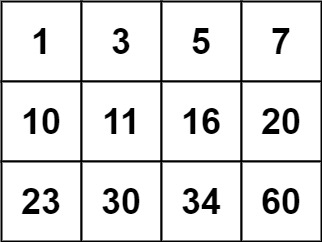
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

解法

1.暴力

解题思路

直接遍历二维数组，题目可以跑通，但是时间复杂度是O（N^2）。

cpp 复制代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for(int i = 0;i < matrix.size();i ++){
            for(int j = 0;j < matrix[0].size();j ++){
                if(target == matrix[i][j]) return true;
                if(target < martrix[i][j]) return false;    
            }
        }
        return false;
    }
};

时间复杂度O（N^2），空间复杂度O（1）

2.二分查找

解题思路：

由于这是一个有序数组，我们可以用二分查找判断 target 是否在 matrix 中。代码实现时，并不需要真的拼成一个长为 mn 的数组 a，而是将 a[i] 转换成矩阵中的行号和列号。例如示例 1，i = 9 对应的 a[i] = 30，由于矩阵有 n = 4 列，所以 a[i] 在 ⌊n / i⌋ = 2 行，在 i mod n = 1 列。

一般地，有 a[i] = matrix[⌊i / n⌋][i mod n]

cpp 复制代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(),n = matrix[0].size();
        int left = 0,right = m * n - 1;
        while(left <= right){
            int mid = (right + left) / 2;
            int x = matrix[mid / n][mid % n];
            if(target == x) return true;
            if(target < x) right = mid - 1;
            if(target > x) left = mid + 1;
        }
        return false;
    }
};

时间复杂度O（NLogN），空间复杂度O（1）