力扣108.讲有序数组转换为二叉搜索树
108. 将有序数组转换为二叉搜索树
难度:简单 | 题型:二叉树、分治、递归
一、题目理解
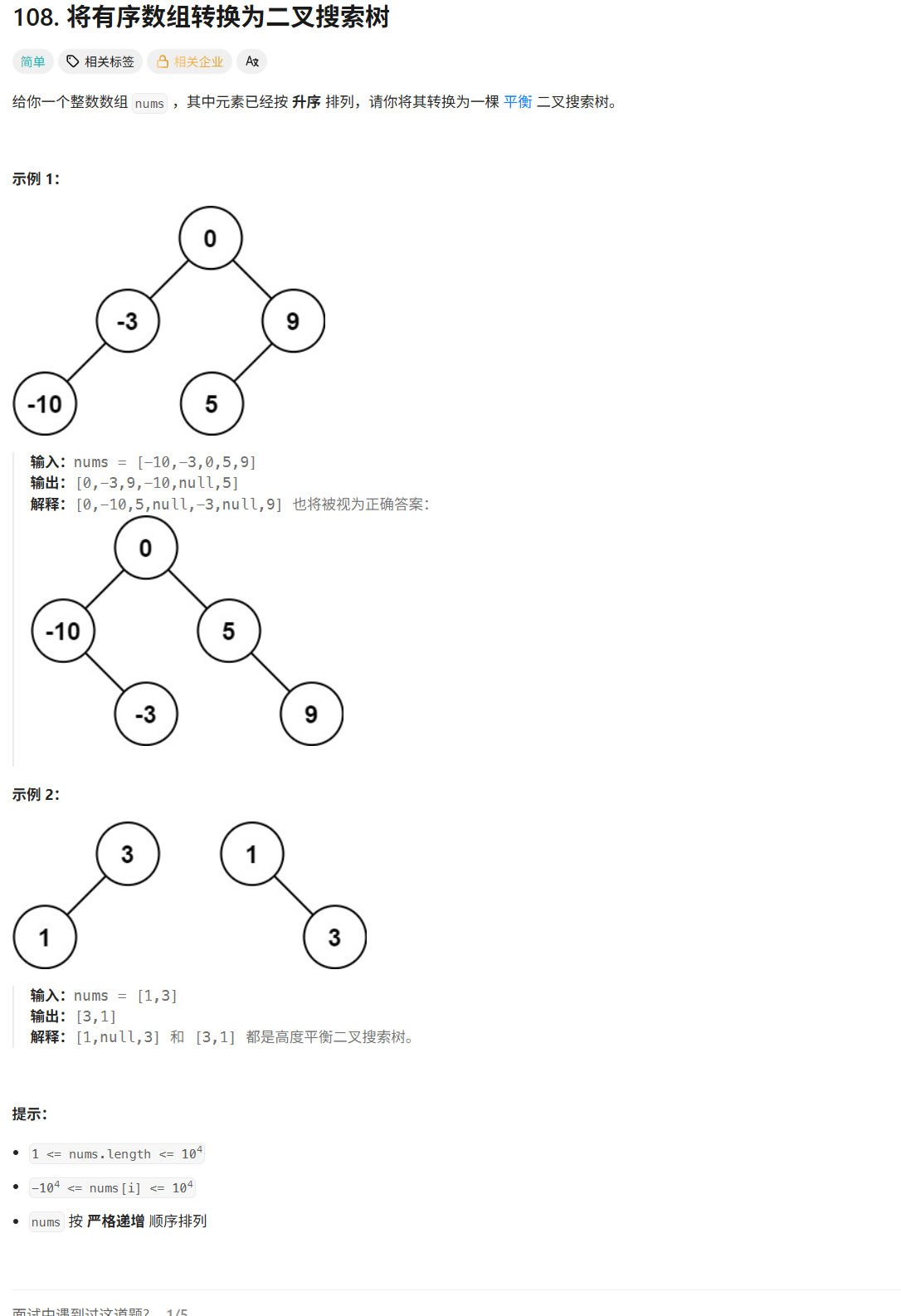
题目要求我们将一个升序数组 转换成一棵高度平衡的二叉搜索树(BST)。
平衡BST的定义:任意节点的左右子树高度差不超过1。
二叉搜索树(BST)的性质:
- 左子树所有节点的值 < 根节点的值;
- 右子树所有节点的值 > 根节点的值。
二、核心思路
数组是升序排列的,因此:
- 若我们直接取中间元素作为根节点,
- 左半部分作为左子树,
- 右半部分作为右子树,
就能保证BST的有序性 与平衡性。
这就是典型的 分治思想(Divide and Conquer)。
三、思路图示
以 nums = [-10, -3, 0, 5, 9] 为例:
nums = [-10, -3, 0, 5, 9]
中点为 0 → 根节点 = 0
左区间 [-10, -3] → 构建左子树
右区间 [5, 9] → 构建右子树
0
/ \
-3 9
/ /
-10 5这棵树既符合 BST 定义,又是平衡的。
四、代码实现(递归版 推荐写法)
java
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return build(nums, 0, nums.length - 1);
}
private TreeNode build(int[] nums, int left, int right) {
// 递归终止条件:区间为空
if (left > right) return null;
// 取中间点,防止溢出
int mid = left + (right - left) / 2;
// 构建当前节点
TreeNode root = new TreeNode(nums[mid]);
// 递归构建左右子树
root.left = build(nums, left, mid - 1);
root.right = build(nums, mid + 1, right);
return root;
}
}
五、方法二:迭代法(队列模拟递归)
虽然递归写法最简洁,但也可以通过队列模拟建树过程。
思路:
- 使用一个队列存储节点和对应区间
[left, right]。 - 取中点创建节点;
- 将左右区间加入队列;
- 持续构造直到区间耗尽。
此法更复杂但能避免递归栈溢出,适合面试时展示"多角度思维"。
六、复杂度分析
| 项目 | 递归法 | 迭代法 |
|---|---|---|
| 时间复杂度 | O(n) | O(n) |
| 空间复杂度 | O(log n)(递归栈) | O(n)(队列) |
| 平衡性 | ✅ 自动平衡 | ✅ 自动平衡 |
七、总结
| 特性 | 说明 |
|---|---|
| 数据有序 | 可以直接利用中点特性构造BST |
| 保证平衡 | 中点划分天然平衡 |
| 递归思路 | 最清晰、最常用 |
| 关键点 | mid = left + (right - left) / 2 防止溢出 |