此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第一课第三周的课程练习部分的讲解。
1.理论习题
【中英】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第三周测验
同样,这是本周理论部分的习题和相应解析,博主已经做好了翻译和解析工作,因此便不再重复。
本周理论习题较为简单,几乎所有内容都在之前的理论部分提及过,涉及代码的题也只是简单的numpy语法问题,因此就不再就某道题展开了,我们将重点放在下面的代码部分。
2.代码实操:带隐藏层的分类模型
吴恩达神经网络实战第三周同样再次粘贴整理了课程习题的博主答案,博主依旧在不借助很多现在流行框架的情况下手动构建 模型的各个部分,并手动实现传播,计算过程。
如果希望更扎实地了解原理,更推荐跟随这位博主的内容一步步手动构建模型,这样对之后框架的使用也会更得心应手。
当然,同样会在这里给出我的另一个更偏向使用现有框架和内置函数 的版本以供参考。
在第二周的代码实践部分我们用逻辑回归来训练一个猫狗图像二分类模型,但是受制于数据集,模型结构等各种因素,最终的模型测试结果并不优秀,只有58%左右的准确率。
而本周我们了解了浅层神经网络的各部分原理,知道了其如何提高拟合效果,现在便延续上一周的内容,再次在这个数据集上应用本周更新的内容,来看一看效果。
2.1 逻辑回归模型代码
先回看一下之前的模型代码:
python
class LogisticRegressionModel(nn.Module):
# 类继承自nn.Module,是 PyTorch 所有模型的基类
#初始化方法
def __init__(self):
super().__init__() #父类初始化,用于注册子模块等,涉及源码,这里当成固定即可。
self.flatten = nn.Flatten() #把张量后三维展平为一维(通道C*高H*宽W)
self.linear = nn.Linear(128 * 128 * 3, 1) # 输入是128x128x3,输出1个加权和
# nn.Linear接受的是二维输入[batch_size, features],这里是[32,128 * 128 * 3]
# 但Linear层不需要在参数里写 batch 维度,它内部会自动处理批量输入,只关心每个样本的特征数和每个样本输出的维度,这也是广播机制的应用。
self.sigmoid = nn.Sigmoid() #激活函数
#向前传播方法
def forward(self, x):
# 现在,x的维度是[32,3,128,128]
x = self.flatten(x) #1.展平
# 现在,x的维度是[32,128 * 128 * 3]
x = self.linear(x) #2.过线性组合得到加权和
# 现在,x的维度是[32,1]
x = self.sigmoid(x) #3.过激活函数得到输出
# 现在,x的维度是[32,1]
return x虽然注释较多,但其原理并不复杂,我们看向前传播函数,实际上一次正向传播只有三步显式计算。
2.2 浅层神经网络模型代码
python
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten() #
# 隐藏层:输入128*128*3维特征,输出4个神经元
self.hidden = nn.Linear(128 * 128 * 3, 4)
# 隐藏层激活函数:ReLU,作用是加入非线性特征
self.ReLU = nn.ReLU()
# 输出层:将隐藏层的 4 个输出映射为 1 个加权和
self.output = nn.Linear(4, 1)
self.sigmoid = nn.Sigmoid()
# 前向传播方法
def forward(self, x):
# 输入 x 的维度为 [32, 3, 128, 128]
x = self.flatten(x)
# 展平后 x 的维度为 [32, 128 * 128 * 3]
x = self.hidden(x)
# 通过隐藏层线性变换后,x 的维度为 [32, 4]
x = self.ReLU(x)
# 经过 ReLU 激活后形状不变,仍为 [32, 4]
x = self.output(x)
# 通过输出层得到加权和,形状变为 [32, 1]
x = self.sigmoid(x)
# 经过 sigmoid 激活后得到 0~1 的概率值,形状仍为 [32, 1]
return x这就是设置了四个隐藏层神经元的浅层神经网络的代码,可以发现,在Pytorch的内置方法帮助下,我们只不过相对逻辑回归改动了几行代码,便实现了从逻辑回归到浅层神经网络进行二分类的效果。
2.3 验证模型优化
现在,我们依旧使用上周的代码,只将模型替换为浅层神经网络而不改变其他任何部分 (完整代码附在文末)。
先来看一张测试结果:
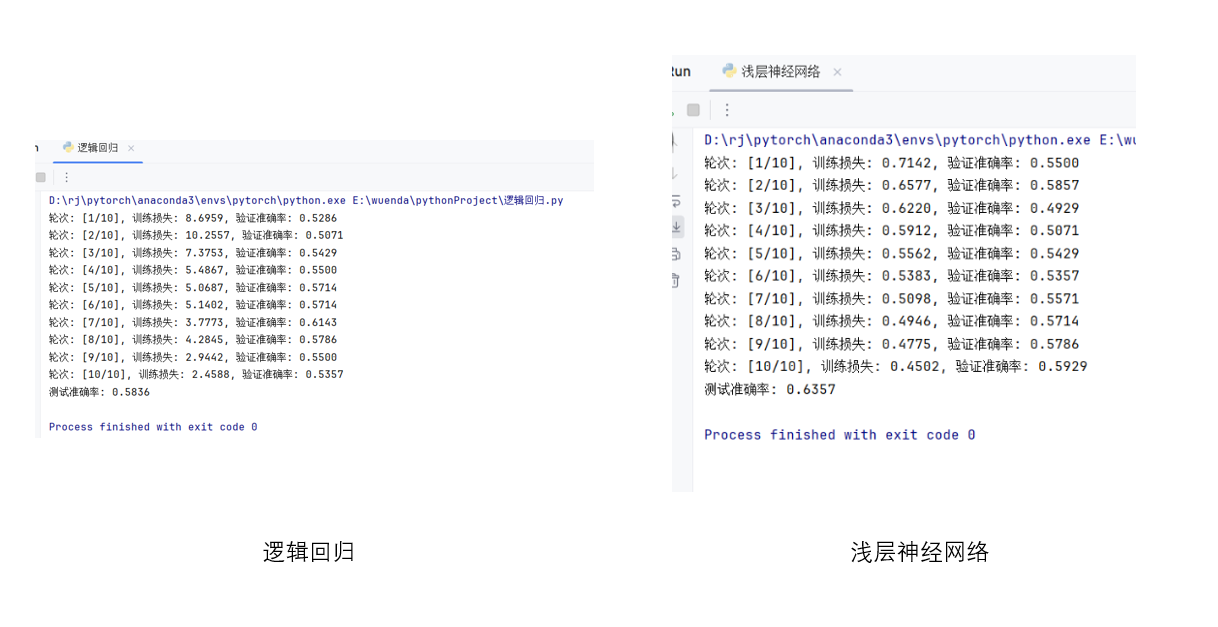
如果只看这两张图的对比,可能会想,只是简单的扩大一下网络的规模就实现了准确率的提升,确实差别展示的非常明显。
但可惜,事实并非如此,实际上,图中右侧的结果只是多次运行结果中最好的一次,几乎不可控,就像抽卡游戏里非常小概率的金卡一样。而实际上,最终测试的准确率依旧在50%到60%之间徘徊。
那问题又来了,那增加隐藏层就一点作用也没有吗?
答案当然是否定的,我们再来看一组对比:
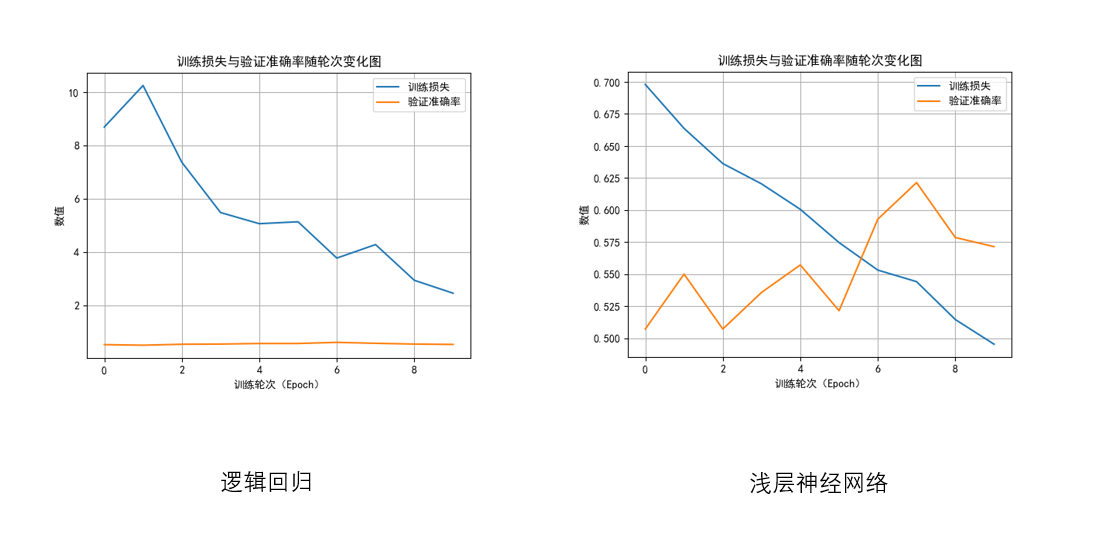
我们观察两幅图像,会很明显的发现区分。
- 在逻辑回归的图像中,准确率的曲线几乎看不出幅度,而在浅层神经网络中,它甚至已经和损失曲线相相交了。
回看刚刚每轮的损失,我们会发现,造成这种差别的原因是:准确率只在0到1间波动,而逻辑回归的平均损失却在1-10这个量级内,相比之下,浅层神经网络的平均损失已经降到了0到1之间。 - 逻辑回归的损失在数值高的情况下,相比浅层神经网络的波动也较大,而浅层神经网络的下降趋势几乎成了一条直线。
而这是因为逻辑回归因为模型太简单、只能学习线性关系,训练时更容易在高损失区震荡;而浅层神经网络具备初步非线性表达能力,能更稳定地逼近最优解,损失下降更平滑、更接近直线。
从这方面来看,增加隐藏层又有其提升。
可是还有一个问题,损失函数是用来反向传播更新参数从而提高拟合效果,提高准确率的,那现在损失变小准确率不提升是为什么 ?
在这次代码实践中,我们重点讨论一下这个问题。
2.4 为什么损失减少不增加准确率?
虽然损失函数的值在不断下降,但准确率却没有显著提高,这并不矛盾,我们来细究一下:
首先,损失函数本质上衡量的是模型输出概率与真实标签的差距 ,而准确率衡量的是最终分类结果是否正确 ,两者关注的维度不同。
当模型预测的概率逐渐接近真实标签(例如从 0.49 提高到 0.51 或从 0.4 提高到 0.6),损失会明显下降,但是只要这些概率在 0.5 的分类阈值附近徘徊,模型的预测仍可能被判定为错误,于是准确率就不会显著改变。
更进一步来说,在模型训练初期,损失的下降主要来自于"模型更有信心地接近正确答案",但这种接近往往还不足以跨过分类边界 。
例如,对于真实标签为 1 的样本,输出可能从 0.3 提升到 0.4,这的确让损失下降了很多,但它仍被判断为 0 类,这对准确率没有任何贡献。同样地,若对于真实为 0 的样本,输出从 0.8 降为 0.6,也会使损失变小,但预测依旧是错误的类别,如图所示:

还有一种情况也会导致损失在下降,但准确率"卡住不动",那就是数据本身太复杂。 我们可以把它想象成两类数据混在一起,不是泾渭分明地分成左右两堆,而是交错、环绕,甚至夹杂着噪声。浅层神经网络虽然比逻辑回归更聪明一点,但它的"想象力"依然有限,只能学会把整体误差变小,却画不出一条真正把两类数据明显分开的界线,就像这张图:
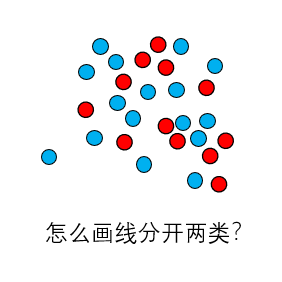
因此,在本次实操中我们会发现:损失下降说明模型确实在学习,但如果模型能力不足、特征没有被有效分离,或者分类阈值附近的样本占比过高,那么准确率依旧可能停留在50%到60%之间。
而如何进一步提升准备率,便需要我们继续学习,继续优化。
最后附上完整代码,依旧要强调的是,在规范流程里,我们应该根据每次验证的准确率调整超参数,最后再进行测试,只是这部分内容还在后面,我们经过系统学习后再正式引入这部分。
python
import torch
import torch.nn as nn
import torch.optim as optim
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, random_split
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
transform = transforms.Compose([
transforms.Resize((128, 128)),
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))
])
dataset = datasets.ImageFolder(root='./cat_dog', transform=transform)
train_size = int(0.8 * len(dataset))
val_size = int(0.1 * len(dataset))
test_size = len(dataset) - train_size - val_size
train_dataset, val_dataset, test_dataset = random_split(dataset, [train_size, val_size, test_size])
train_loader = DataLoader(train_dataset, batch_size=32, shuffle=True)
val_loader = DataLoader(val_dataset, batch_size=32, shuffle=False)
test_loader = DataLoader(test_dataset, batch_size=32, shuffle=False)
class ShallowNeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
# 隐藏层
self.hidden = nn.Linear(128 * 128 * 3, 4) # 1 个隐藏层,4 个神经元
self.ReLU = nn.ReLU()
# 输出层
self.output = nn.Linear(4, 1)
self.sigmoid = nn.Sigmoid()
def forward(self, x):
x = self.flatten(x)
x = self.hidden(x)
x = self.ReLU(x)
x = self.output(x)
x = self.sigmoid(x)
return x
model = ShallowNeuralNetwork()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = nn.BCELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
epochs =10
train_losses = []
val_accuracies = []
for epoch in range(epochs):
model.train()
epoch_train_loss = 0
for images, labels in train_loader:
images, labels = images.to(device), labels.to(device).float().unsqueeze(1)
outputs = model(images)
loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_train_loss += loss.item()
avg_train_loss = epoch_train_loss / len(train_loader)
train_losses.append(avg_train_loss)
model.eval()
val_true, val_pred = [], []
with torch.no_grad():
for images, labels in val_loader:
images = images.to(device)
outputs = model(images)
preds = (outputs.cpu().numpy() > 0.5).astype(int).flatten()
val_pred.extend(preds)
val_true.extend(labels.numpy())
val_acc = accuracy_score(val_true, val_pred)
val_accuracies.append(val_acc)
print(f"轮次: [{epoch + 1}/{epochs}], 训练损失: {avg_train_loss:.4f}, 验证准确率: {val_acc:.4f}")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(train_losses, label='训练损失')
plt.plot(val_accuracies, label='验证准确率')
plt.title("训练损失与验证准确率随轮次变化图")
plt.xlabel("训练轮次(Epoch)")
plt.ylabel("数值")
plt.legend()
plt.grid(True)
plt.show()
model.eval()
y_true, y_pred = [], []
with torch.no_grad():
for images, labels in test_loader:
images = images.to(device)
outputs = model(images)
preds = (outputs.cpu().numpy() > 0.5).astype(int).flatten()
y_pred.extend(preds)
y_true.extend(labels.numpy())
acc = accuracy_score(y_true, y_pred)
print(f"测试准确率: {acc:.4f}")