最近准备research intern面试,发现好多厂好像不考察LeetCode了,转而考察手写torch模型结构以及numpy手撕ML,赶上周末比较闲,抽空手敲一遍Minimind,快速复习一下LLM相关的基础知识,其中穿插着各种模块以及LLM训练中经常遇到的一些现象一起温习。

RMSNorm
理论部分
Norm的作用 :大部分Norm的作用都是归一化数据分布,使得tensor的均值为0,方差为1,稳定训练,防止loss spike (所有模型都面临训练不稳定,它可能发生在预训练的开始、中间或结束阶段,loss spike指的是大模型训练过程中出现的loss突然暴涨的情况),RMSNorm和QKNorm的作用基本一致。
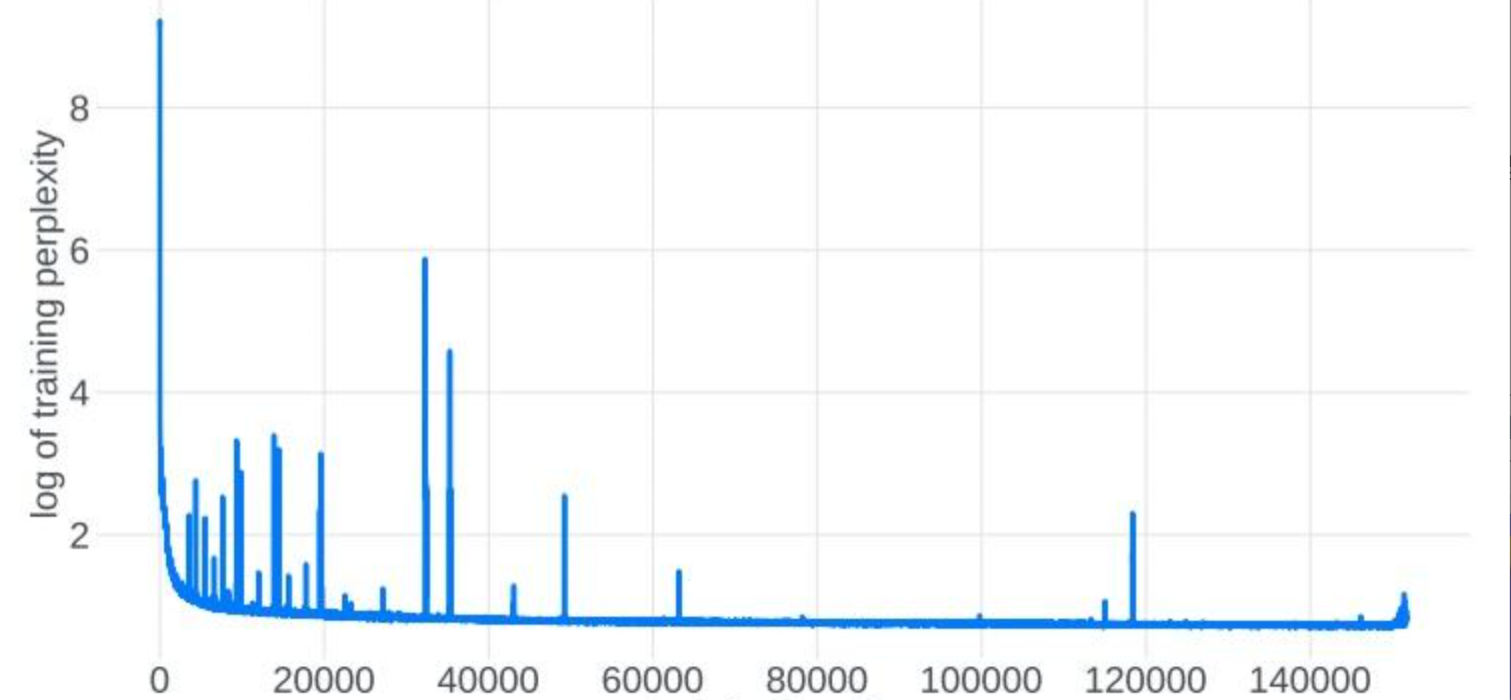
额外聊一下loss spike的原因:
- 从优化的角度理解:大模型训练一般使用Adam优化器,在训练到某个阶段,假设模型已经收敛到某个相对最优点,此时理想的参数更新趋势是保持稳定的状态,但事实并非如此 ------ 更新参数会再次汇入非稳定的状态。随机事件的叠加进入单峰的正态分布的必要条件之一是各个随机事件事件之间应该是相互独立的,但是梯度变化以及更新参数的变化并不能特别好的满足独立性这一条件,而这一点恰恰是导致更新参数振荡,loss spike出现以及loss 不收敛的重要原因之一。而梯度变化不独立的原因在于:1)浅层参数长时间不更新,2)batch_size 太大,后期梯度更新趋于平稳。
- 从数学的角度理解:以单项式Y=W*X为例,loss的梯度链式法则如下 g r a d L = d L / d W = d L / d Y × d Y / d W = d L / d Y × X grad_L=dL/dW=dL/dY \times dY/dW = dL/dY \times X gradL=dL/dW=dL/dY×dY/dW=dL/dY×X,因此
loss的梯度大小是和输入tensor X的值成正比,如果X过大或过小都容易梯度爆炸/消失,因此需要每层Norm归一化tensor,标准差为1。- 解决方案:即使加上Norm依然可能出现spike的情况,参考下面文章解决:https://zhuanlan.zhihu.com/p/10927658580
RmsNorm的好处 :llama引入RmsNorm,去掉 LayerNorm 的"平移/均值(re-centering)"项,只保留"缩放/方差(re-scaling)"项,用均方根(RMS)代替标准差,减少一次统计量计算,参数更少,效果相当甚至更好。其中 γ \gamma γ是模型可训练参数 。
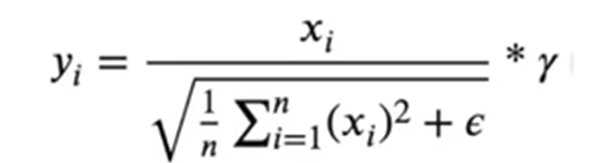
- 无 bias:没有 LayerNorm 中的可训练偏置 b 。
- 无 mean subtraction:不做 x−μ 。
- epsilon (ϵ ):防止除零,通常 1e-8~1e-6。
手撕代码
py
import torch
import torch.nn as nn
class RMSNorm(nn.Module):
def __init__(self, hidden_size, eps=1e-7):
self.hidden_size = hidden_size
self.eps = eps
self.gamma = nn.Parameter(torch.ones(hidden_size))
def _norm(self, x):
# rsqrt(x) = 1/根号下x
rms = x.pow(2).mean(-1, keepdim=True).add(self.eps).rsqrt()
return x * rms
def forward(self, hidden_state):
return self.gamma * self._norm(hidden_state) RoPE/YaRN
为什么要相对位置编码 :普通的绝对位置编码 处理动态长度,且超长序列存在天生劣势,外推能力不行,且只能在第一层Block进行加法运算。而Rope这种相对位置编码 可以无缝外推超长序列,且在每层Attention处都通过乘法运算。
RoPE原理部分
RoPE的关键在于通过 绝对位置编码(通过旋转矩阵赋予绝对角度) 来实现 相对位置编码(通过QK向量乘积获得相对角度)。
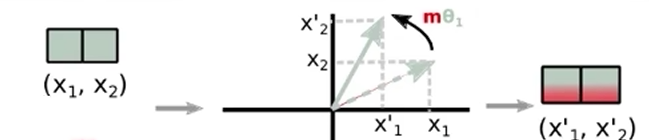
以 2维空间为例(hidden_size=2) 进行理解:
-
先用 旋转 进行 绝对位置编码 阶段(
R(m) * x) :关键在于如何表示为二维空间的旋转操作 ,对于一个二维向量x=(a,b),其shape=[1,2],将其绕原点旋转m弧度的操作,可以用矩阵乘法表示这个旋转操作R(m) * x,其中旋转矩阵R(m)如下:
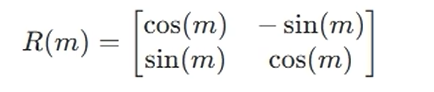
-
再基于 旋转矩阵乘法公式 的 相对位置编码 阶段(
R(n-m)) :假如attention中有2个二维向量q和k,在做矩阵乘法之前,先用对其旋转m和n弧度(用旋转进行绝对位置编码),得到 q m = R ( m ) q q_m=R(m)q qm=R(m)q , k n = R ( n ) k k_n=R(n)k kn=R(n)k,然后对其进行attention乘法, q m T k n = q T R ( m ) T R ( n ) k = q R ( n − m ) k q_m^T k_n= q^TR(m)^TR(n) k=qR(n-m)k qmTkn=qTR(m)TR(n)k=qR(n−m)k,其中R(n-m)其实就是m和n之间的相对距离。
旋转矩阵乘法公式: R ( m ) T R ( n ) = R ( − m ) R ( n ) = R ( n − m ) R(m)^T R(n) = R(-m)R(n)=R(n-m) R(m)TR(n)=R(−m)R(n)=R(n−m)
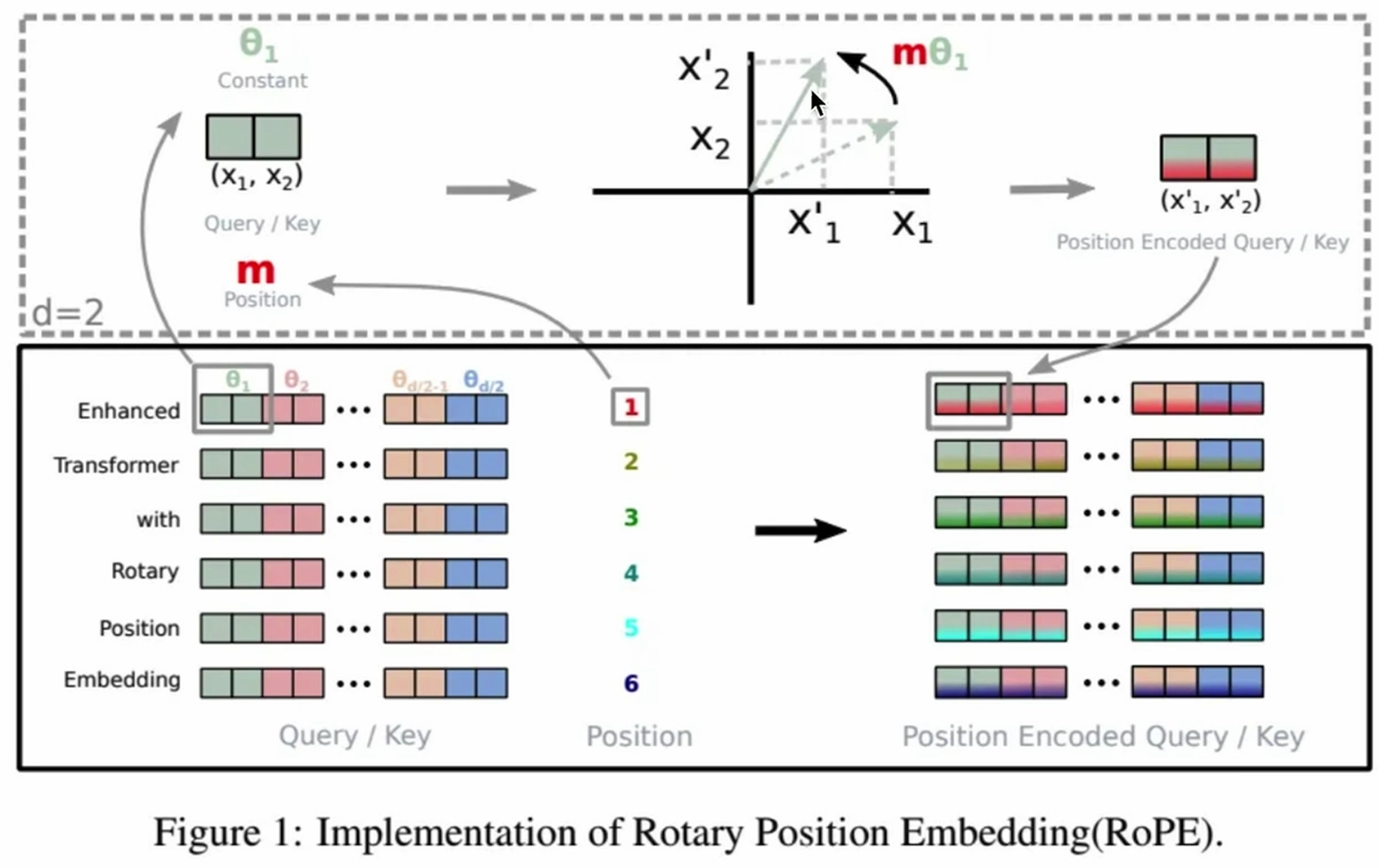
上面是以 2维空间为例(hidden_size=2) 的理解,真实代码中q和k的hidden_size通常为768/1024/2048/4096等更大的值,我们就把hidden_size拆分成多个hidden_size=2的向量,相邻两两组合,对每个二维的向量进行一个旋转 ,就可以得到下面的旋转矩阵:

- 其中的 m m m是pos_id ,表示token在seq_len维度的位置,最大值为
seq_len - 1; - 其中的 θ \theta θ是旋转弧度 ,表示hidden_size中两两一组的二维向量是第几个,最大值为
(hidden_size/2) - 1,具体来说,弧度随着维度i的增加而变化(i表示hidden_size的位置), θ i = 1 / 1000 0 2 i / d i m \theta_i=1/10000^{2i/dim} θi=1/100002i/dim; - 真正的旋转角度 是 m R ( θ i ) mR(\theta_i) mR(θi):当 i 接近 1(低维度), m R ( θ i ) mR(\theta_i) mR(θi) 的变化较大,旋转更快。当 i 接近 0(高维度), m R ( θ i ) mR(\theta_i) mR(θi) 的变化较小,旋转更慢。因此低维度具有更快的旋转(对应局部细节捕捉),高维度具有更慢的旋转(对应长距离依赖)。这种设计巧妙地结合了长距离和短距离的信息编码能力。
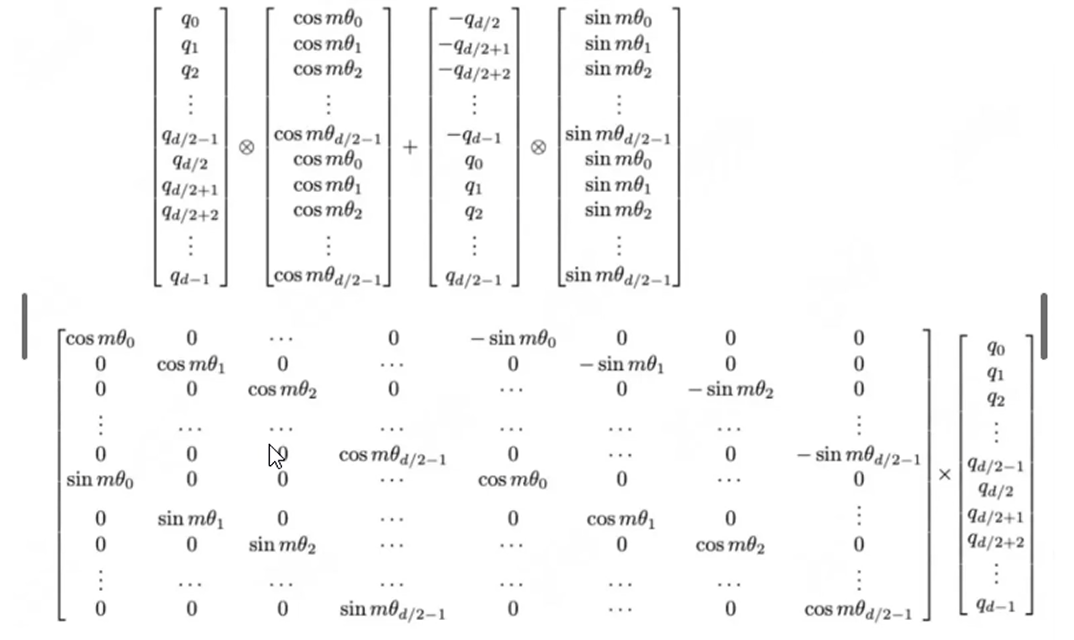
因为上面图中,旋转矩阵R(m)是非常稀疏的(很多0),计算效率不高,因此现在调整组合的方式(假如hidden_size=6):
- 之前选取相邻dim的两个小向量为一组,如hidden_size=1和hidden_size=2为一组,如下图左边。
- 现在我们选择间隔
hidden_size/2的向量为1组 ,如hidden_size=1和hidden_size=5为一组**,如下图右边。

调整hidden_size的分组方式后,旋转矩阵如下,这样就很方便代码计算了:cos抽成一列,sim抽成一列 ,分别计算即可。
YaRN原理部分
为什么有了RePE还要YaRN呢?ROPE直接外推在长文本外推中受限!
尽管ROPE在预训练窗口范围内表现优异,其主要限制在于:
- 频率不变性:在预训练时 θ i \theta_i θi被固定(RoPE的旋转角度由hidden_size决定: θ i = 1 / 1000 0 2 i / d i m \theta_i=1/10000^{2i/dim} θi=1/100002i/dim),无法适应更长的上下文长度。
- 频率分布的刚性:所有维度的频率分布固定,不支持动态调整,导致当序列长度超出预训练范围时,旋转编码出现混乱。
当上下文窗口从预训练的 L 扩展到 L' 时,相对位置 m-n 的值可能远超预期范围。此时,旋转频率无法捕捉新的位置信息,导致模型性能显著下降。
YaRN对低频使用普通放缩,对高频使用复杂放缩。具体看:https://zhuanlan.zhihu.com/p/15311461897

手撕代码
版本1:
py
# 计算基本的旋转频角度R(mθ)
def precompute_freqs_cis(hidden_size=128, max_seq_len=4096,
rope_base=10000.0, rope_scaling=None):
# 计算token间隔 hidden_size/2 两两分组以后,每组元素对应的旋转角度
# torch.arange(0, hidden_size, 2) [0, 2, 4, 6, 8, 10,..., 124, 126] 共64个
# torch.arange(0, hidden_size, 2)[: (hidden_size // 2)] 保证是hidden_size/2个
# torch.Size([128])
# theta = 1.0 / 10000^{2i/hidden_size}
freqs = 1.0 / (rope_base ** (torch.arange(0, hidden_size, 2)[: (hidden_size // 2)].float() // hidden_size))
# 生成pos_id: t = [0,....,max_seq_len] torch.Size([4096])
t = torch.arange(max_seq_len, device=freqs.device) # type: ignore
freqs_cos = torch.cos(freqs).repeat_interleave(2, dim=-1) # [seq_len, dim]
freqs_sin = torch.sin(freqs).repeat_interleave(2, dim=-1) # [seq_len, dim]
return freqs_cos, freqs_sin
# 对q和k进行旋转
def apply_rotary_emb(
xq, xk, # [batch, seqlen, num_heads, head_dim]
freqs_cos, freqs_sin, # [seq_len, dim]
pos_ids=None, unsqueeze_dim=1
):
def rotate_half(x):
# 相邻2维一组
x1, x2 = x[..., ::2], x[..., 1::2] # 间隔一半一组, 而不是相邻2个为一组
return torch.stack([-x2, x1], dim=-1).flatten(-2)
q_embed = (xq * freqs_cos.unsqueeze(unsqueeze_dim)) + (rotate_half(xq) * freqs_sin.unsqueeze(unsqueeze_dim))
k_embed = (xk * freqs_cos.unsqueeze(unsqueeze_dim)) + (rotate_half(xk) * freqs_sin.unsqueeze(unsqueeze_dim))
return q_embed, k_embed版本2:
py
基本的旋转频角度R(mθ)
def precompute_freqs_cis(hidden_size=128, max_seq_len=4096,
rope_base=10000.0, rope_scaling=None):
# 计算token间隔 hidden_size/2 两两分组以后,每组元素对应的旋转角度
# torch.arange(0, hidden_size, 2) [0, 2, 4, 6, 8, 10,..., 124, 126] 共64个
# torch.arange(0, hidden_size, 2)[: (hidden_size // 2)] 保证是hidden_size/2个
# torch.Size([128])
# theta = 1.0 / 10000^{2i/hidden_size}
freqs = 1.0 / (rope_base ** (torch.arange(0, hidden_size, 2)[: (hidden_size // 2)].float() // hidden_size))
# 生成pos_id: t = [0,....,max_seq_len] torch.Size([4096])
t = torch.arange(max_seq_len, device=freqs.device) # type: ignore
# 生成频率矩阵: t为列向量, freqs为行向量, 做外积, freqs.shape = (t.len(),freqs.len()) #shape (end,dim//2)
freqs = torch.outer(t, freqs).float() # torch.Size([4096, 128])
# 生成复数, torch.polar(abs,angle) = abs*cos(angle) + abs*sin(angle)*j
freqs_cis = torch.polar(torch.ones_like(freqs), freqs) # complex64
# freqs_cis的维度为(4096,128),相当于半径为1,角度为freqs的极坐标的复数表示
return freqs_cis
# 对q和k进行旋转
def apply_rotary_emb(
xq: torch.Tensor, # [2, seqlen, 32, 128]
xk: torch.Tensor, # [2, seqlen, 32, 128]
freqs_cis: torch.Tensor, # [seqlen,64]
):
# xq.shape = [bsz, seqlen, self.n_local_heads, self.head_dim]->[2, 1024, 32, 128]
# xq_.shape = [bsz, seqlen, self.n_local_heads, self.head_dim//2]->torch.Size([2, 1024, 32, 64])
# torch.view_as_complex用于将二维向量转换为复数域 torch.view_as_complex即([x,y]) -> (x+yj)
# 所以经过view_as_complex变换后xq_.shape = [bsz, seqlen, self.n_local_heads, self.head_dim//2]
# (bsz,1024,32,128)->(bsz,1024,32,64)
xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2))
xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2))
# freqs_cis ->(4096,64)
# freqs_cis = self.freqs_cis[start_pos : start_pos + seqlen]->(1024,64)
freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
# freqs_cis.shape = (1,x.shape[1],1,x.shape[-1]) = (1,1024,1,64)
# xq_ 与freqs_cis广播哈达玛积
# [bsz, seqlen, self.n_local_heads, self.head_dim//2] * [1,seqlen,1,self.head_dim//2]
# torch.view_as_real用于将复数再转换回实数向量, 再经过flatten展平第4个维度
# [bsz, seqlen, self.n_local_heads, self.head_dim//2] ->[bsz, seqlen, self.n_local_heads, self.head_dim//2,2 ] ->[bsz, seqlen, self.n_local_heads, self.head_dim]
xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3)
xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3)
return xq_out.type_as(xq), xk_out.type_as(xk) # [2, seqlen, 32, 128], [2, seqlen, 32, 128]
def reshape_for_broadcast(freqs_cis: torch.Tensor, x: torch.Tensor):
# ndim为x的维度数 ,此时应该为4
# freqs_cis.shape = [1024, 64]
# x.shape = [2, 1024, 32, 64]
ndim = x.ndim
assert 0 <= 1 < ndim
assert freqs_cis.shape == (x.shape[1], x.shape[-1])
shape = [d for i, d in enumerate(x.shape) if i == 1 or i == ndim - 1 else 1]
# (1,x.shape[1],1,x.shape[-1]) = (1,1024,1,64)
return freqs_cis.view(*shape)