上一篇说还有两道例题这里给大家补上
一. 栈的部分补充例题
1.逆波兰表达式
1.1 题目描述:
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
1.2 题解:
遍历字符,判断是否是数字字符,将其转为数字(Inter.parseInt())如果是运算符就弹出栈的两个元素进行运算
1.3 代码实现:
java
public int evalRPN(String[] tokens) {
//定义一个栈
Stack<Integer> stack = new Stack<>();
//1.遍历
for (int i = 0; i < tokens.length; i++) {
String str = tokens[i];
//如果是数字,就入栈
if(isInteger(str)) {
//要将字符转换为数字
stack.push(Integer.parseInt(str));
}else {
int num1 = stack.pop();
int num2 = stack.pop();
//分字符运算
switch (str) {
case "+" :
stack.push(num2 + num1);
break;
case "-":
stack.push(num2 - num1);
break;
case "*":
stack.push(num2 * num1);
break;
case "/":
stack.push(num2 / num1);
break;
}
}
}
return stack.peek();
}
public static boolean isInteger(String str) {
//判断字符是否是运算符
if(str.equals("+") ||str.equals("*")
||str.equals("-") ||str.equals("/")) {
return false;
}
return true;
}1.4(拓展知识点)后缀表达式
后缀表达式(逆波兰式)是一种计算机高效处理的表达式形式,其运算符位于操作数之后,无需括号和优先级判断。以下是关键要点:
1. 基本概念
-
定义:形如
a b c - d * +,等价于中缀表达式a + ((b - c) * d)。 -
特点:
-
运算符顺序决定计算顺序,无需括号。
-
适合栈结构计算,时间复杂度为O(n)。
-
2. 转换规则(中缀→后缀)
-
操作数:直接输出。
-
运算符:与栈顶比较优先级,高则压栈,低则弹出1。
-
括号:
(直接压栈)弹出至(。
示例:a + (b - c) * d → a b c - d * +。
3. 后缀表达式求值
-
步骤:
-
初始化栈,扫描表达式。
-
遇到操作数压栈,遇到运算符则弹出两操作数运算,结果压栈。
-
最终栈顶为结果。
-
4.中缀表达式转后缀表达式:1.每个运算都加上括号,2.把对应运算符移到括号外面,3.把括号去掉
2 .最小栈问题:
2.1 题目描述:
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
2.2 题解:(借助两个栈)
**入栈:**1)每次存放元素时,都要和最小栈的栈顶元素进行比较(<=)
2)如果最小栈第一次存放的时候是空的,那么直接存储
**出栈:**1)每次出栈时,都要判断最小栈的栈顶元素,如果相同,最小栈也得出栈
2.3 代码实现:
java
Stack<Integer> stack;
Stack<Integer> minStack;
public MinStack() {
//2.初始化栈
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int val) {
//1.入栈
stack.push(val);
//2.如果最小栈为空,就直接入栈
if(minStack.empty()) {
minStack.push(val);
}else {
//如果stack的栈顶值比最小栈的栈顶元素值小就入栈
if(stack.peek() <= minStack.peek()) {
minStack.push(stack.peek());
}
}
}
public void pop() {
//判空
if(stack.empty()) {
return;
}
int val = stack.pop();
//如果刚好出到和最小栈栈顶元素相同的值,最小栈也要出栈
if(minStack.peek() == val) {
minStack.pop();
}
}
//相当于peek()
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}其实这题不难,可以去试试。
接下来我们进入队列的学习
二. 队列(Queue)
1.介绍:
Java中的队列(Queue)是一种遵循先进先出(FIFO)原则的线性数据结构,常用于任务调度、消息传递等场景。以下是核心要点:
2.基本概念与操作
-
**FIFO原则:**元素从队尾(rear)插入,从队头(front)移除,确保最早入队的元素最先被处理。
-
核心操作:
-
enqueue(入队):添加元素到队尾,如offer(E e)或add(E e)。 -
dequeue(出队):移除并返回队头元素,如poll()或remove()。 -
peek():查看队头元素但不移除
-
-
**常用的方法:**插入:offer() / add();删除:poll() / remove();查看队头元素:peek() / element()
-
add/offer和poll/remove的区别(扩展知识)
在Java的Queue接口中,add/offer和poll/remove是两组功能相似但行为不同的方法,主要区别体现在异常处理和返回值策略上:
add()与offer()的区别
-
异常处理
add()在队列满时会抛出IllegalStateException,而offer()会返回false。这种设计使得offer()更适合容量受限的队列场景,避免程序因异常中断。 -
语义差异
add()继承自Collection接口,强调集合操作的通用性;offer()是Queue专有方法,更符合队列插入的特定语义。 -
使用建议
推荐优先使用offer(),因其通过返回值而非异常处理失败情况,代码健壮性更强。
poll()与remove()的区别
-
空队列行为
remove()在队列为空时抛出NoSuchElementException,而poll()返回null,后者更适用于需要静默处理的场景。 -
方法来源
remove()来自Collection接口,poll()是Queue的专属方法,专为队列的头部操作设计。 -
应用选择
若需明确感知空队列状态(如关键业务流程),使用remove();若允许静默失败(如任务调度),选择poll()。
这两组方法体现了Queue接口"双策略"设计:一组通过异常反馈问题(add/remove),另一组通过返回值处理(offer/poll),开发者可根据具体容错需求选择
3.核心方法的实现:
我这里是自己用双向链表来实现队列,用其他也可以,自己实现一遍可以增加对这个方法的理解。这里根据队列的性质,我们可以知道,入队是尾插,出队是头删,按这个逻辑很容易实现,要记得判空就行。
java
public class MyQueue {
static class ListNode {
public int val;
public ListNode prev;
public ListNode next;
public ListNode(int val) {
this.val = val;
}
}
//头和尾
public ListNode first;
public ListNode last;
//1.入队(先进先出)尾插法:
public void offer(int val) {
ListNode node = new ListNode(val);
//判空
if(first == null) {
first = node;
last = node;
}
//尾插
last.next = node;
node.prev = last;
last = node;
}
//2.出队(先出)头删
public int poll() {
//判空
if(first == null) {
//定义异常
throw new EmptyException("队列为空!!");
}
int val = first.val;
//只有一个结点
if(first == last) {
first = null;
last = null;
}else {
first = first.next;
first.prev = null;
}
return val;
}
//peek()
public int peek() {
if (first == null) {
throw new EmptyException("队列为空!!");
}
return first.val;
}
//3.size()
public int size() {
ListNode cur = first;
int count = 0;
while(cur != null) {
count++;
cur = cur.next;
}
return count;
}
//empty
public boolean empty() {
return first == null;
}
}3.循环队列(特殊点和难点)
3.1 基本介绍
Java中的循环队列是一种通过数组实现的队列结构,通过模运算实现存储空间的首尾循环利用,解决了顺序队列的"假溢出"问题。其核心特性是通过front和rear指针的环形移动实现高效的元素存取,并通过保留一个空位或size属性来区分队空和队满状态。如下图:
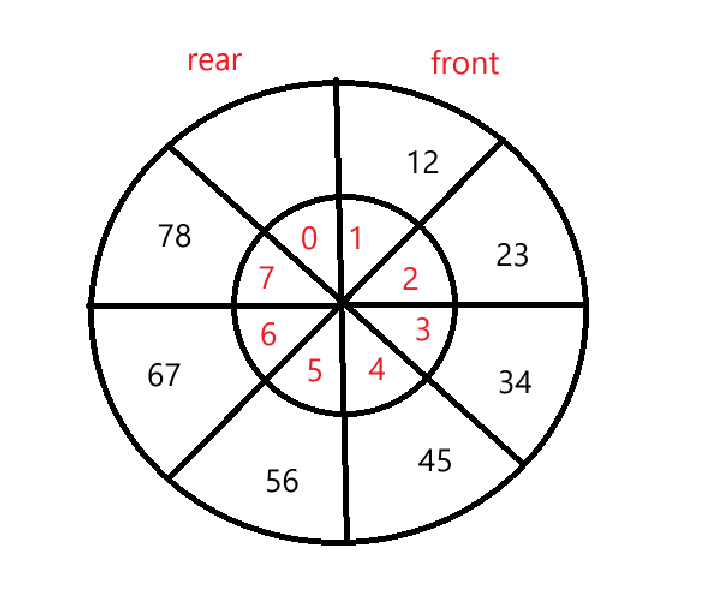
3.2 核心实现要点
-
指针计算
入队时rear指针通过
(rear + 1) % capacity移动,出队时front指针同理,确保指针到达数组末尾后回到起始位置。这种设计使得数组空间利用率达到100%。 -
状态判断
-
队空条件:
front == rear -
队满条件:
(rear + 1) % capacity == front(保留一个空位方案)或通过size属性记录元素数量。
-
-
动态扩容
当队列满时需扩容,通常将数组长度翻倍并重新排列元素(front到rear之间的连续段)
3.3 上手实践(用数组实现循环队列)
在循环队列中,我们主要要解决两个疑问:
1) rear 从 7 下标到 0 下标的操作,可以通过取模运算实现指针的循环移动。当rear指针到达数组末尾时(如下标7),执行rear = (rear + 1) % capacity即可使其回到0下标。
**2)**我们判断队列是满还是空的依据
-
队列空的条件:
front == rear,表示无有效元素。 -
队列满的条件:牺牲一个存储单元,通过
(rear + 1) % capacity == front判断。此时rear指针的下一个位置是front,说明空间已满。

代码演示:
java
public class CircularQueue {
//定义一个数组
public int[] array;
public int front;
public int rear;
//构造方法
public CircularQueue(int k) {
array = new int[k+1];
}
public boolean isFull() {
return (rear + 1) % array.length == front;
}
//入队
public boolean enQueue(int value) {
//1.判满
if (isFull()) {
return false;
}
array[rear] = value;
rear = (rear + 1) % array.length;
return true;
}
//判空
public boolean isEmpty() {
return rear == front;
}
public boolean deQueue() {
//判空
if (isEmpty()) {
return false;
}
front = (front + 1) % array.length;
return true;
}
public int Front() {
if (isEmpty()) {
return -1;
}
return array[front];
}
public int Rear() {
if (isEmpty()) {
return -1;
}
int index = -1;
if(rear == 0) {
index = array.length-1;
}else {
index = rear-1;
}
return array[index];
//(rear - 1 + capacity) % capacity
}
}双端队列的介绍和几个例题就留下次讲啦~