数据结构初阶：时间和空间复杂度

1. 算法效率

算法效率分析包含两种：时间复杂度分析 和空间复杂度分析。 时间复杂度主要衡量的是一个算法的运行速度，而空间复杂度主要衡量一个算法所需要的额外空间。

以前计算机存储容量很小，人们就很在乎空间效率（空间复杂度），但现在计算机的存储容量已经比较大，人们就更在乎时间效率（时间复杂度）。

2. 时间复杂度

2.1 时间复杂度的概念

算法的时间复杂度，并不是计算代码上机测试所花的时间，而是计算语句的执行次数。
一个算法所花费的时间与其中语句的执行次数成正比例，算法中的基本操作的执行次数，为算法的时间复杂度。

循环的时间复杂度：

2.2 大O的渐进表示法

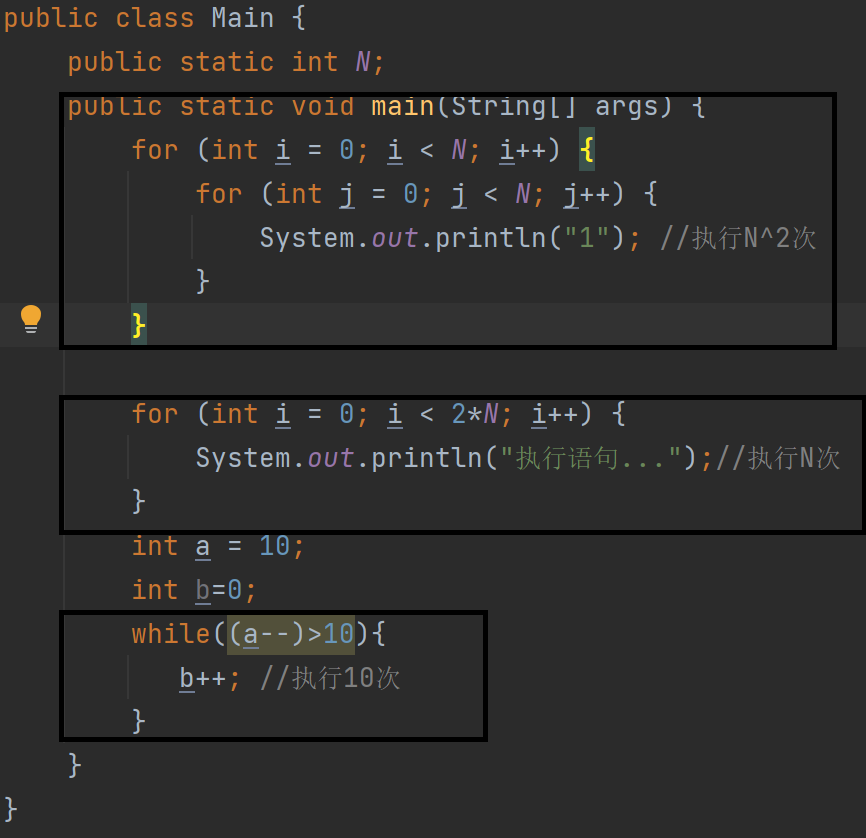
main执行的基本操作次数：F(N) = N^2+2*N+10（不是时间复杂度）

（有人就会有疑问最后加的不应该是12吗（定义变量的两条语句难道不算了吗？）因为大O的渐进表示法只是用来计算大概的语句执行次数。用这个方法计算出式子后，离得到时间复杂度就只差最后一步！！（推导大O阶）
2.3 推导大O阶方法
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中，只保留最高阶项。
3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。
推导大O阶以后得到时间复杂度，main的时间复杂度为：O(N^2)
**解读：**F(N) = N^2+2*N+10------>N^2+2*N+1----->N^2（最高阶项数系数已经为1了）
通过上面我们发现，计算时间复杂度忽略了对结果影响不大的项，简洁明了的表达了执行次数。
另外我们可以想到有些算法存在时间复杂度最好、最坏和平均的情况。++（一般所说的时间复杂度和空间复杂度都是指最坏情况下）（比如两个方法都可以解决同一个问题，那么比较时间复杂度就能判定哪个方法的执行效率高）++

递归的时间复杂度：

递归的时间复杂度= 递归的次数*每次递归执行的语句次数；

一：先用大O的渐近表示法计算

二：推导大O阶（就得到时间复杂度）

例：

复制代码

public static void func(int n){
    if(n==0) return ;
    n--;
    func(n);
}

第一次递归执行一条语句；

第二次递归执行一条语句；

......

第n次递归执行一条语句；

当第n+1次递归执行return；

最后F(n)=n; 因此时间复杂度就为O(n) 。

3.空间复杂度

空间复杂度是计算程序运行时，临时内存占用存储空间大小的量度。 空间复杂度并不是计算程序占用了多少bytes的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。

空间复杂度的计算和时间复杂度差不多。

例1：循环的空间复杂度

猜猜func1的空间复杂度是什么？

java 复制代码

//计算func1的空间复杂度
public void func1(int[] arr){
    for (int i = 0; i < arr.length-1; i++) {
        Boolean is = false;
        for (int j=0;j< arr.length-i-1;j++){
            if (arr[j]>arr[j+1]){
                int tmp = arr[j];
                arr[j]=arr[j+1];
                arr[j+1]=tmp;
                is=true;
            }
        }
        if (is==false){
            break;
        }
    }
}

答案：func1()方法只创建了常数个（一个）临时变量------》**is；**所以空间复杂度为O(1);

func1的形参可不算入空间复杂度，因为那是必须需要的空间！！！

例2：计算fibonacci()函数的空间复杂度

java 复制代码

//fibonacci()是在计算斐波那契的第n项
    //这里默认n>=1
    public int fibonacci(int n){
        int[] fibarr = new int[n+1];
        fibarr[0]=1;
        fibarr[1]=1;
        for (int i = 2; i < n; i++) {
            fibarr[i]= fibarr[i-1]+fibarr[i-2];
        }
        return fibarr[n-1];
    }

答案：开辟了n个空间，所以空间复杂度为O(n)

例3：递归的空间复杂度

java 复制代码

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {
return N < 2 ? N : factorial(N-1)*N;
}

解读：将进行n次递归（进入函数开始第一次递归），每次递归都会开辟一个栈帧（一块空间）。

答案：实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)