【C++数据结构进阶】吃透 LRU Cache缓存算法：O (1) 效率缓存设计全解析

前言

在程序员的技术成长路上，缓存是绕不开的核心话题 ------ 小到浏览器的本地存储，大到分布式系统的 Redis 集群，缓存的存在总能让数据访问速度实现质的飞跃。而在众多缓存替换算法中，LRU（Least Recently Used）绝对是 "明星选手"：它原理直观、实现高效，被广泛应用于操作系统、数据库、框架源码等各类场景。

如果你曾被 "如何设计一个 O (1) 时间复杂度的 LRU 缓存" 面试题难住，或是想深入理解 LRU 的底层逻辑，这篇文章将带你从 0 到 1 吃透 LRU Cache。下面就让我们正式开始吧！

一、缓存与 LRU：为什么 LRU 能成为主流？

在正式讲解 LRU 之前，我们得先搞懂两个核心问题：什么是缓存？为什么 LRU 算法能脱颖而出？

1.1 缓存的本质：速度鸿沟的 "桥梁"

缓存（Cache）本质上是一种高速数据存储层，位于速度相差较大的两种硬件或系统之间，用于协调数据传输的速度差异。就像生活中常用的物品会放在桌面（高速缓存），不常用的会放进柜子（低速存储），缓存的核心思想是 "把最常用的数据放在最快的地方"。

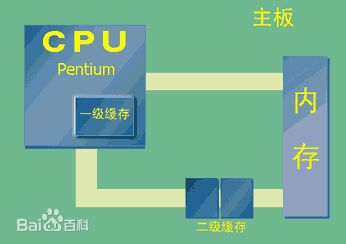
从狭义到广义，缓存无处不在：

CPU 缓存：位于 CPU 和主存之间，用高速 SRAM 芯片实现，速度是主存的数十倍，解决 CPU 运算速度与主存读取速度不匹配的问题；

内存缓存：位于内存和硬盘之间，比如操作系统的页面缓存，让频繁访问的硬盘数据常驻内存，避免重复的磁盘 IO；

应用层缓存：比如浏览器的 Internet 临时文件夹、Redis 数据库，甚至是我们自己写的本地缓存，都是为了减少对后端服务或底层存储的访问压力。

但缓存的容量始终是有限的 ------CPU 一级缓存可能只有几十 KB，Redis 实例的内存也有上限。当新数据需要存入，而缓存已经满了的时候，就必须 "踢掉" 一部分旧数据，这就是缓存替换策略要解决的问题。

1.2 主流缓存替换算法对比：LRU 的优势在哪？

常见的缓存替换算法有四种，我们用一个简单的例子对比它们的逻辑：假设缓存容量为 3，数据访问顺序是 1→2→3→4→2→5，看看每种算法会保留哪些数据：

算法	核心逻辑	最终缓存数据	优缺点
FIFO（先进先出）	按数据存入顺序淘汰最早的	3、4、5	实现简单，但忽略数据访问频率，可能淘汰常用数据
LFU（最近最不常使用）	淘汰访问次数最少的数据	2、4 、5	考虑访问频率，但需要统计次数，实现复杂，且不适合突发访问场景
OPT（最优替换）	淘汰未来最久不会使用的数据	2、4、5	理论最优，但需要预知未来访问，实际无法实现
LRU（最近最少使用）	淘汰最长时间未被使用的数据	2、4、5	兼顾直观性和高效性，无需统计次数，仅关注最近访问时间

可以看到，LRU 是性价比最高的选择：它的逻辑符合人类使用习惯（最近使用的 data 未来大概率还会被使用），且实现难度低、时间复杂度可控，完美平衡了 "效果" 和 "成本"，这也是它成为工业界首选的核心原因。

1.3 LRU 的核心定义："最久未使用" 才是关键

很多人会把 LRU 翻译成 "最近最少使用"，但更形象的理解是 "最久未使用"------ 算法的核心规则是：

当缓存未满时，新数据直接存入；

当缓存已满时，淘汰 "距离上次使用时间最久" 的数据；

当访问（get）或更新（put）缓存中的数据时，该数据会被标记为 "最近使用"，优先级提升。

举个生活中的例子：你的手机桌面只能放 3 个 APP，你先装了微信、抖音、淘宝（缓存：[微信，抖音，淘宝]）；之后你打开了微信（访问操作），微信变成最近使用，缓存调整为 [抖音，淘宝，微信]；接着你装了小红书（缓存满了），此时最久未使用的是抖音，所以抖音被淘汰，缓存变为 [淘宝，微信，小红书]------ 这就是 LRU 的核心逻辑。

二、LRU 的实现思路：如何做到 O (1) 效率？

要实现 LRU，关键是解决两个核心问题：

如何快速找到 "最久未使用" 的数据（以便淘汰）？

如何快速插入新数据、更新已有数据的优先级？

如果用常规数据结构实现，会遇到明显的效率瓶颈：

数组：插入 / 删除需要移动元素，时间复杂度 O (n)；

单链表：查找数据需要遍历，时间复杂度 O (n)；

哈希表：查找 / 插入 O (1)，但无法记录数据的访问顺序，无法快速找到 "最久未使用" 的数据。

2.1 核心数据结构：双向链表 + 哈希表

要实现 O (1) 时间复杂度的 get 和 put 操作，必须结合两种数据结构的优势，形成 "互补"：

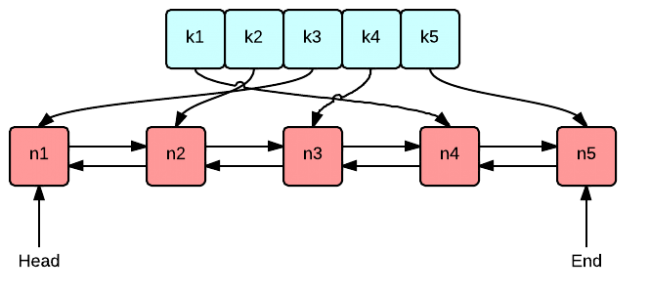
双向链表（std::list） ：负责维护数据的访问顺序 ，最近使用的数据放在链表头部，最久未使用的放在链表尾部。双向链表的优势是支持 O (1) 时间的任意位置插入和删除（只需修改前后节点的指针）；

哈希表（std::unordered_map） ：负责快速查找数据，key 是缓存的键值，value 是双向链表中对应节点的迭代器（iterator）。哈希表的优势是查找、插入、删除的时间复杂度均为 O (1)。

这个组合的 "精妙之处" 在于：哈希表的 value 存储链表迭代器，使得我们可以通过 key 快速定位到链表中的节点，再通过双向链表的 O (1) 插入 / 删除操作调整节点顺序，最终实现所有操作的 O (1) 效率。

2.2 数据结构设计细节

我们先明确 C++ 中具体的数据结构选型：

双向链表 ：使用std::list<std::pair<int, int>>，每个节点存储**(key, value)**键值对 ------ 因为淘汰链表尾部节点时，需要通过 key 删除哈希表中对应的记录；

哈希表 ：使用std::unordered_map<int, std::list<std::pair<int, int>>::iterator>，key 是缓存的 key，value 是链表节点的迭代器 ------ 通过迭代器可以直接操作链表节点，无需遍历链表；

缓存容量 ：使用size_t _capacity记录缓存的最大容量，当链表大小超过容量时，触发淘汰逻辑。

2.3 LRU 核心操作流程拆解

LRU 的核心操作有两个：get（获取数据）和 put（插入 / 更新数据），我们逐一拆解它们的执行流程。

2.3.1 get 操作：获取数据并更新优先级

get 操作的目标是：根据 key 查找缓存，如果存在则返回 value，并将该节点移动到链表头部（标记为最近使用）；如果不存在则返回 - 1。

具体步骤：

用哈希表查找 key 对应的迭代器：auto hash_it = _hash_map.find(key)；

如果哈希表中没有该 key（hash_it == _hash_map.end()），返回 - 1；

如果存在，通过迭代器获取链表节点的键值对*std::pair<int, int> kv = hash_it->second；

从链表中删除该节点（_list.erase(hash_it->second)）------ 双向链表删除已知迭代器的节点是 O (1)；

将该节点插入到链表头部（_list.push_front(kv)）------ 标记为最近使用；

更新哈希表中该 key 对应的迭代器（_hash_map[key] = _list.begin()）------ 因为节点位置变了，迭代器需要重新指向头部；

返回 kv.second（即 value）。

2.3.2 put 操作：插入或更新数据

put 操作的目标是：如果 key 已存在，则更新 value 并将节点移到头部；如果 key 不存在，则插入新节点到头部，若缓存已满则淘汰链表尾部节点。

具体步骤：

用哈希表查找 key 对应的迭代器：auto hash_it = _hash_map.find(key)；

如果 key 已存在（hash_it != _hash_map.end()）：① 通过迭代器获取链表节点std::pair<int, int> kv = hash_it->second；② 更新节点的 value（kv.second = value）；③ 从链表中删除该节点（_list.erase(hash_it->second)）；④ 将更新后的节点插入到链表头部（_list.push_front(kv)）；⑤ 更新哈希表中的迭代器（_hash_map[key] = _list.begin()*）；

如果 key 不存在（hash_it == _hash_map.end()）：① 检查缓存是否已满（_list.size() >= _capacity）：a. 如果已满，获取链表尾部节点的 key（int delete_key = _list.back().first）；b. 删除链表尾部节点（_list.pop_back()）------ 淘汰最久未使用的数据；c. 删除哈希表中该 key 对应的记录（_hash_map.erase(delete_key)）；② 创建新的键值对节点，插入到链表头部（_list.push_front(std::make_pair(key, value))）；③ 在哈希表中添加该 key 与链表头部迭代器的映射（_hash_map[key] = _list.begin()）。

2.4 为什么必须用双向链表？

可能有同学会问：为什么不用单链表？这里的关键是 "删除节点时需要前驱节点的指针"。

在单链表中，要删除一个节点，必须先找到它的前驱节点，这需要遍历链表（O (n) 时间）；而双向链表的每个节点都有 prev 和 next 指针，通过迭代器可以直接获取前后节点的信息，删除操作只需修改两个指针，无需遍历，实现 O (1) 时间复杂度。

这也是双向链表在 LRU 实现中不可替代的原因 ------ 它让节点的删除操作摆脱了对 "遍历查找前驱" 的依赖，完美配合哈希表实现高效操作。

三、C++ 完整实现：手把手写 LRU Cache

基于上面的思路，我们来编写完整的 C++ 实现代码。代码将基于 LeetCode 第 146 题《LRU 缓存》的接口规范编写，大家可以直接提交进行验证。

3.1 完整代码实现

cpp 复制代码

#include <iostream>
#include <list>
#include <unordered_map>
#include <utility> // for std::make_pair

using namespace std;

class LRUCache {
public:
    // 构造函数：初始化缓存容量
    LRUCache(int capacity) {
        _capacity = capacity;
    }

    // 获取key对应的value，不存在返回-1
    int get(int key) {
        // 1. 在哈希表中查找key
        auto hash_it = _hash_map.find(key);
        // 2. 未找到，返回-1
        if (hash_it == _hash_map.end()) {
            return -1;
        }
        // 3. 找到，获取链表节点的迭代器
        auto list_it = hash_it->second;
        // 4. 取出节点的键值对
        pair<int, int> kv = *list_it;
        // 5. 从链表中删除该节点
        _list.erase(list_it);
        // 6. 将节点插入到链表头部（标记为最近使用）
        _list.push_front(kv);
        // 7. 更新哈希表中的迭代器（指向新的头部位置）
        _hash_map[key] = _list.begin();
        // 8. 返回value
        return kv.second;
    }

    // 插入或更新key对应的value
    void put(int key, int value) {
        // 1. 在哈希表中查找key
        auto hash_it = _hash_map.find(key);
        // 2. key已存在：更新value并移动到头部
        if (hash_it != _hash_map.end()) {
            // 获取链表节点迭代器
            auto list_it = hash_it->second;
            // 取出节点并更新value
            pair<int, int> kv = *list_it;
            kv.second = value;
            // 从链表中删除该节点
            _list.erase(list_it);
            // 插入到头部
            _list.push_front(kv);
            // 更新哈希表迭代器
            _hash_map[key] = _list.begin();
        } else {
            // 3. key不存在：插入新节点
            // 检查缓存是否已满
            if (_list.size() >= _capacity) {
                // 缓存已满，淘汰链表尾部节点（最久未使用）
                int delete_key = _list.back().first; // 获取尾部节点的key
                _list.pop_back(); // 删除链表尾部节点
                _hash_map.erase(delete_key); // 删除哈希表中的对应记录
            }
            // 插入新节点到链表头部
            _list.push_front(make_pair(key, value));
            // 在哈希表中添加映射
            _hash_map[key] = _list.begin();
        }
    }

private:
    // 双向链表：存储(key, value)，头部是最近使用，尾部是最久未使用
    list<pair<int, int>> _list;
    // 缓存容量
    size_t _capacity;
    // 哈希表：key -> 链表节点的迭代器，实现O(1)查找
    unordered_map<int, list<pair<int, int>>::iterator> _hash_map;
};

// 测试代码
int main() {
    // 创建容量为2的LRU缓存
    LRUCache cache(2);

    // 执行测试用例（参考LeetCode示例）
    cache.put(1, 1);
    cout << "put(1,1) -> 缓存: [(1,1)]" << endl;

    cache.put(2, 2);
    cout << "put(2,2) -> 缓存: [(2,2), (1,1)]" << endl;

    int res1 = cache.get(1);
    cout << "get(1) -> " << res1 << "，缓存: [(1,1), (2,2)]" << endl; // 输出1

    cache.put(3, 3);
    cout << "put(3,3) -> 淘汰2，缓存: [(3,3), (1,1)]" << endl;

    int res2 = cache.get(2);
    cout << "get(2) -> " << res2 << endl; // 输出-1

    cache.put(4, 4);
    cout << "put(4,4) -> 淘汰1，缓存: [(4,4), (3,3)]" << endl;

    int res3 = cache.get(1);
    cout << "get(1) -> " << res3 << endl; // 输出-1

    int res4 = cache.get(3);
    cout << "get(3) -> " << res4 << "，缓存: [(3,3), (4,4)]" << endl; // 输出3

    int res5 = cache.get(4);
    cout << "get(4) -> " << res5 << "，缓存: [(4,4), (3,3)]" << endl; // 输出4

    return 0;
}

3.2 代码关键细节解析

3.2.1 迭代器的作用

哈希表的 value 存储链表迭代器是整个实现的 "灵魂"------ 迭代器相当于链表节点的 "指针"，通过它可以直接定位到节点，无需遍历链表。当节点在链表中移动位置后，只需更新哈希表中的迭代器，就能保证下一次查找依然是 O (1) 时间。

需要注意的是：std::list的迭代器在节点插入 / 删除后不会失效 （只要节点本身没被删除），这也是选择std::list而不是std::vector的重要原因 ------std::vector的迭代器在插入时可能因扩容失效，无法满足我们的需求。

3.2.2 链表节点的移动逻辑

无论是 get 还是 put 操作，只要数据被访问或更新，就需要移动到链表头部，这是 LRU "最近使用" 规则的体现。移动过程分为 "删除原节点" 和 "插入头部" 两步，都是 O (1) 时间，不会影响整体效率。

3.2.3 缓存淘汰逻辑

当缓存已满时，直接删除链表尾部节点 ------ 因为链表尾部是最久未使用的数据，这完全符合 LRU 的淘汰规则。删除时必须同时删除哈希表中的对应记录，否则会出现 "哈希表中有 key，但链表中无节点" 的不一致情况。

3.3 测试结果验证

运行上面的测试代码，输出如下：

复制代码

put(1,1) -> 缓存: [(1,1)]
put(2,2) -> 缓存: [(2,2), (1,1)]
get(1) -> 1，缓存: [(1,1), (2,2)]
put(3,3) -> 淘汰2，缓存: [(3,3), (1,1)]
get(2) -> -1
put(4,4) -> 淘汰1，缓存: [(4,4), (3,3)]
get(1) -> -1
get(3) -> 3，缓存: [(3,3), (4,4)]
get(4) -> 4，缓存: [(4,4), (3,3)]

结果与 LeetCode 示例是完全一致，证明我们的实现是正确的。

四、深入理解：LRU 的时间复杂度与空间复杂度

4.1 时间复杂度分析

我们的实现中，get 和 put 操作的每一步都是 O (1) 时间复杂度：

哈希表查找、插入、删除 ：O (1)（std::unordered_map的平均时间复杂度）；

双向链表插入、删除：O (1)（通过迭代器直接操作，无需遍历）；

节点移动：本质是 "删除 + 插入"，两步都是 O (1)。

因此，get 和 put 操作的时间复杂度均为 O (1)，这是 LRU 最理想的效率表现。

4.2 空间复杂度分析

空间复杂度由缓存容量决定：

双向链表存储的节点数最多为**_capacity**，空间复杂度 O (capacity)；

哈希表存储的键值对数量与链表节点数一致，空间复杂度 O (capacity)；

整体空间复杂度为 O (capacity)，没有额外的空间开销。

4.3 与其他实现方式的对比

除了 "双向链表 + 哈希表"，还有几种常见的 LRU 实现方式，但效率都不如我们的方案：

仅用双向链表：查找需要遍历，时间复杂度 O (n)，适合小容量缓存；

数组 + 时间戳：用数组存储数据，每个元素记录最后访问时间，淘汰时遍历找时间戳最小的元素，时间复杂度 O (n)；

平衡二叉搜索树 + 哈希表 ：比如用std::map（红黑树）维护访问顺序，哈希表查找，时间复杂度 O (log n)，实现复杂，不如双向链表高效。

"双向链表 + 哈希表" 的组合是时间和实现复杂度的最优解，也是工业界的标准实现方式。

五、LRU 的实际应用场景

LRU 的应用场景远比我们想象的广泛，从底层系统到上层应用，都能看到它的身影：

5.1 操作系统中的 LRU

页面置换算法：操作系统为了减少磁盘 IO，会将部分内存页面缓存起来，当内存不足时，使用 LRU 算法淘汰最久未使用的页面；

CPU 缓存替换：CPU 的一级、二级缓存容量有限，当新指令或数据需要缓存时，用 LRU 淘汰最久未使用的缓存行。

5.2 数据库中的 LRU

MySQL 缓冲池（Buffer Pool）：MySQL 会将磁盘上的表数据和索引缓存到内存的 Buffer Pool 中，采用 LRU 算法管理缓存页，提高查询效率；

Redis 缓存：Redis 的过期策略中，除了定期删除，还会结合 LRU 算法淘汰过期键（volatile-lru 策略）。

5.3 框架与应用中的 LRU

浏览器缓存：浏览器的本地存储（LocalStorage）和会话存储（SessionStorage）会使用 LRU 算法管理缓存数据，当存储容量满时，淘汰最久未使用的条目；

框架缓存 ：Spring Boot 的@Cacheable注解、MyBatis 的一级缓存，默认都支持 LRU 缓存策略；

自定义本地缓存：在高并发场景中，开发者会基于 LRU 实现本地缓存，减少对分布式缓存的访问压力。

5.4 面试中的 LRU

LRU 是面试中的 "高频考点"，常见问题包括：

设计一个 O (1) 时间复杂度的 LRU 缓存（手写代码）；

LRU 和 LFU 的区别与实现；

Redis 中的 LRU 优化（Redis 采用的是近似 LRU，通过随机采样实现，而非精确 LRU）。

掌握本文的实现思路，就能轻松应对这类面试题。

六、常见问题与优化方向

6.1 线程安全问题

我们的实现是非线程安全的，在单线程环境（如 LeetCode 测试）中完全没问题，但在多线程环境（如高并发服务）中会出现数据竞争。

解决方案：

加锁：使用std::mutex对 get 和 put 操作加锁，保证同一时间只有一个线程操作缓存；

无锁实现 ：使用原子操作 （std::atomic）和 CAS（Compare And Swap）机制，实现无锁 LRU，适合高并发场景。

示例（加锁版 get 操作）：