Cyber骇客的树状逻辑数据——【初阶数据结构与算法】树

---

🎥个人简介
🌊🌉🌊心手合一，水到渠成

点击下面查看作者专栏 🏞️🏞️作者主页🏞️🏞️ 🔥🔥C语言专栏🔥🔥 🌊🌊编程百度🌊🌊 🌠🌠如何获取自己的代码仓库🌠🌠

---

索引与导读

• 树的基础概念
• • 1）什么是树？
  • 2）核心术语 (Terminology)
  • 3）树(Tree)的四种主要表示法 (C语言实现)
  • • 3.1）双亲表示法
    • 3.2）孩子表示法
    • 3.3）孩子双亲表示法
    • 3.4）孩子兄弟表示法（最重要！！！）
  • 树在实际中的运用
  • 后续预告
• [💻结尾--- 核心连接协议](#💻结尾— 核心连接协议)

树的基础概念

1）什么是树？

树（Tree）是一种非线性 的数据结构，它是由 n ( n ≥ 0 ) n (n \ge 0) n(n≥0) 个节点组成的有限集合。

• 如果 n = 0 n=0 n=0，称为空树。
• 如果 n > 0 n > 0 n>0，这棵树满足以下条件：
  1. 有一个特定的节点被称为根节点 (Root)。
  2. 其余节点被分成 m ( m ≥ 0 ) m (m \ge 0) m(m≥0) 个互不相交的集合 T 1 , T 2 , . . . , T m T_1, T_2, ..., T_m T1,T2,...,Tm，其中每一个集合本身又是一棵树，称为根的子树 (Subtree)

核心逻辑： 树是递归定义的

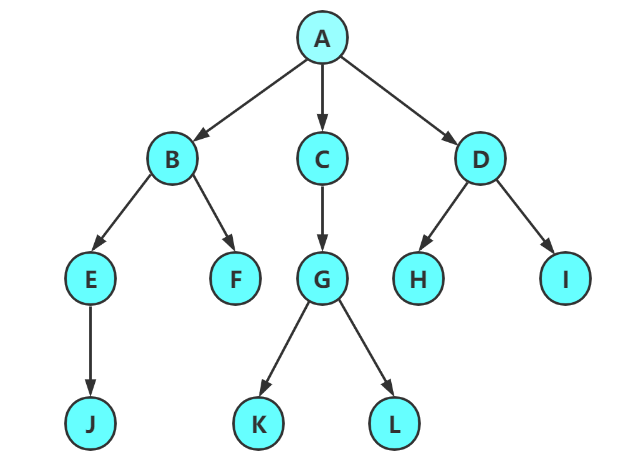
注意： 树形结构中，子树之间不能有交集，否则就不是树形结构

---

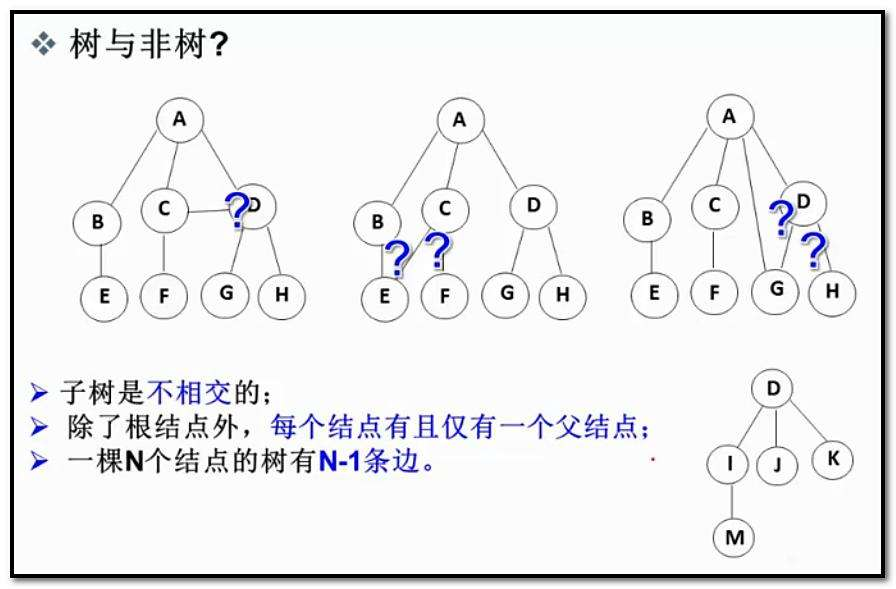
2）核心术语 (Terminology)

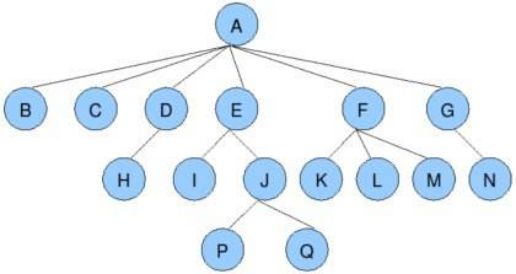
术语	解释	示例（对应上图）
🚩结点的度	一个结点含有的子树的个数称为该结点的度；	如上图：A的为6
🚩叶结点或终端结点	度为0的结点称为叶结点；	如上图：B、C、H、I...等结点为叶结点
🚩非终端结点或分支结点	度不为0的结点；	如上图：D、E、F、G...等结点为分支结点
🚩双亲结点或父结点	若一个结点含有子结点，则这个结点称为其子结点的父结点；	如上图：A是B的父结点
🚩孩子结点或子结点	一个结点含有的子树的根结点称为该结点的子结点；	如上图：B是A的孩子结点
🚩兄弟结点	具有相同父结点的结点互称为兄弟结点；	如上图：B、C是兄弟结点
🚩树的度	一棵树中，最大的结点的度称为树的度；	如上图：树的度为6
🚩结点的层次	从根开始定义起，根为第1层，根的子结点为第2层，以此类推；
🚩树的高度或深度	树中结点的最大层次；	如上图：树的高度为4
🚩堂兄弟结点	双亲在同一层的结点互为堂兄弟；	如上图：H、I互为兄弟结点
🚩结点的祖先	从根到该结点所经分支上的所有结点；	如上图：A是所有结点的祖先
🚩子孙	以某结点为根的子树中任一结点都称为该结点的子孙。	如上图：所有结点都是A的子孙
🚩森林	由m（m>0）棵互不相交的树的集合称为森林；

---

3）树(Tree)的四种主要表示法 (C语言实现)

在数据结构中，树（Tree） 是一种非常重要的非线性结构，相比于线性结构，树结构的分支更为复杂，多条分支之间的层级和嵌套关系决定了其存储表示通常更为繁琐

🚩1. 双亲表示法

🚩2. 孩子表示法

🚩3. 孩子双亲表示法

🚩4. 孩子兄弟表示法

3.1）双亲表示法

双亲表示法利用了 顺序存储（数组） 。树中的每个节点不仅存储自己的数据，还存储其父节点在数组中的下标。

• 优点 ：查找某个节点的父节点（Parent）非常快，时间复杂度为 O ( 1 ) O(1) O(1)
• 缺点：查找某个节点的孩子节点需要遍历整个数组，比较耗时

• 代码实现

#include <stdio.h>
#define MAX_TREE_SIZE 100

/* 树的节点定义 */
typedef struct PTNode {
    int data;       // 节点数据
    int parent;     // 双亲位置（数组下标）
} PTNode;

/* 树的结构定义 */
typedef struct {
    PTNode nodes[MAX_TREE_SIZE]; // 节点数组
    int r;                       // 根的位置
    int n;                       // 节点总数
} PTree;

3.2）孩子表示法

#define MAX_TREE_SIZE 100
typedef int TElemType;

// 1. 孩子链表节点
typedef struct CTNode {
    int child;             // 孩子节点在数组中的下标
    struct CTNode *next;   // 指向下一个孩子节点的指针
} *ChildPtr;

// 2. 表头数组节点
typedef struct {
    TElemType data;        // 存放在树中的节点数据
    ChildPtr firstchild;   // 指向第一个孩子的指针
} CTBox;

// 3. 树结构
typedef struct {
    CTBox nodes[MAX_TREE_SIZE]; // 节点数组
    int r, n;                   // 根的位置和节点数
} CTree;

3.3）孩子双亲表示法

🚩为了解决孩子表示法"找爹难"的问题。我们需要做的改进很简单：在表头数组中，额外增加一个空间，存储该节点的双亲下标

#define MAX_TREE_SIZE 100
typedef int TElemType;

// 孩子链表节点（不变）
typedef struct CTNode {
    int child;
    struct CTNode *next;
} *ChildPtr;

// 表头数组节点（增加parent域）
typedef struct {
    TElemType data;
    int parent;            // <--- 新增：双亲在数组中的下标
    ChildPtr firstchild;   // 指向第一个孩子的指针
} CTBox;

// 树结构
typedef struct {
    CTBox nodes[MAX_TREE_SIZE];
    int r, n;
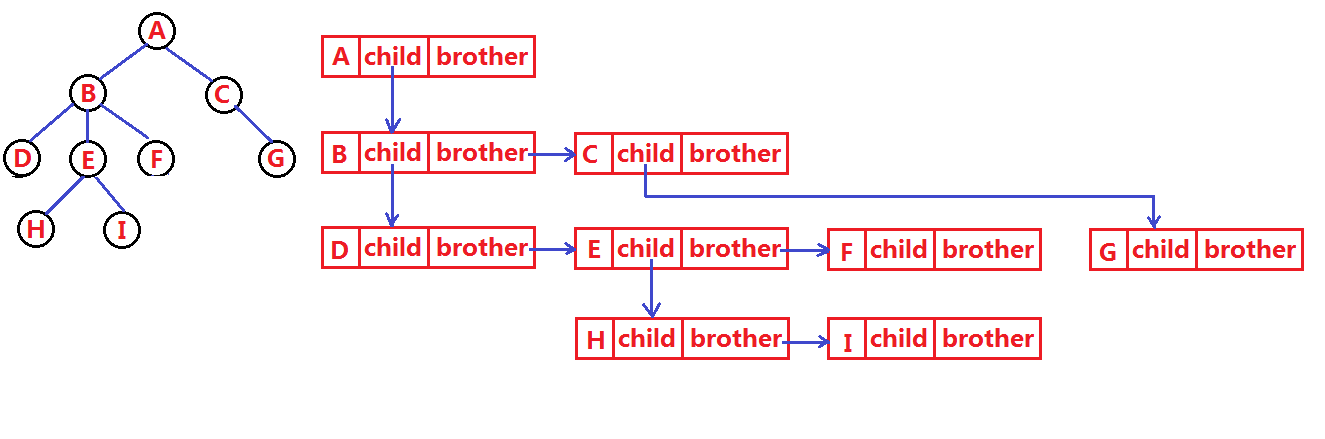
} CPTree;

3.4）孩子兄弟表示法（最重要！！！）

❗这是最重要的一种表示法，又称为二叉链表表示法

它体现了树和二叉树转换的核心思想

任意一棵树，它的节点的第一个孩子如果存在就是唯一的，它的右兄弟如果存在也是唯一的

设置两个指针：

• firstchild： 指向该节点的第一个孩子。

• nextsibling： 指向该节点的下一个右兄弟。

👄口诀： 左孩子，右兄弟

4.2 C语言代码实现

typedef int TElemType;

typedef struct CSNode {
    TElemType data;                 // 数据域
    struct CSNode *firstchild;      // 指向第一个孩子
    struct CSNode *nextsibling;     // 指向右兄弟
} CSNode, *CSTree;

以由上到下 ，然后每一层从左到右 的方法链接节点

---

树在实际中的运用

---

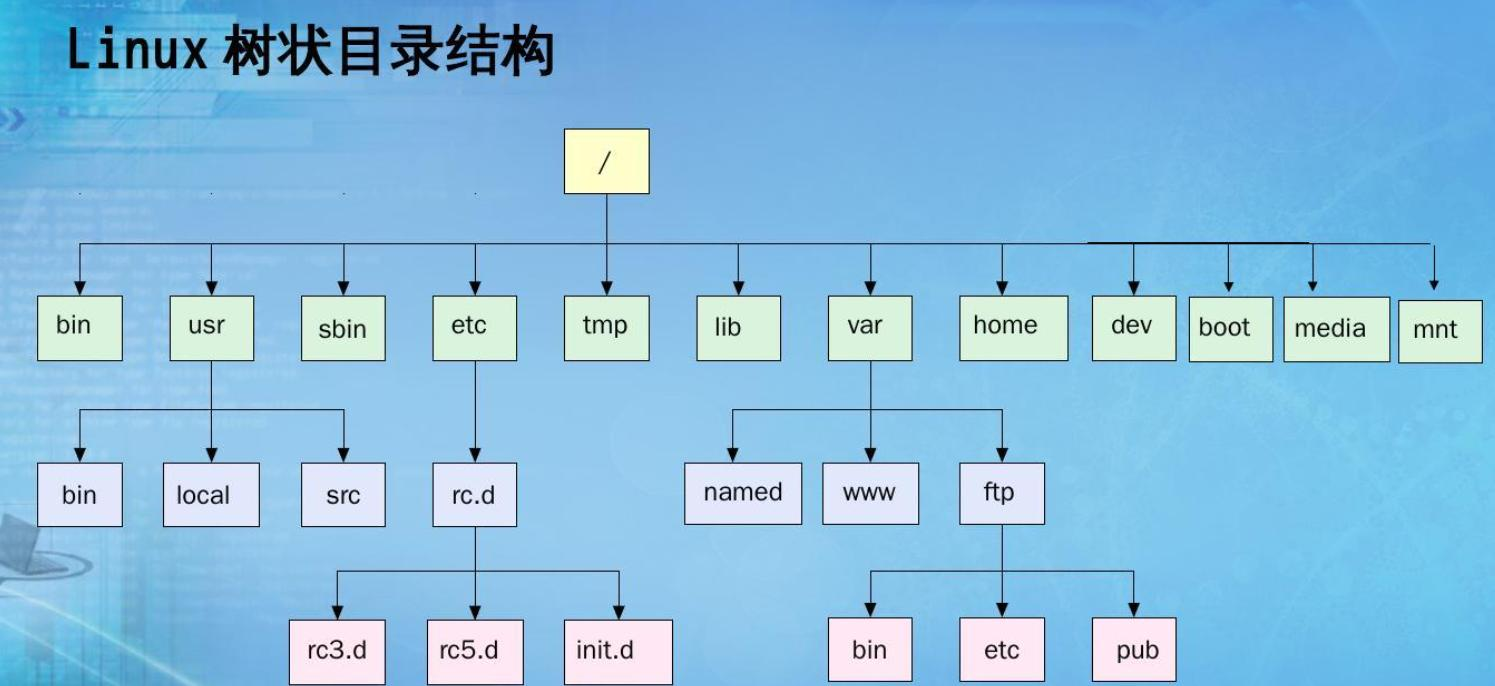
后续预告

🎯在下面两章我们会在树的基础上讲解堆与二叉树，敬请期待哦~

---

💻结尾--- 核心连接协议

警告： 🌠🌠正在接入底层技术矩阵。如果你已成功破解学习中的逻辑断层，请执行以下指令序列以同步数据：🌠🌠

---

【📡】 建立深度链接： 关注本终端。在赛博丛林中深耕底层架构，从原始代码到进阶协议，同步见证每一次系统升级。

【⚡】 能量过载分发： 执行点赞操作。通过高带宽分发，让优质模组在信息流中高亮显示，赋予知识跨维度的传播力。

【💾】 离线缓存核心： 将本页加入收藏。把这些高频实战逻辑存入你的离线存储器，在遭遇系统崩溃或需要离线检索时，实现瞬时读取。

【💬】 协议加密解密： 在评论区留下你的散列码。分享你曾遭遇的代码冲突或系统漏洞（那些年踩过的坑），通过交互式编译共同绕过技术陷阱。

【🛰️】 信号频率投票： 通过投票发射你的选择。你的每一次点击都在重新定义矩阵的进化方向，决定下一个被全量拆解的技术节点。

---