强化学习2.2 MDP实践——Frozen lake

问题介绍

FrozenLake 指 OpenAI Gym 库中的一个经典强化学习环境。

• 游戏场景：玩家控制角色在一个由冰冻湖面组成的网格世界中移动，目标是从起点到达终点，同时避免掉入冰面上的洞穴。网格通常为正方形，如 4x4 或 8x8 的地图，每个方格可以是起点、终点、冰冻区域或洞穴。
• 动作空间：动作的形状是（1，）的 int64 变量，在范围 {0，3} 内，表示玩家应该向哪个方向移动。其中 0 为向左移动，1 为向下移动，2 为向右移动，3 为向上移动。
• 观察空间：观察值是一个 int 值，代表玩家的当前位置，计算方式为 current_row * nrows + current_col（其中行和列都从 0 开始）。例如，在 4x4 地图中的目标位置可以这样计算：3 * 4 + 3 = 15。
• 初始状态：游戏开始时，玩家处于状态 [0]，即地图的左上角位置 [0,0]。
• 奖励机制：达到目标获得奖励 + 1，掉入洞中或到达冰冻区域奖励为 0。
• 游戏结束条件：玩家掉入洞中或到达目标位置时，游戏终止；若使用时间限制包装器，对于 4x4 环境，情节长度为 100 步，对于 8x8 环境，情节长度为 200 步，达到步数限制时游戏结束。

使用MDP解决问题

初始化环境

from mdp import FrozenLakeEnv
mdp = FrozenLakeEnv(slip_chance=0)

mdp.render()

如下图所示，F表示正常的道路，H表示洞，G表示终点。

定义价值迭代函数

def value_iteration(mdp, state_values=None, gamma=0.9, num_iter=1000, min_difference=1e-5):
    """ performs num_iter value iteration steps starting from state_values. Same as before but in a function """
    state_values = state_values or {s: 0 for s in mdp.get_all_states()}
    for i in range(num_iter):

        # 计算新的状态价值：对每个状态，取所有动作的最大期望回报
        new_state_values = {}
        for s in mdp.get_all_states():
            # 终端状态（无可用动作）的价值保持为0
            if mdp.is_terminal(s):
                new_state_values[s] = 0.0
                continue
            # 遍历所有可能的动作，计算每个动作的期望回报
            action_values = []
            for a in mdp.get_possible_actions(s):
                q_val = 0.0
                # 遍历该动作下的所有转移概率和后续状态
                for prob, next_s, reward in mdp.get_transitions(s, a):
                    q_val += prob * (reward + gamma * state_values[next_s])
                action_values.append(q_val)
            # 取最大的动作价值作为当前状态的新价值
            new_state_values[s] = max(action_values)

        assert isinstance(new_state_values, dict)

        # 计算与上一轮价值的最大差异
        diff = max(abs(new_state_values[s] - state_values[s])
                   for s in mdp.get_all_states())

        print("iter %4i   |   diff: %6.5f   |   V(start): %.3f " %
              (i, diff, new_state_values[mdp._initial_state]))

        state_values = new_state_values
        if diff < min_difference:
            break

    return state_values

进行价值迭代

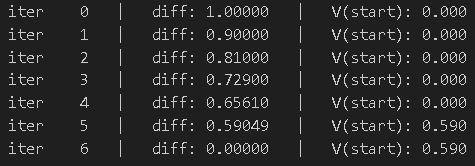
state_values = value_iteration(mdp)

下面展示运行过程

根据当前状态和动作计算累计奖励

def get_action_value(mdp, state_values, state, action, gamma):
    """ Computes Q(s,a) as in formula above """
    q_value = 0.0
    # 获取从state执行action后所有可能的下一状态
    next_states = mdp.get_next_states(state, action)
    
    for next_state in next_states:
        # 获取转移概率 P(s'|s,a)
        prob = mdp.get_transition_prob(state, action, next_state)
        # 获取即时奖励 r(s,a,s')
        reward = mdp.get_reward(state, action, next_state)
        # 累加计算 Q(s,a) = sum[ P(s'|s,a) * (r + gamma*V(s')) ]
        q_value += prob * (reward + gamma * state_values[next_state])
    
    return q_value

根据当前状态选择最优动作

def get_optimal_action(mdp, state_values, state, gamma=0.9):
    """ Finds optimal action using formula above. """
    if mdp.is_terminal(state):
        return None

    # 获取当前状态下所有可能的动作
    possible_actions = mdp.get_possible_actions(state)
    
    # 计算每个动作的Q值，存储为 {动作: Q值}
    action_q = {}
    for action in possible_actions:
        q_value = get_action_value(mdp, state_values, state, action, gamma)
        action_q[action] = q_value
    
    # 选择Q值最大的动作（argmax_a Q(s,a)）
    optimal_action = max(action_q, key=action_q.get)
    
    return optimal_action

下面展示通过价值迭代函数所得到的状态价值，进行游戏的过程

s = mdp.reset()
mdp.render()
for t in range(100):
    a = get_optimal_action(mdp, state_values, s, gamma=0.9)
    print(a, end='\n\n')
    s, r, done, _ = mdp.step(a)
    mdp.render()
    if done:
        break

角色依据状态价值进行运动的过程如下所示

下面进行可视化，定义函数

import matplotlib.pyplot as plt
%matplotlib inline


def draw_policy(mdp, state_values):
    plt.figure(figsize=(3, 3))
    h, w = mdp.desc.shape
    states = sorted(mdp.get_all_states())
    V = np.array([state_values[s] for s in states])
    Pi = {s: get_optimal_action(mdp, state_values, s, gamma) for s in states}
    plt.imshow(V.reshape(w, h), cmap='gray', interpolation='none', clim=(0, 1))
    ax = plt.gca()
    ax.set_xticks(np.arange(h)-.5)
    ax.set_yticks(np.arange(w)-.5)
    ax.set_xticklabels([])
    ax.set_yticklabels([])
    Y, X = np.mgrid[0:4, 0:4]
    a2uv = {'left': (-1, 0), 'down': (0, -1), 'right': (1, 0), 'up': (0, 1)}
    for y in range(h):
        for x in range(w):
            plt.text(x, y, str(mdp.desc[y, x].item()),
                     color='g', size=12,  verticalalignment='center',
                     horizontalalignment='center', fontweight='bold')
            a = Pi[y, x]
            if a is None:
                continue
            u, v = a2uv[a]
            plt.arrow(x, y, u*.3, -v*.3, color='m',
                      head_width=0.1, head_length=0.1)
    plt.grid(color='b', lw=2, ls='-')
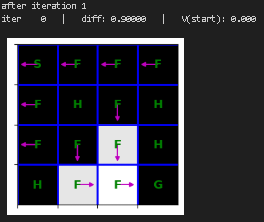
    plt.show()

重新训练价值迭代函数并进行可视化

state_values = {s: 0 for s in mdp.get_all_states()}

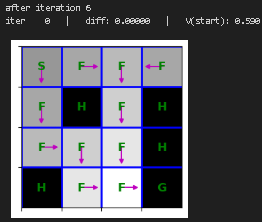
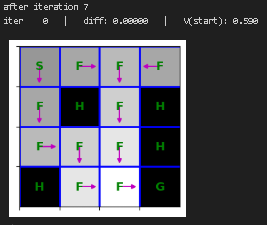
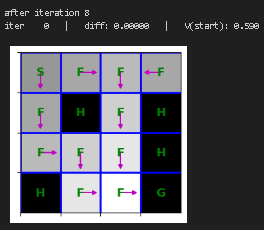
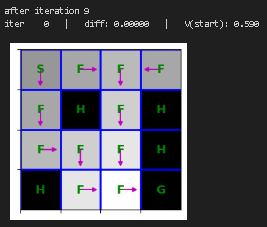
for i in range(10):
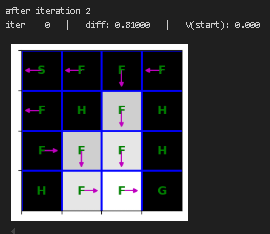
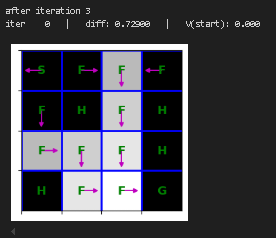
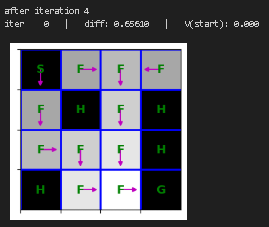
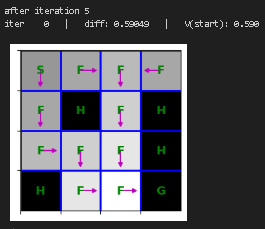
    print("after iteration %i" % i)
    state_values = value_iteration(mdp, state_values, num_iter=1)
    draw_policy(mdp, state_values)
# please ignore iter 0 at each step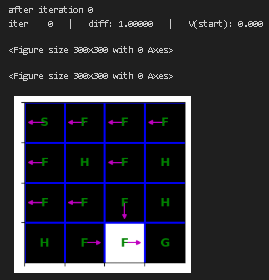

定义8*8的问题，并进行可视化

from IPython.display import clear_output
from time import sleep
mdp = FrozenLakeEnv(map_name='8x8', slip_chance=0.1)
state_values = {s: 0 for s in mdp.get_all_states()}

for i in range(30):
    clear_output(True)
    print("after iteration %i" % i)
    state_values = value_iteration(mdp, state_values, num_iter=1)
    draw_policy(mdp, state_values)
    sleep(0.5)
# please ignore iter 0 at each step

整体迭代过程如下所示

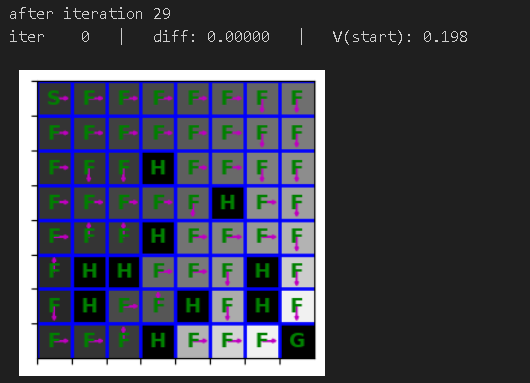
大规模测试

连续跑1000次进行测试

mdp = FrozenLakeEnv(slip_chance=0)
state_values = value_iteration(mdp)

total_rewards = []
for game_i in range(1000):
    s = mdp.reset()
    rewards = []
    for t in range(100):
        s, r, done, _ = mdp.step(
            get_optimal_action(mdp, state_values, s, gamma=0.9))
        rewards.append(r)
        if done:
            break
    total_rewards.append(np.sum(rewards))

print("average reward: ", np.mean(total_rewards))
assert(1.0 <= np.mean(total_rewards) <= 1.0)
print("Well done!")

迭代过程如下

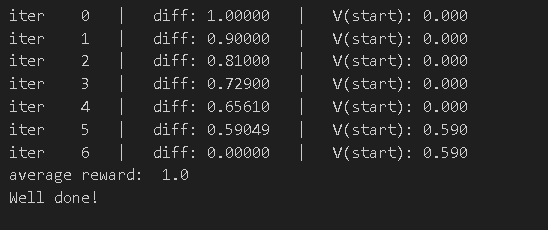
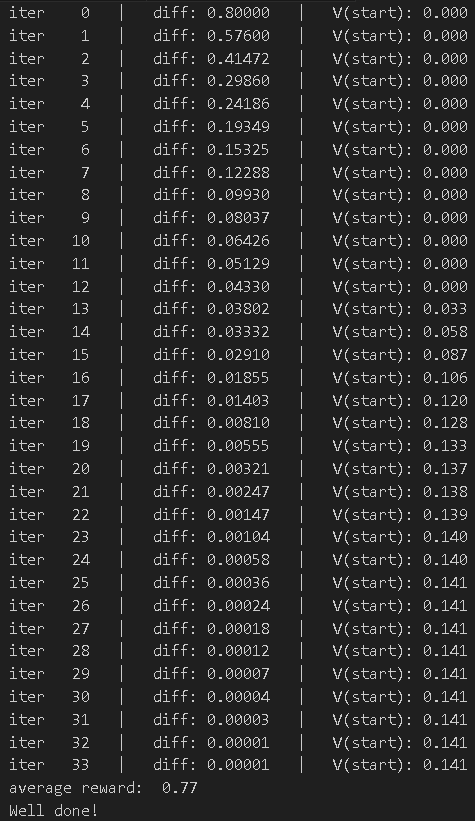
调整slip_chance重新进行测试,打滑概率为10%

# Measure agent's average reward
mdp = FrozenLakeEnv(slip_chance=0.1)
state_values = value_iteration(mdp)

total_rewards = []
for game_i in range(1000):
    s = mdp.reset()
    rewards = []
    for t in range(100):
        s, r, done, _ = mdp.step(
            get_optimal_action(mdp, state_values, s, gamma=0.9))
        rewards.append(r)
        if done:
            break
    total_rewards.append(np.sum(rewards))

print("average reward: ", np.mean(total_rewards))
assert(0.8 <= np.mean(total_rewards) <= 0.95)
print("Well done!")

迭代过程如下

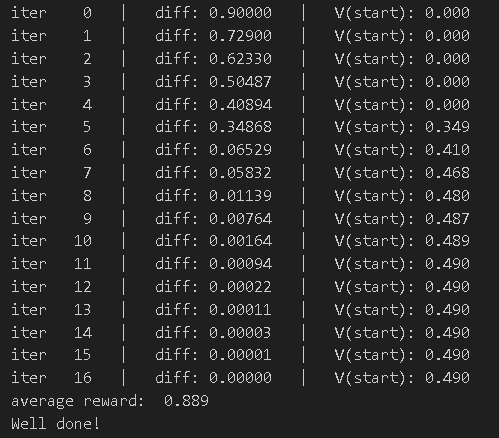
继续调整slip_chance重新进行测试,打滑概率为25%

# Measure agent's average reward
mdp = FrozenLakeEnv(slip_chance=0.25)
state_values = value_iteration(mdp)

total_rewards = []
for game_i in range(1000):
    s = mdp.reset()
    rewards = []
    for t in range(100):
        s, r, done, _ = mdp.step(
            get_optimal_action(mdp, state_values, s, gamma=0.9))
        rewards.append(r)
        if done:
            break
    total_rewards.append(np.sum(rewards))

print("average reward: ", np.mean(total_rewards))
assert(0.6 <= np.mean(total_rewards) <= 0.7)
print("Well done!")

迭代过程如下

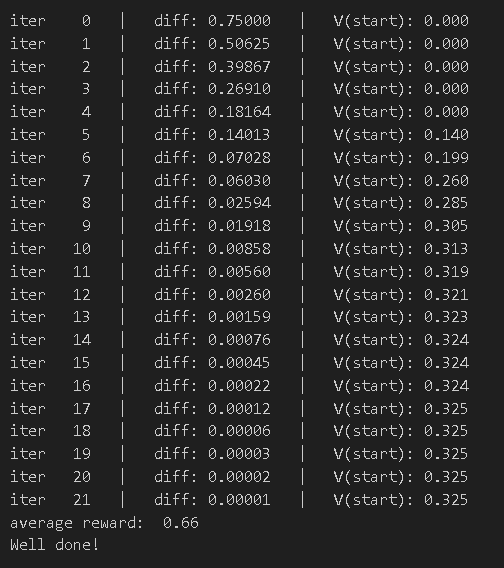
改为8*8的问题规模，定义打滑概率为20%

# Measure agent's average reward
mdp = FrozenLakeEnv(slip_chance=0.2, map_name='8x8')
state_values = value_iteration(mdp)

total_rewards = []
for game_i in range(1000):
    s = mdp.reset()
    rewards = []
    for t in range(100):
        s, r, done, _ = mdp.step(
            get_optimal_action(mdp, state_values, s, gamma=0.9))
        rewards.append(r)
        if done:
            break
    total_rewards.append(np.sum(rewards))

print("average reward: ", np.mean(total_rewards))
assert(0.6 <= np.mean(total_rewards) <= 0.8)
print("Well done!")

迭代过程如下