引言
快速排序到底有多块?通过实验对各种排序算法做了对比(单位:毫秒),对比结果如下表所示。
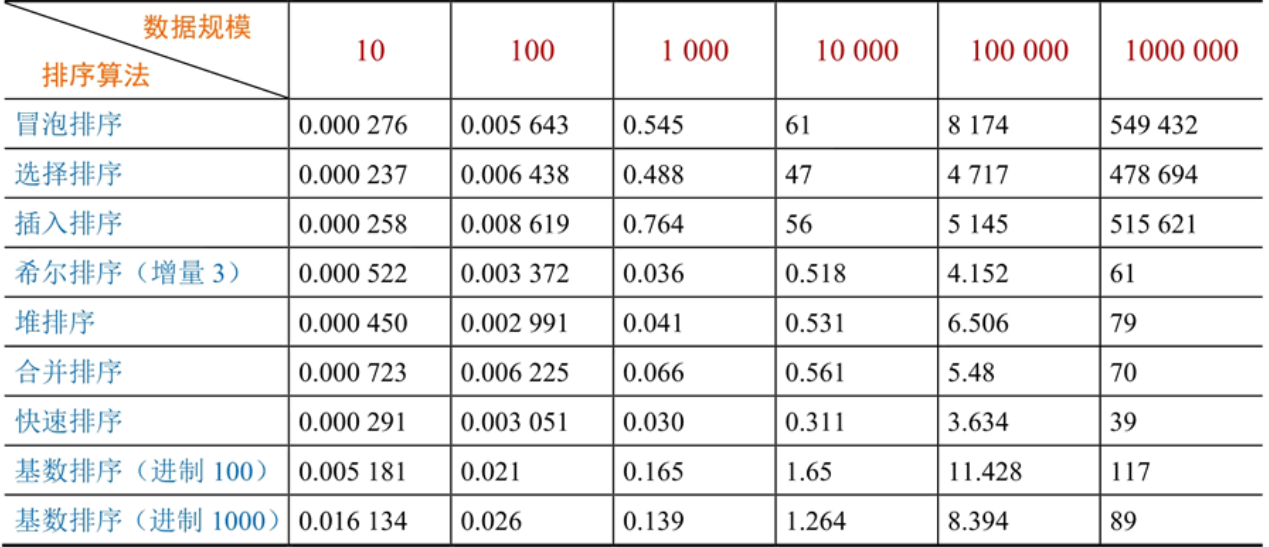
由此可见面对大量数据快速排序的速度是冒泡排序速度的数千倍,那么今天就来学习快速排序的过程思路和代码实现。
一、快速排序算法概述
快速排序是由Tony Hoare在1960年提出的一种高效的排序算法,采用分治策略。其核心思想是:选择一个基准元素,通过一趟排序将待排记录分割成独立的两部分,其中一部分的所有数据都比另一部分的所有数据小,然后再按此方法对这两部分数据分别进行快速排序。
基本特性:
平均时间复杂度:O(nlogn) 最坏时间复杂度:O(n²) 最好情况:O(nlogn)
空间复杂度:O(logn) 稳定性:不稳定排序
二、挖坑法快速排序原理
2.1 挖坑法基本思想
挖坑法是快速排序的一种实现方式,其核心思路是:
-
选取一个基准值(pivot),默认以最左边的值为基准值
-
将基准值的位置作为第一个"坑"
-
从右向左找比基准值小的放在坑位,再从左向右找比基准值大的放在坑位,每找到一次满足条件的数切换一下左右,一直循环直到左指针遇到右指针
-
最终将基准值放入最后一个坑位
-
再以基准值放入的坑位为分界线,分成若干个数据段再对每个数据段进行上面的排序
2.2 排序过程图解
以数组 [5, 3, 8, 6, 2, 7, 1, 4] 为例:
初始: [5, 3, 8, 6, 2, 7, 1, 4]
↑ ↑
left right
pivot=5, 坑在left位置
步骤1: 从右向左找小于5的数,找到4
[_, 3, 8, 6, 2, 7, 1, 4] → [4, 3, 8, 6, 2, 7, 1, _]
坑移到right位置
步骤2: 从左向右找大于5的数,找到8
[4, 3, _, 6, 2, 7, 1, 8] → 坑移到原8的位置
继续交替扫描,最终将5放入正确位置...三、递归实现挖坑法快速排序
#include <stdio.h>
void quickSortRecursive(int arr[], int left, int right) {
if (left >= right) return;
int i = left, j = right, pivot = arr[left];
while (i < j) {
while (i < j && arr[j] >= pivot) j--;
if (i < j) arr[i++] = arr[j];
while (i < j && arr[i] <= pivot) i++;
if (i < j) arr[j--] = arr[i];
}
arr[i] = pivot;
quickSortRecursive(arr, left, i - 1);
quickSortRecursive(arr, i + 1, right);
}
void printArray(int arr[], int n) {
for (int i = 0; i < n; i++) printf("%d ", arr[i]);
printf("\n");
}
int main() {
int arr[] = {5, 3, 8, 6, 2, 7, 1, 4};
int n = sizeof(arr) / sizeof(arr[0]);
printf("原数组: ");
printArray(arr, n);
quickSortRecursive(arr, 0, n - 1);
printf("排序后: ");
printArray(arr, n);
return 0;
}四、非递归实现挖坑法快速排序
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100
typedef struct Stack {
int data[MAX_SIZE];
int top;
} Stack;
void push(Stack *s, int x) {
if (s->top < MAX_SIZE - 1) s->data[++s->top] = x;
}
int pop(Stack *s) {
if (s->top >= 0) return s->data[s->top--];
return -1;
}
int isEmpty(Stack *s) {
return s->top == -1;
}
void quickSortNonRecursive(int arr[], int left, int right) {
Stack s; s.top = -1;
push(&s, left); push(&s, right);
while (!isEmpty(&s)) {
int r = pop(&s); int l = pop(&s);
if (l >= r) continue;
int i = l, j = r, pivot = arr[l];
while (i < j) {
while (i < j && arr[j] >= pivot) j--;
if (i < j) arr[i++] = arr[j];
while (i < j && arr[i] <= pivot) i++;
if (i < j) arr[j--] = arr[i];
}
arr[i] = pivot;
push(&s, l); push(&s, i - 1);
push(&s, i + 1); push(&s, r);
}
}
int main() {
int arr[] = {5, 3, 8, 6, 2, 7, 1, 4};
int n = sizeof(arr) / sizeof(arr[0]);
printf("原数组: ");
for (int i = 0; i < n; i++) printf("%d ", arr[i]);
printf("\n");
quickSortNonRecursive(arr, 0, n - 1);
printf("非递归排序后: ");
for (int i = 0; i < n; i++) printf("%d ", arr[i]);
printf("\n");
return 0;
}五、快速排序的优化策略
5.1 三数取中法选择基准
int getMidIndex(int arr[], int left, int right) {
int mid = left + (right - left) / 2;
if (arr[left] > arr[mid]) {
if (arr[mid] > arr[right]) return mid;
else if (arr[left] > arr[right]) return right;
else return left;
} else {
if (arr[left] > arr[right]) return left;
else if (arr[mid] > arr[right]) return right;
else return mid;
}
}5.2 小区间量使用直接插入排序
void insertSort(int arr[], int left, int right) {
for (int i = left + 1; i <= right; i++) {
int key = arr[i], j = i - 1;
while (j >= left && arr[j] > key) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;
}
}
void optimizedQuickSort(int arr[], int left, int right) {
if (right - left <= 10) {
insertSort(arr, left, right);
return;
}
int mid = getMidIndex(arr, left, right);
int temp = arr[left]; arr[left] = arr[mid]; arr[mid] = temp;
int i = left, j = right, pivot = arr[left];
while (i < j) {
while (i < j && arr[j] >= pivot) j--;
if (i < j) arr[i++] = arr[j];
while (i < j && arr[i] <= pivot) i++;
if (i < j) arr[j--] = arr[i];
}
arr[i] = pivot;
optimizedQuickSort(arr, left, i - 1);
optimizedQuickSort(arr, i + 1, right);
}六、复杂度分析与比较
6.1 时间复杂度分析
最好情况:O(nlogn) - 每次划分都很均匀
平均情况:O(nlogn)
最坏情况:O(n²) - 数组已排序或逆序
6.2 空间复杂度分析
递归版本:O(logn) - 递归调用栈深度
非递归版本:O(logn) - 手动维护的栈空间
6.3 稳定性分析
快速排序是不稳定的排序算法,因为相同元素的相对位置可能在分区过程中改变。
七、递归与非递归版本比较
| 特性 | 递归版本 | 非递归版本 |
|---|---|---|
| 代码复杂度 | 简单易懂 | 相对复杂 |
| 栈空间 | 系统栈,可能溢出 | 手动控制,更安全 |
| 性能 | 函数调用开销 | 无函数调用开销 |
| 调试难度 | 较难调试 | 相对容易调试 |
八、使用场景与选择建议
8.1 选择递归版本的情况:
数据规模不是特别大 代码简洁性更重要 栈深度不会太大
8.2 选择非递归版本的情况:
数据规模很大,担心栈溢出 对性能有极致要求 需要更好的调试体验
8.3 选择优化版本的情况:
数据可能部分有序 对性能稳定性要求高 处理大数据集
九、注意事项与最佳实践
-
边界处理:始终检查left < right
-
基准选择:避免最坏情况,使用三数取中
-
递归深度:大数据集考虑非递归版本
-
内存使用:注意栈空间限制
-
稳定性:需要稳定排序时选择其他算法
十、常见面试题
10.1 基础概念题
-
快速排序的时间复杂度是多少?最坏情况如何避免?
-
为什么快速排序是不稳定的?
-
快速排序和归并排序的主要区别是什么?
10.2 编码实现题
// 题目1:单链表快速排序
struct ListNode {
int val;
struct ListNode *next;
};
struct ListNode* quickSortList(struct ListNode* head) {
if (!head || !head->next) return head;
int pivot = head->val;
struct ListNode *less = NULL, *equal = NULL, *greater = NULL;
struct ListNode **l = &less, **e = &equal, **g = &greater;
while (head) {
if (head->val < pivot) { *l = head; l = &(*l)->next; }
else if (head->val == pivot) { *e = head; e = &(*e)->next; }
else { *g = head; g = &(*g)->next; }
head = head->next;
}
*l = *e = *g = NULL;
less = quickSortList(less);
greater = quickSortList(greater);
struct ListNode *result = less;
while (less && less->next) less = less->next;
if (less) less->next = equal;
else result = equal;
while (equal && equal->next) equal = equal->next;
if (equal) equal->next = greater;
else result = greater;
return result;
}10.3 算法分析题
-
给定10^6个整数,如何选择快速排序的优化策略?
-
如何在O(n)时间内找到数组的第k大元素?
-
快速排序在什么情况下会退化为O(n²)?如何检测这种情况?
总结
快速排序是实践中最高效的排序算法之一,掌握其挖坑法实现及各种优化技巧对于程序员至关重要。递归版本代码简洁,非递归版本更安全可靠,优化版本能处理各种边界情况。在实际应用中,应根据具体场景选择合适的实现方式,并注意算法的时间、空间复杂度以及稳定性要求。