目录
摘要
继续承接上周吴恩达老师的机器学习课程,主要学习的是在一个单层中我们如何实现前向传播,并且要理解神经网络是如何高效实现的
Abstract
Continuing from Professor Andrew Ng's machine learning course last week, the main focus is on how we implement forward propagation in a single layer and to understand how neural networks are efficiently implemented.
一、在一个单层中的前向传播
我们将继续使用咖啡烘焙模型来讨论在一个单层中的前向传播
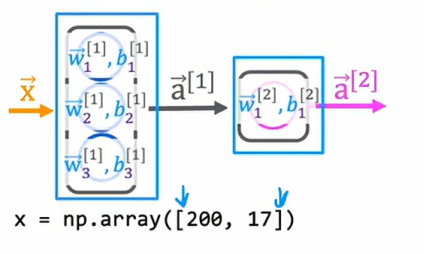
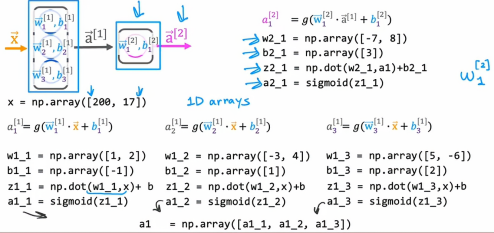
让我们看看如何获取输入特征向量x并实现前向传播以得到输出a2,我将使用一维数组来表示所有这些向量和参数,这是Python中的一维数组而不是二维矩阵,因为括号内只有一对方括号,所以我们需要计算第一个值是a11:
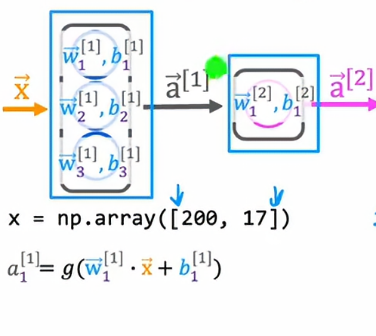
为了计算a11,我们有参数w11和b11,然后我们计算wx+b这个值,最后应用到sigmoid函数:
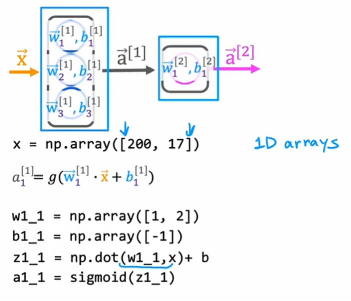
同理,a12,a13也是这个道理
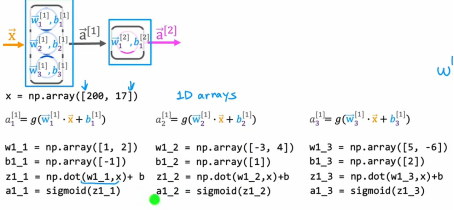
现在第一层的输出我们已经得到了,我们把其输入到第二层也就是输出层中,我们会有对应的w21和b21,然后我们计算z和输出a:
1、前向传播的一般实现
在上一节我们知道如何在Python中实现前向传播,但是需要为每个神经元逐行硬编码,现在我们来看在Python中更加通用的前向传播实现,我们需要做的是编写一个函数来实现一个密集层,也是神经网络的单层,所以我们要定义一个密集函数,它接受来自上一层的激活值,以及给这一层神经元的参数w和b
使用上一节的例子,如果第一层有三个神经元,那么如果w1和w2和w3是这些

那么我们会把所有这些权重向量堆叠成一个矩阵,这将是一个2X3的矩阵

第一列是w11,第二列是w12,第三列是w13,如果我们知道b,那么我们也可以将三个b堆叠成一个一维数组b,所有密集函数将接受来自上一层的激活值作为输入

这个dense函数要做的是接受a作为输入,然后输出来自当前层的激活值,这是代码

首先,是units = w.shape[1],因为w是一个2x3矩阵,w.shape[1]是说明这个矩阵有几列,所以units = 3,接下来我们将a设置为一个全零数组,元素数量与单元数量相同,所以在这个例子中,我们需要输出三个激活值,所以这里只是将a设置为全0 ,接下来我们通过一个for循环来计算第一个, w= W[:,j]这个代码是在Python中取出矩阵第j列的方法,所以第一次循环时,所以它会提取w11,当我们计算第二个单元的激活时,它会提取对应的第二列w12,第三次循环以此类推,然后我们用常用公式计算z即该参数w与我们已有的激活值之间的点积,我们就计算了激活向量a的所有三个值,然后最终返回a,那么dense函数的作用是输入来自上一层的激活值,并给定当前层的参数,它返回下一层的激活值。
因此给定dense函数,下面是如何通过顺序串联几个密集层来实现神经网络中的前向传播

给定输入特征x,然后我们就能用dense函数计算a1,然后再用a1取计算a3,以此类推,这样我们算到最后,也就是a4,就能得到我们需要的结果,最后返回该结果,也就是f_x,请注意,我们在dense中输入的Wn,是大写的W,也就是说,我们输入的是矩阵。
二、神经网络如何高效实现
深度学习研究人员能够扩展神经网络并构建非常大型网络的原因之一是因为神经网络可以矢量化,它们可以使用矩阵乘法非常高效地实现,事实证明并行计算硬件非常擅长进行非常大的矩阵乘法,在本节中,我们将了解这些矢量化神经网络的实现是如何工作的

这是我们在上面提到的前向传播的代码,事实证明,我们可以开发出一个向量化实现这个函数的方法,如下所示

将X设置为一个二维数组,W和B跟前面是一样的,np.matmul(A_in, W)是NumPy进行矩阵乘法的方式,两个矩阵相乘然后在加上一个B,等于激活函数,两种方法相比,肯定是向量在密集层的前向传播中更加高效
总结
通过咖啡烘焙模型中前向传播的学习,我们知道如何具体实现前向传播,并且理解了每一层中神经元的具体的运行过程,我还了解到,在选择激活函数的时候,不仅仅只有sigmoid函数,还有线性函数、Relu函数等,这些激活函数会在后面的学习中会有深刻的学习