C语言需要掌握的基础知识点之前缀和

傻童:CPU2025-10-24 0:06

C语言需要掌握的基础知识点之前缀和

前缀和（Prefix Sum）是一种重要的数据处理技术，它可以在预处理后快速计算数组任意区间的和。这种技术在算法竞赛和实际开发中都有广泛应用。

前缀和的基本概念

前缀和是一个数组，其中每个元素存储原数组从第一个元素到当前位置所有元素的和。

对于数组 arr[0...n-1]，其前缀和数组 prefix 定义为：

c 复制代码 
prefix[0] = arr[0]

prefix[i] = arr[0] + arr[1] + ... + arr[i]



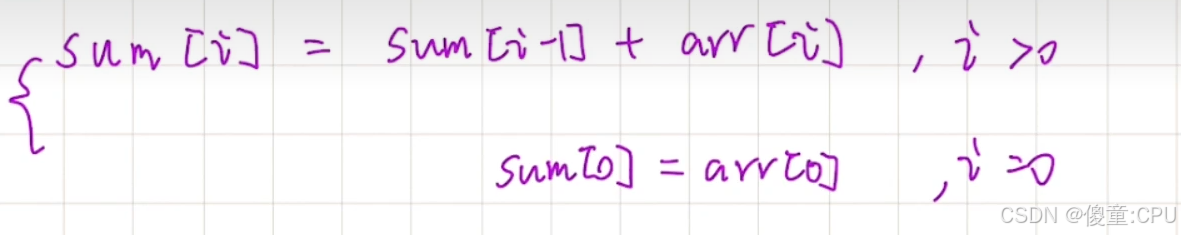
一维前缀和

基本实现

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 构建前缀和数组
void buildPrefixSum(int arr[], int n, int prefix[]) {
    prefix[0] = arr[0];
    for (int i = 1; i < n; i++) {
        prefix[i] = prefix[i - 1] + arr[i];
    }
}

// 计算区间 [l, r] 的和
int rangeSum(int prefix[], int l, int r) {
    if (l == 0) {
        return prefix[r];
    }
    return prefix[r] - prefix[l - 1];
}

int main() {
    int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    int n = sizeof(arr) / sizeof(arr[0]);
    
    int *prefix = (int*)malloc(n * sizeof(int));
    
    // 构建前缀和数组
    buildPrefixSum(arr, n, prefix);
    
    // 输出原数组
    printf("原数组: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    
    // 输出前缀和数组
    printf("前缀和: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", prefix[i]);
    }
    printf("\n");
    
    // 计算区间和
    printf("区间 [2, 5] 的和: %d\n", rangeSum(prefix, 2, 5));
    printf("区间 [0, 3] 的和: %d\n", rangeSum(prefix, 0, 3));
    printf("区间 [7, 9] 的和: %d\n", rangeSum(prefix, 7, 9));
    
    free(prefix);
    return 0;
}

优化版本（包含边界处理）

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 更通用的前缀和实现（从1开始索引，方便处理边界）
int* buildPrefixSumOptimized(int arr[], int n) {
    // 前缀和数组大小为 n+1，prefix[0] = 0
    int *prefix = (int*)malloc((n + 1) * sizeof(int));
    prefix[0] = 0;
    
    for (int i = 1; i <= n; i++) {
        prefix[i] = prefix[i - 1] + arr[i - 1];
    }
    return prefix;
}

// 计算区间 [l, r] 的和（0-indexed）
int rangeSumOptimized(int prefix[], int l, int r) {
    // prefix[r+1] - prefix[l] 得到区间 [l, r] 的和
    return prefix[r + 1] - prefix[l];
}

int main() {
    int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    int n = sizeof(arr) / sizeof(arr[0]);
    
    int *prefix = buildPrefixSumOptimized(arr, n);
    
    printf("前缀和数组 (包含前导0): ");
    for (int i = 0; i <= n; i++) {
        printf("%d ", prefix[i]);
    }
    printf("\n");
    
    // 测试多个区间和
    int testCases[][2] = {{0, 2}, {1, 4}, {3, 7}, {0, 9}};
    int numTests = sizeof(testCases) / sizeof(testCases[0]);
    
    for (int i = 0; i < numTests; i++) {
        int l = testCases[i][0];
        int r = testCases[i][1];
        int sum = rangeSumOptimized(prefix, l, r);
        printf("区间 [%d, %d] 的和: %d\n", l, r, sum);
    }
    
    free(prefix);
    return 0;
}

二维前缀和

基本概念

对于二维数组，前缀和可以快速计算任意子矩阵的和。

定义:二维前缀和是指从左上角(1，1)累加到(i，j)。



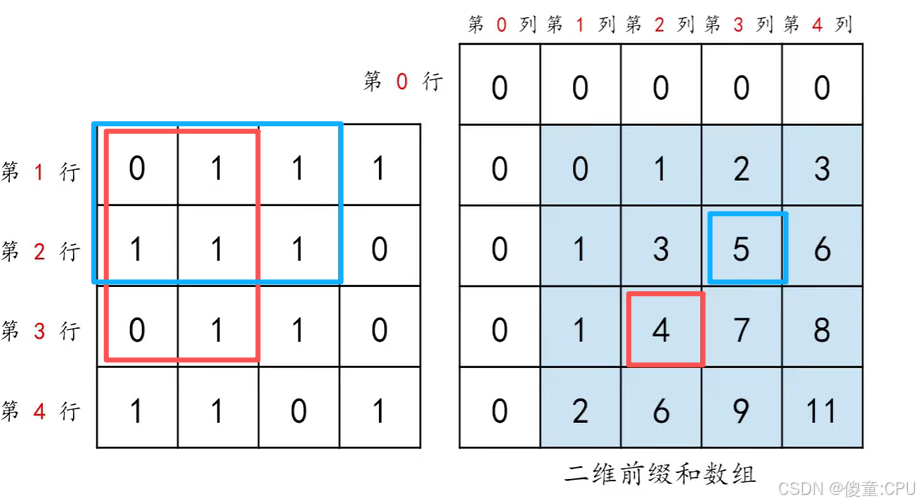
c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 构建二维前缀和数组
void build2DPrefixSum(int **matrix, int rows, int cols, int **prefix) {
    // 第一行
    prefix[0][0] = matrix[0][0];
    for (int j = 1; j < cols; j++) {
        prefix[0][j] = prefix[0][j - 1] + matrix[0][j];
    }
    
    // 第一列
    for (int i = 1; i < rows; i++) {
        prefix[i][0] = prefix[i - 1][0] + matrix[i][0];
    }
    
    // 其他位置
    for (int i = 1; i < rows; i++) {
        for (int j = 1; j < cols; j++) {
            prefix[i][j] = prefix[i - 1][j] + prefix[i][j - 1] 
                          - prefix[i - 1][j - 1] + matrix[i][j];
        }
    }
}

// 计算子矩阵和 [r1, c1] 到 [r2, c2]
int submatrixSum(int **prefix, int r1, int c1, int r2, int c2) {
    int total = prefix[r2][c2];
    int left = (c1 > 0) ? prefix[r2][c1 - 1] : 0;
    int top = (r1 > 0) ? prefix[r1 - 1][c2] : 0;
    int corner = (r1 > 0 && c1 > 0) ? prefix[r1 - 1][c1 - 1] : 0;
    
    return total - left - top + corner;
}

int main() {
    int rows = 4, cols = 4;
    
    // 创建并初始化矩阵
    int **matrix = (int**)malloc(rows * sizeof(int*));
    int **prefix = (int**)malloc(rows * sizeof(int*));
    
    for (int i = 0; i < rows; i++) {
        matrix[i] = (int*)malloc(cols * sizeof(int));
        prefix[i] = (int*)malloc(cols * sizeof(int));
    }
    
    // 填充测试数据
    int count = 1;
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            matrix[i][j] = count++;
        }
    }
    
    // 构建前缀和
    build2DPrefixSum(matrix, rows, cols, prefix);
    
    printf("原矩阵:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            printf("%2d ", matrix[i][j]);
        }
        printf("\n");
    }
    
    printf("\n前缀和矩阵:\n");
    for (int i = 0; i < rows; i++) {
        for (int j = 0; j < cols; j++) {
            printf("%2d ", prefix[i][j]);
        }
        printf("\n");
    }
    
    // 测试子矩阵和
    printf("\n子矩阵和测试:\n");
    printf("子矩阵 [1,1] 到 [2,2] 的和: %d\n", 
           submatrixSum(prefix, 1, 1, 2, 2));
    printf("子矩阵 [0,0] 到 [1,1] 的和: %d\n", 
           submatrixSum(prefix, 0, 0, 1, 1));
    printf("子矩阵 [0,1] 到 [2,3] 的和: %d\n", 
           submatrixSum(prefix, 0, 1, 2, 3));
    
    // 释放内存
    for (int i = 0; i < rows; i++) {
        free(matrix[i]);
        free(prefix[i]);
    }
    free(matrix);
    free(prefix);
    
    return 0;
}

前缀和的实际应用

  1. 统计区间频率
c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 使用前缀和统计某个值在区间内出现的次数
void frequencyInRange(int arr[], int n, int target) {
    // 创建频率前缀和数组
    int *freqPrefix = (int*)malloc((n + 1) * sizeof(int));
    freqPrefix[0] = 0;
    
    for (int i = 1; i <= n; i++) {
        freqPrefix[i] = freqPrefix[i - 1] + (arr[i - 1] == target ? 1 : 0);
    }
    
    printf("数组: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    
    printf("数字 %d 在各区间出现的次数:\n", target);
    int intervals[][2] = {{0, 2}, {1, 4}, {3, 7}, {0, 9}};
    int numIntervals = sizeof(intervals) / sizeof(intervals[0]);
    
    for (int i = 0; i < numIntervals; i++) {
        int l = intervals[i][0];
        int r = intervals[i][1];
        int count = freqPrefix[r + 1] - freqPrefix[l];
        printf("区间 [%d, %d]: %d 次\n", l, r, count);
    }
    
    free(freqPrefix);
}

int main() {
    int arr[] = {2, 3, 2, 2, 5, 2, 7, 2, 9, 2};
    int n = sizeof(arr) / sizeof(arr[0]);
    
    frequencyInRange(arr, n, 2);
    
    return 0;
}

解决子数组和问题

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 查找和为k的子数组个数
int subarraySum(int arr[], int n, int k) {
    // 构建前缀和数组
    int *prefix = (int*)malloc((n + 1) * sizeof(int));
    prefix[0] = 0;
    
    for (int i = 1; i <= n; i++) {
        prefix[i] = prefix[i - 1] + arr[i - 1];
    }
    
    int count = 0;
    
    // 查找所有满足 prefix[j] - prefix[i] == k 的区间
    for (int i = 0; i < n; i++) {
        for (int j = i; j < n; j++) {
            if (prefix[j + 1] - prefix[i] == k) {
                count++;
                printf("找到子数组 [%d, %d]: ", i, j);
                for (int x = i; x <= j; x++) {
                    printf("%d ", arr[x]);
                }
                printf("\n");
            }
        }
    }
    
    free(prefix);
    return count;
}

int main() {
    int arr[] = {1, 1, 1, 2, 2, 3};
    int n = sizeof(arr) / sizeof(arr[0]);
    int k = 3;
    
    printf("数组: ");
    for (int i = 0; i < n; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
    
    int result = subarraySum(arr, n, k);
    printf("和为 %d 的子数组个数: %d\n", k, result);
    
    return 0;
}

性能比较

c 复制代码 
#include <stdio.h>
#include <time.h>

// 传统方法：直接计算区间和
int directRangeSum(int arr[], int l, int r) {
    int sum = 0;
    for (int i = l; i <= r; i++) {
        sum += arr[i];
    }
    return sum;
}

// 前缀和方法
int prefixRangeSum(int prefix[], int l, int r) {
    return prefix[r + 1] - prefix[l];
}

int main() {
    const int n = 100000;
    int *arr = (int*)malloc(n * sizeof(int));
    int *prefix = (int*)malloc((n + 1) * sizeof(int));
    
    // 初始化数组
    for (int i = 0; i < n; i++) {
        arr[i] = i + 1;
    }
    
    // 构建前缀和
    prefix[0] = 0;
    for (int i = 1; i <= n; i++) {
        prefix[i] = prefix[i - 1] + arr[i - 1];
    }
    
    // 性能测试
    clock_t start, end;
    int queries = 10000;
    
    // 测试传统方法
    start = clock();
    long long sum1 = 0;
    for (int i = 0; i < queries; i++) {
        int l = i % (n - 100);
        int r = l + 100;
        sum1 += directRangeSum(arr, l, r);
    }
    end = clock();
    printf("传统方法时间: %f 秒\n", (double)(end - start) / CLOCKS_PER_SEC);
    
    // 测试前缀和方法
    start = clock();
    long long sum2 = 0;
    for (int i = 0; i < queries; i++) {
        int l = i % (n - 100);
        int r = l + 100;
        sum2 += prefixRangeSum(prefix, l, r);
    }
    end = clock();
    printf("前缀和方法时间: %f 秒\n", (double)(end - start) / CLOCKS_PER_SEC);
    
    printf("结果验证: %s\n", (sum1 == sum2) ? "正确" : "错误");
    
    free(arr);
    free(prefix);
    return 0;
}
相关推荐
degen_5 小时前
第一次进入 PEICORE 流程
c语言·笔记
爱吃山竹的大肚肚5 小时前
@Valid校验 -（Spring 默认不支持直接校验 List＜@Valid Entity＞，需用包装类或手动校验。）
java·开发语言
又见野草5 小时前
软件设计师知识点总结：数据结构与算法（超级详细）
数据结构·算法·排序算法
我是大咖5 小时前
C语言-贪吃蛇项目开发工具篇---ncursee库安装
c语言·开发语言
GalaxyPokemon5 小时前
有一个服务器，用于提供HTTP服务，但是需要限制每个用户在任意的100秒内只能请求60次，怎么实现这个功能
算法
雨夜之寂5 小时前
mcp java实战 第一章-第一节-MCP协议简介.md
java·后端
czy87874755 小时前
用C语言实现单例模式
c语言·单例模式
皮皮林5516 小时前
蚂蚁又开源了一个顶级 Java 项目！
java
fl1768316 小时前
基于opencv+Mediapipe+CNN实现用手势识别控制对鼠标操控python源码+项目说明+设计文档
算法
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08Labelme从安装到标注：零基础完整指南092025软件测试面试八股文（含答案+文档）10一文了解国产算子编程语言 TileLang，TileLang 对国产开源生态的影响与启示