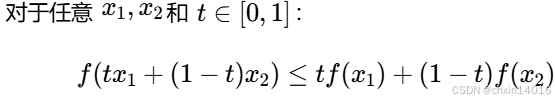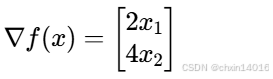优化算法——动手学深度学习11

chxin140162025-10-24 12:54

环境：PyCharm + python3.8

如（1.2. 深度学习中的优化挑战）中所说，

  • 本章关注：优化算法在 最小化目标函数方面的 性能，而非模型的泛化误差。

👉【优化算法】

主流优化算法及其特点
算法 核心思想 优势 局限性 适用场景
SGD 随机梯度下降，按固定学习率更新参数 简单，理论保证强 （凸函数收敛） 收敛慢，需手动调学习率 资源有限时 （如嵌入式设备）
Momentum 引入动量项，加速收敛并抑制震荡（） 缓解梯度震荡，加快平坦区域收敛 需调动量系数 β 图像分类、RNN等长序列任务
【AdaGrad 自调整学习率，对频繁参数缩小步长，对稀疏参数放大步长（η/Gt​​） 适合稀疏数据（如NLP） 长期累积导致学习率过早衰减 文本分类、推荐系统。
【RMSProp 改进AdaGrad，使用指数加权平均梯度平方 （​） 解决AdaGrad学习率 衰减过快问题 需调 β 和初始学习率 非平稳目标函数 （如强化学习）
【Adam 结合Momentum和RMSProp， 自适应调整一阶矩（动量） 和二阶矩（梯度平方） 自动调参，收敛快，鲁棒性强 可能收敛到次优解 （需调整 ϵ） 通用场景（CV、NLP、推荐等）
Nadam Adam + Nesterov动量， 提前预估梯度方向 进一步加速收敛 计算稍复杂 需快速收敛的复杂任务

1. 优化和深度学习

  • 对于深度学习 问题，通常会先定义损失函数。
  • 一旦有了损失函数，就可以使用优化算法 来尝试最小化损失。
  • 在优化中，
    • 损失函数 ：通常被称为优化问题的目标函数。
    • 按照传统惯例 ，大多数优化算法都关注的是最小化。
    • 若需要最大化目标 ：则 可在目标函数前加负号。

1.1. 优化的目标

本质上，优化和深度学习的目标是根本不同的：（核心目标差异）

  • 优化算法 的目标：
    • 最小化训练数据集上的损失函数 （即经验风险）
    • 关注的是模型在已知数据上的拟合能力
  • 深度学习 的目标：
    • 在有限数据下寻找泛化能力强的模型 ，即最小化整个数据分布的预期损失 （即风险）
    • 关注的是模型在未知数据上的表现

关键矛盾：

  • 训练误差（优化目标）≠ 泛化误差（深度学习目标）
  • 优化算法可能过度拟合训练数据，导致泛化能力下降（过拟合）

在 (多层感知机实现------ 动手学深度学习4.2~4.9_多层感知机开源代码-CSDN博客中的 模型选择、欠拟合和过拟合)中，详细讨论了这两个目标之间的区别。例如，

  • 训练误差和泛化误差通常不同：
    • 优化算法：
      • 目标函数通常是基于训练数据集的损失函数，
      • 因此优化的目标是减少训练误差。
    • 深度学习（或更广义地说，统计推断）：
      • 目标：减少泛化误差。
      • 具体实现：除了使用优化算法来减少训练误差之外，还需要注意过拟合。
python 复制代码 
import numpy as np
import torch
from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
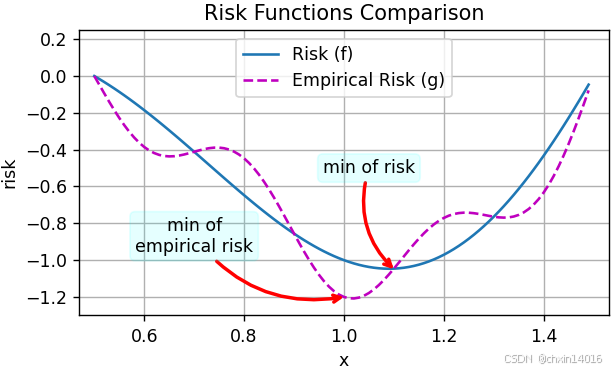
import common

为了说明上述不同的目标，引入两个概念风险 和经验风险 。如 (多层感知机实现------ 动手学深度学习4.2~4.9_多层感知机开源代码-CSDN博客中的 环境和分布偏移---3. 分布偏移纠正---3.1. 经验风险与实际风险) 所述，

  • 经验风险 ：是 训练数据集 的 平均损失 ，是风险的近似
    • (xi,yi) 训练样本，n 样本数量
    • 关键区别 ：是实际可计算的代理目标，但受限于有限数据，可能不平滑或存在噪声
  • 风险 ：是 整个数据群 的 预期损失 ，反映模型在未知数据上的平均表现
    • P 真实数据分布，L 损失函数，θ 模型参数
    • 关键区别 ：理论上的全局目标，但不可直接计算（需知道真实分布 P）

下面定义两个函数：

  • 风险函数 f
  • 经验风险函数 g

假设只有 有限的训练数据。因此，这里的g不如f平滑：

python 复制代码 
def f(x):
    '''风险函数
    理论风险值：x * cos(πx)
    理论风险的简化模拟：
        模拟真实数据分布下的期望损失
        cos(πx)项：反映损失随 参数x 的振荡变化
        全局最小值对应最优模型参数
    '''
    return x * torch.cos(np.pi * x)

def g(x):
    '''经验风险函数
    经验风险值 = 风险函数 + 高频噪声项
    f(x)：继承理论风险的基础形态
    0.2*cos(5πx)：模拟有限样本导致的波动
        振幅0.2：反映 数据量不足带来的估计误差
        高频5π ：反映 经验风险的局部波动性
    '''
    # 在风险函数基础上添加高频振荡项（模拟训练数据噪声）
    return f(x) + 0.2 * torch.cos(5 * np.pi * x)

下图说明，训练数据集的最低经验风险可能与最低风险（泛化误差）不同。

python 复制代码 
def annotate(text, xy, xytext, ax=None, fontsize=10, arrowprops=None):
    '''在图中添加带箭头的注释（增强版）
    text        : 注释文本
    xy          : 被注释点坐标 (x,y)
    xytext      : 文本位置坐标 (x,y)
    ax          : 目标坐标轴对象，默认为当前轴
    fontsize    : 文本字体大小
    arrowprops  : 箭头属性字典
    '''
    if arrowprops is None: # 默认箭头样式设置
        # 箭头样式，线宽，颜色
        arrowprops = dict(arrowstyle='->', linewidth=2, color='red',
                          shrinkA=0, # 箭头起点不收缩
                          shrinkB=0, # 箭头终点不收缩
                          connectionstyle="arc3,rad=0.3") # 带弧度的连接线
    ax = ax or plt.gca() # 获取或创建坐标轴对象

    # 坐标安全保护：确保注释点不超出图形范围
    xlim = ax.get_xlim() # 获取x轴范围
    ylim = ax.get_ylim() # 获取y轴范围
    xy = (np.clip(xy[0], *xlim), np.clip(xy[1], *ylim)) # 裁剪被注释点坐标
    xytext = (np.clip(xytext[0], *xlim), np.clip(xytext[1], *ylim)) # 裁剪文本位置坐标

    # 添加注释到图形，bbpx注释文本的背景框
    ax.annotate(text, xy=xy, xytext=xytext,
                fontsize=fontsize,
                ha='center', va='center',   # 水平居中，垂直居中
                arrowprops=arrowprops,      # 箭头样式
                bbox=dict(boxstyle="round", # 圆角边框
                          alpha=0.1,        # 背景透明度
                          color="cyan"))    # 背景颜色
python 复制代码 
# 绘制对比图：风险函数 & 经验风险函数
x = torch.arange(0.5, 1.5, 0.01) # 参数搜索范围
fig1, ax1 = common.plot(x, [f(x), g(x)], 'x', 'risk',
                        legend=['Risk (f)', 'Empirical Risk (g)'], # 添加图例
                        xlim=(0.47, 1.53), ylim=(-1.3, 0.25),
                        figsize=(6, 4), title='Risk Functions Comparison',
                        show_internally = False)
# 添加关键点注释
common.annotate('min of\nempirical risk',  (1.0, -1.2), (0.7, -0.87), ax=ax1) # 经验风险最小值点
common.annotate('min of risk', (1.1, -1.05), (1.05, -0.5), ax=ax1,) # 理论风险最小值点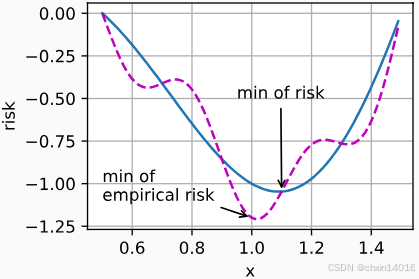

1.2. 深度学习中的优化挑战

  • 本章关注：优化算法在 最小化目标函数方面的 性能，而非模型的泛化误差。
  • 在 (机器学习 理论相关 (自用笔记)-CSDN博客中的 线性回归)中，区分了优化问题中的解析解和数值解。
  • 深度学习中，大多数目标函数都没有解析解。
  • 相反，我们必须使用数值优化算法。本章中的优化算法都属于此类别。

深度学习优化存在许多挑战。其中最令人烦恼的是：

  • 局部最小值
  • 鞍点
  • 梯度消失

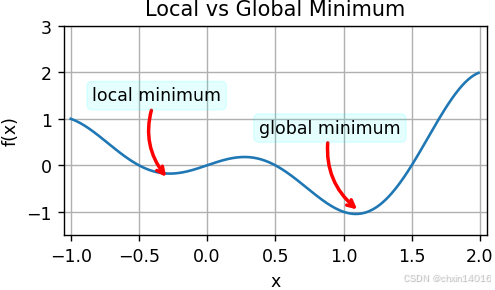
1.2.1. 局部最小值

对于任何目标函数 f(x)，若在 x 处对应的 f(x) 值

  • 小于 在 x 附近任意其他点的 f(x) 值 ===》 f(x) 可能是 局部最小值
  • 是 整个域中目标函数的最小值 ===》 f(x) 是 全局最小值

例如，给定函数（即 代码中，前面对比两种风险时的 风险函数 f(x)）

我们可以近似该函数的局部最小值和全局最小值。

python 复制代码 
# 绘制对比图：局部最小值 & 全局最小值
x = torch.arange(-1.0, 2.0, 0.01)
# 使用前面的风险函数 f(x)，对比两种风险时范围是0.5~1.5，现在看最小值的范围的-1.0~2.0
fig2, ax2 = common.plot(x, [f(x), ], 'x', 'f(x)',
                        xlim=(-1.05, 2.05), ylim=(-1.5, 3),
                        title='Local vs Global Minimum',
                        show_internally = False)
common.annotate('local minimum', (-0.3, -0.25), (-0.37, 1.5), ax=ax2)
common.annotate('global minimum', (1.1, -0.95), (0.9, 0.8), ax=ax2)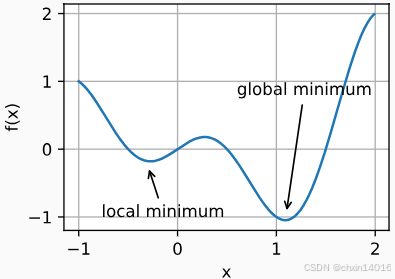

  • 深度学习模型的目标函数通常有许多局部最优解。
  • 当优化问题的数值解接近局部最优 值时 ，随着目标函数解的梯度接近或变为零 ，通过最终迭代获得的数值解可能仅 使目标函数 局部最优 ，而非 全局最优。
  • 一定 程度的噪声可 使参数跳出局部最小值。
    • 小批量随机梯度下降中，小批量上 梯度的自然变化 能助参数跳出局部极小值。

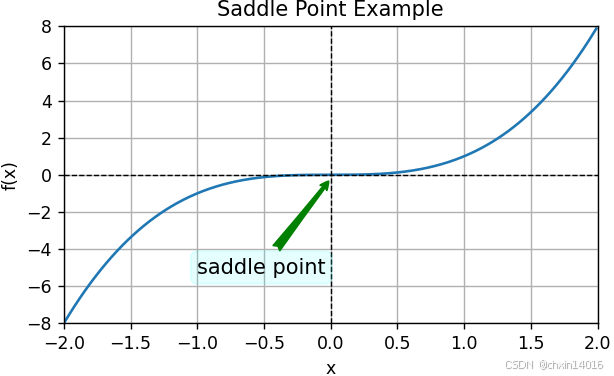
1.2.2. 鞍点

  • 除了局部最小值之外，鞍点是梯度消失的另一个原因。
  • 鞍点 （saddle point）：
    • 指 函数的所有梯度都消失，
    • 但既不是全局最小值，也不是局部最小值 的任何位置。

例如，函数 ：

  • 它的一阶和二阶导数在 x=0 时消失。
  • 这时优化可能会停止，但此处并非最小值。
python 复制代码 
# 绘制鞍点示例图
x = torch.arange(-2.0, 2.0, 0.01) # 扩展参数范围
fig3, ax3 = common.plot(x, [x**3], 'x', 'f(x)',
                      xlim=(-2, 2), ylim=(-8, 8),
                      figsize=(6, 4), title='Saddle Point Example',
                        show_internally = False)
common.annotate('saddle point', (0, -0.2), (-0.52, -5.0),
                ax = ax3, fontsize = 12,
                arrowprops = dict(arrowstyle='fancy', color='green')) # 鞍点注释
# 添加参考线
plt.axhline(y=0, color='k', linestyle='--', linewidth=0.8)  # 添加x轴虚线
plt.axvline(x=0, color='k', linestyle='--', linewidth=0.8)  # 添加y轴虚线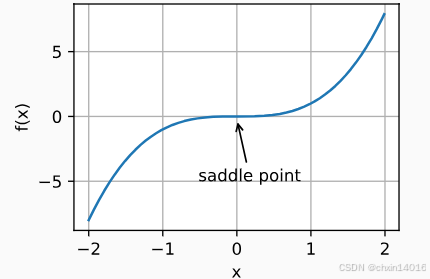

如下例所示，较高维度的鞍点甚至更加隐蔽。

  • 例如， 是典型的鞍点函数：
    • 其鞍点为 (0,0)，在(0,0)处梯度为0（一阶导数为2x和-2y）
      • 这是关于 y 的最大值，
      • 也是关于 x 的最小值。
    • Hessian矩阵为[[2,0],[0,-2]]，特征值一正一负，符合鞍点定义
    • 此外，它看起来像个马鞍，即 鞍点的名字由来。
python 复制代码 
# 创建二维网格：在[-1,1]区间生成101x101的网格点坐标矩阵
# torch.linspace创建等差数列，torch.meshgrid将一维坐标扩展为二维网格
x, y = torch.meshgrid(
    torch.linspace(-1.0, 1.0, 101),  # x坐标范围[-1,1]，101个点
    torch.linspace(-1.0, 1.0, 101))   # y坐标范围[-1,1]，101个点

# 定义鞍点函数：z = x² - y²
# 该函数在(0,0)处Hessian矩阵特征值为(2, -2)，是典型的鞍点
z = x**2 - y**2

ax = plt.figure().add_subplot(111, projection='3d') # 创建三维坐标轴对象

# 绘制三维线框图
# plot_wireframe以线框形式绘制曲面
# 通过rstride/cstride控制行/列方向的网格密度（步长）
ax.plot_wireframe(x, y, z, **{'rstride': 10, 'cstride': 10})

# 红色叉号标记鞍点位置(0,0,0)，直观展示梯度消失点
ax.plot([0], [0], [0], 'rx') # 第一个列表表示x坐标，第二个y坐标，第三个z坐标

# 设置坐标轴刻度
ticks = [-1, 0, 1]      # 统一设置刻度为[-1,0,1]
plt.xticks(ticks)       # 设置x轴刻度
plt.yticks(ticks)       # 设置y轴刻度
ax.set_zticks(ticks)    # 设置z轴刻度

# 添加坐标轴标签
plt.xlabel('x')
plt.ylabel('y')
ax.set_zlabel('z')  # 补充z轴标签
# plt.savefig('saddle_point.png', dpi=300, bbox_inches='tight') # 保存图像到文件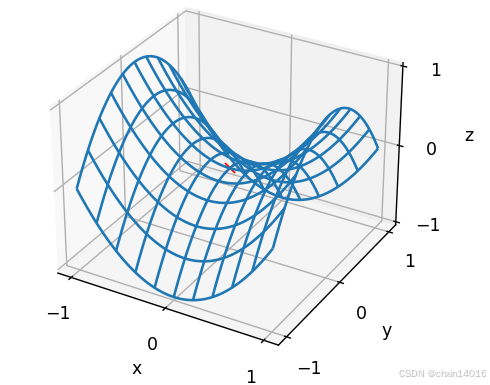

函数与Hessian矩阵特性 ：假设函数的输入是 k维向量，其输出是标量，因此其Hessian矩阵（也称黑塞矩阵）将有 k个特征值（参考特征分解的在线附录)。函数的解可能是局部最小值、局部最大值 或 函数梯度为零位置处的鞍点：

  • 当函数在零梯度位置处的Hessian矩阵的特征值：
    • 全为正值 时，我们有该函数的 局部最小值
    • 全为负值 时，我们有该函数的 局部最大值
    • 为负值和正值 时，我们有该函数的一个 鞍点

高维度下鞍点与局部最小值情况：

  • 在高维度问题 中，至少部分特征值为负的可能性相当高。
  • 导致鞍点比局部最小值更易出现。

凸函数情况：

  • 凸函数是Hessian矩阵特征值永远不为负值的函数。
  • 是研究优化算法的良好工具。
  • 但 大多数深度学习问题并不属于这一类。

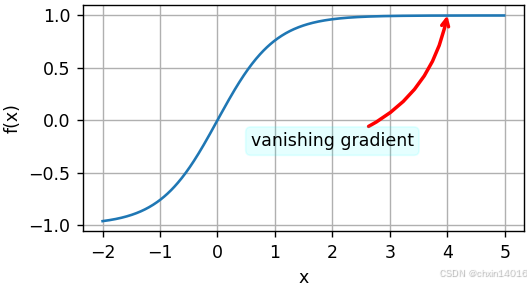
1.2.3. 梯度消失

梯度消失的核心问题：

  • 定义：
    • 在DNN的反向传播过程中，
    • 梯度（即导数）通过链式法则 从输出层向输入层 逐层传递时，
    • 若每一层的梯度都小于1（如Sigmoid/Tanh的饱和区），经过多层累积后，
    • 其​幅度（绝对值）会急剧减小（指数级衰减）​，以至于接近零。
  • 后果：
    • 靠近输入层的参数更新几乎停滞（权重几乎无法更新），
    • 模型无法有效学习深层特征，导致训练失败或收敛极慢。

典型场景示例：

  • 回想一下在（机器学习 理论相关 (自用笔记)-CSDN博客中 神经网络：多层感知机 的 2. 激活函数）中常用的激活函数及其衍生函数。
  • 例如，
    • 假设想要最小化函数 ，又恰好从 x=4 开始。
    • 则 的梯度接近零。
    • 更具体地说， ，所以 。
    • 因此，在取得进展前，优化会停滞很长一段时间。
    • 而实际上，在引入ReLU激活函数之前，这就是训练深度学习模型相当棘手的原因之一。
python 复制代码 
x = torch.arange(-2.0, 5.0, 0.01)
fig4, ax4 = common.plot(x, [torch.tanh(x)], 'x', 'f(x)', show_internally=False)
common.annotate('vanishing gradient', (4, 1), (2, -0.20), ax=ax4)

  • 无需全局最优 ：局部最优解 或 近似解通常已足够好。
    • （如分类任务中，局部最优的准确率可能接近全局最优）
  • 高维空间的局部最优性质：在高维空间中，鞍点比严格的局部最优解更常见，现代算法（如Adam）可通过扰动逃离。
  • 近似解的实用性：局部最优解的损失值可能仅比全局最优高0.1%，但实际性能差异极小。
  • 经验证据 ：实验表明，随机初始化的多次训练可能收敛到不同局部最优，但测试性能接近。
    • 例如，ResNet在ImageNet上的不同随机种子训练，Top-1准确率波动通常<0.5%。

小结

  • 最小化训练误差并不能保证我们找到最佳的参数集来最小化泛化误差。

  • 优化问题可能有许多局部最小值。

  • 一个问题可能有很多的鞍点，因为问题通常不是凸的。

  • 梯度消失可能会导致优化停滞，

    • 重参数化通常会有所帮助。

    • 对参数进行良好的初始化也可能是有益的。

2. 凸性

2.1. 定义

  • 凸集 （convex sets）：集合内 任意两点之间连线 的整条线段 皆包含在该集合内 。
    • 交集保持凸性​ ：凸集的交集 是凸的
    • 并集不保持凸性​ ：凸集的并集不一定 是凸的
  • 凸函数 （convex functions）：函数值 ≤ 弦的值（弦在函数上方，即 线段在图像上方） 。
    • 凸函数的局部极小值也是全局极小值
    • 凸函数的下水平集是凸的（碗形山谷的所有海拔低于100米的区域，肯定是一片连起来的、中间没有空洞的洼地）
    • 判断函数是否 "凸" ：如果凸的话→二阶导≥0 / 半正定
      • 一维 ，一元函数 f(x)："加速度" 二阶导数 f''(x) 必须永远 >= 0
      • 多维 ，多元函数 f(x, y, z...)： 其 ​​Hessian 矩阵 （即 包含所有方向"加速度"的矩阵）是否 半正定 (H ⪰ 0)
        • 半正定：
          • 用于描述 "只升不降" 的性质
          • 一个多元函数是凸的，当且仅当，把它任意"切片"后，得到的一元函数，也都是凸的。

2.1.1. 凸集

凸集（convex set）是凸性的基础。简单地说，

  • 若对于任何 ，连接 a 和 b 的线段也位于 中，则向量空间中的一个集合 是凸（convex）的。
  • 在数学术语上，这意味着对于所有 ，我们得到

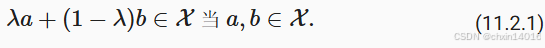凸集的正式定义

这听起来有点抽象，那我们来看一下 图11.2.1里的例子。

  • 第一组存在不包含在集合内部的线段，所以该集合是非凸的。
  • 而另外两组则没有该问题。

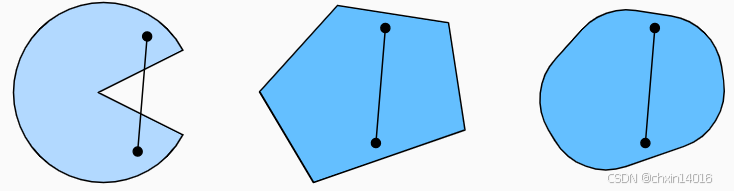图11.2.1 第一组是非凸的，另外两组是凸的

接下来来看一下交集 图11.2.2。

  • 假设 和 是凸集，则 也是凸集的。
  • 现在考虑任意 ， 因为 和 是凸集，所以连接 a 和 b 的线段包含在 和 中。
  • 鉴于此，它们也需要包含在 中，从而证明我们的定理。

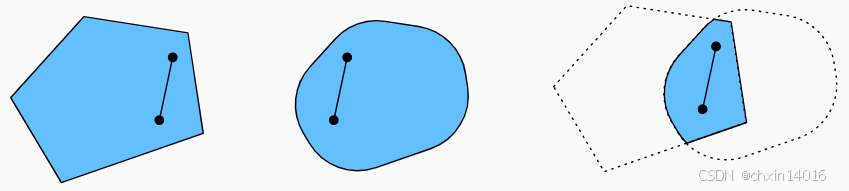图11.2.2 两个凸集的交集是凸的

我们可以毫不费力地进一步得到这样的结果：

  • 给定凸集 ，它们的交集 是凸的。
  • 但是反向是不正确的，考虑两个不相交的集合 ，取 和 。
    • （ ​ 即 ∅​ ：空集 (Empty Set)，一个​不包含任何元素​的集合）
    • 因为假设 ，在 图11.2.3中连接 a 和 b 的线段需包含一部分既不在 也不在 中(红色部分)。
    • 红色线段不包含在并集 中，因此证明了凸集的并集不一定是凸的，即非凸（nonconvex）的。

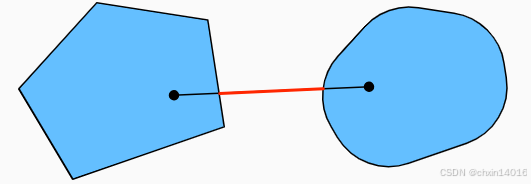图11.2.3 两个凸集的并集不一定是凸的

深度学习中大部分优化问题在凸集上进行。例如，

  • （常见凸集）（深度学习中​两种常见的优化"舞台"）
  • 例子1：整个空间
    • = 所有可能的d维向量组成的空间。比如
      • ℝ²：整个平面
      • ℝ³：整个三维空间
    • 即实数的 d-维向量的集合是凸集 (毕竟 中任意两点之间的线存在 )中。
    • 在深度学习中应用：当​没有约束​时，参数可以在所有实数范围内自由取值。
  • 例子2：球约束（有界约束）​
    • 在某些情况下，我们使用有界长度的变量，例如球的半径定义为 且 。
      • = "所有长度不超过r的向量的集合"
      • = 向量x的长度（就像点到原点的距离）
      • r = 球的半径
    • 具体例子：

2.1.2. 凸函数

现在有了凸集，可以引入凸函数 （convex function） ：

  • 给定一个凸集 ，若对于所有 和 所有 ，函数 是凸的，
  • 则可以得到

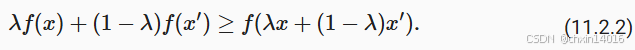
公式的直观解释​​：

  • 左边 ：在x₁和x₂之间的某个点（比如中点）的函数值
  • 右边 ：连接f(x₁)和f(x₂)的线段在该点的值
  • ≤ 表示 ：函数值 ≤ 弦的值（弦在函数上方）

具体例子说明​：

为了说明这一点，下面绘制一些函数并检查哪些函数满足要求。

  • 定义一些函数，包括凸函数和非凸函数：
python 复制代码 
# 定义三个函数
f = lambda x: 0.5 * x**2            # 凸函数  （典型，开口向上的抛物线）
g = lambda x: torch.cos(np.pi * x)  # 非凸函数（余弦波）
h = lambda x: torch.exp(0.5 * x)    # 凸函数  （指数增长）

# 生成数据
x = torch.arange(-2, 2, 0.01)
segment = torch.tensor([-1.5, 1]) # 用于绘制线段的两个端点

# d2l.use_svg_display()
_, axes = plt.subplots(1, 3, figsize=(9, 3))

for ax, func, name in zip(axes, [f, g, h],
                          ['f(x) = 0.5x²', 'g(x) = cos(πx)', 'h(x) = exp(0.5x)']):
    _, ax = common.plot([x, segment], [func(x), func(segment)], axes=ax,
                        title = name, show_internally=False)

plt.tight_layout() # 自动调整子图参数，以避免标签、标题等元素重叠或溢出
plt.show()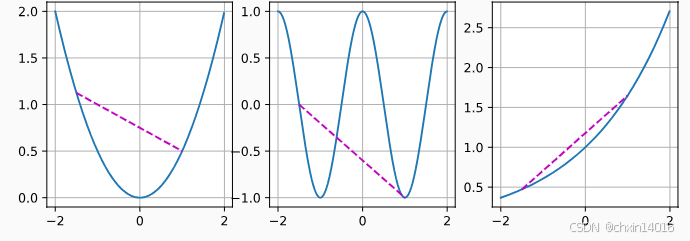

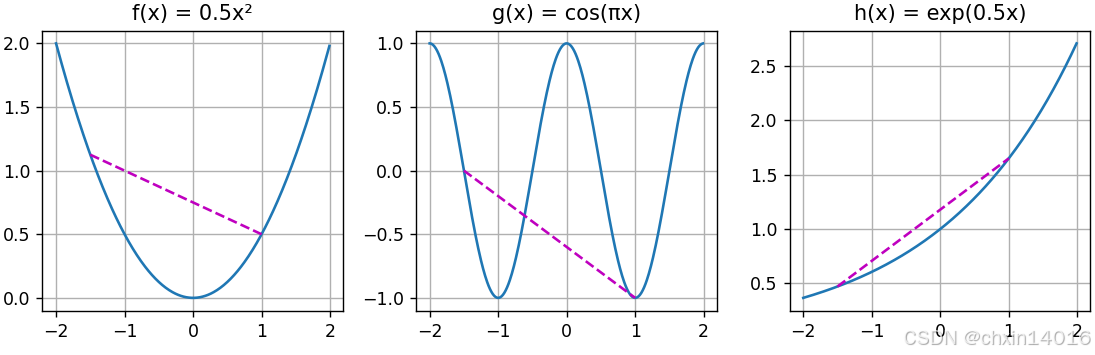
如图所示，

  • 余弦函数 → 非凸
  • 抛物线函数 和 指数函数 → 凸
  • 前提条件：定义域 必须是凸集。
    • 否则可能无法很好地界定 的结果。

2.1.3. 詹森不等式（描述凸函数特性）

詹森不等式(Jensen's inequality)：

  • 对于个凸函数 ，函数的平均值​不会小于​ 平均值的函数。即
    • 函数的平均值 ≥ 平均的函数值
    • 最终得到的结果值（放大器结合分蛋糕）：
      • 先放大后分 ≥ 先分后放大
      • 函数→放大器(假设为计算平方)，分蛋糕→平均
    • 通俗理解 1​ ：若先平均再计算函数值，得到的结果会比先计算函数值再平均​要小​（对于凸函数而言）。
    • 通俗理解 2​ ：​ 对于凸函数，先算平均再映射的结果，不会比先映射再算平均的结果更好。
      • 也就是 f(平均) <= 平均(f)，即 f(E[X]) <= E[f(X)]。
  • 它是凸性定义的一种推广：

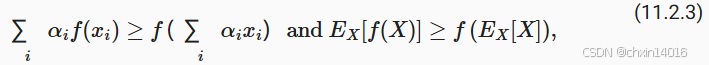
其中

  • ：满足 的非负实数
  • ：随机变量
  • 换句话说，凸函数的期望不小于期望的凸函数，其中后者通常是一个更简单的表达式。
  • 为了证明第一个不等式，我们多次将凸性的定义应用于一次求和中的一项。

詹森不等式的一个常见应用 ：用 一个较简单的表达式约束 一个较复杂的表达式。

  • 核心目的：​
    • 当我们无法直接计算一个复杂的目标（比如 P(X)）时，
    • 可以利用詹森不等式找到一个更简单的、可以计算的下界来替代它进行优化。
  • 例如，它可以应用于部分观察到的随机变量的对数似然。
  • 具体地说，由于 ，所以
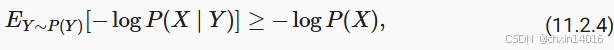
  • X：原始数据（要找模型的基础数据，即 指纹脚印等）
  • Y ：典型的未观察到的随机变量（永远看不到的"隐藏角色"Y​）
  • P(Y) ：它可能如何分布的最佳猜测（对凶手身份的"先验猜测"）
  • P(X) ：将 Y 积分后的分布
  • P(X | Y) ：若凶手是某个特定的人，他留下这些证据的可能性"
    • （比如，如果是惯犯A，他留下这种脚印的概率有多高）
  • 例如，在聚类中 Y 可能是簇标签，而在应用簇标签时， 是生成模型。
  • 核心难题：​ 你真正想知道的是 P(X)（即综合所有可能的凶手后，出现这些证据的总概率），但直接计算它需要把所有可能的凶手都考虑一遍，这非常困难。
  • 公式 说的就是这件事：
    • ​总的证据概率 P(X)，等于对每一个可能的凶手 Y，计算"他是凶手的概率" × "他留下证据的概率"，然后把所有结果加起来。

2.2. 性质

看一下凸函数一些有趣的性质。

2.2.1. 局部极小值是全局极小值

凸函数的局部极小值也是全局极小值。下面用反证法给出证明。

  • 假设 是一个局部最小值，则存在一个很小的正值 p ，使得当 满足 时，有 。
  • 现在假设局部极小值 不是 的全局极小值：存在 使得 。
  • 则存在 ，比如 ，使得 。

然而，根据凸性的性质，有

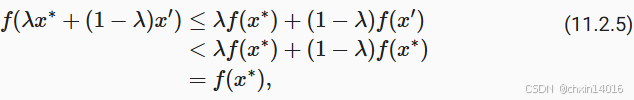
这与 是局部最小值相矛盾。因此，不存在 满足 。 综上所述，局部最小值 也是全局最小值。

例如，对于凸函数 ，有一个局部最小值 x = 1，它也是全局最小值。

python 复制代码 
f = lambda x: (x - 1) ** 2
common.plot([x, segment], [f(x), f(segment)], 'x', 'f(x)')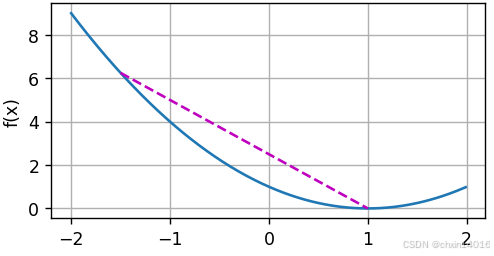
  • 凸函数的局部极小值同时也是全局极小值这一性质，意味着：只要最小化函数，就不会"卡住"。
  • 但注意，可能会存在以下两种情况：
    • ① 有多个全局最小值
      • 函数 在 [-1, 1] 区间上都是最小值。
    • ② 不存在一个全局最小值
      • 函数 在 上没有取得最小值。
        • 对于 ，它趋近于 0，但是没有 f(x)=0 的 x 。

2.2.2. 凸函数的下水平集是凸的

  • 下水平集： ，所有让函数值 f(x)小于等于某个标准 b的点 x构成的集合。
    • 例子​ ：f(x)是海拔高度，b=100米。那么 S_100就是所有海拔不超过100米的区域。

我们可以方便地通过凸函数的下水平集 （below sets）定义凸集。 具体来说，给定一个定义在凸集 上的凸函数 ，其任意一个下水平集

是凸的。可以快速证明一下：

  • 对于任何 （在下水平集里取两点）
  • 我们需要证明：当时 ， （在两点间任意取一点，假设是z）
  • 因为 且 （两点海拔皆低于100）
  • 所以
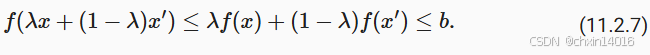
  • 解释下公式：
    • f(z) = f(λx + (1-λ)x')（点z的海拔）
    • <= λf(x) + (1-λ)f(x')（连接点x和点x'的线段在海平面上的投影高度）
    • 直接带入前面区间的两点 ，可计算出结果也是 <= b，证明结束。

2.2.3. 凸性和二阶导数（判断函数是否凸的方法）

快速判断一个函数是否凸：其二阶导数(黑塞矩阵)是否 半正定。

主要思想：

  • 把一个复杂的高维问题，转化为一系列简单的一维问题来解决。

基本策略：（如果凸的话→二阶导≥0 / 半正定）

  • ​一维情况（简单）：​ 对于一元函数 f(x)，判断凸性很简单：
    • ​它的"加速度"（二阶导数 f''(x)）必须永远 >= 0​。
    • 这意味着函数不能"向下弯"，只能"向上弯"或保持直线。
  • 多维情况（复杂）：​ 对于多元函数 f(x, y, z...)，判断凸性要看它的 ​Hessian 矩阵​ （可以理解为包含所有方向"加速度"的矩阵）是否 ​半正定​ (H ⪰ 0)。
    • 半正定：
      • 用于描述 "只升不降" 的性质
      • 一个多元函数是凸的，当且仅当，把它任意"切片"后，得到的一元函数，也都是凸的。

  • 目标：​ ​ 告诉大家，我们最终要证明 ​​"多元函数f是凸的 ⇔ 它的Hessian矩阵H是半正定的"​​。

  • ​​内容：​​

    • ​​开头：​ ​ 直接给出了最实用的结论：要检查凸性，就去算 Hessian 矩阵 H，然后看它是否半正定 (H ⪰ 0)。比如 f(x) = 1/2 * ||x||²是凸的，因为它的 H是单位阵，显然是半正定的。

    • ​​中间：​ ​ 给出了更正式的定义：​​f是凸的 ⇔ 它的所有"一维切片"g(z)是凸的​​。这是连接一维和多维的关键桥梁！

    • ​​最后：​ ​ 先证明一维情况为什么 f''(x) ≥ 0意味着凸性。它用一个非常巧妙的数学式子（11.2.8）和极限定义，直接推导出了二阶导数必须非负。

证明一维情况的另一面，并定义"切片函数"​​

  • ​​目标：​​ 补完一维情况的证明，并正式定义连接一维和多维的"桥梁函数"。

  • ​​内容：​​

    • ​​上半部分：​ ​ 证明了 f''(x) ≥ 0如何直接推导出凸函数的定义式。它利用了导数单调递增的性质和中值定理，通过代数推导，最终得到了凸函数的定义式 λf(b) + (1-λ)f(a) ≥ f(λa + (1-λ)b)。​​（这部分是严格的数学证明，如果觉得难，可以跳过，只需记住"二阶导非负 => 凸"这个结论就行）​​

    • ​​下半部分：​ ​ 提出了最重要的​​引理​ ​（桥梁）：要判断多元函数 f的凸性，可以看由它定义的的一维函数 g(z) = f(zx + (1-z)y)是否是凸的。​​这其实就是对"任意切片"的数学定义。​

利用"切片函数"完成最终证明​​

  • ​​目标：​​ 利用前两张图的结论，最终证明核心命题。

  • ​​内容：​​

    • ​​第一部分：​ ​ 证明了这个"桥梁"是双向的。即，如果多元函数 f是凸的，那么它的任意"切片" g(z)也是凸的。

    • ​​第二部分：​​ 完成了最终的逻辑链条：

      1. ​​已知：​ ​ 一维时，g(z)是凸的 ⇔ g''(z) ≥ 0。

      2. ​​计算：​ ​ 对 g(z) = f(zx + (1-z)y)求二阶导数，发现 g''(z) = (x-y)ᵀ H (x-y)。

      3. ​​连接：​ ​ 因此，g(z)是凸的 ⇔ (x-y)ᵀ H (x-y) ≥ 0对于所有x, y都成立。

      4. ​​结论：​ ​ 而这正是 ​​Hessian矩阵 H是半正定矩阵​​ 的定义

2.3. 约束

  • 凸优化的一个很好的特性：能够让我们有效地处理约束（constraints）。
  • 即它使我们能够解决以下形式的约束优化（constrained optimization）问题：
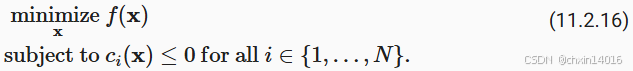
  • ：目标函数
  • ：约束函数
  • 目标：​ minimize f(x)-> 目标是​让某个东西最少​
    • （如"让总路程最短"或"让过路费最便宜"）
  • 限制条件：​ c_i(x) ≤ 0-> 你有一堆​必须遵守的规矩​
  • 则 优化问题就是：​在遵守所有规矩的前提下，最好地完成目标。

例如

  • 第一个约束 ，则参数 被限制为单位球
    • ||x||₂是向量 x的模长，即 ​"当前位置到坐标原点的距离"
    • ∴ ||x||₂ - 1 ≤ 0就意味着 ||x||₂ ≤ 1
    • 人话：整个行程路线，必须完全包含在一个以家(原点)为中心、半径为1公里的圆形区域内。不能跑到离家超过1公里以外的地方去
  • 第二个约束 ，那么这对应于半空间上所有的
    • 描述的是​一条直线的一侧​ （二维情况下）。v是直线的法向量，决定方向，b是偏移量
    • 人话：比如，规定"行程不能进入城市的北区"。​ 这条无形的界限就是那条直线，而"北区"就是被禁止的半空间。
  • 同时满足这两个约束等于选择一个球的切片作为约束集

2.3.1. 拉格朗日函数 (综合考量函数)（解决​​约束优化问题​​）

  • 目标函数的梯度 将被 约束函数的梯度 所抵消
    • ​"目标函数的梯度"​ = 重力的方向（球想往哪儿滚）
    • ​"约束函数的梯度"​ = 墙壁推力的方向（墙壁阻止球往某个方向滚）
    • ​"抵消"​ = 二力平衡，球不动了，达到平衡状态
  • 这个平衡点，就是带约束条件下的最低点。也就是鞍点。
  • 拉格朗日函数 的鞍点 是原始约束优化问题 的最优解。

就是爬山：

  • 约束是要走规定的山路（约束条件）
  • 我只想最短路径到达山顶（优化目标），所以选择直接走直线
  • 监督员就是拉格朗日乘子：过程中一直在把我往规定的山路上拉
    • 我偏得越严重，监督员就拉的程度越大
      • （c(x) > 0（严重偏离约束）时，需要大的 α来惩罚）
    • 我越没那么偏，监督员就拉的程度越小
      • （当 c(x)接近 0 但还未完全满足时，α会是一个适当的正值）
    • 最后达到平衡（找到拉格朗日函数 L的​鞍点）

若发现山路就是最佳路径，我自愿走找路上，无偏离倾向时：

  • 就是："对于 c_i(x) < 0中任意 x，我们最终会选择 α_i = 0" 。
  • 即 "监督员"就会完全消失（α=0）
    • 因为我已经自觉遵守了规则，他无需施加任何拉力。

假设

  • 目标 ：把一个球放地上，让它​处在最低的位置​（即 "优化目标"：最小化重力势能）
  • ​约束条件​ ：这个球​ 必须被关在盒子里​
  • 所以任务变成了：​​在这个盒子范围内，找到能让球停留的最低点
  • 效果：球会滚到最低的地方，重力将与盒子两侧对球施加的力平衡。
    • 即 重力与盒子内壁施加的力 相抵消。
    • 目标函数：重力
    • 约束函数：盒子内壁推回的力
    • ∴ 也可以解释为：目标函数(重力)的梯度 将被 约束函数的梯度 所抵消(由于墙壁的"推回"作用，需要保持在盒子内)。

注意：任何不起作用的约束（即球停在中间没接触壁）都将无法对球施加任何力。

  • 翻译成数学 ：若最优解离约束边界还很远（即 c(x) < 0），则该约束就是"不起作用的"。此时，对应的拉格朗日乘子 α = 0（因为不需要力）
  • 这被称为​互补松弛条件​ ：
    • 要么约束生效 ( ，且 α > 0)
    • 要么约束不起作用 ( ，且 α = 0)

这里我们简略拉格朗日函数 的推导，上述推理可以通过以下鞍点优化问题来表示：

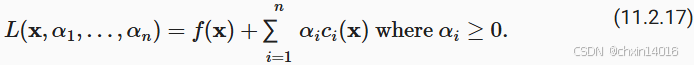
拉格朗日乘数 (Lagrange multipliers)：（作用：确保约束被正确地执行）

  • 公式中的变量 （），代表约束力度。
  • 选择它们的大小足以确保所有 的 。 例如，
    • 对于 (最优解离约束边界还很远)中任意 ，最终会选择 (约束不起任何作用)
    • 就是：发现山路就是最佳路径，我自愿走找路上，无偏离倾向的情况。
  • 此外，这是一个鞍点 （saddlepoint）优化问题：想要使 同时满足以下两点
    • 相对于 最大化 （maximize）（ 代表约束力度）
    • 相对于 最小化 （minimize）（即最小化 f(x)）
  • 有大量的文献解释如何得出函数。这里只需知道 的鞍点 是原始约束优化问题 的最优解就足矣。

简单的例子：

2.3.2. 惩罚 (往回拉)（解决优化约束问题时的作弊技巧）

解决水龙头流速问题：

  • 精确思路（硬约束）：要流速精准恰好
    • 需精密仪器
    • 困难，且容错率低
  • 近似思路（软惩罚）​ ：尽量接近，允许少许偏差
    • 安装弹性装置，偏离时产生回弹力。偏得越远，回弹力越大
    • 也就是这里描述的内容思路（即 使用 "拉格朗日函数"这个"弹性装置"）
      • 新的目标 = 旧的目标 + 惩罚项​​
      • 即 ​​L(x) = f(x) + α * c(x)

一种至少近似地满足约束优化问题的方法：采用拉格朗日函数 。

  • 除了满足 之外，只需将 添加到目标函数 。
  • 这样可以确保不会严重违反约束。

实际例子：权重衰减

  • （多层感知机实现------ 动手学深度学习4.2~4.9_多层感知机开源代码-CSDN博客中的 权重衰减（L2正则化）防止过拟合）
  • 在目标函数中加入 (惩罚项)，以确保 不会增长太大。
  • (该惩罚项，就是拉格朗日函数中的 α * c(x)！)
    • 若某个权重 w 变得很大，其平方 w²会更大，惩罚项的值就会急剧增大
    • 从而"警告"模型，让其收敛一点。
    • 模型为了降低总的损失，就会自发地把权重值控制在一个合理的范围内。
  • 使用约束优化的观点，可以看到，
    • 对于若干半径 r ，这将确保
    • 通过调整 的值，我们可以改变 的大小

**添加惩罚（软约束/惩罚项）**是确保近似满足约束的一种好方法。实践中也确实证明其比精确满足约束更可靠。此外，对于非凸问题，许多使精确方法在凸情况下的性质（例如，可求最优解）不再成立。

2.3.3. 投影 (找最近)（满足约束条件的另一种策略）

满足约束条件的另一种策略是投影（projections）。

例子1：梯度裁剪（防止"步子太大"）

  • ||g|| ：梯度向量的长度
  • θ：设定的值（界限）
  • 相当于要求梯度向量 g必须在一个"半径为 θ 的球"内
  • 也就是说：这就是 在半径为 的球上的投影（projection）。

例子2：更一般的情况

  • 在凸集 上的投影被定义以下公式，它是 中离 最近的点。
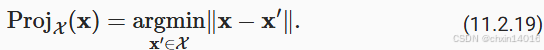
  • ：允许待的区域（如，呼啦圈）
  • x ：当前的位置（如，飞镖落下的点）
  • argmin: 这是一个数学符号，意思是"寻找一个能使后面表达式最小的值"
  • ||x - x'||: 两点之间的距离
  • 所以，整个式子的意思就是：
    • 在允许的区域 X里，找到一个点 x'，使得这个点 x'到现在实际的位置 x的距离最小。
    • 这个点 x'就是投影点。

图像解释：
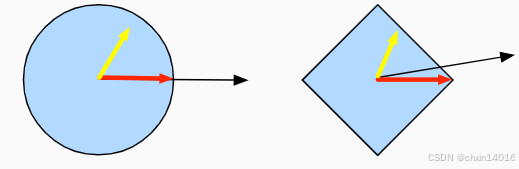图11.2.4 Convex Projections

如 图11.2.4：有两个凸集，一个圆和一个菱形。

  • 黄色：集合内的点
    • 在投影期间保持不变（因为本身就在集合内）
  • 黑色 ：集合 之外 的点
    • 投影到集合中 接近原始黑点 的红点 位置（因为没在集合内，需投影回集合内）
  • 虽然对 的球面来说，方向保持不变，但一般情况下不需要这样。

凸投影的一个用途：计算稀疏权重向量。在本例中，我们将权重向量投影到一个 的球上， 这是 图11.2.4中菱形例子的一个广义版本。

机制对比：惩罚 vs 投影

特性 惩罚法 投影法
​​核心动作​​ ​​往回拉​​ ​​找最近​​
​​工作方式​​ ​​持续施加"修正力"​​ ​​在越界时"瞬移"回边界​​
​​执行时机​​ ​​在整个优化过程中持续作用​​ ​​在每次迭代后进行检查和修正​​
​​约束满足度​​ ​​软约束​​（近似满足，允许轻微越界） ​​硬约束​​（严格满足，绝不允许越界）
​​比喻​​ ​​弹簧/橡皮筋​​ ​​魔法结界/传送门​​

小结

在深度学习的背景下，

  • 凸函数 的主要目的： 帮助 详细了解优化算法 。

    • 由此得出梯度下降法和随机梯度下降法是如何相应推导出来的。

  • 凸集的

    • 交点是凸的

    • 并集不是

  • 詹森不等式：

    • "一个多变量凸函数的总期望值" >= "用每个变量的期望值计算这个函数的总值"

  • 一个二次可微函数是凸函数，当且仅当其Hessian（二阶导数矩阵）是半正定的。

  • 凸约束可以通过拉格朗日函数来添加。

    • 在实践中，只需在目标函数中加上一个惩罚即可。

  • 投影：映射到 凸集中 最接近原始点的点。

3. 梯度下降

梯度下降（gradient descent）很少直接用于深度学习，但其是理解 随机梯度下降算法 的关键。

  • 例如，学习率过大，可能会导致优化问题发散，这种现象早已在梯度下降中出现。
  • 同样地，预处理（preconditioning）是梯度下降中的一种常用技术，还被沿用到更高级的算法中。 下面从简单的一维梯度下降开始。

梯度下降算法：（下山策略）

  1. 感受坡度（计算梯度）​ ：用脚感受脚下山坡向哪个方向最陡。该"最陡下坡方向"就是​梯度​ 。
    1. 一维时，就是导数 f'(x)，它告诉你向左走还是向右走下山更快。
  2. 决定步幅（选择学习率 η）​ ：决定每步迈多大。这个步长就是​学习率 (η)​ 。
    1. 步幅太大（η 太大）​：可能会迈过头，冲到对面的山坡上，甚至越走越高。
    2. 步幅太小（η 太小）​：下山速度会慢，很久都到不了谷底。
  3. 走一步（参数更新）​ ：朝着感觉最陡的下坡方向，迈出一步。（对应 公式11.3.4）
    1. 公式11.3.4：
  4. ​重复​：到了新位置后，停下来，再次用脚感受坡度，然后继续迈出下一步。如此反复。

核心思想：​​

  • 沿着当前最陡的下坡方向（负梯度方向）移动，就能保证函数值下降。
  • 不断重复该过程，最终就能接近最低点。

3.1. 一维梯度下降

以下用【一维中的梯度下降】来严格证明：

  • 为什么梯度下降算法可以优化目标函数？
  • 即 ​"为什么朝着负梯度方向迈一步，高度一定会下降"。

考虑一类连续可微实值函数 ， 利用泰勒展开，可以得到
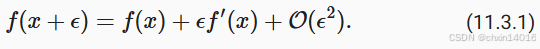在当前位置x附近，整个复杂的山形，可 ​近似看成一条直线​ 。
该直线的斜率就是脚下感受到的坡度 f'(x)。
所以， 移动一小段距离 ε 后，高度大概会变化 ε * f'(x)。

f(x + ε) ≈ f(x) + εf'(x)是一个 ​线性近似​ 。它用直线(切线)来模拟函数在 x附近的行为。
𝓞(ε²)这个项：代表的是"用直线模拟曲线所产生的所有误差"
是因为函数是 ​曲线​ 而不是直线，所以用"直尺"去量所产生的 ​误差​

比如 f(x) = x²，想知道在 x=1附近，f(1+ε)是多少。

  • 精确值（曲线真正的值）​ ：f(1+ε) = (1+ε)² = 1 + 2ε + ε²
  • ​线性近似（切线给出的值）​ ：f(1) + εf'(1) = 1² + ε * (2 * 1) = 1 + 2ε

现在对比一下：

  • 精确值：1 + 2ε + ε²
  • 近似值：1 + 2ε

差值正好为 ε²！​ ​在该例子里，𝓞(ε²)这项就是 ε²。

∴ 这个公式更完整的写法是：

  • f(x + ε) = f(x) + εf'(x) + [我们忽略掉的高阶误差项]

而 𝓞(ε²)就是用来描述这个误差项的大小的。

𝓞(ε²)是一个数学符号，意思是"​​这个误差的量级大约是 ε 的平方​​"。它告诉我们两件重要的事：

  1. 误差有多小​ 。当移动量 ε极小时，ε²会比 ε还要小得 多得多，比如 ε = 0.01，那么 ε² = 0.0001。即 当 ε很小时，线性近似非常精确。
  2. 在梯度下降法中，可以放心地忽略 𝓞(ε²)这项，因为​学习率 η（也就是这里的 ε）通常很小​ 。当选择 ε = -η f'(x)时，我们关心的是函数值下降的方向和趋势。只要一步的步长η足够小，由线性近似带来的误差 𝓞(η²)就会远远小于我们真正关心的那一项 η (f'(x))²，因此不会影响"下山"的大方向。
  • 即在一阶近似中， 可通过 处的函数值 和一阶导数 得出。
  • 可以假设在负梯度方向上移动的 会减少 。
  • 为简单起见，选择固定步长 ，然后取 。将其代入泰勒展开式可以得到

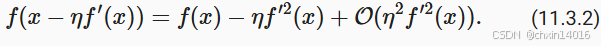选择步长为 ε = -η f'(x)​ ： ​-f'(x)​ ，即 ​负的坡度方向​ 。
若坡度为正（f'(x) > 0，意味着 左低右高 /），则 -f'(x)为负，就会向左走（x↓）
若坡度为负（f'(x) < 0，意味着 左高右低 \），则 -f'(x)为正，就会向右走（x↑）
总之就是，总是在往"下坡"走。​

  • 即新的高度变成了：新高度 ≈ 旧高度 - η * (坡度)²，如公式11.3.4的标题注释。

若其导数 没有消失，就能继续展开，这是因为 。此外，我们总是可以令 小到足以使高阶项变得不相关。因此，
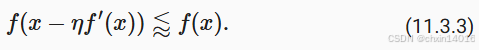​公式 (11.3.2) 和 (11.3.3) f(x - η f'(x)) ≈ f(x) - η (f'(x))²​ ：
把移动的步子和方向代入那个近似公式里，就会发现新的高度变成了：
​新高度 ≈ 旧高度 - η * (坡度)²​
∵ η和 (坡度)²永远是正数 ∴ ​新高度 < 旧高度​ 总是成立！
​这就严格证明了：
只要坡度不为零，按照这个方法走一步，高度就一定会在这一步内下降

这意味着，若我们使用 以下(公式11.3.4) 来迭代 ，函数 的值可能会下降：
走一步（参数更新）​ ：朝着感觉最陡的下坡方向，迈出一步。
​x（新位置） = x（旧位置） - η（步长） * f'(x)（坡度）

  • 因此，在梯度下降中，首先选择初始值 和常数 ， 然后使用它们连续迭代 ，直到停止条件达成。
  • 停止条件可设为：
    • 当梯度 的幅度足够小 或
    • 迭代次数达到某个值时

下面展示如何实现梯度下降。

  • 为简单起见，选用目标函数 。
  • 尽管知道 时 能取得最小值，但仍然使用这个简单的函数来观察的变化：
  • 导数（坡度）​ 是 f'(x) = 2x
  • ​更新公式​ 是 x = x - η * 2x

假设从 x=2开始，学习率 η=0.1：

  • 第一步：坡度=2*2=4。更新：x = 2 - 0.1 * 4 = 1.6。
    • 高度：2² = 4 → 1.6² = 2.56
  • 第二步：坡度=2*1.6=3.2。更新：x = 1.6 - 0.1 * 3.2 = 1.28。
    • 高度继续下降：1.6² = 2.56 → 1.28² = 1.6384
  • 如此反复，就会一步步走向谷底 x=0
python 复制代码 
# %matplotlib inline
import numpy as np
import torch

def f(x):  # 目标函数 f(x) = x²
    return x ** 2

def f_grad(x):  # 目标函数的梯度(导数) f'(x) = 2x
    return 2 * x

接下来，

  • 使用 x=10 作为初始值，并假设 。
  • 使用梯度下降法迭代 x 共10次。

可以看到，x 的值最终将接近最优解。

python 复制代码 
def gd(eta, f_grad):
    x = 10.0 # 初始值
    results = [x]
    for i in range(10): # 迭代10次
        x -= eta * f_grad(x)
        results.append(float(x))
        print(f"epoch ：{i+1}，当前x={x:.7f}")
    print(f'epoch 10, x: {x:f}')
    return results

results = gd(0.2, f_grad) # 传入0.2的学习率(步长大小)，和对应导数(坡度)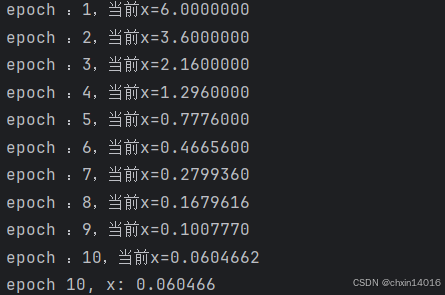

对进行 x 优化的过程可以绘制如下：

python 复制代码 
def show_trace(results, f):
    """
    可视化梯度下降的轨迹
    results: 列表，存储梯度下降过程中每次迭代的x值
    f: 目标函数，接受x作为输入并返回函数值
    """
    # 确定绘图范围：取results中绝对值最大的x值，作为绘图边界
    n = max(abs(min(results)), abs(max(results)))

    # 生成平滑的函数曲线x坐标（从-n到n，步长0.01）
    f_line = torch.arange(-n, n, 0.01)

    # 绘制两个图形：
    # 1、目标函数的完整曲线（f_line对应的f(x)）
    # 2、梯度下降过程中各点的位置（results对应的f(x)）
    plot([f_line, results], # x轴数据：函数曲线x值 + 迭代点x值
        [[f(x) for x in f_line],      # 完整函数曲线y值
         [f(x) for x in results]],    # 迭代点对应的y值
        'x', 'f(x)',
        fmts=['-', '-o']) # 线型：实线表示函数，带圆点的实线表示迭代轨迹

common.show_trace(results, f) # 显示梯度下降轨迹

3.1.1. 学习率：需与批量大小匹配 (大批量→大学习率)

学习率（learning rate）：决定目标函数

  1. 能否收敛到局部最小值
  2. 何时收敛到最小值
  • 学习率 可由算法设计者设置。
  • 注意，
    • 学习率过小，会导致 的更新非常缓慢，需要更多的迭代。
    • 例如，考虑同一优化问题中 的进度。
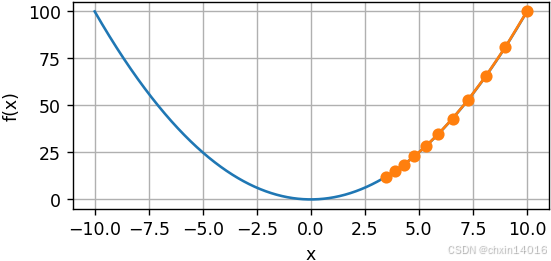
    • 如下所示，经过10个步骤后，仍然离最优解很远。
python 复制代码 
common.show_trace(gd(0.05, f_grad), f) # 学习率改为0.05，可视化梯度下降轨迹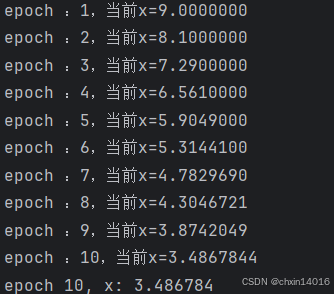

  • 相反，若学习率过高， 对于一阶泰勒展开式可能太大。
  • 即，(11.3.1) 中的 可能变得显著了。
  • 在这种情况下，x 的迭代不能保证降低 f(x) 的值。
  • 例如，当学习率为 时，x 超出了最优解 x=0 并逐渐发散。
python 复制代码 
common.show_trace(gd(1.1, f_grad), f) # 学习率改为1.1，可视化梯度下降轨迹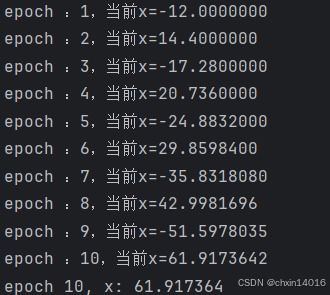

3.1.2. 局部最小值

  • 为了演示非凸函数的梯度下降，
    • 考虑函数 ，其中 为某常数。
    • 该函数
      • 是一个振荡函数，随着|x|增大，振幅线性增长
      • 周期约为 2π/(0.15π) ≈ 13.33
      • 因此，会有无穷多个局部最小值。
    • 根据所选的学习率，最终可能只会得到许多解中的其中一个。
    • 下面的例子说明了（不切实际的）高学习率如何导致较差的局部最小值：

对函数 f(x) = x * cos(c*x) 求导，得到其梯度 f'(x)：

  • 乘积法则 ：f(x) = u(x) * v(x) ，则 d(u*v)/dx = u' * v + u * v'
    • u(x) = x → u'(x) = 1
    • v(x) = cos(c*x)
  • 链式法则 ：对 v(x) = cos(c*x) 求导
    • 设内函数 g(x) = c*x，外函数 h(g) = cos(g)，
      • g(x) = c*x → g'(x) = c
      • h(g) = cos(g) → h'(g) = -sin(c*x)
    • 则导数：v'(x) = h'(g) * g'(x) = -sin(c*x) * c

f'(x) = u' * v + u * v'

= 1 * cos(c*x) + x * (-sin(c*x) * c)

= cos(c*x) - c * x * sin(c*x) = 最终梯度公式

python 复制代码 
c = torch.tensor(0.15 * np.pi) # 预定义的常数 c = 0.15π ≈ 0.4712

def f(x):  # 目标函数 f(x) = x * cos(c * x)
    return x * torch.cos(c * x)

def f_grad(x):  # 目标函数的梯度 f'(x) = cos(c*x) - c*x*sin(c*x)
    return torch.cos(c * x) - c * x * torch.sin(c * x)

common.show_trace(gd(2, f_grad), f) # 学习率设为2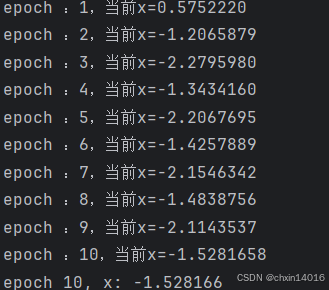

3.2. 多元梯度下降

  • 前面已讲过单变量的情况，现在考虑 的情况。
  • 即目标函数 将向量映射成标量。
  • 相应地，它的梯度也是多元的 ，它是一个由 d 个偏导数组成的向量：

∇f(x) 是一个 ​ 由 ​偏导数​ 组成的 向量
偏导数："只考虑一个方向时的坡度"，比如：
∂f/∂x₁：若 只朝东（x₁方向）​ 移动一小步，海拔会变化多少。这就是东边的坡度
∂f/∂x₂：若 只朝北（x₂方向）​ 移动一小步，海拔会变化多少。这就是北边的坡度
把各个方向上的坡度组合起来，就得到了指向"最陡上坡方向"的梯度。

  • 梯度中的每个偏导数元素 ：代表了当输入 时 在 x 处的变化率

与先前单变量的情况一样，可以对多变量函数使用相应的泰勒近似来思考。具体来说，

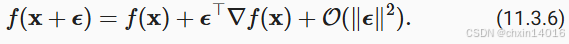
换句话说，在 的二阶项中，最陡下降的方向由负梯度 得出。选择合适的学习率 来生成典型的梯度下降算法：
知道了最陡的下坡方向（负梯度），开始迈出一步

  • ​x​ ：当前所处位置（一个坐标，比如 [东经, 北纬]）
  • ​∇f(x)​ ：在当前所处位置，最陡的​上坡​方向
  • ​-∇f(x)​ ：最陡的​下坡​方向
  • ​η（学习率）​ ：这一步要​走多远​。步长太大可能过头；步长太小则下山太慢
  • x - η∇f(x)​ ：从当前位置，沿着最陡下坡方向走 η 这么远，到达的新位置

这个算法在实践中的表现如何呢？

  • 构造一个目标函数 ，
  • 输入：二维向量
  • 输出：标量
  • 梯度：由 给出。
  • 初始位置： [-5, -2]

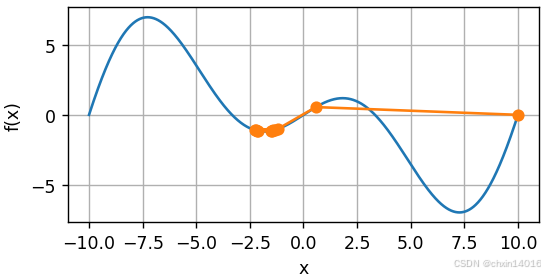
通过梯度下降观察 x 的轨迹。此外仍需两个辅助函数：

  1. update函数，将其应用于初始值20次；
  2. 绘图函数 show_trace_2d()：用于显示 x 的轨迹
python 复制代码 
def train_2d(trainer, steps=20, f_grad=None):  #@save
    """用定制的训练机优化2D目标函数
    trainer : 训练函数，执行单步参数更新
    steps   : 训练步数（迭代次数）
    f_grad  : 梯度计算函数（可选）
    返回: 包含所有迭代点(x1, x2)的列表
    """
    # s1和s2是稍后将使用的内部状态变量
    # 初始化：从点(-5, -2)开始，s1和s2是为后续高级优化器预留的状态变量
    x1, x2, s1, s2 = -5, -2, 0, 0
    results = [(x1, x2)] # 存储轨迹点
    for i in range(steps):
        if f_grad: # 若有梯度函数，传入梯度进行计算
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2, f_grad)
        else: # 否则直接使用训练器
            x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2)) # 记录新位置
    print(f'epoch {i + 1}, x1: {float(x1):f}, x2: {float(x2):f}')
    return results

def show_trace_2d(f, results):  #@save
    """显示优化过程中2D变量的轨迹
    f      : 目标函数，用于绘制等高线
    results: 优化轨迹点列表 [(x1, x2), ...]
    """
    # 1. 绘制优化轨迹（橙色圆点连线）
    ''' zip(*results)作用：进行数据转置
    把 原始数据（列表的列表）：
            [ (x1_1, x2_1),
              (x1_2, x2_2),
              ... ]
    转换为 转置后：
            [ (x1_1, x1_2, ...), 
              (x2_1, x2_2, ...) ]
    *results：将列表解包，相当于把 results的每个元素作为单独参数传递给 zip
    zip     ：按位置重新组合元素
    效果：
        x1_coords = (-5, -4.0, -3.2, ...)   即 所有点的x坐标
        x2_coords = (-2, -1.2, -0.72, ...)  即 所有点的y坐标
    '''
    x1_coords, x2_coords = zip(*results)  # 将[(x1,y1),(x2,y2)...]拆分为两个列表
    plt.plot(x1_coords, x2_coords, '-o', color='#ff7f0e')

    # 2. 创建网格用于绘制等高线
    x1_range = torch.arange(-5.5, 1.0, 0.1)  # x1从-5.5到1.0，步长0.1
    x2_range = torch.arange(-3.0, 1.0, 0.1)  # x2从-3.0到1.0，步长0.1
    # 通过 torch.meshgrid()生成两个网格坐标矩阵，包含所有网格点的 (x1,x2) 坐标
    x1_grid, x2_grid = torch.meshgrid(x1_range, x2_range, indexing='ij')

    # 3. 计算网格点上目标函数值并绘制等高线
    z = f(x1_grid, x2_grid)  # 计算每个网格点的函数值 (在每个网格点计算的函数值矩阵)
    plt.contour(x1_grid, x2_grid, z, colors='#1f77b4') # 蓝色等高线
    ''' 会绘制出一系列蓝色闭合曲线：
    每条曲线表示函数值相等的点（等高线）
    曲线越密集表示坡度越陡
    中心的闭合圈对应最小值点（本例中为 (0,0)）
    '''

    # 4. 设置坐标轴标签
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.title('2D Gradient Descent Trajectory')
    plt.grid(True, linestyle='--', alpha=0.7)
    plt.show()
  • 接下来，观察学习率 时优化变量 x 的轨迹。
  • 可以看到：
    • 经过20步之后，x 的值接近其位于 [0, 0] 的最小值。
    • 虽然进展相当顺利，但相当缓慢。

f(x) = x₁² + 2x₂²的求导过程：

1. 梯度定义

2. 对 x₁ 求偏导

3. 对 x₂ 求偏导

4. 最终梯度

将两个偏导数组合成梯度向量：

这就是函数 f(x) = x₁² + 2x₂²在任意点 (x₁, x₂)处的梯度。

∴ 这里的梯度下降更新公式：

5. 几何意义

梯度向量 [2x₁, 4x₂]告诉我们：

  • ​​方向​ ​：函数在点 (x₁, x₂)处最陡上升的方向

  • ​​大小​​：坡度有多陡

python 复制代码 
def f_2d(x1, x2):  # 目标函数 f(x) = x₁² + 2x₂²
    return x1 ** 2 + 2 * x2 ** 2

def f_2d_grad(x1, x2):  # 目标函数的梯度：[∂f/∂x1, ∂f/∂x2] = [2x1, 4x2]
    return (2 * x1, 4 * x2)

def gd_2d(x1, x2, s1, s2, f_grad):
    """标准的梯度下降更新规则
    x1, x2: 当前参数值
    s1, s2: 状态变量（在此简单GD中未使用）
    f_grad: 梯度计算函数
    返回: 更新后的参数和状态 (new_x1, new_x2, 0, 0)
    """
    g1, g2 = f_grad(x1, x2) # 计算梯度
    # 梯度下降更新：x ← x - η * ∇f(x)
    new_x1 = x1 - eta * g1
    new_x2 = x2 - eta * g2
    return (new_x1, new_x2, 0, 0)  # 返回新参数，状态重置为0

eta = 0.1 # 学习率
# 执行梯度下降并可视化结果
results = common.train_2d(gd_2d, f_grad=f_2d_grad)
common.show_trace_2d(f_2d, results)

3.3. 自适应方法

如（3.1.1. 学习率）中所示，选择"恰到好处"的学习率 很棘手。

  • 若把它选得太小，就没有什么进展；
  • 若太大，得到的解就会振荡，甚至可能发散。

我们期望可以自动确定 ，或者完全不必选择学习率。也就是说，除了考虑目标函数的值和梯度、还考虑它的曲率的二阶方法。

3.3.1. 牛顿法

牛顿法：不仅要感受坡度，还要感受地面的弯曲程度（二阶导数）​​。

  • 核心思想 ：​利用二阶导数( 曲率**)信息动态调整步长​** (自动计算最优步长​​)，相比梯度下降能更智能地确定更新量。
  • 实际应用情况 ：
    • 简单问题：收敛快
    • 深度学习：计算成本高
    • 但思想启发了许多现代高级优化算法（如AdaGrad, Adam等），这些算法试图以更低的成本模拟牛顿法的优点。
  • 困境 ：计算代价太高​
    • Hessian矩阵太大
    • 求逆困难

Hessian矩阵（H）​ ​：用于描述​​各个方向上的弯曲程度​​。

回顾一些函数 的泰勒展开式，事实上我们可以把它写成
ε：移动的距离，即位移向量
​∇f(x)（梯度）​： ​一阶信息​
εᵀ ∇f(x)： ​核心的一阶预测​ 。点乘 εᵀ确保了只有沿着风向(从市中心指向小镇)的分量才被计算在内
∇²f(x)（Hessian矩阵）：二阶信息​ ，描述了变化趋势 ​本身是如何变化的
1/2 εᵀ ∇²f(x) ε：更精细的二阶修正​ 。(修正误差)
O(‖ε‖³)：无法预料的突发情况影响 (当预测时间不长(ε很小)、区域不大时，该影响极小，可忽略)

  • ​一阶近似（梯度下降法的基础）： 预测温度 ≈ 当前温度 + 风的影响​
    • ​优点​：计算简单快捷
    • ​缺点​：不够精确，因为它忽略了地形等复杂因素。这就像梯度下降法，只知道往下走，但不知道步子该迈多大
  • 二阶近似（牛顿法的基础）​： 预测温度 ≈ 当前温度 + 风的影响 + 地形的修正
    • 优点​：预测非常精确
    • ​缺点​：获取"气候地形图"（Hessian矩阵）和计算修正值非常困难且昂贵
  • 总结：
    • 任何一个平滑的、复杂的函数 f在某个点 x的附近，其行为都可以被分解为：
      • 一个常数（当前值）​
      • ​一个线性部分（当前的变化趋势/梯度）
      • 一个弯曲部分（趋势的变化率/Hessian）
    • 在优化算法中的应用：​
      • 梯度下降​ 只用了第1、2部分(知道当前高度和坡度)，所以像盲人，只能试探着下山。
      • 牛顿法​ 用了第1、2、3部分(还知道了地面的弯曲程度)，所以能"看见"整个山谷的形状，从而能直接计算出最优的步长，快速到达谷底。

为避免繁琐的符号，我们将 定义为 的Hessian，是 d×d 矩阵。

  • 当 d 的值很小且问题简单时， 很容易计算。
  • 但是对于深度神经网络而言，考虑到 可能非常大， 个条目的存储代价会很高，此外通过反向传播进行计算可能雪上加霜。
  • 然而，姑且先忽略这些考量，看看会得到什么算法。

毕竟， 的最小值满足 。 遵循 2.4节中的微积分规则， 通过取 对 (11.3.8)的导数， 再忽略不重要的高阶项，我们便得到
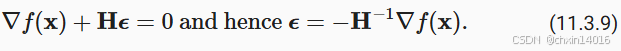ε = - H⁻¹ * ∇f(x)

  • ∇f(x)：还是原来的坡度（梯度）
  • H⁻¹：这是Hessian矩阵的逆，可以理解为 ​"自适应步长调节器"​
    • ​H⁻¹的作用：根据地形曲率，自动计算出一个"恰到好处"的步长

也就是说，作为优化问题的一部分，需要将Hessian矩阵 求逆。

举一个简单的例子：用 这个简单的碗状函数举例。

  • 我们有
    • 梯度（坡度）​ ：
    • ​Hessian（曲率）​ ： （因为二阶导数是1，表示这个碗的弯曲程度是均匀的）
  • 因此，对于任何 x ，我们可以获得 。
    • 牛顿法步长​ ：ε = - H⁻¹ * ∇f(x) = - (1)⁻¹ * x = -x
    • 效果​ ：
      • 无论从哪个点 x开始，牛顿法都会直接让你一步跳到 x + ε = x - x = 0，也就是碗底最低点。
      • 因为牛顿法通过曲率信息"知道"这个碗是对称且均匀的，它能够精确计算出需要迈多大一步才能直达谷底。
  • 换言之，单单一步就足以完美地收敛，而无须任何调整。 我们在这里比较幸运：泰勒展开式是确切的，因为 。

下面看看其他问题。

示例一：凸双曲余弦函数
  • 给定一个凸双曲余弦函数 c ，其中 c 为某些常数。
  • 可以看到经过几次迭代后，得到了 x=0 处的全局最小值：

双曲函数求导

目标函数：f(x) = cosh(c*x)

  • ​​一阶导数​​：

    f'(x) = d/dx [cosh(c*x)] = c * sinh(c*x)

    （双曲余弦的导数是双曲正弦）

  • ​​二阶导数​​：

    f''(x) = d/dx [c * sinh(c*x)] = c² * cosh(c*x)

    （双曲正弦的导数是双曲余弦）

python 复制代码 
c = torch.tensor(0.5) # 常数系数

def f(x):  # O目标函数：双曲余弦函数，形状类似开口向上的抛物线
    return torch.cosh(c * x)

def f_grad(x):  # 目标函数的梯度（一阶导数）
    # f'(x) = d/dx [cosh(c*x)] = c * sinh(c*x)
    return c * torch.sinh(c * x) # 双曲正弦函数是双曲余弦的导数

def f_hess(x):  # 目标函数的Hessian（二阶导数，即 Hessian标量）
    # f''(x) = d/dx [c * sinh(c*x)] = c² * cosh(c*x)
    return c**2 * torch.cosh(c * x) # 双曲余弦的二阶导仍是双曲余弦

def newton(eta=1):
    """牛顿法优化器
    eta(η)：控制更新步长的缩放因子
            通常设为1，不稳定时可降低0.1-0.5
    """
    x = 10.0  # 初始点
    results = [x]  # 记录轨迹
    for i in range(10):
        # 牛顿法更新公式：x ← x - η * f'(x)/f''(x)
        ''' 牛顿法更新公式解析
        数学形式：x_{k+1} = x_k - η * [∇²f(x_k)]⁻¹ * ∇f(x_k)
        对于单变量情况：
        [∇²f(x_k)]⁻¹简化为 1/f''(x_k)
        因此更新公式简化为 x_k - f'(x_k)/f''(x_k)
        '''
        x -= eta * f_grad(x) / f_hess(x)
        results.append(float(x))
    print('epoch 10, x:', x)
    return results

common.show_trace(newton(), f)
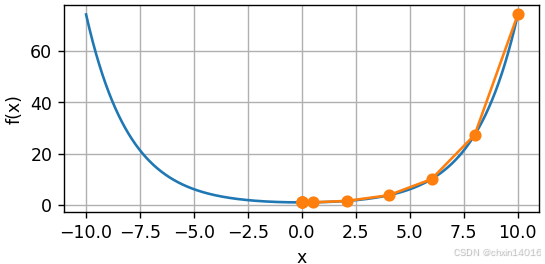
  • 函数形状：平滑的开口向上曲线
  • 牛顿法特性：由于函数是严格凸的，牛顿法会快速收敛到全局最小值
示例二：非凸函数
  • 比如 ， 为某些常数。
  • 注意：
    • 在牛顿法中，最终都要除以Hessian。
    • 也就是说，若二阶导数为负，则 的值可能会趋于增加。
    • 这是该算法的致命缺陷！下面看看实践中会发生的情况：

振荡函数求导

目标函数：f(x) = x * cos(c*x)

  • ​​一阶导数​​（乘积法则）：

    f'(x) = d/dx [x] * cos(c*x) + x * d/dx [cos(c*x)]

    = 1 * cos(c*x) + x * (-c * sin(c*x))

    = cos(c*x) - c*x*sin(c*x)

  • ​​二阶导数​​：

    f''(x) = d/dx [cos(c*x)] - c * d/dx [x*sin(c*x)]

    = -c*sin(c*x) - c*[sin(c*x) + x*c*cos(c*x)]

    = -2c*sin(c*x) - c²x*cos(c*x)

python 复制代码 
c = torch.tensor(0.15 * np.pi) # 常数系数

def f(x):  # 目标函数：振荡函数
    # c：控制函数振荡频率(值越大函数振荡越剧烈)
    return x * torch.cos(c * x) # 产生周期性振荡的函数

def f_grad(x):
    ''' 目标函数的梯度（一阶导数）
    目标函数：f(x) = x * cos(c*x)
    一阶导数（乘积法则）：
    f'(x) = d/dx [x] * cos(c*x) + x * d/dx [cos(c*x)]
          = 1 * cos(c*x) + x * (-c * sin(c*x))
          = cos(c*x) - c*x*sin(c*x)
    '''
    return torch.cos(c * x) - c * x * torch.sin(c * x)

def f_hess(x):
    ''' 目标函数的Hessian（二阶导数）
    目标函数：f(x) = x * cos(c*x)
    二阶导数：
    f''(x) = d/dx [cos(c*x)] - c * d/dx [x*sin(c*x)]
           = -c*sin(c*x) - c*[sin(c*x) + x*c*cos(c*x)]
           = -2c*sin(c*x) - c²x*cos(c*x)
    '''
    return - 2 * c * torch.sin(c * x) - x * c**2 * torch.cos(c * x)

common.show_trace(newton(), f)      # 学习率为1.0

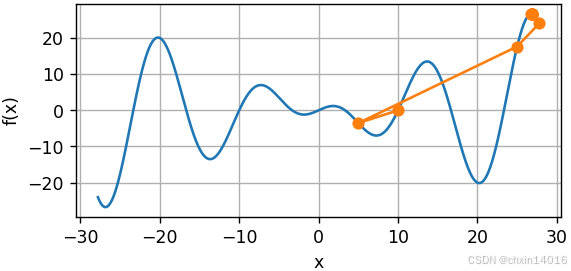
这发生了明显的错误。想要修正它有两个策略：

  • 策略一：用取Hessian的绝对值来修正。
  • 策略二：重新引入学习率。
    • 这似乎违背了初衷，但不完全是------拥有二阶信息可使我们
      • 在曲率较大时保持谨慎，
      • 而在目标函数较平坦时则采用较大的学习率。

下面看看在学习率稍小的情况下它是如何生效的，比如 。如图所示，我们有了一个相当高效的算法。

python 复制代码 
common.show_trace(newton(0.5), f)   # 学习率为0.5
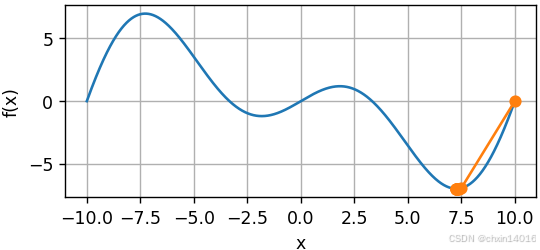
  • 函数形状：周期性振荡的波形
  • 牛顿法表现：
    • 当 η=1 时：可能因步长过大而在极值点附近振荡
    • 当 η=0.5 时：减小步长后能更稳定收敛

黑塞矩阵获取过程

  • 对于单变量函数，Hessian就是二阶导数 ：

    • 双曲函数：H = c² * cosh(c*x)
    • 振荡函数：H = -2c*sin(c*x) - c²x*cos(c*x)

  • 对于多变量函数时，Hessian是一个对称矩阵：

    bash 复制代码 
    H = [[∂²f/∂x₁², ∂²f/∂x₁∂x₂],
     [∂²f/∂x₂∂x₁, ∂²f/∂x₂²]]

牛顿法 vs. 梯度下降

特性 梯度下降法 牛顿法
​​使用信息​​ 一阶导数（坡度） 一阶导数 + 二阶导数（坡度 + 曲率）
​​步长选择​​ 需要手动设定学习率 η ​​自动计算​ ​最优步长 H⁻¹
​​收敛速度​​ 较慢，小步迭代 ​​极快​​，尤其对于简单函数可能一步到位
​​计算成本​​ 低 ​​非常高​​（需计算和求逆Hessian矩阵）

牛顿法的困境：计算代价太高​​。

  • ​Hessian矩阵太大​ ：深度学习模型可能有数百万甚至数十亿的参数。Hessian矩阵的尺寸是 [参数数量 x 参数数量]。对于一个100万参数的模型，Hessian矩阵将有 ​1万亿个元素​，根本无法存储和计算。
  • 求逆困难​：对如此巨大的矩阵求逆，在计算上是不可行的。

核心思想：

  1. 牛顿法 是一种更强大的优化算法，它通过利用二阶导数（曲率）信息，能自动计算最优步长​​，从而解决梯度下降中"学习率难选"的问题。
  2. 对于简单问题 ，牛顿法收敛 速度极快。
  3. 但对于深度学习 ，牛顿法直接应用的计算成本高得无法承受。
  4. 牛顿法的思想启发了许多现代高级优化算法（如AdaGrad, Adam等），这些算法试图以更低的成本模拟牛顿法的优点。

所以，牛顿法更像是一个"理想中的完美算法"，为我们指明了改进方向，尽管它本身不适用于深度学习。

3.3.2. 收敛性分析（牛顿法的收敛速度）

牛顿法在接近最优解时具有"二次收敛"特性​​，这意味着：

  1. 前期可能较慢​：离解远时，二阶信息可能不准确
  2. 后期极快​：一旦进入解的"邻域"，误差会以平方速度爆炸性缩小
  3. 需要函数"友好"​：要求函数光滑、高阶导数有界

猜价格

  • 梯度下降法（普通人猜）​ ：
    • 每次根据"高了"或"低了"的提示，固定调整一定金额（比如每次调100元）。
    • 越接近真实价格时，调整幅度不变，可能反复横跳。
  • 牛顿法（聪明人猜）​ ：
    • 不仅听提示，还会​分析"误差有多大"​，然后按比例调整。
    • 离得远时大胆调整，离得近时精细微调。

总结：牛顿法就是，越接近答案，误差会以"平方速度"缩小。

以部分目标凸函数 为例，分析其牛顿法收敛速度。

  • 这些目标凸函数三次可微，且二阶导数不为零，即 。

由于多变量情况下的证明是对 以下一维参数情况证明的直接拓展，对理解该问题不能提供更多帮助，因此这里省略了多变量情况的证明。

  • ： 在第 次迭代时的值
  • ：表示 迭代时与最优性的距离，也就是误差 ，或者说是差距
    • 定义误差：e⁽ᵏ⁾ = x⁽ᵏ⁾ - x*，表示 第k次猜的价格 x⁽ᵏ⁾ 和 真实价格 x* 的差距
  • 通过泰勒展开，我们得到条件 可以写成

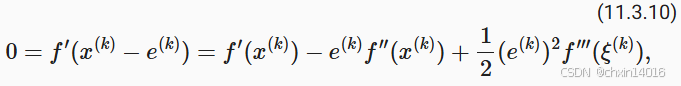最优解 x*处梯度为0（f'(x*) = 0）
而 x* = x⁽ᵏ⁾ - e⁽ᵏ⁾，所以把 f'(x*)在 x⁽ᵏ⁾处展开

这对某些 成立。 将上述展开除以 得到
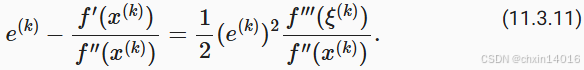得到误差关系

回想之前的方程 。 代入这个更新方程，取两边的绝对值，我们得到
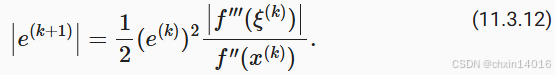得出收敛速度 ①

因此，每当我们处于有界区域 ， 我们就有一个二次递减误差
得出收敛速度 ②

另一方面，优化研究人员称之为"线性"收敛，而将 这样的条件称为"恒定"收敛速度。

  • 注意：我们无法估计整体收敛的速度，但是一旦我们接近极小值，收敛将变得非常快。
  • 另外，这种分析要求 在高阶导数上表现良好，即确保 在如何变化它的值方面没有任何"超常"的特性。
"二次收敛"的魔力，​​举例说明​​：

假设 c = 1，初始误差 e⁽⁰⁾ = 0.1

  • 第1次迭代：e⁽¹⁾ ≤ (0.1)² = 0.01
  • 第2次迭代：e⁽²⁾ ≤ (0.01)² = 0.0001
  • 第3次迭代：e⁽³⁾ ≤ (0.0001)² = 0.00000001

如上所示：误差以平方速度缩小，从0.1到1e-8只需3步。

对比其他方法的收敛速度

方法 收敛速度 比喻 数学表达
​​梯度下降​​ 线性收敛 0.1 → 0.09 → 0.081 → 0.073 → ... （缓慢线性下降） 每次固定缩短10%误差 e⁽ᵏ⁺¹⁾ ≈ 0.9 × e⁽ᵏ⁾
​​牛顿法​​ 二次收敛 0.1 → 0.01 → 0.0001 → 0.00000001 → ... （急剧平方下降） 每次误差平方级缩小 e⁽ᵏ⁺¹⁾ ≈ (e⁽ᵏ⁾)²

3.3.3. 预处理

  • 使用统一的学习率η 的话，会出现梯度下降中的"尺度不匹配"问题：
  • (用同样的力度调两个音响，效果不统一)
    • 音响A​ ：调节旋钮灵敏，轻轻一转音量就变化很大（对应​梯度大​ 的参数）
      • 一动就会音量剧变，难以控制
    • ​音响B​ ：调节旋钮迟钝，需要很大力气才能改变音量（对应​梯度小​ 的参数）
      • 动后音量几乎不变，调整无效

预处理解决方案：给每个参数配个"智能调音师"

"预处理"：

  • 核心思想 ：​不再使用统一的学习率，而是为每个参数定制个性化的步长​。
  • 作用：改善 "计算和存储完整的Hessian非常昂贵" 这个问题。
  • 它回避了计算整个Hessian，而只计算"对角线"项，即如下的算法更新：
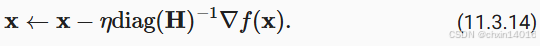
  • ∇f(x)：每个参数当前的"音量偏差"（梯度）
  • diag(H)：每个音响旋钮的"灵敏度"（Hessian矩阵的对角线元素，代表曲率）
  • diag(H)⁻¹：智能调音师的"调节系数"------对灵敏的音响（曲率大）轻轻调，对迟钝的音响（曲率大）用力调

虽不如完整的牛顿法精确，但聊胜于无。假设

  • 变量A：以 毫米 表示高度
  • 变量B：以 公里 表示高度
  • 这两种自然尺度：都以 米 为单位

则此时参数化就出现了严重的不匹配。而使用预处理可以消除这种情况。

  • 梯度下降的有效预处理，相当于为每个变量选择不同的学习率（矢量 的坐标）。
  • 后面一节会看到，预处理推动了随机梯度下降优化算法的一些创新。

3.3.4. 梯度下降和线搜索

梯度下降的一个关键问题：可能会 超过目标 或 进展不足

  • 解决这一问题的简单方法：结合使用线搜索和梯度下降。
  • 也就是说，使用 给出的方向， 然后进行二分搜索，以确定哪个学习率 使 取最小值。

线搜索：在迈步前先沿着下坡方向试探几步，找到最佳落脚点​​。具体操作：

  1. 确定方向​ ：梯度方向 -∇f(x)（最陡的下坡方向）
  2. 沿线搜索​ ：在这个方向上尝试多个步长 η，计算 f(x - η∇f(x))
  3. 选择最优​：选择让目标函数值最小的那个 η

有关分析和证明，此算法收敛迅速（请参见 (Boyd and Vandenberghe, 2004)）。

  • 深度学习中很少用线搜索。因为其实现方式太昂贵了。
  • 线搜索的每一步都需要评估整个数据集上的目标函数(尝试不同 η)，而深度学习的数据集往往巨大，这种计算成本是无法承受的。

预处理 vs 线搜索

方法 解决的问题 核心思想 深度学习适用性
​​预处理​​ 参数尺度不匹配 为每个参数定制步长 ✅ 广泛使用（如Adam优化器）
​​线搜索​​ 学习率选择困难 沿梯度方向找最优步长 ❌ 很少使用（计算成本太高）

小结

  • 学习率的大小很重要：

    • 太大 → 使模型发散

    • 太小 → 没有进展

  • 梯度下降会可能陷入局部极小值，而得不到全局最小值。

  • 在高维模型中，调整学习率是很复杂的。

  • 预处理有助于调节比例。

  • 牛顿法在凸问题中一旦开始正常工作，速度就会快得多。

  • 对于非凸问题，不要不作任何调整就使用牛顿法。

4. 随机梯度下降

  • 前面在（3. 梯度下降）中描述了梯度下降的基本原则。
  • 本节继续更详细地说明随机梯度下降（stochastic gradient descent）。
python 复制代码 
# %matplotlib inline
import math
import torch
import common

标准梯度下降 vs 随机梯度下降

特性 标准梯度下降（全面质检） 随机梯度下降（抽样质检）
​​计算成本​​ O(n)，随数据量线性增长 ​​O(1)，与数据量无关​​
​​更新频率​​ 慢（全量数据算完才更新） ​​快（单个数据就算完更新）​​
​​收敛稳定性​​ 稳定，方向准确 ​​有噪声，但长期方向正确​​
​​适用场景​​ 小数据集 ​​大数据集（深度学习主流）​

4.1. 随机梯度更新

在深度学习中，目标函数通常是 训练数据集中 每个样本的损失函数的平均值。

  • 给定 n 个样本的训练数据集
  • 假设 是关于索引 的训练样本的损失函数
  • 其中 是参数向量。

然后我们得到目标函数（平均损失）：

的目标函数的梯度计算为：（标准梯度下降法，全面质检）

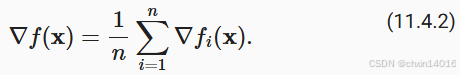
若使用梯度下降法，则每个自变量迭代的计算代价为 ，它随 n 线性增长。因此，当训练数据集较大时，每次迭代的梯度下降计算代价将较高。

随机梯度下降(SGD)：可降低每次迭代时的计算代价。(抽样质检)

  • 在随机梯度下降的每次迭代中，我们对数据样本随机均匀采样一个索引 （随机抽取）
  • 其中 ，并计算梯度 以更新 ：
  • η ：学习率

可以看到，每次迭代的计算代价从梯度下降的 降至常数 。此外，我们要强调，随机梯度 是对完整梯度 的无偏估计(在统计意义上)，因为
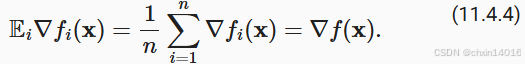​左式​ ：若每天 ​随机抽检1个零件​ ，重复365天，这些抽样结果的平均质量
​右式​ ：全年所有零件的真实平均质量
​结论​ ： ​长期来看，抽样质检的平均结果等于全面质检的结果

这意味着，平均而言，随机梯度是对梯度的良好估计。

  • 现在，将 随机梯度下降 与 标准梯度下降进行比较，
  • 方法是向梯度添加均值为0、方差为1的随机噪声，以模拟随机梯度下降。
python 复制代码 
def f(x1, x2):  # 目标函数 f(x) = x₁² + 2x₂²
    return x1 ** 2 + 2 * x2 ** 2

def f_grad(x1, x2):  # 目标函数的梯度：[∂f/∂x1, ∂f/∂x2] = [2x1, 4x2]
    return 2 * x1, 4 * x2

def sgd(x1, x2, s1, s2, f_grad):
    """ 随机梯度下降更新
    x1, x2: 当前参数值
    s1, s2: 状态变量（为动量法等预留的，此处未使用）
    f_grad: 梯度计算函数
    返回: 更新后的参数和状态 (new_x1, new_x2, 0, 0)
    """
    g1, g2 = f_grad(x1, x2) # 计算真实梯度
    # 添加均值为0、标准差为1的高斯噪声
    # 模拟有噪声的梯度（添加随机噪声，模拟SGD的批次采样中批次梯度的不确定性）
    g1 += torch.normal(0.0, 1, (1,)).item() # 给x1梯度加噪声
    g2 += torch.normal(0.0, 1, (1,)).item() # 给x2梯度加噪声
    eta_t = eta * lr() # 计算当前步长（此处学习率固定，固定为 0.1 * 1 = 0.1）
    # 参数更新：x ← x - η * (∇f(x) + noise)，即带噪声的梯度下降
    return (x1 - eta_t * g1, x2 - eta_t * g2, 0, 0) # 返回新参数和清零状态

def constant_lr():
    return 1 # 固定学习率系数

eta = 0.1         # 基础学习率
lr = constant_lr  # 学习率函数（此处为常数）
common.show_trace_2d(f, common.train_2d(sgd, steps=50, f_grad=f_grad))


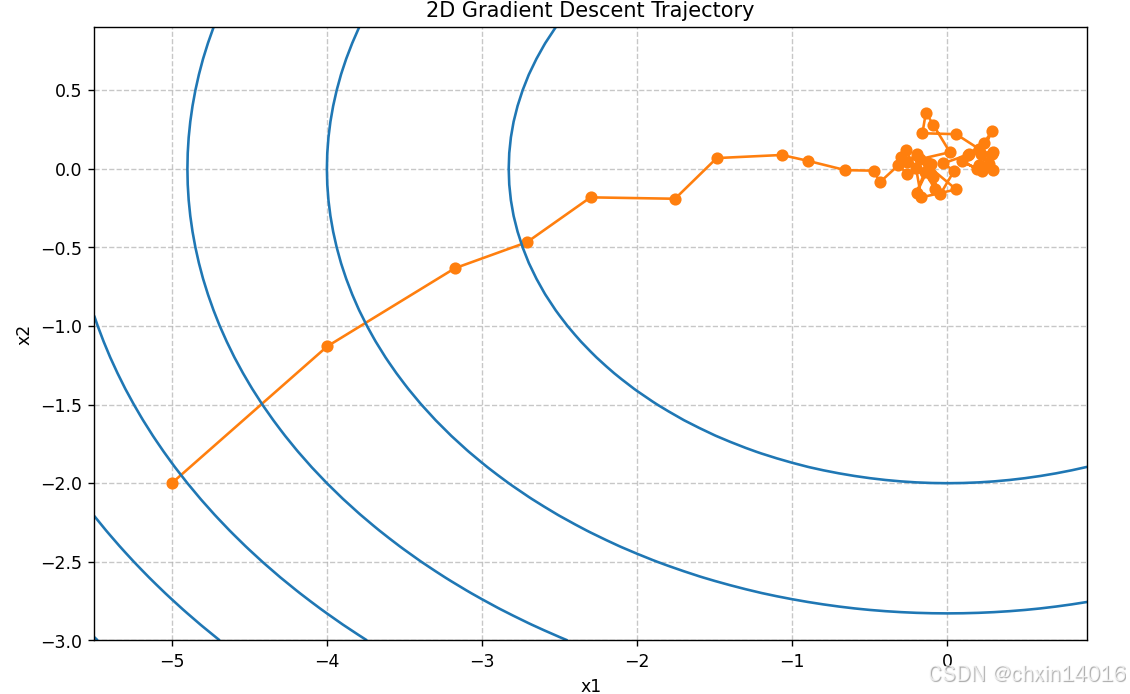
（3.2. 多元梯度下降）所演示的效果图

如图所示，随机梯度下降中变量的轨迹比在（3.2. 多元梯度下降）中观察到的梯度下降中观察到的轨迹嘈杂得多。这是由于梯度的随机性质。

  • 也就是说，即使我们接近最小值，我们仍然受到通过 的瞬间梯度所注入的不确定性的影响。
  • 即使经过50次迭代，质量仍然不那么好。甚至经过额外的步骤，仍没得到改善。
  • 这给我们留下了唯一的选择：改变学习率 η 。但是，
    • 若选择的学习率太小，则一开始就不会取得任何有意义的进展。
    • 若选择的学习率太大，将无法获得一个好的解决方案，如上所示。

解决这些相互冲突的目标的唯一方法是在优化过程中动态降低学习率。

这也是在sgd步长函数中添加学习率函数lr的原因。在上面的示例中，暂未启用学习率调度的任何功能，因为我们将相关的lr函数设置为常量。

4.2. 动态学习率 (随时间推移衰减)

用 与时间相关的学习率 取代 η 增加了控制优化算法收敛的复杂性。但是需要弄清 η 的衰减速度：

  • 若太快，则会将过早停止优化。
  • 若减少的太慢，则会在优化上浪费太多时间。

以下是随着时间推移调整 η 时使用的一些基本策略（稍后将讨论更高级的策略）：
使用 动态衰减的学习率

  • 分段常数 (piecewise constant)(常用实践)：
    • 在特定节点降低学习率(如 优化进度停顿时)，是训练深度网络的常见策略。
  • 指数衰减 (exponential decay)(谨慎使用)：
    • 衰减过快，可能会导致算法收敛之前过早停止，需格外小心。
  • 多项式衰减 (polynomial decay)(首选推荐)()：
    • 在凸优化的情况下，这种速率表现良好。(在理论和实践间取得了很好的平衡)
策略 核心思想 工作方式 优点 缺点 典型应用场景
​​1. 分段常数衰减​​ 在特定节点（如损失不再下降时）​​突然降低​​学习率。 根据阶段 （如第30、50个epoch） 将学习率降至一个新值 直观、简单、有效； 便于控制。 需要人工预设调整时机， 不够自适应。 ​​训练深度网络​​的常用策略， 当验证集损失进入平台期时使用。
​​2. 指数衰减​​ 学习率随训练步数 ​​连续、快速地衰减​​ 公式： η(t) = η₀ * e^(-λt) 其中 t是步数， 衰减速度由 λ控制 衰减平滑， 理论上有保证。 ​​衰减过快​​， 可能导致模型在收敛到良好解之前 就"过早停止"学习。 较少用于深度学习， 在某些理论推导或简单任务中可见。
​​3. 多项式衰减​​ 学习率随步数 ​​以相对缓慢的速度衰减​​ 公式： η(t) = η₀ * (1 + βt)^(-α) 其中 α=0.5是常见选择 ​​衰减速度适中​​， 既保证早期快速下降，又允许后期精细调优。​​ 理论上有保障​​，对于凸优化问题有良好的收敛性证明。 需要选择超参数 α和 β ​​理论研究和实践中都皆受欢迎， 尤其是在被证明是凸问题或近似凸的问题上。

指数衰减 实践演示：

python 复制代码 
def exponential_lr():
    ''' 指数学习率衰减策略
    学习率按 η = e^(-0.1*t)衰减
    调整指数系数（如-0.1）控制衰减速度
    衰减特点：
        初期下降较快（前几步学习率迅速减小）
        后期趋于平缓（当t较大时，e^(-0.1*t)接近0）
    适用场景：需要快速降低学习率的任务，但可能过早失去学习能力
    '''
    # 在函数外部定义，而在内部更新的全局变量
    global t  # 声明使用全局变量t
    t += 1    # 每次调用递增步数计数器
    return math.exp(-0.1 * t)  # 指数衰减公式: η = e^(-0.1*t)

# 初始化全局变量
t = 1                # 时间步计数器（从1开始）
lr = exponential_lr  # 设置学习率函数为指数衰减
common.show_trace_2d(f, common.train_2d(sgd, steps=1000, f_grad=f_grad))


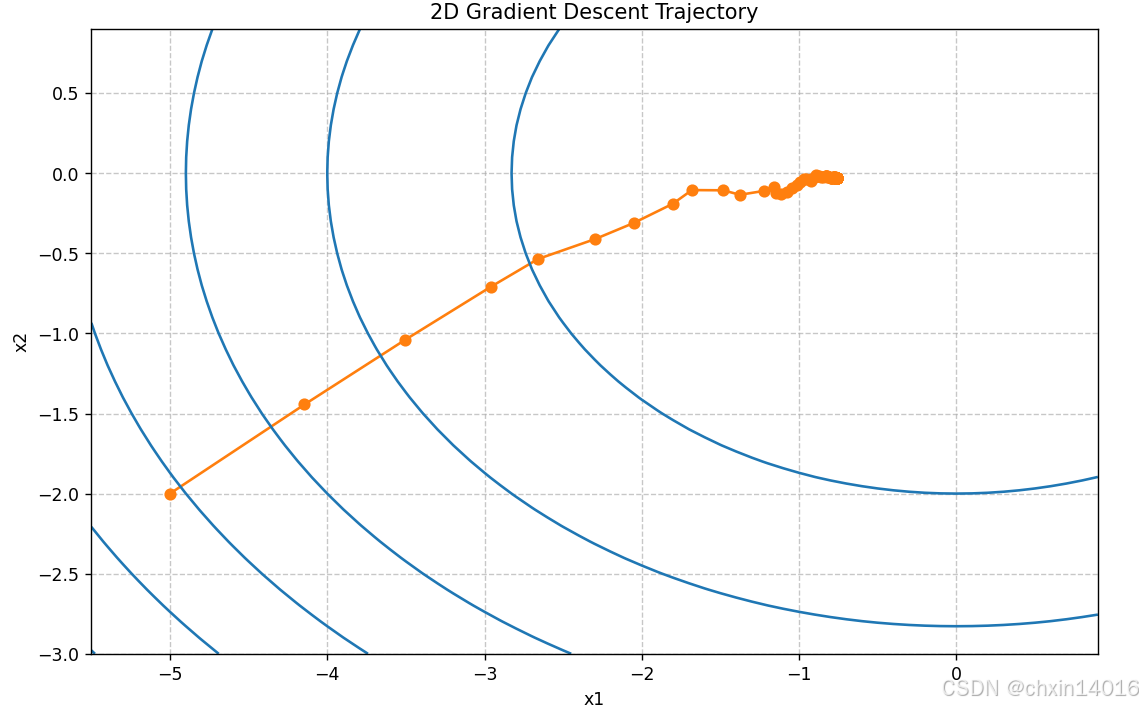指数衰减​：运行1000步展示长期衰减效果（学习率快速减小）

  • 正如预期的那样，参数的方差大大减少。但是，这是以未能收敛到最优解 为代价的。
  • 即使经过1000个迭代步骤，结果仍离最优解很远。事实上，该算法根本无法收敛。
  • 另一方面，若使用多项式衰减，其中学习率随迭代次数的平方根倒数衰减，那么仅在50次迭代之后，收敛就会更好。

多项式衰减 演示：

python 复制代码 
def polynomial_lr():
    ''' 多项式学习率衰减策略
    学习率按 η = (1 + 0.1*t)^(-0.5)衰减
    优先尝试 (1 + α*t)^(-0.5)，调整α
    衰减特点：
        初期下降平缓（保护早期快速学习能力）
        后期持续稳定衰减（避免后期震荡）
    理论保障：对于凸优化问题可证明收敛性
    参数选择：
        分母中的 0.1控制衰减速度
        指数 -0.5是理论推荐值
    '''
    # 在函数外部定义，而在内部更新的全局变量
    global t  # 声明使用全局变量t
    t += 1    # 每次调用递增步数计数器
    return (1 + 0.1 * t) ** (-0.5)  # 多项式衰减公式: η = (1+0.1*t)^(-0.5)

# 重新初始化全局变量
t = 1               # 重置时间步计数器（因为切换策略了）
lr = polynomial_lr  # 设置学习率函数为多项式衰减
common.show_trace_2d(f, common.train_2d(sgd, steps=50, f_grad=f_grad)) # 迭代次数降到50


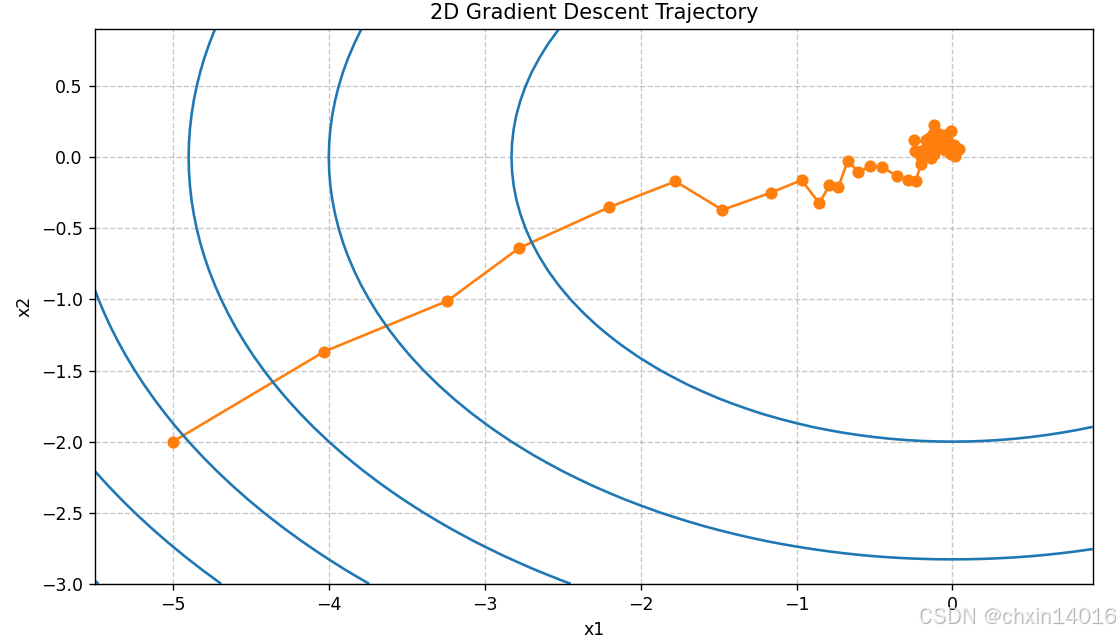​多项式衰减​：仅50步展示初期行为（学习率温和下降）

关于如何设置学习率，还有更多的选择。例如，

  • 先从较小的学习率开始，然后使其迅速上涨，再让它降低，尽管这会更慢。
  • 甚至可在较小和较大的学习率间切换。

现在，让我们专注于可以进行全面理论分析的学习率计划，即凸环境下的学习率。

  • 对于真实的神经网络(高度非凸)，我们​无法保证​ 训练算法能找到"最好"的解，只能期望找到一个"还不错"的解。
    • 因为总的来说，最大限度地减少非线性非凸问题是NP困难的。有关的研究调查，请参阅例如2015年Tibshirani的优秀讲义笔记。
    • ​NP困难"​ ：计算复杂性术语，意思是​从理论上讲，找到全局最优解的计算成本高得无法承受​，是所有现代计算机都无法在合理时间内解决的问题。

4.3. 凸目标的收敛性分析

（从​​理论​​上告知：只要函数凸且学习率设置得当，SGD就能收敛。它为我们使用SGD提供了信心和基本原则。）

  • 在满足一定条件时，随机梯度下降能够收敛到（或接近）最优解​。
  • 本章内容：从数学上证明以上观点。
    • 从数学上证明了SGD的有效性，
    • 并指出​成功收敛的关键在于使用一个适当衰减的学习率计划​。
    • 即 关键结论：学习率必须逐渐减小。

以下对凸目标函数的随机梯度下降的收敛性分析是可选读的，主要用于传达对问题的更多直觉。我们只限于最简单的证明之一 (Nesterov and Vial, 2000)。存在着明显更先进的证明技术，例如，当目标函数表现特别好时。

假设所有 的目标函数 在 中都是凸的。更具体地说，我们考虑随机梯度下降更新：

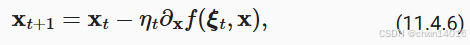
其中 是训练样本 的目标函数： 从第 t 步的某个分布中提取， 是模型参数。用以下公式(11.4.7) 表示期望风险：

表示对于 的最低风险。最后让 表示最小值（我们假设它存在于定义 的域中）。在这种情况下，我们可以跟踪时间 t 处的当前参数 和风险最小化器 之间的距离，看看它是否随着时间的推移而改善：

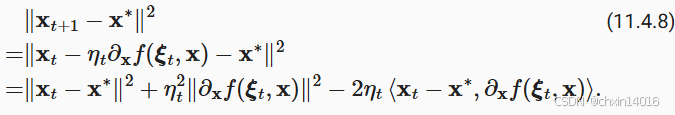
我们假设随机梯度 的 L2范数受到某个常数 的限制，因此我们有

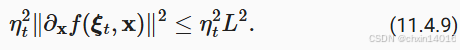
我们最感兴趣的是 和 之间的距离如何变化的期望 。事实上，对于任何具体的步骤序列，距离可能会增加，这取决于我们遇到的 。因此我们需要点积的边界。因为对于任何凸函数 ，所有 和 都满足 ，按凸性我们有

将不等式 (11.4.9)和 (11.4.10)代入 (11.4.8)我们在时间 t + 1 时获得参数之间距离的边界，如下所示：

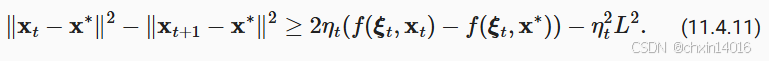
这意味着，只要当前损失和最优损失之间的差异超过 ，我们就会取得进展。由于这种差异必然会收敛到零，因此学习率 也需要消失。

接下来，我们根据 (11.4.11)取期望。得到

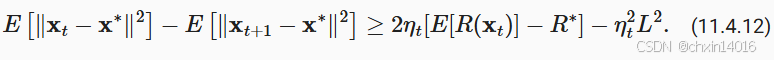
最后一步是对 的不等式求和。在求和过程中抵消中间项，然后舍去低阶项，可以得到

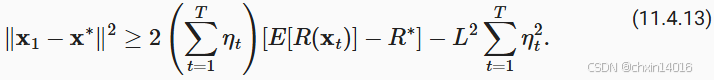
请注意，我们利用了给定的 ，因而可以去掉期望。最后定义

因为有

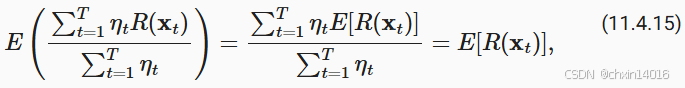
根据詹森不等式（令 (11.2.3)中 i = t ， ）和 的凸性使其满足的 ，因此，

将其代入不等式 (11.4.13)得到边界

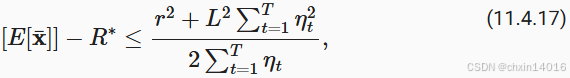
其中 是初始选择参数与最终结果之间距离的边界。简而言之，收敛速度取决于随机梯度标准的限制方式（）以及初始参数值与最优结果的距离（）。请注意，边界由 而不是 表示。因为 是优化路径的平滑版本。只要知道 和 ，我们就可以选择学习率 。这个就是上界 。也就是说，我们将按照速度 收敛到最优解。

4.4. 随机梯度和有限样本

（从​​实践​ ​角度说明：实际采用的​​无放回小批量抽样​​方式是一种更高效、更常用的策略。）

在实际操作中，从数据集中 获取"随机梯度"的 两种抽样方式：

  • 有放回抽样​ ：
    • 操作：从一副扑克牌中随机抽一张，记录后​放回牌堆​，再抽下一张。
    • 效果：同一张牌可能在同一次训练周期（epoch）内被多次抽到。
  • 无放回抽样​ ：(通常更优) (深度学习默认使用)
    • 操作：洗牌后依次发牌​ ，保证训练集中的每个样本在一个epoch内​都被使用一次，且仅一次​。
    • 实现方式：
      • 通常通过将数据集随机打乱(shuffle)后分成一个个小批量(mini-batch)来实现。
      • 即 打乱数据后按小批量训练。

无放回抽样通常优于有放回抽样​​。

  • ​方差更小​ ：
    • 无放回抽样：能确保在一个epoch内更"均匀"地使用所有数据，计算出的梯度估计​更稳定（方差更小）​。
    • 有放回抽样：可能因为某些样本被重复抽到而引入更大的随机性。
  • ​收敛更快​：梯度估计更稳定意味着优化路径更平滑，往往能带来更快的收敛速度。

到目前为止，在谈论随机梯度下降时，我们进行得有点快而松散。我们假设从分布 中采样得到样本 （通常带有标签 ），并且用它来以某种方式更新模型参数。特别是，对于有限的样本数量，我们仅仅讨论了由某些允许我们在其上执行随机梯度下降的函数 和 组成的离散分布 。

但是，这不是我们真正做的。在本节的简单示例中，我们只是将噪声添加到其他非随机梯度上，也就是说，我们假装有成对的 。事实证明，这种做法在这里是合理的（有关详细讨论，请参阅练习）。更麻烦的是，在以前的所有讨论中，我们显然没有这样做。相反，我们遍历了所有实例恰好一次 。要了解为什么这更可取，可以反向考虑一下，即我们有替换地 从离散分布中采样 n 个观测值。随机选择一个元素 i 的概率是 1/n 。因此选择它至少一次就是

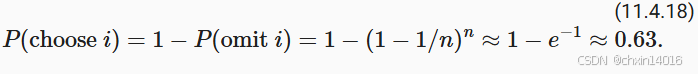
类似的推理表明，挑选一些样本（即训练示例）恰好一次的概率是

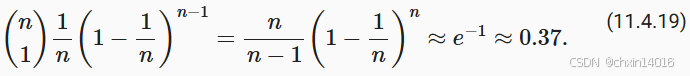
这导致与无替换 采样相比，方差增加并且数据效率降低。因此，在实践中我们执行后者（这是本书中的默认选择）。最后一点注意，重复采用训练数据集的时候，会以不同的随机顺序遍历它。

小结

  • 对于凸问题，我们可以证明，对于广泛的学习率选择，随机梯度下降将收敛到最优解。

  • 对于深度学习而言，情况通常并非如此。但是，对凸问题的分析有助于深入了解如何进行优化，即逐步降低学习率，尽管不是太快。

  • 若学习率太小或太大，就会出现问题。实际上，通常只有经过多次实验后才能找到合适的学习率。

  • 当训练数据集中有更多样本时：

    • 计算梯度下降的每次迭代的代价更高

    • 因此这时候首选 随机梯度下降

  • 随机梯度下降的最优性保证在非凸情况下一般不可用，因为需要检查的局部最小值的数量可能是指数级的。

5. 小批量随机梯度下降

到目前为止，我们在基于梯度的学习方法中遇到了两个极端情况：

  • （3. 梯度下降）：使用完整数据集来计算梯度并更新参数
  • （4. 随机梯度下降）：一次处理一个训练样本来取得进展

二者各有利弊：

  • 每当数据非常相似时，梯度下降并不是非常"数据高效"。
  • 而由于CPU和GPU无法充分利用向量化，随机梯度下降并不特别"计算高效"。
  • 这暗示了两者之间可能有折中方案，这便涉及到小批量随机梯度下降（minibatch gradient descent）。

5.1. 向量化和缓存

深度学习使用小批量（mini-batch）计算​​，而非

  • 逐样本（batch_size=1）或
  • 全批量（batch_size=整个数据集）

关键在于​​计算效率的优化​ ​，尤其是​​内存带宽与计算能力的平衡​​。

性能对比示例假设：

  • 计算一个样本的前向传播需要1μs
  • Python调用框架开销为10μs
批量大小 总计算时间 有效计算占比
1 10 + 1 = 11μs 9%
128 10 + 128 = 138μs 93%

小批量计算 对（硬件层面的关键矛盾​）解决方式如下 ↓

通过​​数据局部性（data locality）​​优化：

使用小批量的决策的核心是计算效率。 当考虑与多个GPU和多台服务器并行处理时，这一点最容易被理解。在这种情况下，我们需要向每个GPU发送至少一张图像。 有了每台服务器8个GPU和16台服务器，我们就能得到大小为128的小批量。

（内存层级与带宽瓶颈）

当涉及到单个GPU甚至CPU时，事情会更微妙一些： 这些设备有多种类型的内存、通常情况下多种类型的计算单元以及在它们之间不同的带宽限制。 例如，

  • 一个CPU有少量寄存器（register），L1和L2缓存，以及L3缓存（在不同的处理器内核之间共享）。
  • 随着缓存的大小的增加，它们的延迟也在增加，同时带宽在减少。
    • 计算单元直接从寄存器/L1缓存读取数据时速度最快
    • 若数据不在缓存中（cache miss），需从主内存加载，等待时间≈计算100次浮点运算
  • 可以说，处理器能够执行的操作远比主内存接口所能提供的多得多。
存储类型 容量 延迟 带宽 典型用途
​​寄存器​​ ~1KB 0.5ns 极高 当前计算的临时变量
​​L1缓存​​ ~32KB 1ns 高 高频访问数据
​​L2缓存​​ ~256KB 3ns 中 次级高频数据
​​L3缓存​​ ~50MB 10ns 较低 多核共享数据
​​主内存​​ >16GB 100ns 低 所有数据存储

（硬件层面的关键矛盾​）

现代计算设备存在一个根本性矛盾：

  • 1、计算单元（CPU/GPU）的速度极快​
    • 例如：具有16个内核 和 AVX-512向量化的2GHz CPU每秒可处理高达 个字节 (次浮点运算)。
    • 同时，GPU的性能很容易超过该数字100倍，即 GPU算力可达CPU的100倍以上。
  • 2、​内存带宽严重不足
    • 中端服务器处理器的带宽 通常不超过100Gb/s，即不到处理器满负荷所需的十分之一。 更糟糕的是，并非所有的内存入口都是相等的：内存接口通常为64位或更宽（例如，在最多384位的GPU上）。
    • 因此读取单个字节会导致由于更宽的存取而产生的代价。即 读取单个字节可能需要搬运64位（8字节）或更宽的数据块。
  • 结果​：处理器经常"饿着等数据"，大部分时间花在等待数据从内存加载到缓存/寄存器。

（矩阵乘法的优化策略）

其次，第一次存取的额外开销很大，而按序存取（sequential access）或突发读取（burst read）相对开销较小。 有关更深入的讨论，请参阅此维基百科文章。

减轻这些限制的方法是使用足够快的CPU缓存层次结构来为处理器提供数据。 这是深度学习中批量处理背后的推动力。

举一个简单的例子：矩阵-矩阵乘法。 比如 A=BC ，我们有很多方法来计算 A 。例如以下四种：

| 计算方式 | 内存访问次数 | 缓存利用率 | 适合场景 |
| ​​逐元素计算​ ​（） | O(mnp) | 极低 | 不推荐 |
| ​​逐列计算​ ​（） | O(mp) | 中等 | 小规模数据 |
| 简单地计算 | / | / | / |

​​分块计算​​（将A,B分块后计算） O(mp/block_size) 高 ​​深度学习常用​
  • ① 逐元素计算（）：通过点积进行逐元素计算
    • 每次计算一个元素 时，都需要将一行和一列向量复制到CPU中。
    • 更糟糕的是，由于矩阵元素是按顺序对齐的，因此当从内存中读取它们时，需要访问两个向量中许多不相交的位置。
  • ② 逐列计算（）：一次计算一列。同样，可以一次计算 A 一行
    • 相对更有利。能在遍历 B 的同时，将列向量 保留在CPU缓存中。
    • 它将内存带宽需求减半，相应地提高了访问速度。
  • ③ 简单地计算 ：表面上是最可取的，然而大多数矩阵可能不能完全放入缓存中。
  • ④ 分块计算（将A,B分块后计算）：将 B 和 C 分成较小的区块矩阵，然后一次计算 A 的一个区块
    • 提供了一个实践上很有用的方案，可以将矩阵的区块移到缓存中然后在本地将它们相乘。

分块计算示例：

将A,B分为16×16的块，每次计算：

  1. 将A和B的当前块加载到 L1缓存
  2. 计算该块的所有乘积（256次浮点运算复用同一批数据）
  3. 写回结果到C的对应块

除了计算效率之外，Python和深度学习框架本身带来的额外开销也是相当大的。

  • 回想一下，每次执行代码时，Python解释器都会向深度学习框架发送一个命令，要求将其插入到计算图中并在调度过程中处理它。这样的额外开销可能是非常不利的。
  • 总而言之，最好用向量化（和矩阵）。
python 复制代码 
# %matplotlib inline
import numpy as np
import torch
import common
from torch import nn

timer = common.Timer()      # 初始化计时器
A = torch.zeros(256, 256)   # A: 256x256零矩阵（用于存储结果）
B = torch.randn(256, 256)   # B: 256x256随机矩阵
C = torch.randn(256, 256)   # C: 256x256随机矩阵

【逐元素计算】：即 按元素分配。遍历 B的行 和 C的列，计算点积后将值分配给 A 。

python 复制代码 
# 测试一：【逐元素】计算A=BC
timer.start()   # 开始计时
for i in range(256):      # 遍历行
    for j in range(256):  # 遍历列
        # 计算 B的第i行 与 C的第j列 的点积
        A[i, j] = torch.dot(B[i, :], C[:, j])
stop_time = timer.stop()    # 停止计时
print(f"【逐元素】计算耗时：{stop_time}")

【逐列计算】：执行按列分配，比逐元素计算更快。

python 复制代码 
# 测试二：【逐列】计算A=BC
timer.start()
for j in range(256):  # 仅遍历列
    # 计算B与C的第j列的矩阵-向量乘积
    A[:, j] = torch.mv(B, C[:, j])  # mv = matrix-vector multiplication
stop_time = timer.stop()
print(f"【逐列】计算耗时：{stop_time}")

【分块计算】：是最有效的方法。在一个区块中执行整个操作。

  • 在深度学习和科学计算中，​完整的矩阵乘法（如 torch.mm或 A = B @ C），就是经过高度优化的分块计算，而​ 不是简单的逐元素计算。

下面看看它们各自的操作速度是多少。

python 复制代码 
# 测试三：【一次性】计算A=BC （一次性完整矩阵乘法）
timer.start()
# 直接调用优化后的矩阵乘法
A = torch.mm(B, C)  # mm = matrix-matrix multiplication
stop_time = timer.stop()
print(f"【一次性完整矩阵乘法】计算耗时：{stop_time}")

计算三种方法的GigaFLOPs：（性能对比）

python 复制代码 
min_time = 1e-6  # 1微秒下限(避免除以零，增加最小时间阈值)

# 乘法和加法作为单独的操作（在实践中融合）即
# 底层计算库(如BLAS、cuBLAS)会将矩阵乘法(GEMM) 和
# 后续的加法操作（如偏置项相加）合并为一个复合操作，从而显著提升计算效率
gigaflops = [2/max(i, min_time) for i in timer.times]
print(f'performance in Gigaflops 性能对比（GFLOPS）: \n'
      f'element 逐元素计算: {gigaflops[0]:.3f}, \n'
      f'column 逐列计算 : {gigaflops[1]:.3f}, \n'
      f'full 完整矩阵乘法: {gigaflops[2]:.3f}\n')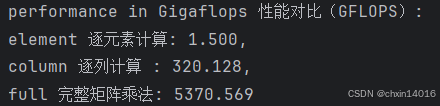
方法 内存访问模式 缓存利用率 框架优化
逐元素 每次访问不连续的行和列 最差 无
逐列 按列连续访问 中等 部分
完整矩阵乘法 分块访问 最高 完全优化
  • 在深度学习和科学计算中，​完整的矩阵乘法（如 torch.mm或 A = B @ C）并不是简单的逐元素计算，而是经过高度优化的分块计算​。

5.2. 小批量

之所以 读取数据的小批量，而非观测单个数据来更新参数：

  • 处理单个观测值需要执行许多单一矩阵-矢量（甚至矢量-矢量）乘法，这耗费很大，且对应深度学习框架也要巨大的开销。
  • 这既适用于计算梯度以更新参数时，也适用于用神经网络预测。
  • 也就是说，每当执行 时，消耗巨大。其中

我们可以通过将其应用于一个小批量观测值来提高此操作的计算效率。也就是说，将梯度替换为一个小批量而非单个观测值
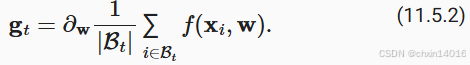每次迭代随机采样一个批量 B

下面看看这对 的统计属性 产生的影响：

  • 由于 和小批量 的所有元素都是从训练集中随机抽出的，因此梯度的期望保持不变。另一方面，方差显著降低。
  • 由于小批量梯度由正在被平均计算的 个独立梯度组成，其标准差降低了 。 这本身就是一件好事，因为这意味着更新与完整的梯度更接近了。

批量大小的选择原则

  1. ​GPU并行​：选择2的幂次方（如32/64/128）以适配硬件
  2. ​内存限制​：最大不超过显存容量
  3. 经验公式​ ：

直观来说，这表明选择大型的小批量 将是普遍可行的。 然而，经过一段时间后，与计算代价的线性增长相比，标准差的额外减少是微乎其微的。 在实践中选择 一个足够大的小批量 ，可提供良好的计算效率同时仍适合GPU的内存。下面，我们来看看这些高效的代码。 在里面执行相同的矩阵-矩阵乘法，但是这次将其一次性分为64列的"小批量"：

python 复制代码 
timer.start()
for j in range(0, 256, 64): # 一次性分为64列的"小批量"
    A[:, j:j+64] = torch.mm(B, C[:, j:j+64])
timer.stop()
print(f'performance in Gigaflops: block {2 / timer.times[3]:.3f}')

显而易见，小批量上的计算基本上与完整矩阵一样有效。

5.3. 读取数据集

开始演示如何从数据中有效地生成小批量。

  • 下面使用NASA开发的测试机翼的数据集不同飞行器产生的噪声来比较这些优化算法。
  • 为方便起见，只使用前1500样本。
  • 数据已作预处理：我们移除了均值并将方差重新缩放到每个坐标为1。
python 复制代码 
# 下载器与数据集配置
# 为 time_machine 数据集注册下载信息，包括文件路径和校验哈希值（用于验证文件完整性）
downloader = common.C_Downloader()
DATA_HUB = downloader.DATA_HUB  # 字典，存储数据集名称与下载信息
DATA_URL = downloader.DATA_URL  # 基础URL，指向数据集的存储位置

DATA_HUB['airfoil'] = (DATA_URL + 'airfoil_self_noise.dat',
                           '76e5be1548fd8222e5074cf0faae75edff8cf93f')
python 复制代码 
def get_data_ch11(downloader, batch_size=10, n=1500):
    ''' 数据集加载并预处理：不同飞行器产生的噪音'''
    # 从CSV加载空气动力学数据集（制表符分隔）
    data = np.genfromtxt(downloader.download('airfoil'),
                         dtype=np.float32, delimiter='\t')
    # 数据标准化：每个特征减去均值除以标准差，并转tensor
    data = torch.from_numpy((data - data.mean(axis=0)) / data.std(axis=0))
    # 创建数据迭代器（特征+标签）：前n条样本，最后一列作为标签
    # load_array返回DataLoader对象
    data_iter = load_array((data[:n, :-1], data[:n, -1]),
                               batch_size, is_train=True)
    return data_iter, data.shape[1]-1  # 返回迭代器和特征维度（总列数-1）

5.4. 从零开始实现

（线性回归实现 & softmax回归实现------ 动手学深度学习3.2~3.7_自己动手写线性回归-CSDN博客的 线性回归的从零开始实现）中已经实现过小批量随机梯度下降算法。

  • 这里将它的输入参数变得更加通用，主要是为了方便本章后面介绍的其他优化算法也可以使用同样的输入。具体来说：
    • 添加了一个状态输入states，并将超参数放在字典hyperparams中。
    • 此外，将在训练函数里对各个小批量样本的损失求平均，因此优化算法中的梯度不需要除以批量大小。
python 复制代码 
def sgd(params, states, hyperparams):
    '''sgd优化器
    params：需要被优化的变量列表（模型参数列表）
    states：状态
    hyperparams：存放超参数的字典
    '''
    for p in params:
        # .sub_() 原地减法操作，直接修改参数值
        # 等效于 p.data = p.data - η·∇L，但更高效
        p.data.sub_(hyperparams['lr'] * p.grad) # 参数更新
        p.grad.data.zero_() # 梯度清零

p.data ：

  • ​p​ 是 torch.Tensor，可能带有梯度计算信息（requires_grad=True）
  • p.data​ 是纯数值张量，直接修改它不会影响梯度计算图

p.data.sub_(hyperparams['lr'] * p.grad) ：

  • 等效于 p.data = p.data - η·∇L，但更高效

  • .sub_() 原地减法操作，直接修改参数值

    • 下划线 _​ 表示原地操作（in-place operation），直接修改原数据

    • 对比：

      python 复制代码 
      # 下划线 _​​ 表示原地操作（in-place operation），直接修改原数据

# 非原地操作（生成新Tensor）
p.data = p.data - lr * p.grad  # 低效，分配新内存

# 原地操作（推荐）
p.data.sub_(lr * p.grad)       # 高效，直接修改原数据

  • 这句其实就是进行参数更新：如

    • 更新规则（SGD）：

    • 对应代码：

      python 复制代码 
      w.data.sub_(lr * w.grad)  # w -= lr * grad_w
b.data.sub_(lr * b.grad)  # b -= lr * grad_b

下面实现一个通用的训练函数，以方便本章后面介绍的其他优化算法使用：

  • 初始化一个线性回归模型，
  • 然后可以使用小批量随机梯度下降 以及后续小节介绍的其他算法来训练模型。
python 复制代码 
# 定义模型
def linreg(X, w, b):
    """线性回归模型"""
    return torch.matmul(X, w) + b

# 定义损失函数
def squared_loss(y_hat, y):  # y_hat预测值, y真实值
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2 # /2只是为了与导数的因子2抵消，即为了导数计算更简洁

# 对模型进行训练和测试
def evaluate_loss(net, data_iter, loss):  #@save
    """评估给定数据集上模型的损失"""
    metric = Accumulator(2)  # 损失的总和,样本数量
    for X, y in data_iter:
        out = net(X)             # 模型预测输出结果
        y = y.reshape(out.shape) # 将实际标签y的形状调整为与模型输出out一致
        l = loss(out, y)         # 模型输出out与实际标签y之间的损失
        metric.add(l.sum(), l.numel()) # 将损失总和 和 样本总数 累加到metric中
    return metric[0] / metric[1] # 损失总和/预测总数，即平均损失
python 复制代码 
def train_ch11(trainer_fn, states, hyperparams, data_iter,
               feature_dim, num_epochs=2):
    ''' 通用训练函数，支持不同的优化器（如SGD、Adam）
    trainer_fn  ：优化器函数（如sgd）
    states      ：优化器状态（如动量、二阶矩估计）
    hyperparams ：超参数字典（如学习率lr）
    data_iter   ：数据迭代器（生成(X, y)批次）
    feature_dim ：输入特征维度
    num_epochs  ：训练轮数（默认2轮）
    '''
    # 初始化模型参数（正态分布权重，零初始化偏置）
    w = torch.normal(mean=0.0, std=0.01, size=(feature_dim, 1), requires_grad=True)
    b = torch.zeros((1), requires_grad=True)

    # 定义模型和损失函数
    net = lambda X: linreg(X, w, b) # 线性回归模型
    loss = squared_loss             # 平方损失函数

    # 训练模型
    animator = Animator(xlabel='epoch', ylabel='loss',
                            xlim=[0, num_epochs], ylim=[0.22, 0.35])
    n, timer = 0, Timer() # 样本计数器，计时器
    for _ in range(num_epochs):
        for X, y in data_iter:
            l = loss(net(X), y).mean()  # 前向传播计算平均损失
            l.backward()                # 反向传播计算梯度
            # 优化器更新参数（传入参数列表、状态字典和超参数）
            trainer_fn([w, b], states, hyperparams) # 优化器更新参数
            # （梯度清零在优化器中实现）
            n += X.shape[0]  # 更新样本计数
            if n % 200 == 0: # 每200样本记录一次损失
                timer.stop()
                # 添加记录点：当前迭代次数，验证集损失
                animator.add(n/X.shape[0]/len(data_iter),
                             (evaluate_loss(net, data_iter, loss),))
                timer.start()
    print(f'loss: {animator.Y[0][-1]:.3f}, {timer.avg():.3f} sec/epoch')
    return timer.cumsum(), animator.Y[0] # 返回总耗时和损失曲线

下面来看批量梯度下降的优化是如何进行的：

  • 可以通过将小批量设置为1500（即样本总数）来实现。
  • 因此，模型参数每个迭代轮数只迭代一次。
python 复制代码 
# 训练流程封装
def train_sgd(lr, batch_size, num_epochs=2):
    '''训练流程封装：入口函数
    1、初始化训练参数：如学习率，批量大小，训练轮数，所用优化器(sgd)
    2、启动训练流程
    '''
    # 获取数据迭代器和特征维度
    data_iter, feature_dim = common.get_data_ch11(downloader, batch_size)
    # 启动训练流程
    return common.train_ch11(
        sgd, None, {'lr': lr}, data_iter, feature_dim, num_epochs)

# 执行训练：
''' 全批量梯度下降(GD)，每1500样本更新一次
lr=1：大学习率（全批量梯度更稳定，允许大学习率）
batch_size=1500 ：全批量（使用全部数据计算梯度）
num_epochs=10   ：训练10轮
行为：
    每轮（epoch）计算所有1500个样本的平均梯度，更新一次参数。
    共更新 10次（每轮1次）
'''
# 学习率1，批量大小1500，训练轮数10
gd_res = train_sgd(1, 1500, 10)
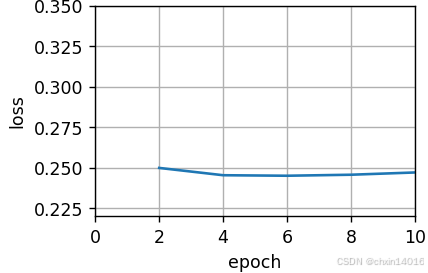
  • 批量大小为1500（全批量梯度下降，GD）如上 ↑
  • 批量大小为1（随机梯度下降，SGD ）如下 ↓
    • 这里选择了很小的学习率，以简化实现。
      • SGD的梯度噪声大​ （因为每次只用一个样本），所以需要 ​更小的学习率​ 避免震荡。
      • 例如​ ：批量GD可以用 lr=0.1，但SGD可能需要 lr=0.01甚至更小。
    • 在随机梯度下降的实验中，每当一个样本被处理，模型参数都会更新。
      • ​SGD的特点​：每看一个样本就更新一次参数
      • 对比批量GD​：每看完整批（如1500个样本）才更新一次
    • 在该例子中，这相当于每个迭代轮数有1500次更新。
      • 数据集大小=1500
      • ​SGD​ ：每轮（epoch）遍历所有样本，每个样本单独更新一次 → ​1500次更新/轮
      • ​批量GD​ ：每轮计算所有样本的平均梯度 → ​1次更新/轮​
  • 效果：目标函数值的下降在1个迭代轮数后就变得较为平缓。
    • SGD的收敛曲线：​
      • 初期下降快（因频繁更新）
      • 后期波动小（因学习率小，接近收敛）
    • **批量GD的收敛曲线：**每次更新方向更准确，但更新次数少。

尽管两个例子在一个迭代轮数内都处理了1500个样本，但实验中随机梯度下降的一个迭代轮数耗时更多。

方法 梯度计算次数 / 轮 参数更新次数 / 轮 每轮耗时 收敛曲线
​​SGD​​ 1500 1500 高
​​批量GD​​ 1500 1 低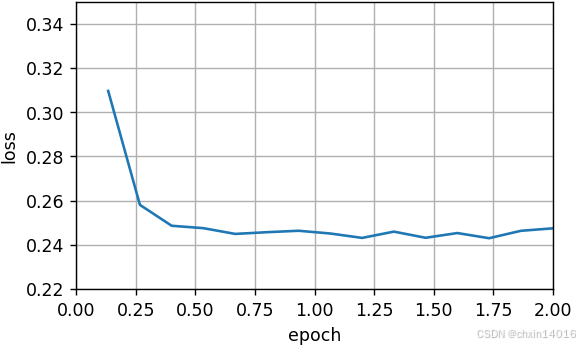

因为随机梯度下降更频繁地更新了参数，且一次处理单个观测值效率较低。

python 复制代码 
''' 随机梯度下降(SGD)，每个样本更新一次
lr=0.005：极小学习率（单样本梯度噪声大，需小步长）
batch_size=1：纯SGD（每个样本单独更新）
num_epochs=2（默认值）
行为：
    每轮（epoch）遍历1500个样本，每个样本更新一次参数。
    共更新 1500 × 2 = 3000次（每轮1500次，迭代次数默认=2）
'''
sgd_res = train_sgd(0.005, 1)

最后，当批量大小等于100时，使用小批量随机梯度下降进行优化。

  • 每个迭代轮数所需的时间：比 随机梯度下降 和 批量梯度下降 所需的时间短。
python 复制代码 
''' 小批量梯度下降（Mini-batch）
每轮更新次数 分别为：
15次/轮（1500/100）
150次/轮（1500/10）
但实际只更新了默认2轮(为了快速验证)，所以实际总更新次数如下：
15 × 2 = 30
150 × 2 = 300
'''
mini1_res = train_sgd(.4, 100) # 中等批量

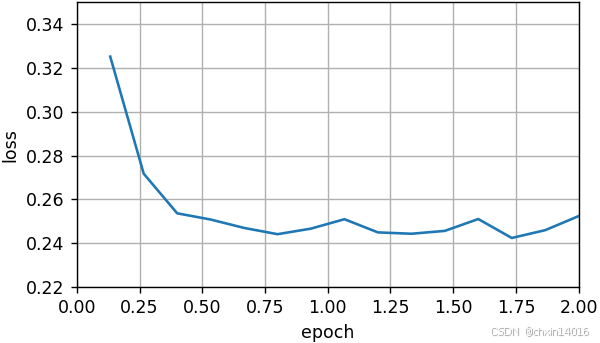
将批量大小减少到10，每个迭代轮数的时间都会增加，因为每批工作负载的执行效率变得更低。

python 复制代码 
mini2_res = train_sgd(.05, 10) # 小批量

现在可以比较前四个实验的时间与损失。可以看出，

  • 尽管在处理的样本数方面，随机梯度下降的收敛速度快于梯度下降，但与梯度下降相比，它需要更多的时间来达到同样的损失，因为逐个样本来计算梯度并不那么有效。
  • 小批量随机梯度下降能够平衡收敛速度和计算效率。
    • 大小为10的小批量比随机梯度下降更有效；
    • 大小为100的小批量在运行时间上甚至优于梯度下降。
python 复制代码 
# zip() 将时间序列和损失序列分离。将所有 时间序列和损失序列 分别整合成元组
#       元组内每个元素为 某种梯度下降法的 时间序列 或 损失序列
# map(list, ...) 将zip生成的元组转换为列表(将 转列表 应用到每个zip生成的元组上)
# *list() 将嵌套列表解包为独立参数(相当于4种梯度下降法的 时间序列/损失序列 都单独拎出来，而不是大的时间序列整体)
common.plot(*list(map(list, zip(gd_res, sgd_res, mini1_res, mini2_res))),
         'time (sec)', 'loss',
            xlim=[1e-2, 10], # 时间轴范围（0.01~10秒）
            xscale='log',    # 时间轴用对数坐标（便于观察初期快速下降）
            figsize=[6, 3],
            legend=['gd', 'sgd', 'batch size=100', 'batch size=10'])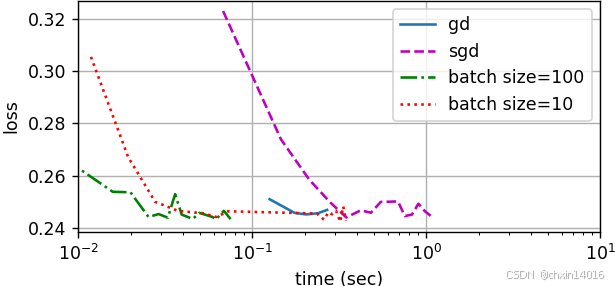

批量大小 vs. 学习率​

  • 大批量（如1500）​ ：
    • 梯度估计更准确 → 可用​大学习率​ （如lr=1）
    • 更新次数少 → ​收敛慢但稳定​
  • ​小批量（如10）​ ：
    • 梯度噪声大 → 需​小学习率​ （如lr=0.05）
    • 更新次数多 → ​收敛快但波动大​
  • 单样本（SGD）
    • 梯度噪声极大 → ​极小学习率​ （如lr=0.005）
    • 更新极频繁 → ​计算效率低​

时间消耗​

  • SGD最慢​：每轮1500次反向传播和更新（GPU并行利用率低）
  • ​全批量GD最快​：每轮1次大规模并行计算（充分利用GPU）

总结：

  1. 全批量GD​：稳定但慢，适合小数据集
  2. ​纯SGD​：收敛快但噪声大，效率低
  3. 小批量（100）​：平衡速度和稳定性
  4. 小批量（10）​：更接近SGD，但效率稍高

【此处开始往后未整理】5.5. 简洁实现

下面用深度学习框架自带算法实现一个通用的训练函数，并在本章中其它小节使用它：

python 复制代码 
#@save
def train_concise_ch11(trainer_fn, hyperparams, data_iter, num_epochs=4):
    # 初始化模型
    net = nn.Sequential(nn.Linear(5, 1))
    def init_weights(m):
        if type(m) == nn.Linear:
            torch.nn.init.normal_(m.weight, std=0.01)
    net.apply(init_weights)

    optimizer = trainer_fn(net.parameters(), **hyperparams)
    loss = nn.MSELoss(reduction='none')
    animator = d2l.Animator(xlabel='epoch', ylabel='loss',
                            xlim=[0, num_epochs], ylim=[0.22, 0.35])
    n, timer = 0, d2l.Timer()
    for _ in range(num_epochs):
        for X, y in data_iter:
            optimizer.zero_grad()
            out = net(X)
            y = y.reshape(out.shape)
            l = loss(out, y)
            l.mean().backward()
            optimizer.step()
            n += X.shape[0]
            if n % 200 == 0:
                timer.stop()
                # MSELoss计算平方误差时不带系数1/2
                animator.add(n/X.shape[0]/len(data_iter),
                             (d2l.evaluate_loss(net, data_iter, loss) / 2,))
                timer.start()
    print(f'loss: {animator.Y[0][-1]:.3f}, {timer.avg():.3f} sec/epoch')

下面使用这个训练函数，复现之前的实验。

python 复制代码 
data_iter, _ = get_data_ch11(10)
trainer = torch.optim.SGD
train_concise_ch11(trainer, {'lr': 0.01}, data_iter)

小结

  • 由于减少了深度学习框架的额外开销，使用更好的内存定位以及CPU和GPU上的缓存，向量化使代码更加高效。

  • 随机梯度下降的"统计效率"与大批量一次处理数据的"计算效率"之间存在权衡。

    • 小批量随机梯度下降提供了两全其美的答案：计算和统计效率。

  • 在小批量随机梯度下降中，我们处理通过训练数据的随机排列获得的批量数据（即每个观测值只处理一次，但按随机顺序）。

  • 在训练期间降低学习率有助于训练。

  • 一般来说，小批量随机梯度下降比随机梯度下降和梯度下降的速度快，收敛风险较小。

6. 动量法

在（4. 随机梯度下降）中，我们详述了如何执行随机梯度下降，即在只有嘈杂的梯度可用的情况下执行优化时会发生什么。 对于嘈杂的梯度，我们在选择学习率需要格外谨慎。 如果衰减速度太快，收敛就会停滞。 相反，如果太宽松，我们可能无法收敛到最优解。

6.1. 基础

6.1.1. 泄漏平均值

上一节中我们讨论了小批量随机梯度下降作为加速计算的手段。 它也有很好的副作用，即平均梯度减小了方差。 小批量随机梯度下降可以通过以下方式计算：

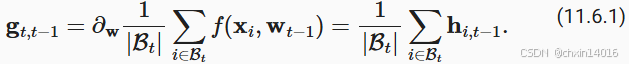
为了保持记法简单，在这里我们使用 作为样本 i 的随机梯度下降，使用时间 t - 1 时更新的权重 t - 1 。 如果我们能够从方差减少的影响中受益，甚至超过小批量上的梯度平均值，那很不错。 完成这项任务的一种选择是用泄漏平均值（leaky average）取代梯度计算：

其中 。 这有效地将瞬时梯度替换为多个"过去"梯度的平均值。 被称为动量 （momentum）， 它累加了过去的梯度。 为了更详细地解释，让我们递归地将 扩展到

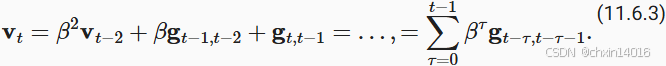
其中，较大的 相当于长期平均值，而较小的 相对于梯度法只是略有修正。 新的梯度替换不再指向特定实例下降最陡的方向，而是指向过去梯度的加权平均值的方向。 这使我们能够实现对单批量计算平均值的大部分好处，而不产生实际计算其梯度的代价。

上述推理构成了"加速"梯度方法的基础，例如具有动量的梯度。 在优化问题条件不佳的情况下（例如，有些方向的进展比其他方向慢得多，类似狭窄的峡谷），"加速"梯度还额外享受更有效的好处。 此外，它们允许我们对随后的梯度计算平均值，以获得更稳定的下降方向。 诚然，即使是对于无噪声凸问题，加速度这方面也是动量如此起效的关键原因之一。

正如人们所期望的，由于其功效，动量是深度学习及其后优化中一个深入研究的主题。 例如，请参阅文章，观看深入分析和互动动画。 动量是由 (Polyak, 1964)提出的。 (Nesterov, 2018)在凸优化的背景下进行了详细的理论讨论。 长期以来，深度学习的动量一直被认为是有益的。 有关实例的详细信息，请参阅 (Sutskever et al., 2013)的讨论。

6.1.2. 条件不佳的问题

为了更好地了解动量法的几何属性，我们复习一下梯度下降，尽管它的目标函数明显不那么令人愉快。 回想我们在 11.3节中使用了 ，即中度扭曲的椭球目标。 我们通过向 方向伸展它来进一步扭曲这个函数

与之前一样， 在 (0, 0) 有最小值， 该函数在 的方向上非常平坦。 让我们看看在这个新函数上执行梯度下降时会发生什么。

python 复制代码 
# %matplotlib inline
import torch
eta = 0.4
def f_2d(x1, x2):
    return 0.1 * x1 ** 2 + 2 * x2 ** 2
def gd_2d(x1, x2, s1, s2):
    return (x1 - eta * 0.2 * x1, x2 - eta * 4 * x2, 0, 0)

d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

从构造来看，x2 方向的梯度比水平 x1 方向的梯度大得多，变化也快得多。 因此，我们陷入两难：如果选择较小的学习率，我们会确保解不会在 x2 方向发散，但要承受在 x1 方向的缓慢收敛。相反，如果学习率较高，我们在 x1 方向上进展很快，但在 x2 方向将会发散。 下面的例子说明了即使学习率从 0.4 略微提高到 0.6 ，也会发生变化。 x1 方向上的收敛有所改善，但整体来看解的质量更差了。

python 复制代码 
eta = 0.6
d2l.show_trace_2d(f_2d, d2l.train_2d(gd_2d))

6.1.3. 动量法

动量法 （momentum）使我们能够解决上面描述的梯度下降问题。 观察上面的优化轨迹，我们可能会直觉到计算过去的平均梯度效果会很好。 毕竟，在 x1 方向上，这将聚合非常对齐的梯度，从而增加我们在每一步中覆盖的距离。 相反，在梯度振荡的 x2 方向，由于相互抵消了对方的振荡，聚合梯度将减小步长大小。 使用 而不是梯度 可以生成以下更新等式：

请注意，对于 ，我们恢复常规的梯度下降。 在深入研究它的数学属性之前，让我们快速看一下算法在实验中的表现如何。

python 复制代码 
def momentum_2d(x1, x2, v1, v2):
    v1 = beta * v1 + 0.2 * x1
    v2 = beta * v2 + 4 * x2
    return x1 - eta * v1, x2 - eta * v2, v1, v2

eta, beta = 0.6, 0.5
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

正如所见，尽管学习率与我们以前使用的相同，动量法仍然很好地收敛了。 让我们看看当降低动量参数时会发生什么。 将其减半至 会导致一条几乎没有收敛的轨迹。 尽管如此，它比没有动量时解将会发散要好得多。

python 复制代码 
eta, beta = 0.6, 0.25
d2l.show_trace_2d(f_2d, d2l.train_2d(momentum_2d))

请注意，我们可以将动量法与随机梯度下降，特别是小批量随机梯度下降结合起来。 唯一的变化是，在这种情况下，我们将梯度 替换为 。 为了方便起见，我们在时间 t = 0 初始化 。

6.1.4. 有效样本权重

回想一下 。 极限条件下， 。 换句话说，不同于在梯度下降或者随机梯度下降中取步长 ，我们选取步长 ，同时处理潜在表现可能会更好的下降方向。 这是集两种好处于一身的做法。 为了说明 的不同选择的权重效果如何，请参考下面的图表。

python 复制代码 
d2l.set_figsize()
betas = [0.95, 0.9, 0.6, 0]
for beta in betas:
    x = torch.arange(40).detach().numpy()
    d2l.plt.plot(x, beta ** x, label=f'beta = {beta:.2f}')
d2l.plt.xlabel('time')
d2l.plt.legend();

6.2. 实际实验

让我们来看看动量法在实验中是如何运作的。 为此，我们需要一个更加可扩展的实现。

6.2.1. 从零开始实现

相比于小批量随机梯度下降，动量方法需要维护一组辅助变量，即速度。 它与梯度以及优化问题的变量具有相同的形状。 在下面的实现中，我们称这些变量为states。

python 复制代码 
def init_momentum_states(feature_dim):
    v_w = torch.zeros((feature_dim, 1))
    v_b = torch.zeros(1)
    return (v_w, v_b)

def sgd_momentum(params, states, hyperparams):
    for p, v in zip(params, states):
        with torch.no_grad():
            v[:] = hyperparams['momentum'] * v + p.grad
            p[:] -= hyperparams['lr'] * v
        p.grad.data.zero_()

让我们看看它在实验中是如何运作的。

python 复制代码 
def train_momentum(lr, momentum, num_epochs=2):
    d2l.train_ch11(sgd_momentum, init_momentum_states(feature_dim),
                   {'lr': lr, 'momentum': momentum}, data_iter,
                   feature_dim, num_epochs)

data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
train_momentum(0.02, 0.5)

当我们将动量超参数momentum增加到0.9时，它相当于有效样本数量增加到 。 我们将学习率略微降至 0.01 ，以确保可控。

python 复制代码 
train_momentum(0.01, 0.9)

降低学习率进一步解决了任何非平滑优化问题的困难，将其设置为 0.005 会产生良好的收敛性能。

python 复制代码 
train_momentum(0.005, 0.9)

6.2.2. 简洁实现

由于深度学习框架中的优化求解器早已构建了动量法，设置匹配参数会产生非常类似的轨迹。

python 复制代码 
trainer = torch.optim.SGD
d2l.train_concise_ch11(trainer, {'lr': 0.005, 'momentum': 0.9}, data_iter)

6.3. 理论分析

的2D示例似乎相当牵强。 下面我们将看到，它在实际生活中非常具有代表性，至少最小化凸二次目标函数的情况下是如此。

6.3.1. 二次凸函数

考虑这个函数

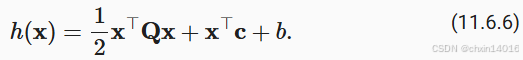
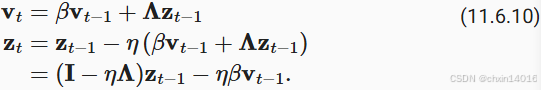
在这样做的过程中，我们只是证明了以下定理：带有和带有不凸二次函数动量的梯度下降，可以分解为朝二次矩阵特征向量方向坐标顺序的优化。

6.3.2. 标量函数

鉴于上述结果，让我们看看当我们最小化函数 时会发生什么。 对于梯度下降我们有

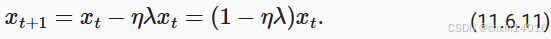
每 时，这种优化以指数速度收敛，因为在 t 步之后我们可以得到 。 这显示了在我们将学习率 提高到 之前，收敛率最初是如何提高的。 超过该数值之后，梯度开始发散，对于 而言，优化问题将会发散。

python 复制代码 
lambdas = [0.1, 1, 10, 19]
eta = 0.1
d2l.set_figsize((6, 4))
for lam in lambdas:
    t = torch.arange(20).detach().numpy()
    d2l.plt.plot(t, (1 - eta * lam) ** t, label=f'lambda = {lam:.2f}')
d2l.plt.xlabel('time')
d2l.plt.legend();

为了分析动量的收敛情况，我们首先用两个标量重写更新方程：一个用于 x ，另一个用于动量 v 。这产生了：

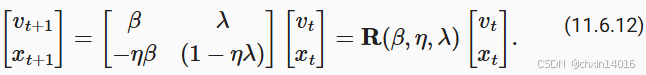
我们用 来表示 2×2 管理的收敛表现。 在 t 步之后，最初的值 变为 。 因此，收敛速度是由 的特征值决定的。 请参阅文章 (Goh, 2017)了解精彩动画。 请参阅 (Flammarion and Bach, 2015)了解详细分析。 简而言之，当 时动量收敛。 与梯度下降的 相比，这是更大范围的可行参数。 另外，一般而言较大值的是可取的。

小结

  • 动量法用过去梯度的平均值来替换梯度，这大大加快了收敛速度。

  • 对于无噪声梯度下降和嘈杂随机梯度下降，动量法都是可取的。

  • 动量法可以防止在随机梯度下降的优化过程停滞的问题。

  • 由于对过去的数据进行了指数降权，有效梯度数为 。

  • 在凸二次问题中，可以对动量法进行明确而详细的分析。

  • 动量法的实现非常简单，但它需要我们存储额外的状态向量（动量v）。

7. AdaGrad算法

Adagrad​​：根据历史梯度平方和为每个参数自适应调整学习率

7.1. 稀疏特征和学习率

7.2. 预处理

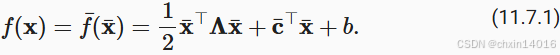
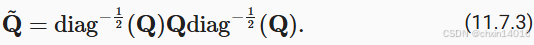
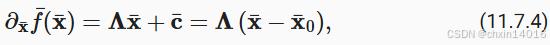
7.3. 算法

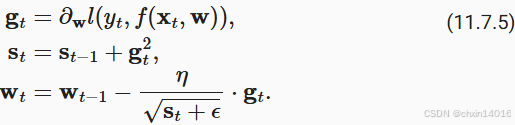
7.4. 从零开始实现

同动量法一样，AdaGrad算法需要对每个自变量维护同它一样形状的状态变量。

python 复制代码 
def init_adagrad_states(feature_dim):
    s_w = np.zeros((feature_dim, 1))
    s_b = np.zeros(1)
    return (s_w, s_b)

def adagrad(params, states, hyperparams):
    eps = 1e-6
    for p, s in zip(params, states):
        s[:] += np.square(p.grad)
        p[:] -= hyperparams['lr'] * p.grad / np.sqrt(s + eps)

7.5. 简洁实现

我们可直接使用深度学习框架中提供的AdaGrad算法来训练模型。

python 复制代码 
trainer = torch.optim.Adagrad
d2l.train_concise_ch11(trainer, {'lr': 0.1}, data_iter)

7.6. 小结

  • AdaGrad算法会在单个坐标层面动态降低学习率。

  • AdaGrad算法利用梯度的大小作为调整进度速率的手段：用较小的学习率来补偿带有较大梯度的坐标。

  • 在深度学习问题中，由于内存和计算限制，计算准确的二阶导数通常是不可行的。梯度可以作为一个有效的代理。

  • 如果优化问题的结构相当不均匀，AdaGrad算法可以帮助缓解扭曲。

  • AdaGrad算法对于稀疏特征特别有效，在此情况下由于不常出现的问题，学习率需要更慢地降低。

  • 在深度学习问题上，AdaGrad算法有时在降低学习率方面可能过于剧烈。我们将在 11.10节一节讨论缓解这种情况的策略。

8. RMSProp算法

（7. AdaGrad算法）中的关键问题之一，是学习率按预定时间

8.1. 算法

9. Adadelta（AdaGrad的另一种变体）

Adadelta是AdaGrad的另一种变体（7. AdaGrad算法）， 主要区别在于前者减少了学习率适应坐标的数量。 此外，广义上Adadelta被称为没有学习率，因为它使用变化量本身作为未来变化的校准。 Adadelta算法是在 (Zeiler, 2012)中提出的

9.1. Adadelta算法

9.2. 代码实现

python 复制代码 
%matplotlib inline
import torch
from d2l import torch as d2l


def init_adadelta_states(feature_dim):
    s_w, s_b = torch.zeros((feature_dim, 1)), torch.zeros(1)
    delta_w, delta_b = torch.zeros((feature_dim, 1)), torch.zeros(1)
    return ((s_w, delta_w), (s_b, delta_b))

def adadelta(params, states, hyperparams):
    rho, eps = hyperparams['rho'], 1e-5
    for p, (s, delta) in zip(params, states):
        with torch.no_grad():
            # In-placeupdatesvia[:]
            s[:] = rho * s + (1 - rho) * torch.square(p.grad)
            g = (torch.sqrt(delta + eps) / torch.sqrt(s + eps)) * p.grad
            p[:] -= g
            delta[:] = rho * delta + (1 - rho) * g * g
        p.grad.data.zero_()

小结

  • Adadelta没有学习率参数。相反，它使用参数本身的变化率来调整学习率。

  • Adadelta需要两个状态变量来存储梯度的二阶导数和参数的变化。

  • Adadelta使用泄漏的平均值来保持对适当统计数据的运行估计。

10. Adam算法

Adam优化器​​：为每个参数维护不同的学习率（一阶矩和二阶矩）

本章我们已经学习了许多有效优化的技术。 在本节讨论之前，我们先详细回顾一下这些技术：

  • （4. 随机梯度下降）中，我们学习了：随机梯度下降在解决优化问题时比梯度下降更有效。
  • （5. 小批量随机梯度下降）中，我们学习了：在一个小批量中使用更大的观测值集，可以通过向量化提供额外效率。这是高效的多机、多GPU和整体并行处理的关键。
  • （6. 动量法）：添加了一种机制，用于汇总过去梯度的历史以加速收敛。
  • （7. AdaGrad算法 ）：我们通过对每个坐标缩放来实现高效计算的预处理器。
  • （8. RMSProp算法）：我们通过学习率的调整来分离每个坐标的缩放。

Adam算法 (Kingma and Ba, 2014)将所有这些技术汇总到一个高效的学习算法中。 不出预料，作为深度学习中使用的更强大和有效的优化算法之一，它非常受欢迎。 但是它并非没有问题，尤其是 (Reddi et al., 2019)表明，有时Adam算法可能由于方差控制不良而发散。 在完善工作中， (Zaheer et al., 2018)给Adam算法提供了一个称为Yogi的热补丁来解决这些问题。 下面我们了解一下Adam算法。

10.1. 算法

Adam算法的关键组成部分之一是：它使用指数加权移动平均值来估算梯度的动量和二次矩，即它使用状态变量

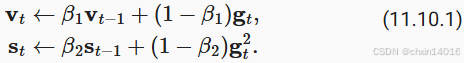
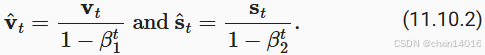
10.2. 实现

从头开始实现Adam算法并不难。 为方便起见，我们将时间步存储在hyperparams字典中。 除此之外，一切都很简单。

python 复制代码 
%matplotlib inline
import torch
from d2l import torch as d2l


def init_adam_states(feature_dim):
    v_w, v_b = torch.zeros((feature_dim, 1)), torch.zeros(1)
    s_w, s_b = torch.zeros((feature_dim, 1)), torch.zeros(1)
    return ((v_w, s_w), (v_b, s_b))

def adam(params, states, hyperparams):
    beta1, beta2, eps = 0.9, 0.999, 1e-6
    for p, (v, s) in zip(params, states):
        with torch.no_grad():
            v[:] = beta1 * v + (1 - beta1) * p.grad
            s[:] = beta2 * s + (1 - beta2) * torch.square(p.grad)
            v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
            s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
            p[:] -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr)
                                                       + eps)
        p.grad.data.zero_()
    hyperparams['t'] += 1

现在，我们用以上Adam算法来训练模型，这里我们使用 的学习率。

python 复制代码 
data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
d2l.train_ch11(adam, init_adam_states(feature_dim),
               {'lr': 0.01, 't': 1}, data_iter, feature_dim);

此外，我们可以用深度学习框架自带算法应用Adam算法，这里我们只需要传递配置参数。

python 复制代码 
trainer = torch.optim.Adam
d2l.train_concise_ch11(trainer, {'lr': 0.01}, data_iter)

10.3. Yogi

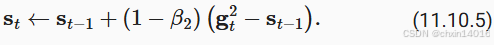
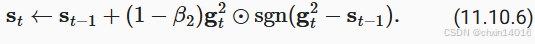
论文中，作者还进一步建议用更大的初始批量来初始化动量，而不仅仅是初始的逐点估计。

python 复制代码 
def yogi(params, states, hyperparams):
    beta1, beta2, eps = 0.9, 0.999, 1e-3
    for p, (v, s) in zip(params, states):
        with torch.no_grad():
            v[:] = beta1 * v + (1 - beta1) * p.grad
            s[:] = s + (1 - beta2) * torch.sign(
                torch.square(p.grad) - s) * torch.square(p.grad)
            v_bias_corr = v / (1 - beta1 ** hyperparams['t'])
            s_bias_corr = s / (1 - beta2 ** hyperparams['t'])
            p[:] -= hyperparams['lr'] * v_bias_corr / (torch.sqrt(s_bias_corr)
                                                       + eps)
        p.grad.data.zero_()
    hyperparams['t'] += 1

data_iter, feature_dim = d2l.get_data_ch11(batch_size=10)
d2l.train_ch11(yogi, init_adam_states(feature_dim),
               {'lr': 0.01, 't': 1}, data_iter, feature_dim);

小结

  • Adam算法将许多优化算法的功能结合到了相当强大的更新规则中。

  • Adam算法在RMSProp算法基础上创建的，还在小批量的随机梯度上使用EWMA。

  • 在估计动量和二次矩时，Adam算法使用偏差校正来调整缓慢的启动速度。

  • 对于具有显著差异的梯度，我们可能会遇到收敛性问题。我们可以通过使用更大的小批量或者切换到改进的估计值来修正它们。Yogi提供了这样的替代方案。

11. 学习率调度器

到目前为止，我们主要关注如何更新权重向量的优化算法，而不是它们的更新速率。 然而，调整学习率通常与实际算法同样重要，有如下几方面需要考虑：

  • 首先，学习率的大小很重要。如果它太大，优化就会发散；如果它太小，训练就会需要过长时间，或者我们最终只能得到次优的结果。我们之前看到问题的条件数很重要（有关详细信息，请参见 11.6节）。直观地说，这是最不敏感与最敏感方向的变化量的比率。
  • 其次，衰减速率同样很重要。如果学习率持续过高，我们可能最终会在最小值附近弹跳，从而无法达到最优解。 11.5节比较详细地讨论了这一点，在 11.4节中我们则分析了性能保证。简而言之，我们希望速率衰减，但要比 慢，这样能成为解决凸问题的不错选择。
  • 另一个同样重要的方面是初始化。这既涉及参数最初的设置方式（详情请参阅 4.8节），又关系到它们最初的演变方式。这被戏称为预热（warmup），即我们最初开始向着解决方案迈进的速度有多快。一开始的大步可能没有好处，特别是因为最初的参数集是随机的。最初的更新方向可能也是毫无意义的。
  • 最后，还有许多优化变体可以执行周期性学习率调整。这超出了本章的范围，我们建议读者阅读 (Izmailov et al., 2018)来了解个中细节。例如，如何通过对整个路径参数求平均值来获得更好的解。

鉴于管理学习率需要很多细节，因此大多数深度学习框架都有自动应对这个问题的工具。 在本章中，我们将梳理不同的调度策略对准确性的影响，并展示如何通过学习率调度器（learning rate scheduler）来有效管理。

11.1. 一个简单的问题

我们从一个简单的问题开始，这个问题可以轻松计算，但足以说明要义。 为此，我们选择了一个稍微现代化的LeNet版本（激活函数使用relu而不是sigmoid，汇聚层使用最大汇聚层而不是平均汇聚层），并应用于Fashion-MNIST数据集。 此外，我们混合网络以提高性能。 由于大多数代码都是标准的，我们只介绍基础知识，而不做进一步的详细讨论。如果需要，请参阅（现代卷积神经网络------动手学深度学习7_现代卷积神经网络学习-CSDN博客）进行复习。

python 复制代码 
%matplotlib inline
import math
import torch
from torch import nn
from torch.optim import lr_scheduler
from d2l import torch as d2l


def net_fn():
    model = nn.Sequential(
        nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.ReLU(),
        nn.MaxPool2d(kernel_size=2, stride=2),
        nn.Conv2d(6, 16, kernel_size=5), nn.ReLU(),
        nn.MaxPool2d(kernel_size=2, stride=2),
        nn.Flatten(),
        nn.Linear(16 * 5 * 5, 120), nn.ReLU(),
        nn.Linear(120, 84), nn.ReLU(),
        nn.Linear(84, 10))

    return model

loss = nn.CrossEntropyLoss()
device = d2l.try_gpu()

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=batch_size)

# 代码几乎与d2l.train_ch6定义在卷积神经网络一章LeNet一节中的相同
def train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
          scheduler=None):
    net.to(device)
    animator = d2l.Animator(xlabel='epoch', xlim=[0, num_epochs],
                            legend=['train loss', 'train acc', 'test acc'])

    for epoch in range(num_epochs):
        metric = d2l.Accumulator(3)  # train_loss,train_acc,num_examples
        for i, (X, y) in enumerate(train_iter):
            net.train()
            trainer.zero_grad()
            X, y = X.to(device), y.to(device)
            y_hat = net(X)
            l = loss(y_hat, y)
            l.backward()
            trainer.step()
            with torch.no_grad():
                metric.add(l * X.shape[0], d2l.accuracy(y_hat, y), X.shape[0])
            train_loss = metric[0] / metric[2]
            train_acc = metric[1] / metric[2]
            if (i + 1) % 50 == 0:
                animator.add(epoch + i / len(train_iter),
                             (train_loss, train_acc, None))

        test_acc = d2l.evaluate_accuracy_gpu(net, test_iter)
        animator.add(epoch+1, (None, None, test_acc))

        if scheduler:
            if scheduler.__module__ == lr_scheduler.__name__:
                # UsingPyTorchIn-Builtscheduler
                scheduler.step()
            else:
                # Usingcustomdefinedscheduler
                for param_group in trainer.param_groups:
                    param_group['lr'] = scheduler(epoch)

    print(f'train loss {train_loss:.3f}, train acc {train_acc:.3f}, '
          f'test acc {test_acc:.3f}')

让我们来看看如果使用默认设置，调用此算法会发生什么。 例如设学习率为0.03并训练30次迭代。 留意在超过了某点、测试准确度方面的进展停滞时，训练准确度将如何继续提高。 两条曲线之间的间隙表示过拟合。

python 复制代码 
lr, num_epochs = 0.3, 30
net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train(net, train_iter, test_iter, num_epochs, loss, trainer, device)

11.2. 学习率调度器

我们可以在每个迭代轮数（甚至在每个小批量）之后向下调整学习率。 例如，以动态的方式来响应优化的进展情况。

python 复制代码 
lr = 0.1
trainer.param_groups[0]["lr"] = lr
print(f'learning rate is now {trainer.param_groups[0]["lr"]:.2f}')

更通常而言，我们应该定义一个调度器。 当调用更新次数时，它将返回学习率的适当值。 让我们定义一个简单的方法，将学习率设置为 。

python 复制代码 
class SquareRootScheduler:
    def __init__(self, lr=0.1):
        self.lr = lr

    def __call__(self, num_update):
        return self.lr * pow(num_update + 1.0, -0.5)

让我们在一系列值上绘制它的行为。

python 复制代码 
scheduler = SquareRootScheduler(lr=0.1)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])

现在让我们来看看这对在Fashion-MNIST数据集上的训练有何影响。 我们只是提供调度器作为训练算法的额外参数。

python 复制代码 
net = net_fn()
trainer = torch.optim.SGD(net.parameters(), lr)
train(net, train_iter, test_iter, num_epochs, loss, trainer, device,
      scheduler)

这比以前好一些：曲线比以前更加平滑，并且过拟合更小了。 遗憾的是，关于为什么在理论上某些策略会导致较轻的过拟合，有一些观点认为，较小的步长将导致参数更接近零，因此更简单。 但是，这并不能完全解释这种现象，因为我们并没有真正地提前停止，而只是轻柔地降低了学习率。

11.3. 策略

虽然我们不可能涵盖所有类型的学习率调度器，但我们会尝试在下面简要概述常用的策略：多项式衰减和分段常数表。 此外，余弦学习率调度在实践中的一些问题上运行效果很好。 在某些问题上，最好在使用较高的学习率之前预热优化器。

11.3.1. 单因子调度器

11.3.2. 多因子调度器

11.3.3. 余弦调度器

11.3.4. 预热

小结

  • 在训练期间逐步降低学习率可以提高准确性，并且减少模型的过拟合。

  • 在实验中，每当进展趋于稳定时就降低学习率，这是很有效的。从本质上说，这可以确保我们有效地收敛到一个适当的解，也只有这样才能通过降低学习率来减小参数的固有方差。

  • 余弦调度器在某些计算机视觉问题中很受欢迎。

  • 优化之前的预热期可以防止发散。

  • 优化在深度学习中有多种用途。对于同样的训练误差而言，选择不同的优化算法和学习率调度，除了最大限度地减少训练时间，可以导致测试集上不同的泛化和过拟合量。

相关推荐
孤独野指针*P4 小时前
深度学习之美》读书笔记 - 第一章 & 第二章
人工智能·深度学习
闲人编程4 小时前
使用Python操作你的手机（Appium入门）
python·智能手机·appium·自动化·codecapsule·处理弹窗
大象耶4 小时前
Mamba与UNet融合的创新架构方向
论文阅读·人工智能·深度学习·计算机网络·机器学习
汤姆yu4 小时前
基于python大数据深度学习的酒店评论文本情感分析
开发语言·python·深度学习
遇雪长安4 小时前
深度学习YOLO实战：5、基于YOLO的自动化图像批量检测方案
人工智能·深度学习·yolo
浆果02074 小时前
【图像卷积基础】卷积过程&卷积实现通道扩充与压缩&池化Pooling原理和可视化
深度学习·神经网络·计算机视觉
拓端研究室4 小时前
Python电力负荷预测：LSTM、GRU、DeepAR、XGBoost、Stacking、ARIMA结合多源数据融合与SHAP可解释性的研究
python·gru·lstm
迷路爸爸1805 小时前
Git Commit Message 规范：写出清晰、可维护的提交记录
git·python
空空kkk5 小时前
Java——接口
java·开发语言·python
热门推荐
01BongoCat - 跨平台键盘猫动画工具02GitHub 镜像站点03UV安装并设置国内源04GitLab 零基础入门指南：从安装到项目管理全流程05Linux下V2Ray安装配置指南06Labelme从安装到标注：零基础完整指南072025软件测试面试八股文（含答案+文档）08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南09在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）10【vue篇】Vue 项目中的静态资源管理：assets vs static 终极指南