目录
引言:
今天是算法沉淀的第10天,前几天一直没有打算法题,所以今天除开昨天打的那场牛客基础赛的ABC,我们再打一道简单的dfs的算法题,来自洛谷,难度时普及/提高-
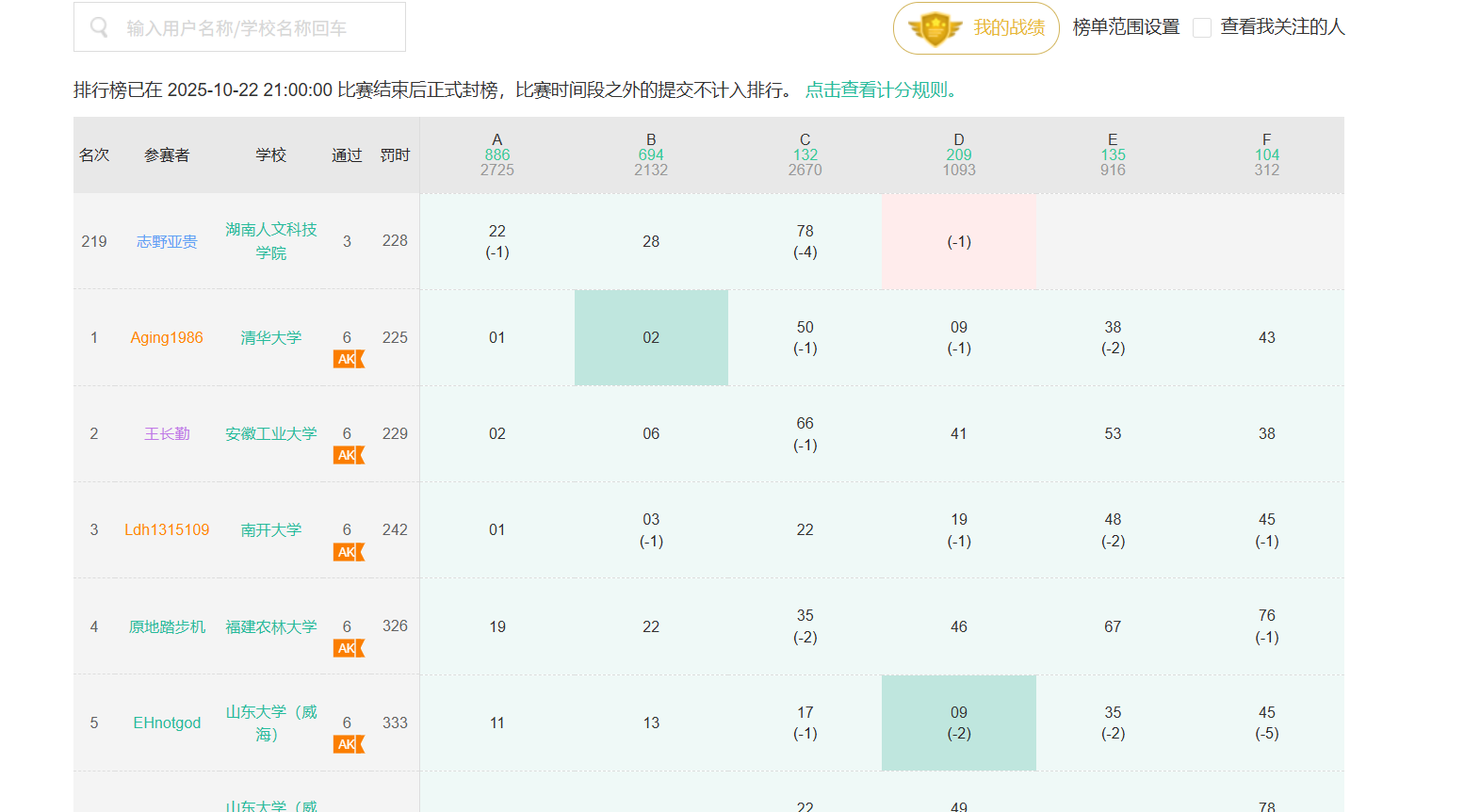
昨天的基础赛战绩如图
那么,话不多说,我们就进入今天的算法讲解--------------------->

牛客2025秋季算法编程训练联赛2-基础组
我们先来讲牛客比赛的题,因为这场我开出的题都挺简单的
做游戏
题目分析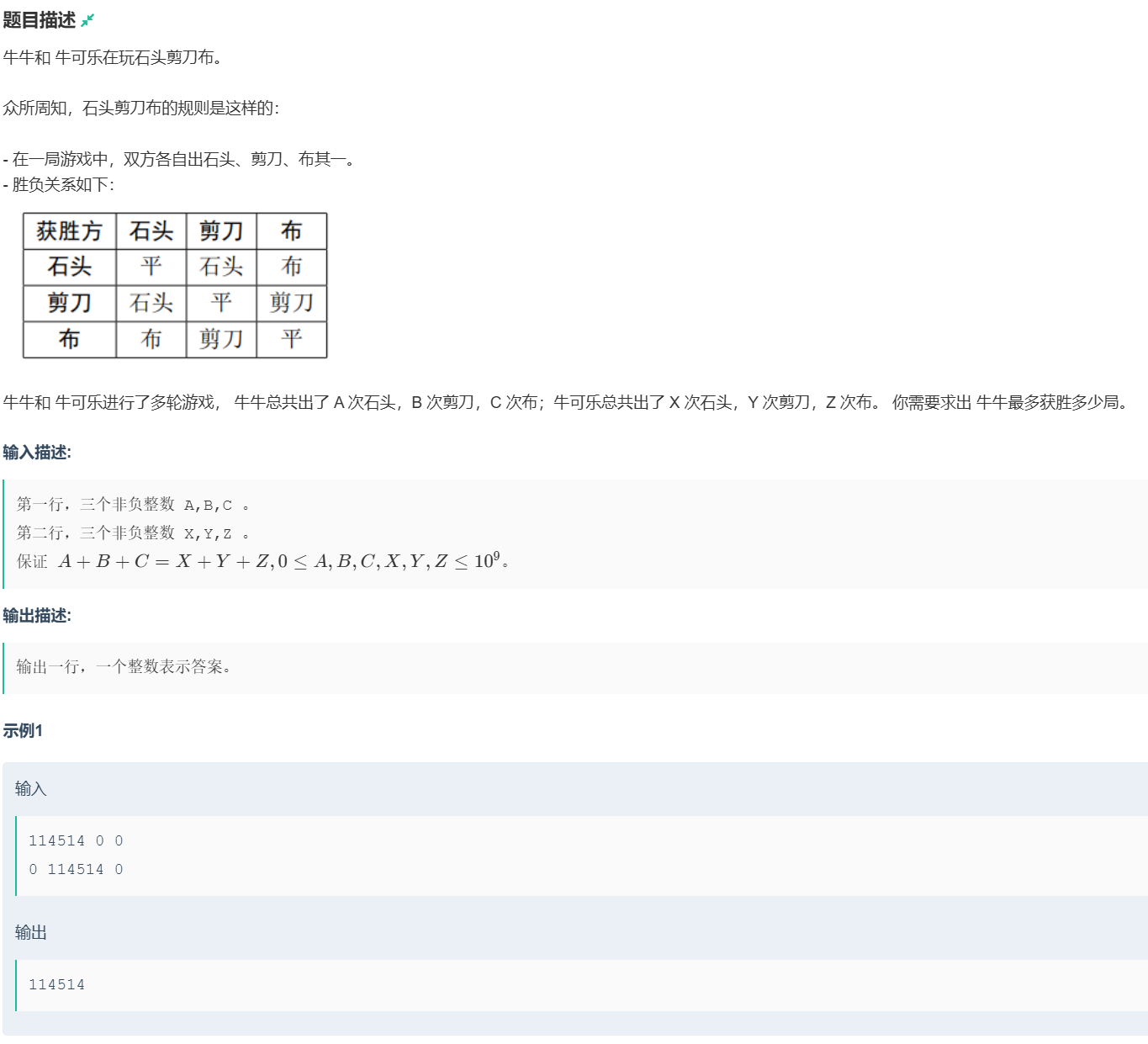
题目就是给你六个数,前三个数表示牛牛会出的石头次数,剪刀次数和布次数,后三个数表示牛可乐会出的石头次数,剪刀次数和布次数
然后题目问你牛牛最多能获胜多少场
逻辑梳理
这题只要让牛牛不管出什么都尽量赢就可以了
那么,我们假设牛牛的石头,剪刀,布数量分别是A,B,C
牛可乐的石头,剪刀,布数量分别是a,b,c
那么,如果牛牛出石头时候,牛可乐尽可能全出剪刀,这时候,牛牛出石头赢的场次的最大化便是min(A,b),同理,再把出剪刀和出布的情况分析一下,然后把三种情况的最大赢量都加起来就是答案了
代码实现
这里就直接放代码啦
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <map>
#include <vector>
using namespace std;
long long a, b, c, A, B, C;
void solve()
{
cin >> a >> b >> c >> A >> B >> C;
long long ans = 0;
ans = min(a, B) + min(b, C) + min(c, A);
cout << ans << endl;
}
int main()
{
solve();
return 0;
}排数字
题目分析
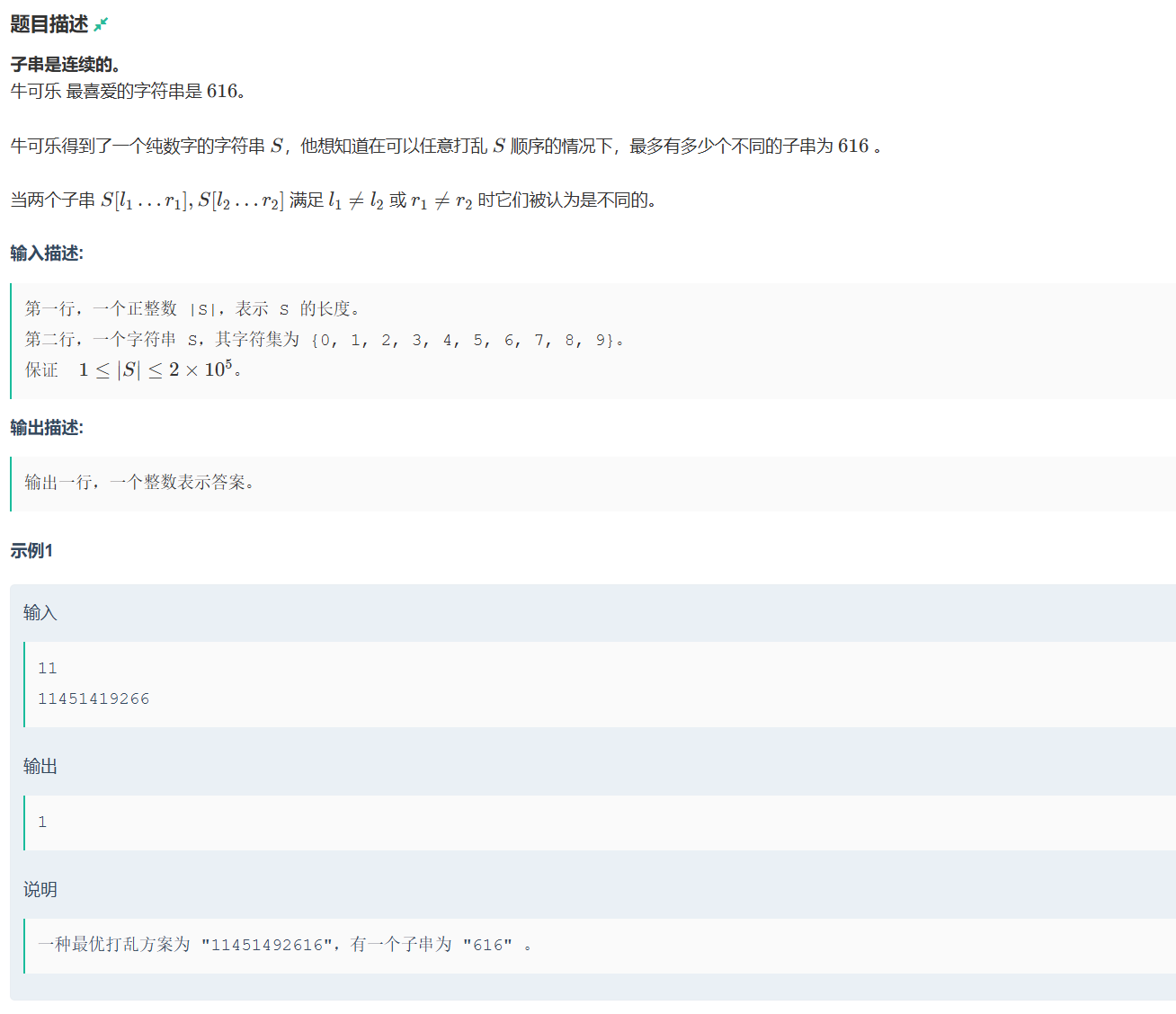
这题就是给你一个长度为n的一个字符串,然后这个字符串可以任意排序,问你616这样的子串最多有几个,然后输出个数就可以啦
逻辑梳理
这题我们来想一想什么情况下616的子串最多呢
是不是61616161616这样的情况子串是最多的
所以我们只需要统计6的个数和1的个数就可以了,然后组成上面那种排列情况,那么,如果要有n个满足条件的子序列,需要有n个1和n+1个6
所以我们只需要统计完个数后,取 1的个数 和 6的个数-1中的较小值,便是答案了
代码实现
这里就直接放代码啦
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <map>
#include <vector>
using namespace std;
void solve()
{
int yi = 0;
int liu = 0;
int n;
string s;
cin >> n;
cin >> s;
for (int i = 0; i < n; i++)
{
if (s[i] == '1')
yi++;
if (s[i] == '6')
liu++;
}
cout << min(yi, liu - 1) << endl;
}
int main()
{
solve();
return 0;
}判正误
题目分析
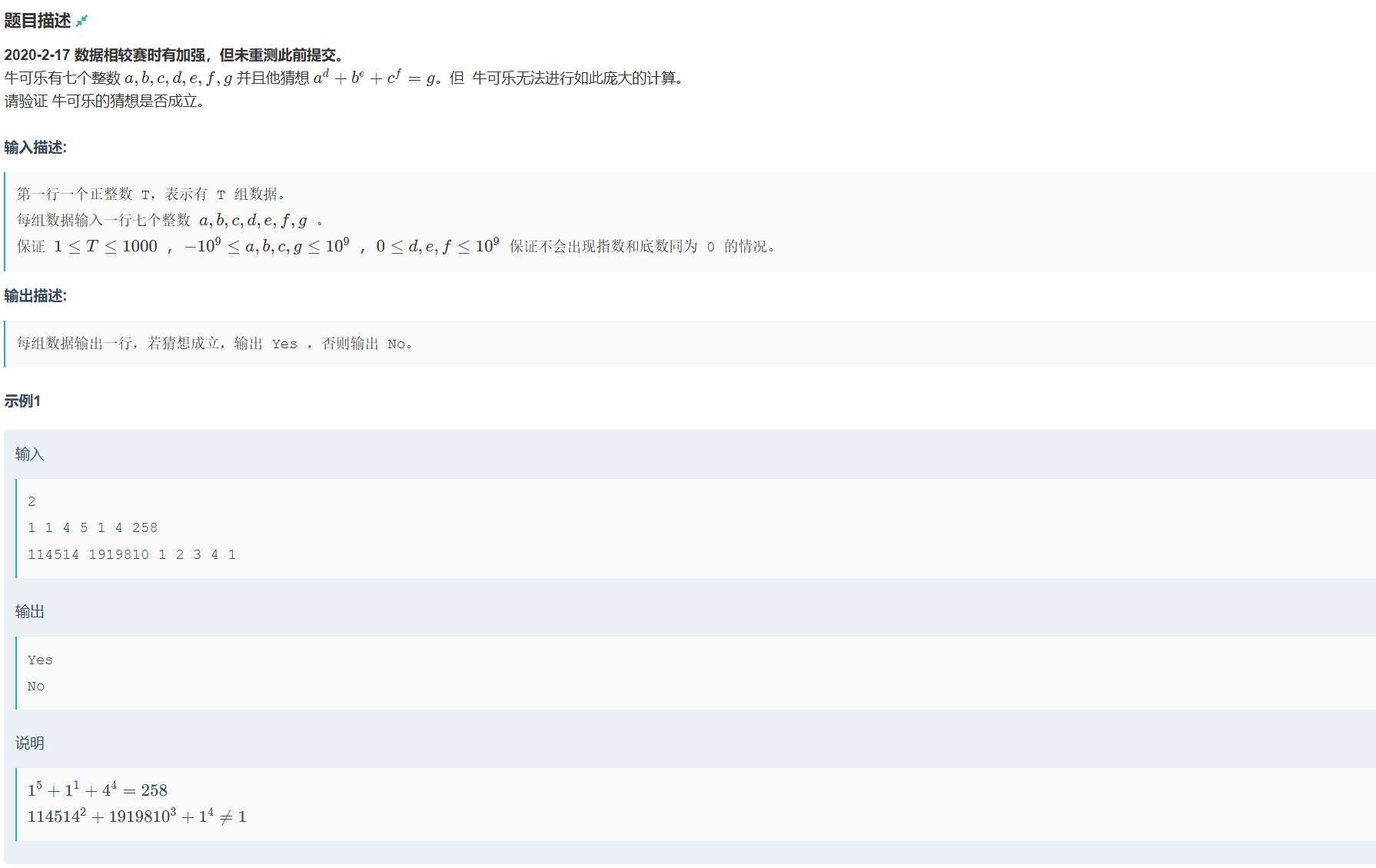
这题就是给你7个数a,b,c,d,e,f,g
然后问你a的d次+b的e次+c的f次=g这个式子成不成立
成立输出Yes,不成立输出No就可以啦
逻辑梳理
这题的数据范围给的很大,所以我们肯定不可能直接暴力算,那么,跟幂有关的算法我们想一想有什么呢,快速幂就很OK
我们快速幂的时候再模上一个比g大的值就可以啦
那么,g的范围是在1e9的,所以我们可以在快速幂的时候模个1e9+1或者1e10就可以了,当然数据类型不要忘了开long long
为什么用快速幂呢,因为直接算成不成立与取模后看成不成立是一样的,范围不超的话就不会用到取模,那就是单纯比较,如果超了范围,取模完的结果加起来跟g相比肯定是会出问题的,自然就不成立,当然,以防万一,你们也可以取模多组数,看结果影不影响
那么这题思路就讲解完啦,接下来进入代码实现环节
代码实现
这里就直接放代码啦
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <map>
#include <vector>
using namespace std;
int t;
long long mi(long long a, long long b, long long mo)
{
long long ans = 1;
while (b)
{
if (b & 1)
ans = (ans * a) % mo;
b >>= 1;
a = (a * a) % mo;
}
return ans;
}
void solve()
{
long long a, b, c, d, e, f, g;
cin >> a >> b >> c >> d >> e >> f >> g;
long long ans = mi(a, d, 1000000001) + mi(b, e, 1000000001) + mi(c,f, 1000000001);
if (ans == g)
cout << "Yes" << endl;
else
cout << "No" << endl;
}
int main()
{
cin >> t;
while (t--)
solve();
return 0;
}那么,这场牛客的题就讲到这啦
接下来,我们来讲一道dfs题
奇怪的电梯
题目分析
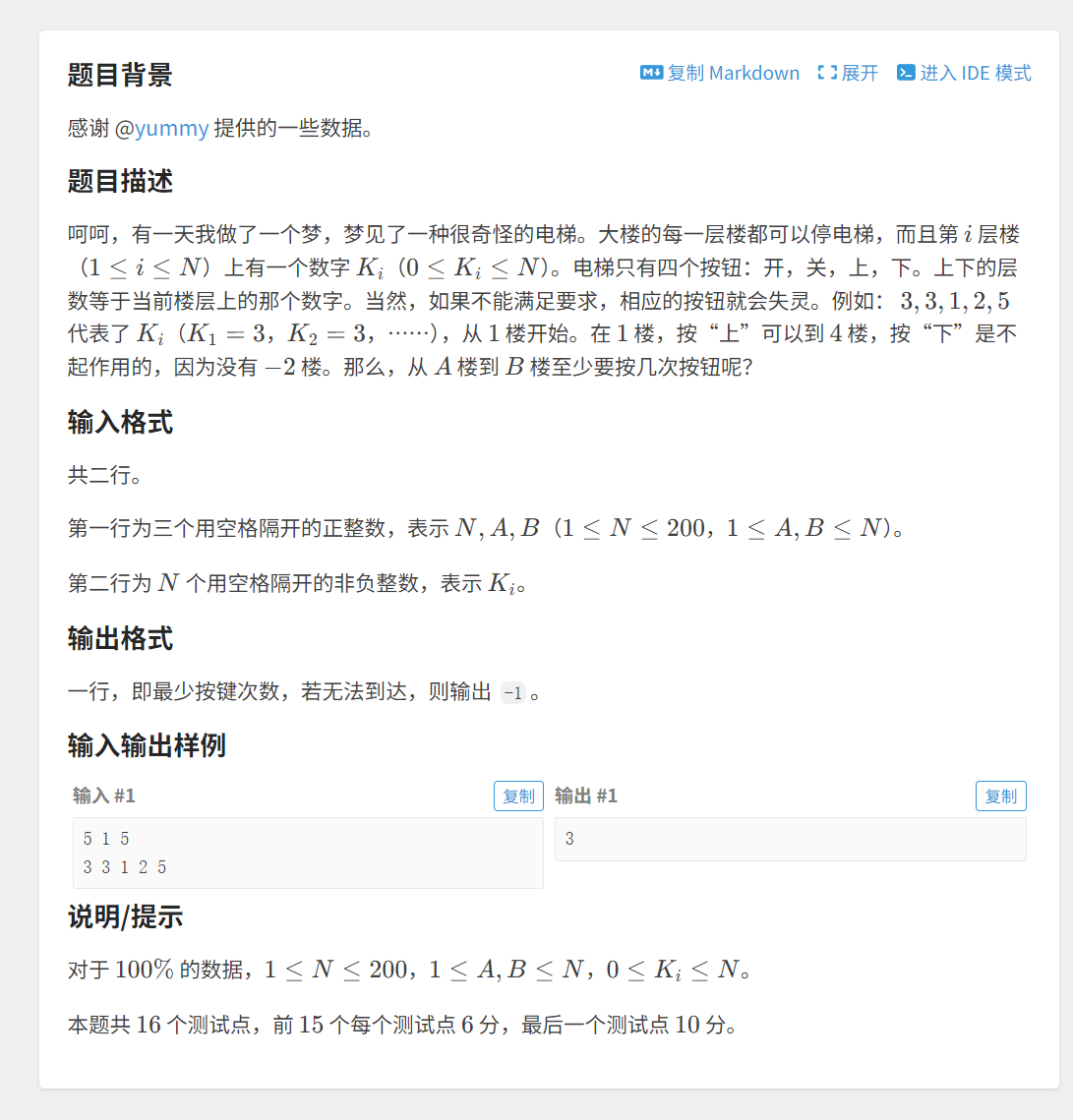
这题就是先告诉你有几个楼层,然后告诉你每一层楼时候电梯可以怎么动,向上ai层或者向下ai层,前提是不要超出楼的高度,也不要到低于一楼的地方去
然后有个人想要从a层到b层,问你最少要按几次按钮可以到
如果到的了就输出最少按钮次数
如果到不了,就输出-1就可以了
那么题目分析完了,我们进入逻辑梳理环节
逻辑梳理
这题看下面的数据就可以知道这是一道明显的dfs题,
我们可以选择让他往上,也可以选择让他往下,只有俩种情况,我们只需要把所有情况都用递归演示出来就可以了
然后到每层的最小步数我们就用一个数组来存,一开始先初始化成超大的一个值,如果最后递归结束了,我们需要到的位置的下标所对应的元素没有改变,就输出-1就可以了
这题dfs的影子已经很明显了,那么,思路梳理完,我们就进入代码实现的环节
代码实现
这里就直接放代码啦(下面的代码有一点需要注意,memset是按字节初始化的,所以判断时候因为是int类型,所以要3个3f)
cpp
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <map>
#include <vector>
using namespace std;
int n = 0;
int yi[210];
int vis[210];
void dfs(int a, int temp)
{
vis[a] = temp;
if (a + yi[a] <= n && temp + 1 < vis[a + yi[a]])
dfs(a + yi[a], temp + 1);
if (a - yi[a] > 0 && temp + 1 < vis[a - yi[a]])
dfs(a - yi[a], temp + 1);
}
void solve()
{
int a, b;
cin >> n >> a >> b;
for (int i = 1; i <= n; i++)
{
cin >> yi[i];
}
memset(vis, 0x3f3f3f, sizeof(vis));
dfs(a, 0);
if (vis[b] == 0x3f3f3f3f)
vis[b] = -1;
cout << vis[b] << endl;
return;
}
int main()
{
solve();
return 0;
}结语:
今日算法讲解到此结束啦,希望对你们有所帮助,谢谢观看,如果觉得不错可以分享给朋友哟。有什么看不懂的可以评论问哦,
