目录
[二、图的存储结构------非线性结构(m : n)](#二、图的存储结构——非线性结构(m : n))
图
一、图的基本概念
1、若 n 个顶点的无向图有 条边,称为无向完全图。
2、若 n 个顶点的有向图有 n(n-1) 条边,称为有向完全图。
3、稀疏图:边较少的图,边数 << 。
4、稠密图:边很多的图。无向图中边数接近 ;有向图中边数接近 n(n-1)。
5、带权树:边上带权的图 <=> 网络 。
6、弧头和弧尾:有向边 (u,v) 称为弧,边的始点 u 叫弧尾,终点 v 叫弧头。在有向图中顶点 v 的度等于该顶点的入度与出度之和。
7、问:当有向图中仅1个顶点的入度为0,其余顶点的入度均为1,此时是何形状?
答:是树,而且是一棵有向树。
8、生成树:是一个极小连通子图,它必含有图中全部顶点,但只有 n-1 条边。
(1)如果在生成树上添加1条边,必定构成一个环。
(2)若图中有 n 个顶点,却少于 n-1 条边,必为非连通图。
9、生成森林:由若干棵有向树组成,含全部顶点,但只有足以构成若干棵不相交的有向树的弧。
路劲长度:
(1)非带权图的路径长度是指此路径上边的条数
(2)带权图的路径长度是指此路径上各边的权之和
简单路径:路径上各顶点 、
、......、
均不相互重复
二、图的存储结构------非线性结构(m : n)
顺序存储结构
① 可用数组描述元素间的关系(多个顶点,无序可言)
② 图的顺序存储结构是指用数组(顺序表) 来存储图的顶点信息及顶点间的关系(边或弧),其核心是通过数组的下标或元素值描述顶点之间的邻接关系。与树的顺序存储不同,图的顶点之间没有固定的层次或父子关系("无序可言"),因此需要专门的结构记录顶点间的连接状态。
1、邻接矩阵表示法
(1) 建立一个顶点表(记录各个顶点信息)和一个邻接矩阵(表示各个顶点之间关系)
(2) 邻接矩阵(Adjacency Matrix)是图的一种基本顺序存储方式,通过一个二维数组表示顶点间的邻接关系,适用于无向图或有向图(无权图)。
(3) 有关系填1,没关系填0
(4)核心定义
- 设图有 n 个顶点,定义一个 n×n 的二维数组 A(称为邻接矩阵),其中:
- A[i][j]=1:表示顶点 i 与顶点 j 之间存在一条边(无向图)或弧(有向图,从 i 到 j)。
- A[i][j]=0:表示顶点 i 与顶点 j 之间不存在边或弧。
- 对于无向图,邻接矩阵是对称矩阵(A[i][j]=A[j][i]);对于有向图,邻接矩阵不一定对称。
示例1:
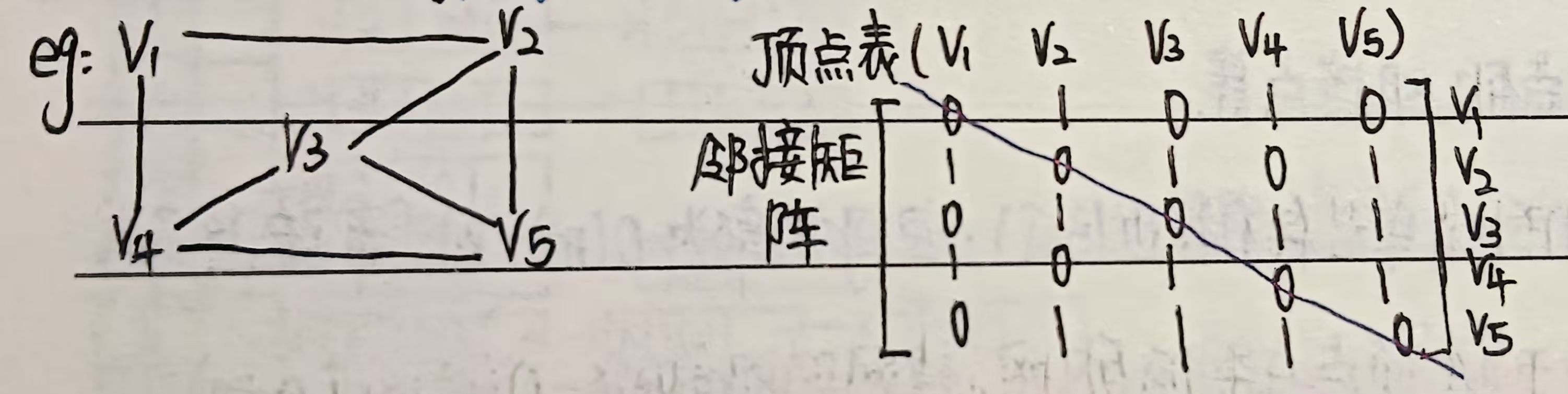
a. 无向图的邻接矩阵是对称的
b. 顶点 i 的度=第 i 行(列)中1的个数
c. 特点:完全图的邻接矩阵中,对角元素为0,其余全为1
示例2:
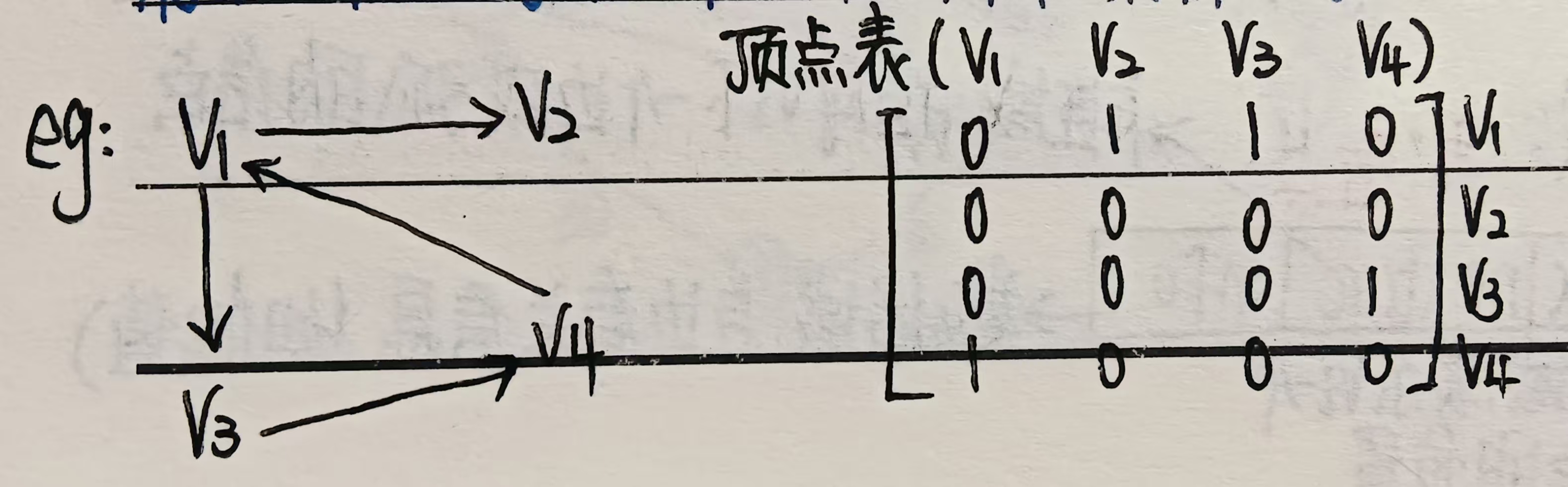
a. 在有向图的邻接矩阵中,第 i 行含义:以结点 为尾的弧(即出度边)
b. 在有向图的邻接矩阵中,第 i 列含义:以结点 为头的弧(即入度边)
c. 有向图的邻接矩阵可能是不对称的
d. 顶点的出度=第 i 行元素之和,
e. 顶点的入度=第 i 列元素之和,
f. 顶点的度=第 i 行元素之和+第 i 列元素之和,
示例3:
-
无向图:顶点集合 V={0,1,2,3},边集合 E={(0,1),(0,2),(1,2),(1,3)},邻接矩阵为:
0 1 2 3 0 0 1 1 0 1 1 0 1 1 2 1 1 0 0 3 0 1 0 0(对称矩阵,如 A[0][1]=A[1][0]=1,表示 0 和 1 之间有边)。
-
有向图:顶点集合 V={0,1,2},弧集合 E={<0,1>,<1,0>,<1,2>},邻接矩阵为:
0 1 2 0 0 1 0 1 1 0 1 2 0 0 0(非对称,如 A[0][1]=1 但 A[1][0]=1 是因为存在双向弧,而 A[1][2]=1 但 A[2][1]=0)。
(5)特点
- 优点:
- 判断两个顶点是否相邻(存在边)的时间复杂度为 O(1)(直接查 A[i][j])。
- 便于计算顶点的度(无向图中顶点 i 的度是第 i 行或第 i 列的和;有向图中出度是第 i 行的和,入度是第 i 列的和)。
- 容易实现图的操作,如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等。
- 缺点:
- n 个顶点需要 n*n 个单元存储边(弧)。
- 空间复杂度为 O(n2),不适合存储稀疏图(边数远小于 n2 的图),会浪费大量空间。
- 对于 n 个顶点 e 条弧的网,建网时间效率=
。
2、网(即有权图)的邻接矩阵
网(Network)是带权值的图(边或弧具有权重,如距离、成本等),其邻接矩阵是无权图邻接矩阵的扩展,通过二维数组存储顶点间的权重值。
① A.Edge[i][j]= (
)或<
>
② A.Edge[i][j]= ∞ 无边(弧)
③ 核心定义
- 设网有 n 个顶点,定义 n×n 的二维数组 A,其中:
- A[i][j]=w:表示顶点 i 与顶点 j 之间存在一条边或弧,权重为 w(w 为非负实数)。
- A[i][j]=∞(无穷大,通常用一个远超最大权重的数表示):表示顶点 i 与顶点 j 之间不存在边或弧。
- 对于无向网,邻接矩阵仍为对称矩阵(A[i][j]=A[j][i]);对于有向网,矩阵不一定对称。
- 顶点自身到自身的权重通常为 0(A[i][i]=0)。
示例1:
-
无向网:顶点集合 V={0,1,2},边及权重为 (0,1,5)、(0,2,3)、(1,2,1),邻接矩阵为:
0 1 2 0 0 5 3 1 5 0 1 2 3 1 0(对称,如 A[0][1]=A[1][0]=5,表示 0 和 1 之间的边权重为 5)。
-
有向网:顶点集合 V={0,1,2},弧及权重为 <0,1,2>、<1,2,3>、<2,0,4>,邻接矩阵为:
0 1 2 0 0 2 ∞ 1 ∞ 0 3 2 4 ∞ 0(非对称,如 A[0][1]=2 表示从 0 到 1 的弧权重为 2,而 A[1][0]=∞ 表示无反向弧)。
示例2:
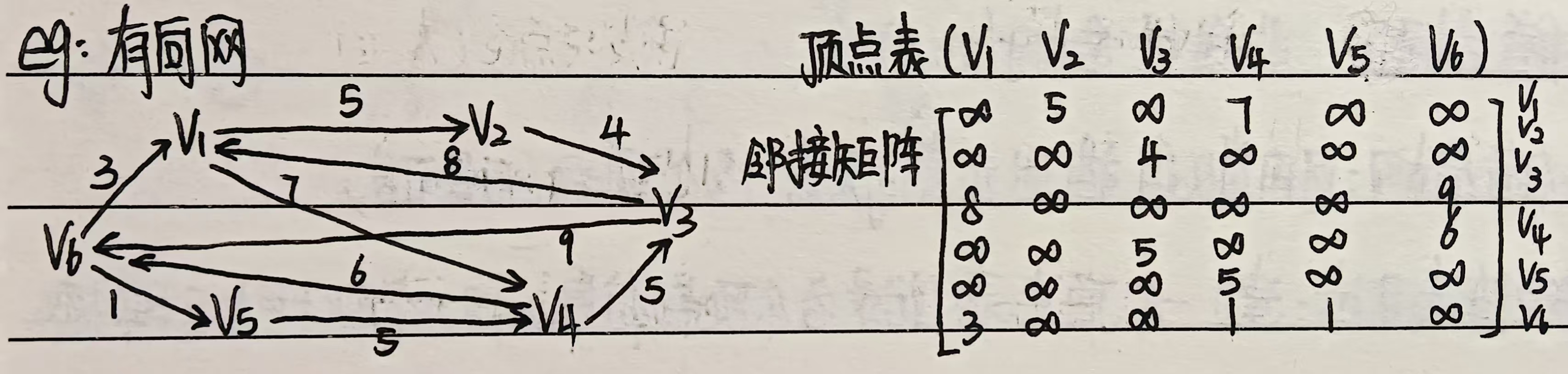
④ 特点
- 优点:
- 不仅能表示顶点间的邻接关系,还能直接存储权重,适合 Dijkstra、Floyd 等最短路径算法的实现(依赖权重快速访问)。
- 与无权图邻接矩阵一样,判断邻接和计算度(带权和)的效率高(O(1) 或 O(n))。
- 缺点:
- 空间复杂度仍为 O(n2),稀疏网(权值非 ∞ 的元素少)会浪费大量空间。
3、比较
| 类型 | 核心存储内容 | 空间复杂度 | 适用场景 |
|---|---|---|---|
| 邻接矩阵(无权图) | 0/1 表示是否有边 / 弧 | O(n2) | 稠密图、需频繁判断邻接关系 |
| 网的邻接矩阵 | 权重值 /∞ 表示边的权重 | O(n2) | 稠密网、需频繁访问权重(如最短路径计算) |
两者均通过二维数组实现,本质是用 "空间换时间",适合顶点数量固定且边数较多的图(稠密图 / 网);对于稀疏图 / 网,通常更适合用链式存储(如邻接表)。