用Python可视化深入理解极限存在的判定方法
在微积分的学习中,极限理论是整个数学分析的基础。而在这其中,夹逼定理 和单调有界收敛定理是判断极限是否存在的两个重要工具。本文将深入探讨这两个定理的数学原理,并通过Python代码演示如何应用这些定理解决实际问题。
一、夹逼定理:三方夹逼,确定极限
1. 定理阐述
夹逼定理是数学分析中的重要工具,它通过构建不等式关系来确定函数的极限值。定理的完整表述如下:
设函数 f(x)f(x)f(x),g(x)g(x)g(x),h(x)h(x)h(x) 在 x0x_0x0 的某去心邻域内有定义,且满足:
- 夹条件 :f(x)≤g(x)≤h(x)f(x) \leq g(x) \leq h(x)f(x)≤g(x)≤h(x)
- 逼条件 :limx→x0f(x)=limx→x0h(x)=A\lim \limits_{x \to x_0}f(x) = \lim \limits_{x \to x_0}h(x) = Ax→x0limf(x)=x→x0limh(x)=A
则 limx→x0g(x)=A\lim \limits_{x \to x_0}g(x) = Ax→x0limg(x)=A
2. 直观理解
可以将夹逼定理形象地理解为:如果函数 g(x)g(x)g(x) 始终被 f(x)f(x)f(x) 和 h(x)h(x)h(x) "夹在中间",而当 xxx 趋近于 x0x_0x0 时,f(x)f(x)f(x) 和 h(x)h(x)h(x) 都趋近于同一个值 AAA,那么 g(x)g(x)g(x) 也不得不趋近于 AAA。
3. Python代码验证
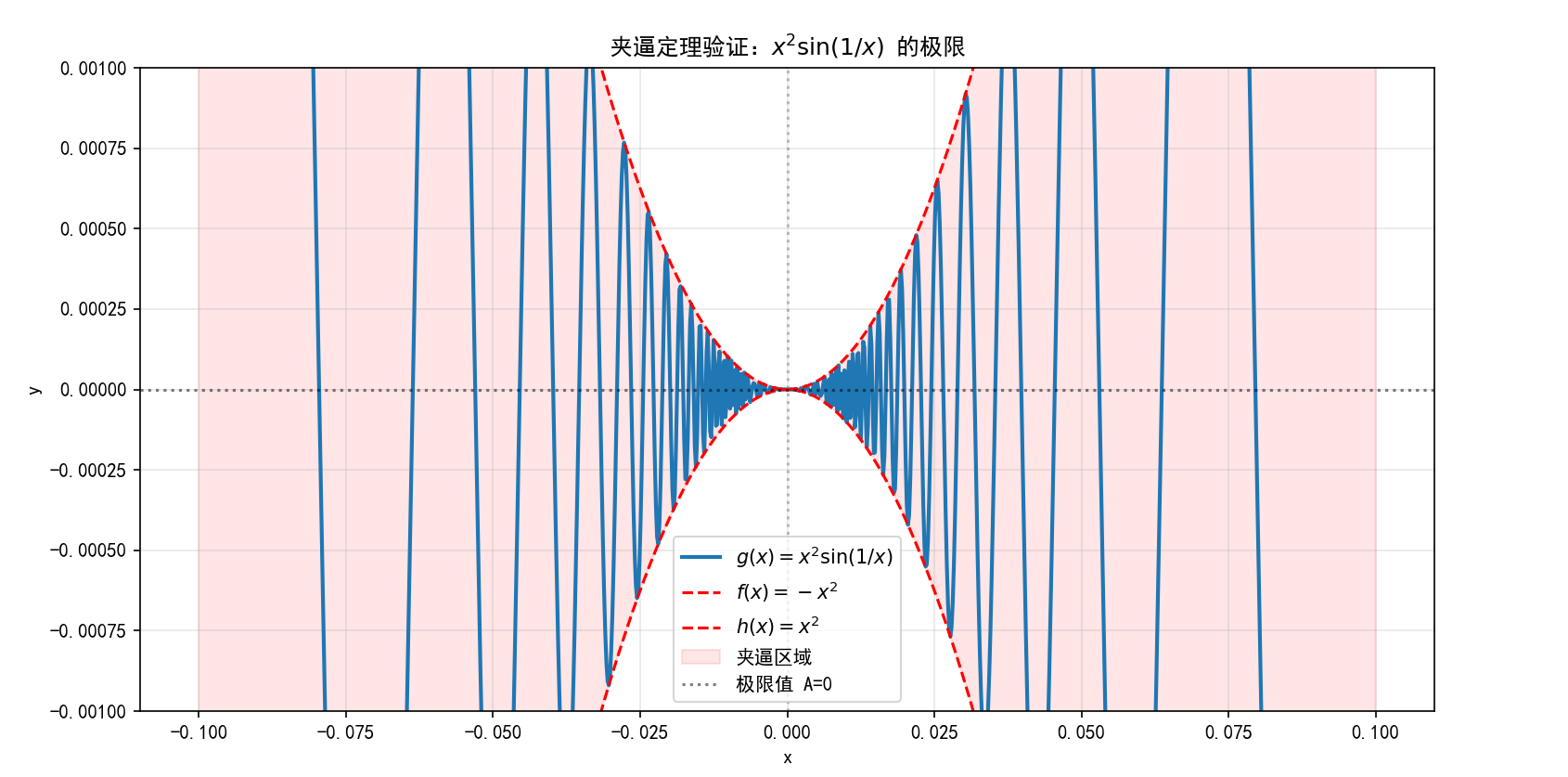
下面我们通过Python代码来验证夹逼定理的应用。考虑一个经典例子:证明 limx→0x2sin(1x)=0\lim \limits_{x \to 0} x^2 \sin(\frac{1}{x}) = 0x→0limx2sin(x1)=0。
我们知道,−1≤sin(1x)≤1-1 \leq \sin(\frac{1}{x}) \leq 1−1≤sin(x1)≤1,因此有 −x2≤x2sin(1x)≤x2-x^2 \leq x^2 \sin(\frac{1}{x}) \leq x^2−x2≤x2sin(x1)≤x2。当 x→0x \to 0x→0 时,−x2→0-x^2 \to 0−x2→0 且 x2→0x^2 \to 0x2→0,根据夹逼定理可得目标极限为0。
python
import numpy as np
import matplotlib.pyplot as plt
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 创建x值,排除x=0点
x = np.linspace(-0.1, 0.1, 1000)
x = x[x != 0] # 排除零点
# 计算函数值
f_x = x**2 * np.sin(1/x) # 目标函数
lower_bound = -x**2 # 下界函数
upper_bound = x**2 # 上界函数
# 绘制图像
plt.figure(figsize=(12, 6))
plt.plot(x, f_x, label=r'$g(x) = x^2 \sin(1/x)$', linewidth=2)
plt.plot(x, lower_bound, 'r--', label=r'$f(x) = -x^2$')
plt.plot(x, upper_bound, 'r--', label=r'$h(x) = x^2$')
plt.fill_between(x, lower_bound, upper_bound, color='red', alpha=0.1, label='夹逼区域')
plt.axhline(y=0, color='k', linestyle=':', alpha=0.5, label='极限值 A=0')
plt.axvline(x=0, color='gray', linestyle=':', alpha=0.5)
plt.xlabel('x')
plt.ylabel('y')
plt.title(r'夹逼定理验证:$x^2 \sin(1/x)$ 的极限')
plt.legend()
plt.grid(True, alpha=0.3)
plt.ylim(-0.001, 0.001)
plt.show()
# 计算x趋近于0时的函数值
print("x趋近于0时函数值的变化:")
x_values = [0.1, 0.01, 0.001, 0.0001]
for x_val in x_values:
g_val = x_val**2 * np.sin(1/x_val)
lower_val = -x_val**2
upper_val = x_val**2
print(f"x = {x_val:.4f}, g(x) = {g_val:.8f}, 下界 = {lower_val:.8f}, 上界 = {upper_val:.8f}")运行此代码,我们可以观察到当 xxx 趋近于 0 时,x2sin(1/x)x^2 \sin(1/x)x2sin(1/x) 的值确实被 −x2-x^2−x2 和 x2x^2x2 夹在中间,并且三者都趋近于 0。

4. 实际应用示例
夹逼定理特别适用于求解无法直接用极限运算法则求极限的函数极限,间接通过求得两个边界函数的极限来确定目标函数的极限。
例题 :求 limn→∞(1n2+1+1n2+2+⋯+1n2+n)\lim \limits_{n \to \infty} \left( \frac{1}{\sqrt{n^2+1}} + \frac{1}{\sqrt{n^2+2}} + \cdots + \frac{1}{\sqrt{n^2+n}} \right)n→∞lim(n2+1 1+n2+2 1+⋯+n2+n 1)
解 :对于每个 nnn,我们有: nn2+n≤1n2+1+1n2+2+⋯+1n2+n≤nn2+1\frac{n}{\sqrt{n^2+n}} \leq \frac{1}{\sqrt{n^2+1}} + \frac{1}{\sqrt{n^2+2}} + \cdots + \frac{1}{\sqrt{n^2+n}} \leq \frac{n}{\sqrt{n^2+1}}n2+n n≤n2+1 1+n2+2 1+⋯+n2+n 1≤n2+1 n
当 n→∞n \to \inftyn→∞ 时,左右两边的极限都是 1,因此由夹逼定理,原式的极限也是 1。
💡 互动挑战
尝试用Python代码验证上述例题的结果!你可以先计算几个较大的n值(如n=100, 1000, 10000)时的和,观察是否趋近于1。
二、单调有界收敛定理:单调有界必收敛
1. 定理阐述
单调有界收敛定理是判断数列极限存在性的重要工具:
- 如果数列 {an}\{a_n\}{an} 满足 an≤an+1a_n \leq a_{n+1}an≤an+1 (n=1,2,...n=1,2,...n=1,2,...) 且有上界,那么极限 limn→∞an\lim \limits_{n \to \infty}a_nn→∞liman 存在。
- 如果数列 {an}\{a_n\}{an} 满足 an≥an+1a_n \geq a_{n+1}an≥an+1 (n=1,2,...n=1,2,...n=1,2,...) 且有下界,那么极限 limn→∞an\lim \limits_{n \to \infty}a_nn→∞liman 存在。
2. 直观理解
单调有界定理的直观解释是:如果一个数列单调递增且有上界(或单调递减且有下界),那么它的项将会"堆积"在某一点附近,这个点就是该数列的极限。
3. Python代码验证
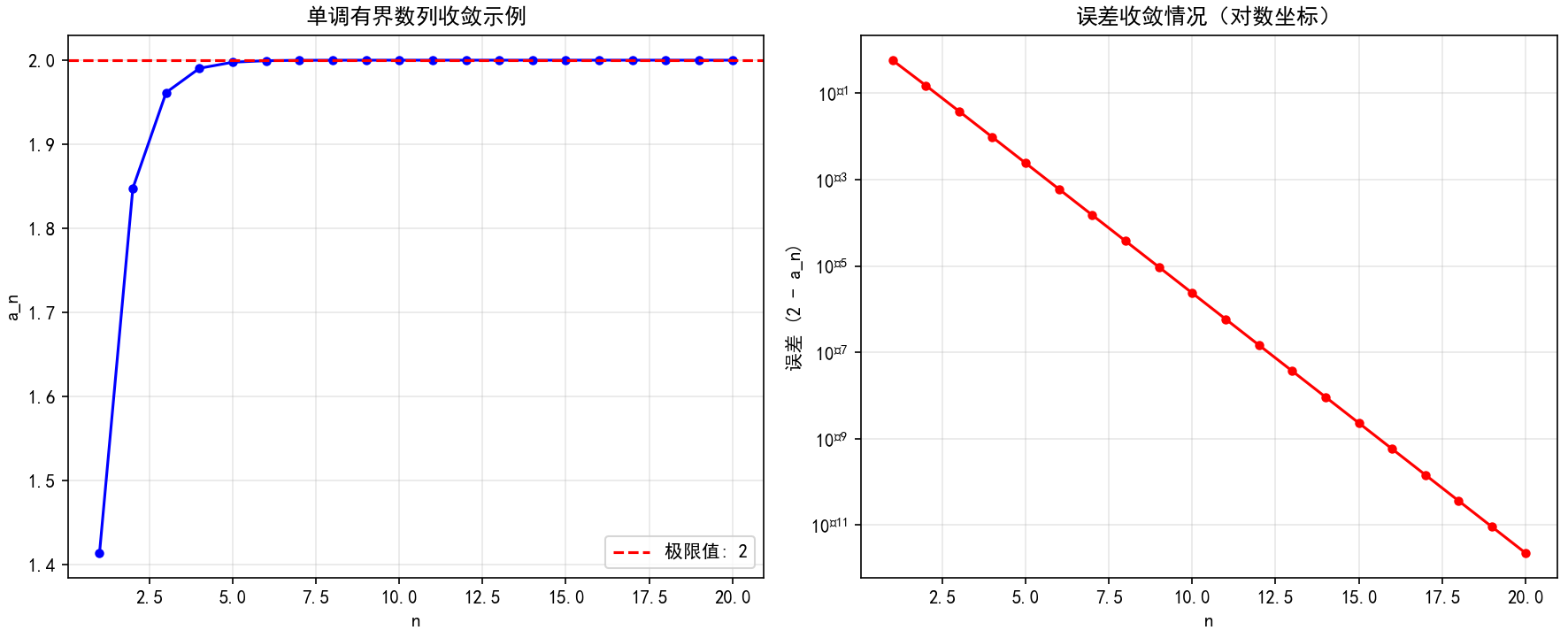
考虑数列 a1=2a_1 = \sqrt{2}a1=2 , a2=2+2a_2 = \sqrt{2+\sqrt{2}}a2=2+2 , a3=2+2+2a_3 = \sqrt{2+\sqrt{2+\sqrt{2}}}a3=2+2+2 , ...,即 an+1=2+ana_{n+1} = \sqrt{2 + a_n}an+1=2+an 。我们可以用Python验证这个数列的收敛性。
python
import numpy as np
import matplotlib.pyplot as plt
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def recursive_sequence(n_terms):
"""
计算递归定义的数列: a_{n+1} = sqrt(2 + a_n), a_1 = sqrt(2)
"""
sequence = [np.sqrt(2)] # a1
for i in range(1, n_terms):
next_term = np.sqrt(2 + sequence[-1])
sequence.append(next_term)
return sequence
# 计算前20项
n_terms = 20
sequence = recursive_sequence(n_terms)
# 绘制数列收敛情况
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(range(1, n_terms+1), sequence, 'bo-', markersize=4)
plt.axhline(y=2, color='r', linestyle='--', label='极限值: 2')
plt.xlabel('n')
plt.ylabel('a_n')
plt.title('单调有界数列收敛示例')
plt.legend()
plt.grid(True, alpha=0.3)
# 计算误差(与极限值的差)
errors = [2 - term for term in sequence]
plt.subplot(1, 2, 2)
plt.semilogy(range(1, n_terms+1), errors, 'ro-', markersize=4)
plt.xlabel('n')
plt.ylabel('误差 (2 - a_n)')
plt.title('误差收敛情况(对数坐标)')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 输出前几项和最后几项
print("数列前10项:")
for i in range(min(10, n_terms)):
print(f"a_{i+1} = {sequence[i]:.10f}")
print("\n数列最后5项:")
for i in range(max(0, n_terms-5), n_terms):
print(f"a_{i+1} = {sequence[i]:.10f}")
# 验证单调性和有界性
is_increasing = all(sequence[i] <= sequence[i+1] for i in range(len(sequence)-1))
is_bounded = all(term < 2 for term in sequence)
print(f"\n数列单调递增: {is_increasing}")
print(f"数列有上界(所有项 < 2): {is_bounded}")
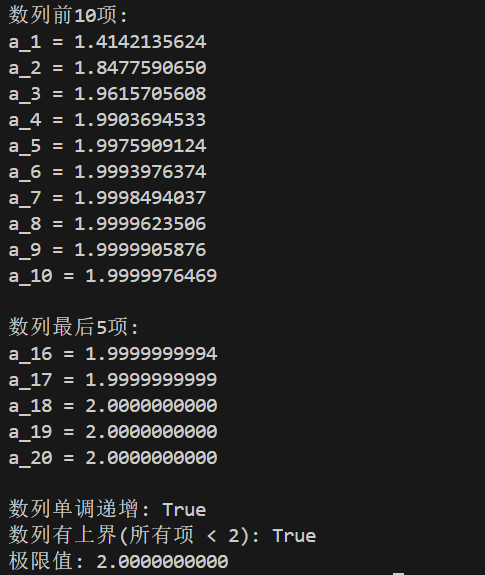
print(f"极限值: {sequence[-1]:.10f}")运行此代码,我们可以清晰地看到数列单调递增且以2为上界,逐渐收敛于2。
4. 实际应用示例
例题 :设 0<x1<π0 < x_1 < \pi0<x1<π,xn+1=sinxnx_{n+1} = \sin x_nxn+1=sinxn (n=1,2,3,⋯n=1,2,3,\cdotsn=1,2,3,⋯),证明 limxn\lim x_nlimxn 存在并求出该极限。
解 :首先证明数列有界:由于 0<x1<π0 < x_1 < \pi0<x1<π,则 0<x2=sinx1≤1<π0 < x_2 = \sin x_1 \leq 1 < \pi0<x2=sinx1≤1<π,同理可推得 0<xn+1=sinxn≤1<π0 < x_{n+1} = \sin x_n \leq 1 < \pi0<xn+1=sinxn≤1<π,因此数列有界。
再证明数列单调:因为当 x>0x > 0x>0 时,sinx<x\sin x < xsinx<x,所以 xn+1xn=sinxnxn<1\frac{x_{n+1}}{x_n} = \frac{\sin x_n}{x_n} < 1xnxn+1=xnsinxn<1,即 xn+1<xnx_{n+1} < x_nxn+1<xn,数列单调递减。
因此由单调有界定理,极限存在。设 limxn=a\lim x_n = alimxn=a,在 xn+1=sinxnx_{n+1} = \sin x_nxn+1=sinxn 两边取极限得 a=sinaa = \sin aa=sina,解得 a=0a = 0a=0。
🔍 探索实验
修改上面代码中的初始值,观察数列的收敛性是否改变?尝试不同的初始值(如0.5, 1.0, 2.0),看看收敛速度和极限值是否有变化?
三、两个定理的比较与应用场景
1. 异同点对比
| 特征 | 夹逼定理 | 单调有界定理 |
|---|---|---|
| 适用对象 | 函数、数列 | 主要适用于数列 |
| 主要功能 | 求极限值 | 证明极限存在性 |
| 使用条件 | 需要找到上下界函数 | 需要证明单调性和有界性 |
| 优势 | 可以直接求出极限值 | 不需要知道极限值即可证明存在性 |
2. 应用技巧总结
-
夹逼定理的应用技巧:
- 对于复杂的函数,尝试找到两个简单的函数作为上下界
- 上下界函数应该具有相同的极限
- 特别适用于含有三角函数、指数函数等复杂结构的极限问题
-
单调有界定理的应用技巧:
- 证明单调性:通常使用差分法(an+1−ana_{n+1} - a_nan+1−an)或比值法(an+1/ana_{n+1}/a_nan+1/an)
- 证明有界性:使用数学归纳法或不等式技巧
- 适用于递归定义的数列
四、进阶应用:两个定理的结合使用
在实际问题中,两个定理常常结合使用。例如,先使用单调有界定理证明极限存在,再使用夹逼定理或其他方法求出具体的极限值。
python
import numpy as np
import matplotlib.pyplot as plt
import math
def calculate_e_with_theorems():
"""
使用夹逼定理和单调有界定理计算自然常数e
"""
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 创建图形
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# 参数设置
n_max = 100
n_values = np.arange(1, n_max + 1)
# 定义两个关键数列
# a_n = (1 + 1/n)^n 单调递增
# b_n = (1 + 1/n)^(n+1) 单调递减
a_n = (1 + 1/n_values)**n_values
b_n = (1 + 1/n_values)**(n_values + 1)
# 真实e值
e_true = math.e
print("=" * 60)
print("使用夹逼定理和单调有界定理计算自然常数e")
print("=" * 60)
# 验证夹逼定理条件
print("\n1. 夹逼定理验证:")
print(" - 夹条件:a_n ≤ e ≤ b_n 对所有n成立")
print(" - 逼条件:lim(n→∞) a_n = lim(n→∞) b_n = e")
print(" 因此,根据夹逼定理,e = lim(n→∞) a_n = lim(n→∞) b_n")
# 验证单调有界定理条件
print("\n2. 单调有界定理验证:")
print(" - a_n 单调递增:a_{n+1} ≥ a_n")
print(" - b_n 单调递减:b_{n+1} ≤ b_n")
print(" - a_n 有上界:a_n ≤ b_n ≤ 4")
print(" - b_n 有下界:b_n ≥ a_n ≥ 2")
print(" 根据单调有界定理,两个数列均收敛")
# 在第一个子图上绘制夹逼定理
ax1.plot(n_values, a_n, 'b-', label=r'$a_n = (1 + \frac{1}{n})^n$ (递增)', linewidth=2)
ax1.plot(n_values, b_n, 'r-', label=r'$b_n = (1 + \frac{1}{n})^{n+1}$ (递减)', linewidth=2)
ax1.axhline(y=e_true, color='green', linestyle='--',
label=f'真实值 e ≈ {e_true:.10f}', linewidth=2)
# 标记夹逼区间
for n in [1, 5, 10, 20]:
ax1.plot([n, n], [a_n[n-1], b_n[n-1]], 'k-', alpha=0.3)
ax1.set_title('夹逼定理:a_n ≤ e ≤ b_n')
ax1.set_xlabel('n')
ax1.set_ylabel('函数值')
ax1.grid(True, linestyle='--', alpha=0.7)
ax1.legend()
ax1.set_ylim(2.5, 3.0)
# 在第二个子图上展示误差收敛
a_error = np.abs(a_n - e_true)
b_error = np.abs(b_n - e_true)
interval_width = b_n - a_n
ax2.semilogy(n_values, a_error, 'b-', label=r'$|a_n - e|$', linewidth=2)
ax2.semilogy(n_values, b_error, 'r-', label=r'$|b_n - e|$', linewidth=2)
ax2.semilogy(n_values, interval_width, 'g-', label='夹逼区间宽度', linewidth=2)
ax2.set_title('误差分析和收敛速度')
ax2.set_xlabel('n')
ax2.set_ylabel('误差(对数坐标)')
ax2.grid(True, linestyle='--', alpha=0.7)
ax2.legend()
plt.tight_layout()
plt.show()
# 数值计算结果
print("\n3. 数值计算结果:")
print("-" * 60)
print(f"真实值 e = {e_true:.15f}")
print("\nn\t a_n\t\t\t b_n\t\t\t 区间宽度\t a_n误差")
print("-" * 90)
test_n = [1, 5, 10, 50, 100, 1000]
for n in test_n:
a_val = (1 + 1/n)**n
b_val = (1 + 1/n)**(n+1)
width = b_val - a_val
a_err = abs(a_val - e_true)
print(f"{n}\t {a_val:.10f}\t {b_val:.10f}\t {width:.2e}\t {a_err:.2e}")
# 验证单调性
print("\n4. 单调性验证:")
print("-" * 60)
# 验证a_n单调递增
a_monotonic = all(a_n[i] <= a_n[i+1] for i in range(len(a_n)-1))
b_monotonic = all(b_n[i] >= b_n[i+1] for i in range(len(b_n)-1))
print(f"a_n 单调递增: {a_monotonic}")
print(f"b_n 单调递减: {b_monotonic}")
# 验证夹逼条件
squeeze_condition = all(a_n[i] <= e_true <= b_n[i] for i in range(len(a_n)))
print(f"夹逼条件满足 (a_n ≤ e ≤ b_n): {squeeze_condition}")
# 计算极限近似值
print("\n5. 极限计算结果:")
print("-" * 60)
# 使用较大的n计算极限近似值
large_n = 1000000
e_approx = (1 + 1/large_n)**large_n
error = abs(e_approx - e_true)
print(f"使用 n = {large_n} 计算:")
print(f"近似值: {e_approx:.15f}")
print(f"真实值: {e_true:.15f}")
print(f"绝对误差: {error:.2e}")
print(f"相对误差: {error/e_true:.2%}")
def theoretical_proof():
"""
定理的数学证明概要
"""
print("\n" + "=" * 60)
print("数学证明概要")
print("=" * 60)
print("""
1. 单调有界定理证明:
- 使用二项式定理展开 a_n = (1 + 1/n)^n
- 证明每一项都是非负且递增的
- 证明数列有上界(如 3)
- 因此极限存在
1. 夹逼定理证明:
- 构造不等式:a_n ≤ e ≤ b_n
- 证明 lim(n→∞) (b_n - a_n) = 0
- 因此 lim(n→∞) a_n = lim(n→∞) b_n = e
1. 极限计算:
e = lim(n→∞) (1 + 1/n)^n
= 1 + 1/1! + 1/2! + 1/3! + ... (泰勒级数展开)
""")
if __name__ == "__main__":
calculate_e_with_theorems()
theoretical_proof()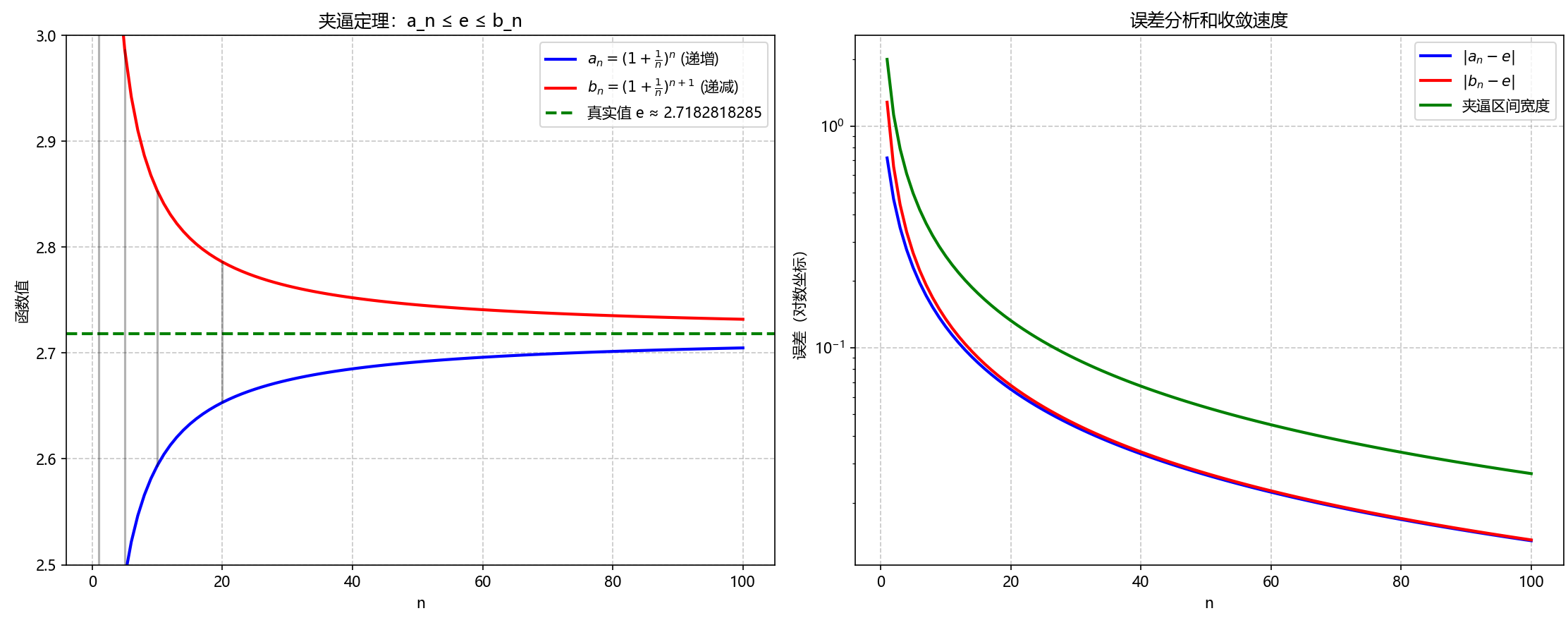
五、总结
夹逼定理和单调有界收敛定理是微积分中两大基础性定理,它们分别从不同角度解决了极限的存在性问题。
夹逼定理 通过构建不等式关系,让我们能够通过已知函数的极限来确定复杂函数的极限。它的核心思想是"夹逼",即通过上下两个边界函数来控制目标函数的行为。
单调有界收敛定理 则从数列本身的性质出发,指出单调且有界的数列必然收敛。这一定理的价值在于,即使我们不知道极限的具体值,也能判定极限的存在性。
在实际应用中,两个定理常常结合使用,单调有界定理保证极限存在,而夹逼定理或其他方法则用于求出具体的极限值。掌握这两个定理,对于深入理解微积分和数学分析的基本概念至关重要。
📚 进一步学习建议
- 理论深化:学习柯西收敛准则,这是更一般的收敛判定方法
- 应用拓展:研究这两个定理在数值分析、优化算法等领域的应用
- 编程实践:尝试用Python实现更复杂的极限计算和收敛性判断算法
通过本文的数学理论阐述和Python代码示例,希望读者能够直观理解这两个重要定理的内涵和应用方法,为后续的微积分学习打下坚实基础。
思考题:你能举出一个需要同时使用这两个定理的实际例子吗?欢迎在评论区分享你的想法!
参考资料:
- 扈志明,《微积分》,高等教育出版社
欢迎点赞、收藏、评论,您的支持是我持续创作的最大动力!如有任何疑问,欢迎在评论区提出,我会尽快解答。。