参数曲线切向量与叉乘向量的精确计算与分析

在几何建模和计算机图形学中，参数曲线的切向量计算是一个基础而重要的问题。本文将详细探讨如何使用符号计算和解析方法精确计算复杂参数曲线的单位切向量，并分析其与固定向量的叉乘结果。

问题描述与数学模型

我们考虑一条由五个分段组成的平面曲线，位于Y-Z平面上（X坐标恒为0）。这五个分段分别为：

• p f 1 pf1 pf1：直线段，参数为 t t t，从 r r r到 0 0 0
• p a 1 pa1 pa1：圆弧段，参数为 θ \theta θ，从 π 2 + d A − d B \frac{\pi}{2}+dA-dB 2π+dA−dB到 π 2 + d A \frac{\pi}{2}+dA 2π+dA
• p f 2 pf2 pf2：直线段，参数为 t t t，从 d s ds ds到 0 0 0
• p a 2 pa2 pa2：圆弧段，参数为 θ \theta θ，从 − π 2 + d A -\frac{\pi}{2}+dA −2π+dA到 − π 2 + d A − d C -\frac{\pi}{2}+dA-dC −2π+dA−dC
• p b a c k pback pback：直线段，参数为 t t t，从 0 0 0到 r r r

其中各个符号的含义如下：

• d A , d B , d C dA, dB, dC dA,dB,dC：角度参数
• r 2 , r 3 r2, r3 r2,r3：圆弧半径
• d s , d z , d d ds, dz, dd ds,dz,dd：位移参数
• r r r：参考圆半径

各段的参数方程如下：

pf1段 ：
p f 1 = [ 0 ( d s − d z ) cos ⁡ ( d A ) + r 2 sin ⁡ ( d A ) + r 2 cos ⁡ ( π 2 + d A − d B ) + t sin ⁡ ( π 2 + d A − d B ) − ( d s − d z ) sin ⁡ ( d A ) + r 2 cos ⁡ ( d A ) − r 2 sin ⁡ ( π 2 + d A − d B ) + t cos ⁡ ( π 2 + d A − d B ) ] pf1 = \begin{bmatrix} 0 \\ (ds-dz)\cos(dA)+r2\sin(dA)+r2\cos(\frac{\pi}{2}+dA-dB)+t\sin(\frac{\pi}{2}+dA-dB) \\ -(ds-dz)\sin(dA)+r2\cos(dA)-r2\sin(\frac{\pi}{2}+dA-dB)+t\cos(\frac{\pi}{2}+dA-dB) \end{bmatrix} pf1= 0(ds−dz)cos(dA)+r2sin(dA)+r2cos(2π+dA−dB)+tsin(2π+dA−dB)−(ds−dz)sin(dA)+r2cos(dA)−r2sin(2π+dA−dB)+tcos(2π+dA−dB)

pa1段 ：
p a 1 = [ 0 ( d s − d z ) cos ⁡ ( d A ) + r 2 sin ⁡ ( d A ) + r 2 cos ⁡ ( θ ) − ( d s − d z ) sin ⁡ ( d A ) + r 2 cos ⁡ ( d A ) − r 2 sin ⁡ ( θ ) ] pa1 = \begin{bmatrix} 0 \\ (ds-dz)\cos(dA)+r2\sin(dA)+r2\cos(\theta) \\ -(ds-dz)\sin(dA)+r2\cos(dA)-r2\sin(\theta) \end{bmatrix} pa1= 0(ds−dz)cos(dA)+r2sin(dA)+r2cos(θ)−(ds−dz)sin(dA)+r2cos(dA)−r2sin(θ)

pf2段 ：
p f 2 = [ 0 t cos ⁡ ( d A ) − t sin ⁡ ( d A ) ] pf2 = \begin{bmatrix} 0 \\ t\cos(dA) \\ -t\sin(dA) \end{bmatrix} pf2= 0tcos(dA)−tsin(dA)

pa2段 ：
p a 2 = [ 0 − r 3 sin ⁡ ( d A ) + r 3 cos ⁡ ( θ ) − r 3 cos ⁡ ( d A ) − r 3 sin ⁡ ( θ ) ] pa2 = \begin{bmatrix} 0 \\ -r3\sin(dA)+r3\cos(\theta) \\ -r3\cos(dA)-r3\sin(\theta) \end{bmatrix} pa2= 0−r3sin(dA)+r3cos(θ)−r3cos(dA)−r3sin(θ)

pback段 ：
p b a c k = [ 0 − r 3 sin ⁡ ( d A ) + r 3 cos ⁡ ( − π 2 + d A − d C ) + t sin ⁡ ( − π 2 + d A − d C ) − r 3 cos ⁡ ( d A ) − r 3 sin ⁡ ( − π 2 + d A − d C ) + t cos ⁡ ( − π 2 + d A − d C ) ] pback = \begin{bmatrix} 0 \\ -r3\sin(dA)+r3\cos(-\frac{\pi}{2}+dA-dC)+t\sin(-\frac{\pi}{2}+dA-dC) \\ -r3\cos(dA)-r3\sin(-\frac{\pi}{2}+dA-dC)+t\cos(-\frac{\pi}{2}+dA-dC) \end{bmatrix} pback= 0−r3sin(dA)+r3cos(−2π+dA−dC)+tsin(−2π+dA−dC)−r3cos(dA)−r3sin(−2π+dA−dC)+tcos(−2π+dA−dC)

切向量的精确计算方法

数值微分法的局限性

传统的数值微分方法通过离散点的差分来近似计算切向量：
T ⃗ ≈ r ⃗ ( t + Δ t ) − r ⃗ ( t ) Δ t \vec{T} \approx \frac{\vec{r}(t+\Delta t) - \vec{r}(t)}{\Delta t} T ≈Δtr (t+Δt)−r (t)

这种方法虽然简单，但会引入截断误差和舍入误差，特别是在曲率变化较大的区域。对于高精度要求的应用，这种近似方法往往不够理想。

解析导数法的优势

我们采用符号计算方法，直接对参数方程求导，得到精确的切向量表达式。对于参数方程 r ⃗ ( t ) = ( x ( t ) , y ( t ) , z ( t ) ) \vec{r}(t) = (x(t), y(t), z(t)) r (t)=(x(t),y(t),z(t))，其切向量为：
T ⃗ = d r ⃗ d t = ( d x d t , d y d t , d z d t ) \vec{T} = \frac{d\vec{r}}{dt} = \left(\frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt}\right) T =dtdr =(dtdx,dtdy,dtdz)

使用SymPy库，我们可以直接计算各段参数方程的导数：

pf1_tangent = sy.diff(pf1_sub, t)
pa1_tangent = sy.diff(pa1_sub, theta)
pf2_tangent = sy.diff(pf2_sub, t)
pa2_tangent = sy.diff(pa2_sub, theta)
pb_tangent = sy.diff(pb_sub, t)

这种方法完全避免了数值误差，提供了数学上精确的切向量。

切向量方向的一致性保证

确保各段切向量方向一致是计算中的关键问题。我们根据参数的变化方向决定是否需要反转切向量：

• p f 1 pf1 pf1段：参数 t t t从 r r r到 0 0 0（递减），需要反转切向量
• p a 1 pa1 pa1段：参数 θ \theta θ从 π 2 + d A − d B \frac{\pi}{2}+dA-dB 2π+dA−dB到 π 2 + d A \frac{\pi}{2}+dA 2π+dA（递增），保持原方向
• p f 2 pf2 pf2段：参数 t t t从 d s ds ds到 0 0 0（递减），需要反转切向量
• p a 2 pa2 pa2段：参数 θ \theta θ从 − π 2 + d A -\frac{\pi}{2}+dA −2π+dA到 − π 2 + d A − d C -\frac{\pi}{2}+dA-dC −2π+dA−dC（递减），需要反转切向量
• p b a c k pback pback段：参数 t t t从 0 0 0到 r r r（递增），保持原方向

通过引入reverse_direction参数，我们可以灵活控制各段切向量的方向：

def compute_unit_tangent(tangent_expr, param, param_values, reverse_direction=False):
    # ... 计算切向量分量 ...
    
    # 如果需要反转方向
    if reverse_direction:
        tx = -tx
        ty = -ty
        tz = -tz
    
    # 单位化 ...
    return tx, ty, tz

叉乘向量的计算与分析

叉乘的数学定义

给定两个三维向量 a ⃗ = ( a x , a y , a z ) \vec{a} = (a_x, a_y, a_z) a =(ax,ay,az)和 b ⃗ = ( b x , b y , b z ) \vec{b} = (b_x, b_y, b_z) b =(bx,by,bz)，它们的叉乘定义为：
a ⃗ × b ⃗ = ( a y b z − a z b y , a z b x − a x b z , a x b y − a y b x ) \vec{a} \times \vec{b} = (a_y b_z - a_z b_y, a_z b_x - a_x b_z, a_x b_y - a_y b_x) a ×b =(aybz−azby,azbx−axbz,axby−aybx)

在我们的问题中， a ⃗ = ( 1 , 0 , 0 ) \vec{a} = (1, 0, 0) a =(1,0,0)是固定向量， b ⃗ = T ⃗ \vec{b} = \vec{T} b =T 是单位切向量。

叉乘的几何意义

向量 a ⃗ × b ⃗ \vec{a} \times \vec{b} a ×b 的结果是一个垂直于 a ⃗ \vec{a} a 和 b ⃗ \vec{b} b 所在平面的向量，其方向由右手定则确定，大小等于 ∣ a ⃗ ∣ ∣ b ⃗ ∣ sin ⁡ θ |\vec{a}||\vec{b}|\sin\theta ∣a ∣∣b ∣sinθ，其中 θ \theta θ是两向量间的夹角。

由于 a ⃗ = ( 1 , 0 , 0 ) \vec{a} = (1, 0, 0) a =(1,0,0)且曲线位于Y-Z平面（X=0），叉乘结果实际上表示了曲线法向量的方向。在二维情况下，这相当于计算曲线的法向量。

叉乘结果的计算

在我们的实现中，叉乘计算如下：

# 计算叉乘: (1,0,0) × (tx, ty, tz)
cross_x = unit_vec_y * tz_all - unit_vec_z * ty_all
cross_y = unit_vec_z * tx_all - unit_vec_x * tz_all
cross_z = unit_vec_x * ty_all - unit_vec_y * tx_all

由于 a ⃗ = ( 1 , 0 , 0 ) \vec{a} = (1, 0, 0) a =(1,0,0)，计算可以简化为：
a ⃗ × T ⃗ = ( 0 ⋅ T z − 0 ⋅ T y , 0 ⋅ T x − 1 ⋅ T z , 1 ⋅ T y − 0 ⋅ T x ) = ( 0 , − T z , T y ) \vec{a} \times \vec{T} = (0 \cdot T_z - 0 \cdot T_y, 0 \cdot T_x - 1 \cdot T_z, 1 \cdot T_y - 0 \cdot T_x) = (0, -T_z, T_y) a ×T =(0⋅Tz−0⋅Ty,0⋅Tx−1⋅Tz,1⋅Ty−0⋅Tx)=(0,−Tz,Ty)

这一结果清晰地显示了叉乘向量的Y和Z分量直接由切向量的Z和Y分量决定，但符号相反。

可视化与分析

坐标系设置

我们将坐标系设置为Z轴水平向右、Y轴竖直向上，这与传统的数学坐标系一致，便于直观理解曲线的几何特性。

参考圆的绘制

为了提供空间参考，我们绘制了一个半径为 r r r的圆：
c i r c l e z = r ⋅ cos ⁡ ( θ ) circle_z = r \cdot \cos(\theta) circlez=r⋅cos(θ)
c i r c l e y = r ⋅ sin ⁡ ( θ ) circle_y = r \cdot \sin(\theta) circley=r⋅sin(θ)

其中 θ \theta θ从 0 0 0到 2 π 2\pi 2π。

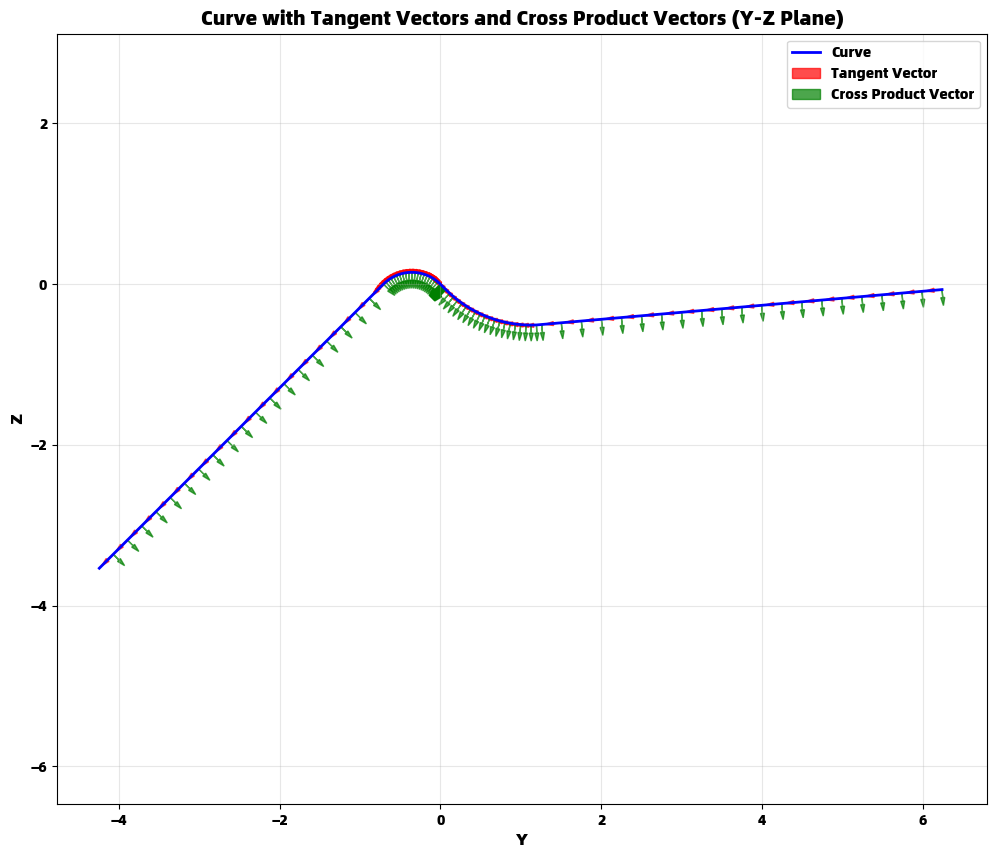
向量可视化

我们使用箭头表示切向量和叉乘向量：

• 红色箭头：单位切向量 T ⃗ \vec{T} T
• 绿色箭头：叉乘向量 a ⃗ × T ⃗ \vec{a} \times \vec{T} a ×T

通过适当选择箭头密度和大小，我们可以在保持图形清晰的同时展示向量的变化趋势。

数学分析与化简

切向量的解析表达式

通过符号计算，我们可以得到各段切向量的精确表达式。以 p f 2 pf2 pf2段为例：
r ⃗ p f 2 ( t ) = ( 0 , t cos ⁡ ( d A ) , − t sin ⁡ ( d A ) ) \vec{r}_{pf2}(t) = (0, t\cos(dA), -t\sin(dA)) r pf2(t)=(0,tcos(dA),−tsin(dA))

对其求导：
T ⃗ p f 2 = d r ⃗ p f 2 d t = ( 0 , cos ⁡ ( d A ) , − sin ⁡ ( d A ) ) \vec{T}{pf2} = \frac{d\vec{r}{pf2}}{dt} = (0, \cos(dA), -\sin(dA)) T pf2=dtdr pf2=(0,cos(dA),−sin(dA))

这是一个常向量，表明 p f 2 pf2 pf2段是直线段，切向量方向恒定。

叉乘结果的三角恒等式应用

对于叉乘结果 a ⃗ × T ⃗ = ( 0 , − T z , T y ) \vec{a} \times \vec{T} = (0, -T_z, T_y) a ×T =(0,−Tz,Ty)，我们可以利用三角恒等式进一步分析其性质。

考虑 p a 1 pa1 pa1段的切向量：
T ⃗ p a 1 = d r ⃗ p a 1 d θ = ( 0 , − r 2 sin ⁡ ( θ ) , − r 2 cos ⁡ ( θ ) ) \vec{T}{pa1} = \frac{d\vec{r}{pa1}}{d\theta} = (0, -r2\sin(\theta), -r2\cos(\theta)) T pa1=dθdr pa1=(0,−r2sin(θ),−r2cos(θ))

则叉乘结果为：
a ⃗ × T ⃗ p a 1 = ( 0 , r 2 cos ⁡ ( θ ) , − r 2 sin ⁡ ( θ ) ) \vec{a} \times \vec{T}_{pa1} = (0, r2\cos(\theta), -r2\sin(\theta)) a ×T pa1=(0,r2cos(θ),−r2sin(θ))

利用三角函数的积化和差公式，我们可以分析叉乘向量分量的相互关系。对于任意角度 α \alpha α和 β \beta β，有：
cos ⁡ α sin ⁡ β = 1 2 [ sin ⁡ ( α + β ) − sin ⁡ ( α − β ) ] \cos\alpha\sin\beta = \frac{1}{2}[\sin(\alpha+\beta) - \sin(\alpha-\beta)] cosαsinβ=21[sin(α+β)−sin(α−β)]
sin ⁡ α cos ⁡ β = 1 2 [ sin ⁡ ( α + β ) + sin ⁡ ( α − β ) ] \sin\alpha\cos\beta = \frac{1}{2}[\sin(\alpha+\beta) + \sin(\alpha-\beta)] sinαcosβ=21[sin(α+β)+sin(α−β)]

应用这些恒等式，我们可以将叉乘向量的分量表示为更简洁的形式。特别地，注意到：
( a ⃗ × T ⃗ p a 1 ) y = r 2 cos ⁡ ( θ ) (\vec{a} \times \vec{T}_{pa1})y = r2\cos(\theta) (a ×T pa1)y=r2cos(θ)
( a ⃗ × T ⃗ p a 1 ) z = − r 2 sin ⁡ ( θ ) (\vec{a} \times \vec{T}{pa1})_z = -r2\sin(\theta) (a ×T pa1)z=−r2sin(θ)

这两个分量满足：

( a ⃗ × T ⃗ p a 1 ) y \] 2 + \[ ( a ⃗ × T ⃗ p a 1 ) z \] 2 = r 2 2 ( cos ⁡ 2 θ + sin ⁡ 2 θ ) = r 2 2 \[(\\vec{a} \\times \\vec{T}_{pa1})_y\]\^2 + \[(\\vec{a} \\times \\vec{T}_{pa1})_z\]\^2 = r2\^2(\\cos\^2\\theta + \\sin\^2\\theta) = r2\^2 \[(a ×T pa1)y\]2+\[(a ×T pa1)z\]2=r22(cos2θ+sin2θ)=r22 这表明叉乘向量的Y和Z分量构成一个半径为 r 2 r2 r2的圆参数方程，这与其几何意义一致------叉乘向量垂直于切向量，而切向量本身在圆弧段上以恒定角速度旋转。 #### 一般情况下的叉乘向量分析 对于一般的切向量 T ⃗ = ( 0 , T y , T z ) \\vec{T} = (0, T_y, T_z) T =(0,Ty,Tz)，叉乘结果为 ( 0 , − T z , T y ) (0, -T_z, T_y) (0,−Tz,Ty)。其模长为： ∣ a ⃗ × T ⃗ ∣ = ( − T z ) 2 + ( T y ) 2 = T y 2 + T z 2 = 1 \|\\vec{a} \\times \\vec{T}\| = \\sqrt{(-T_z)\^2 + (T_y)\^2} = \\sqrt{T_y\^2 + T_z\^2} = 1 ∣a ×T ∣=(−Tz)2+(Ty)2 =Ty2+Tz2 =1 因为 T ⃗ \\vec{T} T 是单位切向量。这表明叉乘结果本身也是单位向量，这与我们的数值验证一致。 ### 结论 本文详细介绍了参数曲线切向量与叉乘向量的精确计算方法。通过使用符号计算和解析导数，我们避免了数值微分带来的误差，确保了计算结果的数学精确性。通过仔细处理各段切向量的方向一致性，我们保证了整个曲线上的切向量场是连续的。 叉乘计算的结果提供了曲线法向量的信息，在二维情况下，这相当于曲线的法向量场。通过三角恒等式的应用，我们进一步分析了叉乘向量的数学性质，揭示了其与原始曲线几何特性的内在联系。 这种方法不仅适用于本文讨论的特定曲线，还可以推广到更一般的参数曲线分析中，为几何建模、计算机图形学和物理仿真等领域提供可靠的数学工具。 **示例结果化简** ： 对于圆弧段 p a 1 pa1 pa1，切向量为 T ⃗ p a 1 = ( 0 , − r 2 sin ⁡ ( θ ) , − r 2 cos ⁡ ( θ ) ) \\vec{T}_{pa1} = (0, -r2\\sin(\\theta), -r2\\cos(\\theta)) T pa1=(0,−r2sin(θ),−r2cos(θ))，则叉乘结果为： a ⃗ × T ⃗ p a 1 = ( 0 , r 2 cos ⁡ ( θ ) , − r 2 sin ⁡ ( θ ) ) \\vec{a} \\times \\vec{T}_{pa1} = (0, r2\\cos(\\theta), -r2\\sin(\\theta)) a ×T pa1=(0,r2cos(θ),−r2sin(θ)) 利用积化和差公式，我们可以验证： \[ r 2 cos ⁡ ( θ ) \] 2 + \[ − r 2 sin ⁡ ( θ ) \] 2 = r 2 2 ( cos ⁡ 2 θ + sin ⁡ 2 θ ) = r 2 2 \[r2\\cos(\\theta)\]\^2 + \[-r2\\sin(\\theta)\]\^2 = r2\^2(\\cos\^2\\theta + \\sin\^2\\theta) = r2\^2 \[r2cos(θ)\]2+\[−r2sin(θ)\]2=r22(cos2θ+sin2θ)=r22 这表明叉乘向量的模长恒为 r 2 r2 r2，与我们的解析结果一致。