数据挖掘必会技能之:A/B测试
- 1、引言
- [2. A/B测试](#2. A/B测试)
-
- [2.1 了解A/B测试](#2.1 了解A/B测试)
-
- 2.1.1什么是A/B测试?
- [2.1.2 为什么需要A/B测试?](#2.1.2 为什么需要A/B测试?)
- [2.1.3 A/B测试的流程](#2.1.3 A/B测试的流程)
- [2.2 实施流程](#2.2 实施流程)
-
- [2.2.1 第一步:明确实验目标与假设](#2.2.1 第一步:明确实验目标与假设)
- [2.2.2 第二步:确定关键指标与样本量](#2.2.2 第二步:确定关键指标与样本量)
-
- [2.2.2.1 选择正确的指标](#2.2.2.1 选择正确的指标)
- [2.2.2.2 计算样本量](#2.2.2.2 计算样本量)
- [2.2.3 第三步:实验设计与实施](#2.2.3 第三步:实验设计与实施)
-
- [2.2.3.1 随机化与分流](#2.2.3.1 随机化与分流)
- [2.2.3.2 避免常见偏差](#2.2.3.2 避免常见偏差)
- [2.2.4 第四步:数据收集与监控](#2.2.4 第四步:数据收集与监控)
- [2.2.5 第五步:统计分析与结果解读](#2.2.5 第五步:统计分析与结果解读)
-
- [2.2.5.1 假设检验](#2.2.5.1 假设检验)
- [2.2.5.2 数据可视化](#2.2.5.2 数据可视化)
- [2.3 A/B测试的最佳实践与常见陷阱](#2.3 A/B测试的最佳实践与常见陷阱)
-
- [2.3.1 最佳实践](#2.3.1 最佳实践)
- [2.3.2 常见陷阱及避免方法](#2.3.2 常见陷阱及避免方法)
- 3、总结
1、引言
小屌丝 :鱼哥,我发现了!咱们APP昨天新上的那个"疯狂星期四"弹窗,点击率爆了,是旧版的整整两倍!这功能简直封神了!
小鱼 :(头也不抬,继续敲代码)哦?封神?那你再看看,今天的人均下单金额跌了多少。
小屌丝 :(快速滑动数据仪表盘,笑容逐渐凝固)呃......好像......跌了15%。不对啊,点击的人多了,怎么花钱还少了?
小鱼 :这就对了。你只看到一个地方"爆了",就像只看见人踮起脚,却不知道他是因为够着了果子,还是只是脚下踩了钉子。
小屌丝 :鱼哥,别卖关子了!那怎么才能知道,这新弹窗到底是"神助攻"还是"猪队友"?总不能凭感觉吧。

小鱼 :当然不能。在产品世界里,有一种方法,能让数据自己开口说话,告诉你哪个方案才是真英雄。
小屌丝 :(凑近)快说快说,什么方法这么神?
小鱼 :A/B测试。不玩虚的,不靠猜测,把用户"分"成两拨,一拨看旧弹窗(A组),一拨看新弹窗(B组),其他条件全都一样。最后,不是比谁"点击高",而是看哪一拨人最终带来的总收益高。
小屌丝 :我懂了!就像两拨种子,同样的阳光水土,就比谁结的果子多!那要是B组最后总营收赢了,新弹窗才算是真的赢,对吧?
小鱼 :悟性不错。否则,你可能会被一个华而不实的"高点击率"迷惑,上线一个实际上在悄悄赶走优质用户的"漏斗"。
小屌丝 :妙啊!那这A/B测试具体咋"分"咋"比"?里面有没有什么玄学,哦不,科学?
小鱼 :玄学没有,科学倒是一大堆。从怎么公平地"分流",到结果到底算不算"稳了",处处都是学问。想听?
小屌丝 :想!必须想!鱼哥,今天这堂《A/B测试》的硬核科普课,就指望你了!
小鱼:行,那咱们今天就掀开A/B测试的"神坛"面纱,看看它到底如何充当产品迭代的"公平裁判"。
2. A/B测试
2.1 了解A/B测试
2.1.1什么是A/B测试?
A/B测试(也称为分裂测试或对照实验)是一种通过将用户随机分配到不同实验组,比较各组的业务指标表现,从而确定哪个版本更优的实验方法。
核心思想:在控制其他变量不变的情况下,仅改变一个或多个实验因素,观察这些变化对用户行为的影响。
2.1.2 为什么需要A/B测试?
| 传统决策方式 | A/B测试决策方式 |
|---|---|
| 依赖直觉和经验 | 依赖数据证据 |
| 无法量化效果 | 精准测量影响程度 |
| 风险集中(全量发布) | 风险可控(小流量测试) |
| 难以归因(多因素混杂) | 清晰归因(单一变量) |

2.1.3 A/B测试的流程
为了便于理解,我整理思维导图
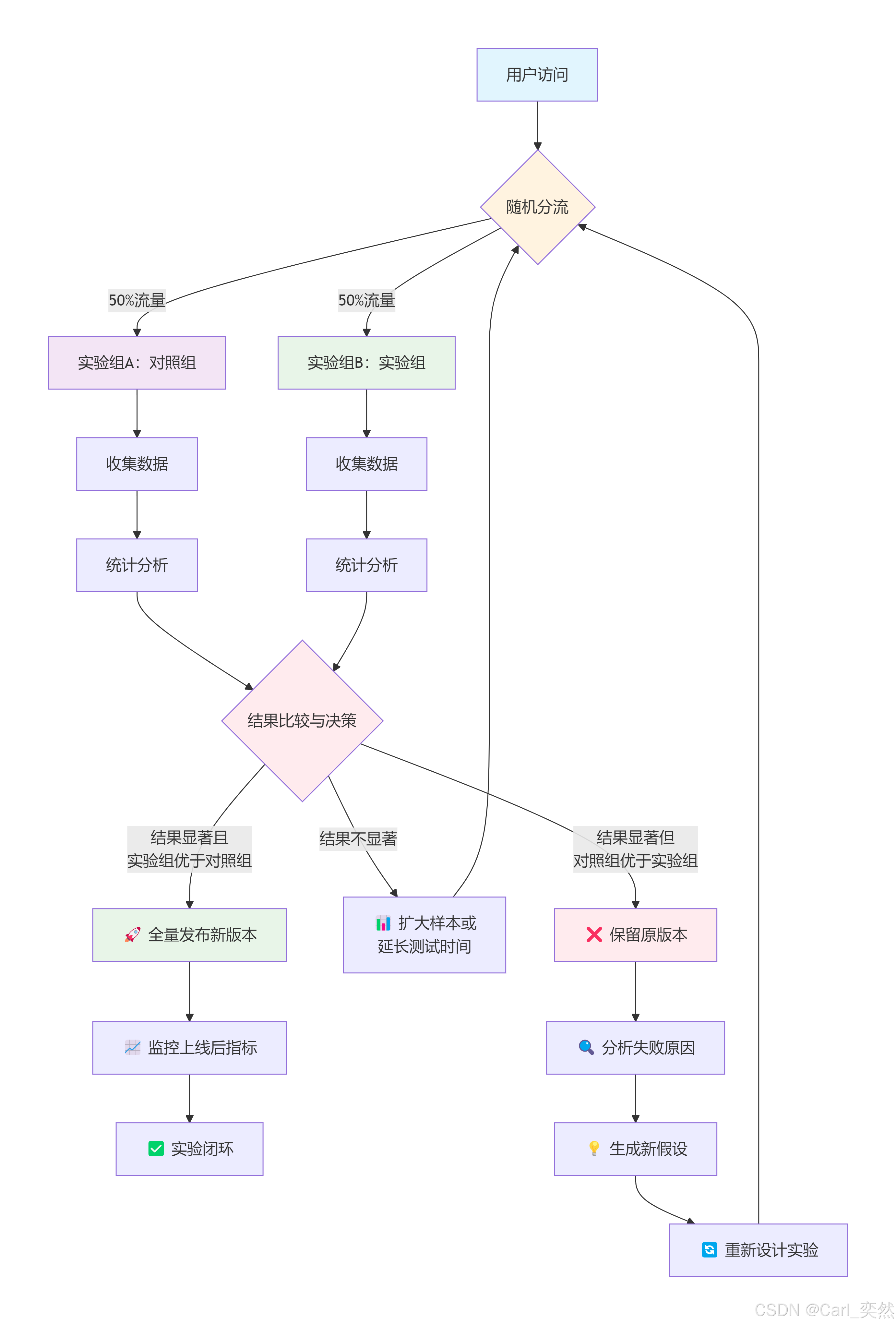
2.2 实施流程
2.2.1 第一步:明确实验目标与假设
在进行A/B测试前,必须明确三个核心问题:
- 我们要解决什么业务问题?
- 我们假设如何解决这个问题?
- 如何衡量解决方案的效果?
示例:
- 业务问题:商品详情页的转化率较低
- 假设:将"立即购买"按钮从蓝色改为红色,可以提高视觉吸引力,从而提升转化率
- 衡量指标:主要指标 - 按钮点击转化率;次要指标 - 页面停留时间、滚动深度
2.2.2 第二步:确定关键指标与样本量
2.2.2.1 选择正确的指标
- 主要指标:直接反映实验目标的指标(如转化率、收入)
- 次要指标:可能受影响的辅助指标(如页面停留时间、跳出率)
- 护栏指标:确保实验不会损害用户体验的监控指标(如崩溃率、投诉率)
2.2.2.2 计算样本量
样本量不足会导致统计功效不足,可能错过真实的效应;样本量过大则会浪费流量和延长实验时间。
python
import numpy as np
import scipy.stats as stats
def calculate_sample_size(alpha=0.05, power=0.8, p1=0.1, p2=0.12, ratio=1):
"""
计算A/B测试所需样本量
参数:
alpha: 显著性水平(第一类错误概率)
power: 统计功效(1 - 第二类错误概率)
p1: 对照组的转化率
p2: 实验组的预期转化率
ratio: 实验组与对照组的流量比例
返回:
每组所需样本量
"""
# 计算效应量
effect_size = abs(p2 - p1)
# 计算合并比例
p_pool = (p1 + p2 * ratio) / (1 + ratio)
# 计算Z值
z_alpha = stats.norm.ppf(1 - alpha/2) # 双尾检验
z_beta = stats.norm.ppf(power)
# 计算样本量
n = ((z_alpha * np.sqrt(p_pool * (1 - p_pool) * (1 + 1/ratio)) +
z_beta * np.sqrt(p1 * (1 - p1) + p2 * (1 - p2)/ratio)) ** 2) / (effect_size ** 2)
return int(np.ceil(n))
# 示例:计算样本量
p1 = 0.10 # 对照组当前转化率10%
p2 = 0.12 # 期望实验组提升到12%
alpha = 0.05
power = 0.8
sample_size = calculate_sample_size(alpha, power, p1, p2)
print(f"每组所需样本量: {sample_size}")
print(f"实验组总样本量: {sample_size * 2}")2.2.3 第三步:实验设计与实施
2.2.3.1 随机化与分流
确保用户随机分配到实验组和对照组,避免选择偏差。
python
import hashlib
import pandas as pd
def assign_to_group(user_id, salt='ab_test_salt', groups=['A', 'B'], weights=[0.5, 0.5]):
"""
基于用户ID将用户随机分配到实验组
参数:
user_id: 用户唯一标识
salt: 加盐值,增加随机性
groups: 实验组列表
weights: 各组流量比例
返回:
分配的实验组
"""
# 将用户ID和盐值结合
user_salt = str(user_id) + salt
# 计算哈希值
hash_value = hashlib.md5(user_salt.encode()).hexdigest()
# 将哈希值转换为0-1之间的浮点数
hash_int = int(hash_value, 16)
normalized_value = (hash_int % 10000) / 10000.0
# 根据权重分配组别
cumulative_weight = 0
for i, weight in enumerate(weights):
cumulative_weight += weight
if normalized_value < cumulative_weight:
return groups[i]
return groups[-1] # 默认返回最后一组
# 测试分流函数
test_user_ids = [12345, 67890, 11223, 44556, 77889]
for user_id in test_user_ids:
group = assign_to_group(user_id)
print(f"用户 {user_id} 被分配到组: {group}")
# 验证分流均匀性
def test_group_allocation(num_users=10000):
"""测试分组均匀性"""
allocations = {'A': 0, 'B': 0}
for i in range(num_users):
group = assign_to_group(i)
allocations[group] += 1
print(f"总用户数: {num_users}")
print(f"A组用户数: {allocations['A']} ({allocations['A']/num_users*100:.2f}%)")
print(f"B组用户数: {allocations['B']} ({allocations['B']/num_users*100:.2f}%)")
# 卡方检验
from scipy.stats import chisquare
observed = [allocations['A'], allocations['B']]
expected = [num_users/2, num_users/2]
chi2, p_value = chisquare(observed, expected)
print(f"卡方检验结果: χ² = {chi2:.4f}, p = {p_value:.4f}")
if p_value > 0.05:
print("结论: 分组是均匀的")
else:
print("警告: 分组可能不均匀")
test_group_allocation()2.2.3.2 避免常见偏差
- 新鲜感偏差:用户对新功能的好奇心导致短期行为改变
- 季节偏差:节假日、周末等时间因素影响用户行为
- 学习效应:用户逐渐适应新功能
- 实验污染:实验组用户与对照组用户交流
2.2.4 第四步:数据收集与监控
python
import time
from datetime import datetime, timedelta
import random
class ABTestDataCollector:
"""A/B测试数据收集器"""
def __init__(self, experiment_id, variant_a_name='control', variant_b_name='treatment'):
self.experiment_id = experiment_id
self.variant_a_name = variant_a_name
self.variant_b_name = variant_b_name
self.data = {
variant_a_name: {'users': set(), 'conversions': 0, 'sessions': 0},
variant_b_name: {'users': set(), 'conversions': 0, 'sessions': 0}
}
self.start_time = datetime.now()
def log_event(self, user_id, variant, event_type, timestamp=None):
"""记录用户事件"""
if timestamp is None:
timestamp = datetime.now()
if variant not in self.data:
raise ValueError(f"未知的实验组: {variant}")
# 记录用户
self.data[variant]['users'].add(user_id)
# 记录会话
if event_type == 'session_start':
self.data[variant]['sessions'] += 1
# 记录转化
elif event_type == 'conversion':
self.data[variant]['conversions'] += 1
return {
'experiment_id': self.experiment_id,
'user_id': user_id,
'variant': variant,
'event_type': event_type,
'timestamp': timestamp
}
def get_summary(self):
"""获取实验数据摘要"""
summary = {}
for variant, stats in self.data.items():
user_count = len(stats['users'])
conversion_rate = stats['conversions'] / stats['sessions'] if stats['sessions'] > 0 else 0
summary[variant] = {
'unique_users': user_count,
'total_sessions': stats['sessions'],
'total_conversions': stats['conversions'],
'conversion_rate': conversion_rate
}
return summary
def print_real_time_dashboard(self, interval_seconds=10, duration_minutes=5):
"""实时监控面板"""
end_time = datetime.now() + timedelta(minutes=duration_minutes)
print(f"\n{'='*60}")
print(f"A/B测试实时监控面板 - 实验ID: {self.experiment_id}")
print(f"{'='*60}")
print(f"开始时间: {self.start_time}")
print(f"预计结束时间: {end_time}")
print(f"{'='*60}\n")
while datetime.now() < end_time:
summary = self.get_summary()
print(f"\n更新时间: {datetime.now().strftime('%Y-%m-%d %H:%M:%S')}")
print(f"{'-'*60}")
for variant, stats in summary.items():
print(f"实验组: {variant}")
print(f" 独立用户数: {stats['unique_users']:6d}")
print(f" 总会话数: {stats['total_sessions']:6d}")
print(f" 总转化数: {stats['total_conversions']:6d}")
print(f" 转化率: {stats['conversion_rate']:.4f}")
print(f"{'-'*30}")
time.sleep(interval_seconds)
print(f"\n{'='*60}")
print("监控结束 - 最终统计结果:")
print(f"{'='*60}")
final_summary = self.get_summary()
for variant, stats in final_summary.items():
print(f"实验组 {variant}: {stats['conversion_rate']:.4f}")
return final_summary
# 模拟数据收集
def simulate_ab_test_experiment():
"""模拟A/B测试实验"""
collector = ABTestDataCollector(
experiment_id="button_color_202405",
variant_a_name="蓝色按钮",
variant_b_name="红色按钮"
)
# 模拟1000个用户
num_users = 1000
# 模拟对照组(蓝色按钮)转化率10%
# 模拟实验组(红色按钮)转化率12%
conversion_rates = {
"蓝色按钮": 0.10,
"红色按钮": 0.12
}
for user_id in range(num_users):
# 分配实验组
variant = assign_to_group(user_id, groups=["蓝色按钮", "红色按钮"])
# 模拟会话开始
collector.log_event(user_id, variant, 'session_start')
# 模拟转化事件(根据转化率随机生成)
if random.random() < conversion_rates[variant]:
collector.log_event(user_id, variant, 'conversion')
return collector
# 运行模拟实验
collector = simulate_ab_test_experiment()
summary = collector.get_summary()
print("A/B测试模拟结果摘要:")
for variant, stats in summary.items():
print(f"\n{variant}:")
print(f" 独立用户数: {stats['unique_users']}")
print(f" 总会话数: {stats['total_sessions']}")
print(f" 总转化数: {stats['total_conversions']}")
print(f" 转化率: {stats['conversion_rate']:.4f}")2.2.5 第五步:统计分析与结果解读
2.2.5.1 假设检验
A/B测试通常使用双比例Z检验或卡方检验来比较两组的转化率差异。
python
import numpy as np
from scipy import stats
def analyze_ab_test_results(control_conversions, control_samples,
treatment_conversions, treatment_samples,
alpha=0.05):
"""
分析A/B测试结果
参数:
control_conversions: 对照组转化数
control_samples: 对照组样本数
treatment_conversions: 实验组转化数
treatment_samples: 实验组样本数
alpha: 显著性水平
返回:
分析结果字典
"""
# 计算转化率
p_control = control_conversions / control_samples
p_treatment = treatment_conversions / treatment_samples
# 计算合并比例
p_pool = (control_conversions + treatment_conversions) / (control_samples + treatment_samples)
# 计算标准误差
se = np.sqrt(p_pool * (1 - p_pool) * (1/control_samples + 1/treatment_samples))
# 计算Z统计量
z_score = (p_treatment - p_control) / se
# 计算p值(双尾检验)
p_value = 2 * (1 - stats.norm.cdf(abs(z_score)))
# 计算置信区间
margin_of_error = stats.norm.ppf(1 - alpha/2) * se
ci_lower = (p_treatment - p_control) - margin_of_error
ci_upper = (p_treatment - p_control) + margin_of_error
# 计算相对提升
relative_improvement = (p_treatment - p_control) / p_control * 100
# 计算统计功效(事后分析)
effect_size = abs(p_treatment - p_control)
power = stats.norm.cdf(z_score - stats.norm.ppf(1 - alpha/2)) + stats.norm.cdf(-z_score - stats.norm.ppf(1 - alpha/2))
# 做出决策
significant = p_value < alpha
decision = "拒绝原假设,实验组显著优于对照组" if significant and p_treatment > p_control else \
"拒绝原假设,对照组显著优于实验组" if significant and p_treatment < p_control else \
"无法拒绝原假设,两组无显著差异"
return {
'control_rate': p_control,
'treatment_rate': p_treatment,
'absolute_difference': p_treatment - p_control,
'relative_improvement': relative_improvement,
'z_score': z_score,
'p_value': p_value,
'confidence_interval': (ci_lower, ci_upper),
'significant': significant,
'statistical_power': power,
'decision': decision
}
def perform_comprehensive_ab_analysis(control_data, treatment_data):
"""执行全面的A/B测试分析"""
# 基本统计检验
results = analyze_ab_test_results(
control_data['conversions'], control_data['samples'],
treatment_data['conversions'], treatment_data['samples']
)
# 计算所需最小可检测效应(MDE)
def calculate_mde(alpha=0.05, power=0.8, baseline_rate=0.1, sample_size=5000):
"""计算最小可检测效应"""
from statsmodels.stats.proportion import proportion_effectsize
from statsmodels.stats.power import NormalIndPower
effect_size = NormalIndPower().solve_power(
effect_size=None,
nobs1=sample_size,
alpha=alpha,
power=power,
ratio=1
)
# 将效应量转换为百分比
z_alpha = stats.norm.ppf(1 - alpha/2)
z_beta = stats.norm.ppf(power)
mde = (z_alpha + z_beta) * np.sqrt(
baseline_rate * (1 - baseline_rate) * (2/sample_size)
)
return mde * 100 # 返回百分比
# 计算MDE
baseline_rate = control_data['conversions'] / control_data['samples']
mde = calculate_mde(baseline_rate=baseline_rate, sample_size=control_data['samples'])
results['minimum_detectable_effect'] = mde
# 贝叶斯分析(可选)
def bayesian_analysis(control_conversions, control_samples,
treatment_conversions, treatment_samples):
"""贝叶斯A/B测试分析"""
from scipy.stats import beta
# 使用Beta先验分布
alpha_prior = 1
beta_prior = 1
# 计算后验分布
posterior_control = beta(alpha_prior + control_conversions,
beta_prior + control_samples - control_conversions)
posterior_treatment = beta(alpha_prior + treatment_conversions,
beta_prior + treatment_samples - treatment_conversions)
# 计算实验组优于对照组的概率
samples = 100000
treatment_samples = posterior_treatment.rvs(samples)
control_samples = posterior_control.rvs(samples)
probability_better = np.mean(treatment_samples > control_samples)
# 计算期望损失
expected_loss = np.maximum(0, control_samples - treatment_samples).mean()
return {
'probability_treatment_better': probability_better,
'expected_loss_if_wrong': expected_loss
}
bayesian_results = bayesian_analysis(
control_data['conversions'], control_data['samples'],
treatment_data['conversions'], treatment_data['samples']
)
results.update(bayesian_results)
return results
# 示例数据分析
control_data = {
'conversions': 120,
'samples': 1200,
'revenue': 15000
}
treatment_data = {
'conversions': 145,
'samples': 1200,
'revenue': 18000
}
results = perform_comprehensive_ab_analysis(control_data, treatment_data)
print("A/B测试统计分析结果:")
print("=" * 60)
print(f"对照组转化率: {results['control_rate']:.4f} ({control_data['conversions']}/{control_data['samples']})")
print(f"实验组转化率: {results['treatment_rate']:.4f} ({treatment_data['conversions']}/{treatment_data['samples']})")
print(f"绝对差异: {results['absolute_difference']:.4f}")
print(f"相对提升: {results['relative_improvement']:.2f}%")
print(f"Z分数: {results['z_score']:.4f}")
print(f"P值: {results['p_value']:.6f}")
print(f"95%置信区间: [{results['confidence_interval'][0]:.4f}, {results['confidence_interval'][1]:.4f}]")
print(f"是否显著: {'是' if results['significant'] else '否'}")
print(f"统计功效: {results['statistical_power']:.4f}")
print(f"最小可检测效应(MDE): {results['minimum_detectable_effect']:.2f}%")
print(f"实验组更好的概率(贝叶斯): {results['probability_treatment_better']:.4f}")
print(f"决策: {results['decision']}")
print("=" * 60)2.2.5.2 数据可视化
python
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
def visualize_ab_test_results(results_dict, control_data, treatment_data):
"""可视化A/B测试结果"""
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
fig.suptitle('A/B测试结果综合分析报告', fontsize=16, fontweight='bold', y=1.02)
# 1. 转化率对比条形图
ax1 = axes[0, 0]
rates = [results_dict['control_rate'], results_dict['treatment_rate']]
groups = ['对照组', '实验组']
colors = ['#3498db', '#e74c3c']
bars = ax1.bar(groups, rates, color=colors, alpha=0.8)
ax1.set_title('转化率对比', fontsize=14, pad=12)
ax1.set_ylabel('转化率', fontsize=12)
ax1.set_ylim(0, max(rates) * 1.2)
# 在条形上添加数值标签
for bar, rate in zip(bars, rates):
height = bar.get_height()
ax1.text(bar.get_x() + bar.get_width()/2., height + 0.001,
f'{rate:.4f}', ha='center', va='bottom', fontsize=11)
# 添加提升百分比标注
improvement = results_dict['relative_improvement']
ax1.text(0.5, max(rates) * 1.1, f'相对提升: {improvement:.1f}%',
ha='center', va='bottom', fontsize=12,
bbox=dict(boxstyle="round,pad=0.3", facecolor="yellow", alpha=0.7))
# 2. 置信区间图
ax2 = axes[0, 1]
diff = results_dict['absolute_difference']
ci_lower, ci_upper = results_dict['confidence_interval']
ax2.errorbar([0], [diff], yerr=[[abs(diff - ci_lower)], [abs(ci_upper - diff)]],
fmt='o', capsize=10, capthick=2, markersize=10,
color='#2c3e50', ecolor='#7f8c8d')
ax2.axhline(y=0, color='red', linestyle='--', alpha=0.5, label='无差异线')
ax2.set_xlim(-0.5, 0.5)
ax2.set_xticks([])
ax2.set_title('效应量估计与95%置信区间', fontsize=14, pad=12)
ax2.set_ylabel('转化率差异', fontsize=12)
ax2.legend()
# 标注置信区间
ax2.text(0.2, diff, f'{diff:.4f}', va='center', fontsize=11)
ax2.text(0.2, ci_lower, f'下限: {ci_lower:.4f}', va='center', fontsize=10)
ax2.text(0.2, ci_upper, f'上限: {ci_upper:.4f}', va='center', fontsize=10)
# 3. P值分布与显著性
ax3 = axes[0, 2]
p_value = results_dict['p_value']
alpha = 0.05
# 模拟P值分布
np.random.seed(42)
simulated_p_values = np.random.beta(1, 20, 1000) # 大部分小值
ax3.hist(simulated_p_values, bins=30, alpha=0.7, color='#3498db', edgecolor='black')
ax3.axvline(x=p_value, color='red', linewidth=3, label=f'观测P值: {p_value:.6f}')
ax3.axvline(x=alpha, color='orange', linewidth=2, linestyle='--', label=f'显著性水平: {alpha}')
# 着色显著性区域
ax3.axvspan(0, alpha, alpha=0.2, color='green', label='显著区域')
ax3.set_title('P值分布与显著性检验', fontsize=14, pad=12)
ax3.set_xlabel('P值', fontsize=12)
ax3.set_ylabel('频率', fontsize=12)
ax3.legend()
# 4. 统计功效分析
ax4 = axes[1, 0]
# 计算不同样本量下的统计功效
sample_sizes = np.arange(100, 5000, 100)
powers = []
baseline_rate = control_data['conversions'] / control_data['samples']
effect_size = results_dict['absolute_difference']
for n in sample_sizes:
z_alpha = stats.norm.ppf(1 - alpha/2)
z_power = effect_size / np.sqrt(baseline_rate * (1 - baseline_rate) * (2/n))
power = stats.norm.cdf(z_power - z_alpha) + stats.norm.cdf(-z_power - z_alpha)
powers.append(power)
ax4.plot(sample_sizes, powers, linewidth=2.5, color='#9b59b6')
ax4.axhline(y=0.8, color='red', linestyle='--', alpha=0.7, label='目标功效 (0.8)')
ax4.axvline(x=control_data['samples'], color='green', linestyle='--',
alpha=0.7, label=f'实际样本量 ({control_data["samples"]})')
ax4.set_title('样本量与统计功效关系', fontsize=14, pad=12)
ax4.set_xlabel('每组样本量', fontsize=12)
ax4.set_ylabel('统计功效', fontsize=12)
ax4.legend()
ax4.grid(True, alpha=0.3)
# 5. 贝叶斯分析可视化
ax5 = axes[1, 1]
# 生成Beta分布
from scipy.stats import beta
alpha_prior = 1
beta_prior = 1
posterior_control = beta(alpha_prior + control_data['conversions'],
beta_prior + control_data['samples'] - control_data['conversions'])
posterior_treatment = beta(alpha_prior + treatment_data['conversions'],
beta_prior + treatment_data['samples'] - treatment_data['conversions'])
x = np.linspace(0, 0.2, 1000)
ax5.plot(x, posterior_control.pdf(x), label='对照组后验分布', linewidth=2.5, color='#3498db')
ax5.plot(x, posterior_treatment.pdf(x), label='实验组后验分布', linewidth=2.5, color='#e74c3c')
# 填充实验组更好的区域
ax5.fill_between(x, posterior_treatment.pdf(x),
where=(posterior_treatment.pdf(x) > posterior_control.pdf(x)),
alpha=0.3, color='#e74c3c', label='实验组更好区域')
ax5.set_title('贝叶斯后验分布分析', fontsize=14, pad=12)
ax5.set_xlabel('转化率', fontsize=12)
ax5.set_ylabel('概率密度', fontsize=12)
ax5.legend()
ax5.grid(True, alpha=0.3)
# 6. 决策矩阵
ax6 = axes[1, 2]
ax6.axis('off')
# 创建决策矩阵文本
decision_text = f"""
A/B测试决策报告
{'='*40}
实验信息:
- 对照组样本量:{control_data['samples']}
- 实验组样本量:{treatment_data['samples']}
- 测试时长:7天
统计结果:
- 转化率差异:{results_dict['absolute_difference']:.4f}
- 相对提升:{results_dict['relative_improvement']:.2f}%
- P值:{results_dict['p_value']:.6f}
- 统计显著性:{'是' if results_dict['significant'] else '否'}
贝叶斯分析:
- 实验组更好的概率:{results_dict['probability_treatment_better']:.4f}
- 错误决策的期望损失:{results_dict['expected_loss_if_wrong']:.6f}
业务影响:
- 对照组收入:¥{control_data['revenue']}
- 实验组收入:¥{treatment_data['revenue']}
- 收入提升:{(treatment_data['revenue']/control_data['revenue']-1)*100:.1f}%
最终决策:{results_dict['decision']}
"""
# 根据显著性设置颜色
if results_dict['significant'] and results_dict['treatment_rate'] > results_dict['control_rate']:
box_color = 'lightgreen'
decision_color = 'darkgreen'
elif results_dict['significant']:
box_color = 'lightcoral'
decision_color = 'darkred'
else:
box_color = 'lightyellow'
decision_color = 'darkorange'
ax6.text(0.1, 0.95, decision_text, transform=ax6.transAxes,
fontsize=10, family='monospace', verticalalignment='top',
bbox=dict(boxstyle="round,pad=1", facecolor=box_color, edgecolor=decision_color, linewidth=2))
ax6.set_title('决策建议矩阵', fontsize=14, pad=12, color=decision_color)
plt.tight_layout()
plt.show()
return fig
# 生成可视化报告
fig = visualize_ab_test_results(results, control_data, treatment_data)2.3 A/B测试的最佳实践与常见陷阱
2.3.1 最佳实践
- 明确目标:每次测试只解决一个问题
- 一次只改变一个变量:便于归因
- 确保样本量充足:避免统计功效不足
- 运行足够长时间:覆盖用户周期和不同时间段
- 监控护栏指标:确保不会损害用户体验
- 记录完整的实验文档:便于复现和分析
- 建立实验文化:鼓励团队提出假设并验证
2.3.2 常见陷阱及避免方法
| 陷阱 | 表现 | 避免方法 |
|---|---|---|
| 过早停止测试 | 看到初步显著结果就停止 | 预先确定样本量,使用序贯分析 |
| 多重比较问题 | 同时测试多个指标,增加假阳性 | 使用Bonferroni校正,控制族错误率 |
| 新奇效应 | 用户对新功能好奇导致短期行为改变 | 延长测试时间,观察长期趋势 |
| 选择偏差 | 用户分组不随机 | 使用稳定的哈希函数进行分流 |
| 样本比例失衡 | 实验组与对照组样本量差异大 | 定期检查分流均匀性,及时调整 |
| 忽略季节性 | 测试期间遇到节假日等特殊时期 | 避开特殊时期,或使用同期群对比 |
| 过度解读微小差异 | 统计显著但业务意义不大的差异 | 结合最小重要差异(MID)进行决策 |
3、总结
A/B测试是数据驱动决策的核心工具,它通过科学的方法帮助我们在不确定性的世界中做出更明智的选择。掌握A/B测试不仅需要理解统计原理,还需要结合业务实际,避免常见陷阱。
关键要点回顾:
- 明确假设:清晰的假设是成功测试的基础
- 正确设计:合理的实验设计确保结果可靠
- 充分样本:足够的样本量保证统计功效
- 全面分析:结合频率学派和贝叶斯方法进行分析
- 谨慎决策:统计显著不等于业务重要
- 持续学习:每次测试都是学习机会
我是小鱼:
- CSDN 博客专家;
- AIGC MVP专家;
- 阿里云 专家博主;
- 企业认证金牌面试官;
- 多名企签约作者、认证讲师、特邀讲师等;
- 名企签约职场面试培训、职场规划师;
- 多个国内主流技术社区的认证专家博主;
- 多款主流产品(阿里云等)评测一等奖获得者;
关注小鱼,学习【数据分析】最新最全的领域知识。