1. 排序相关概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
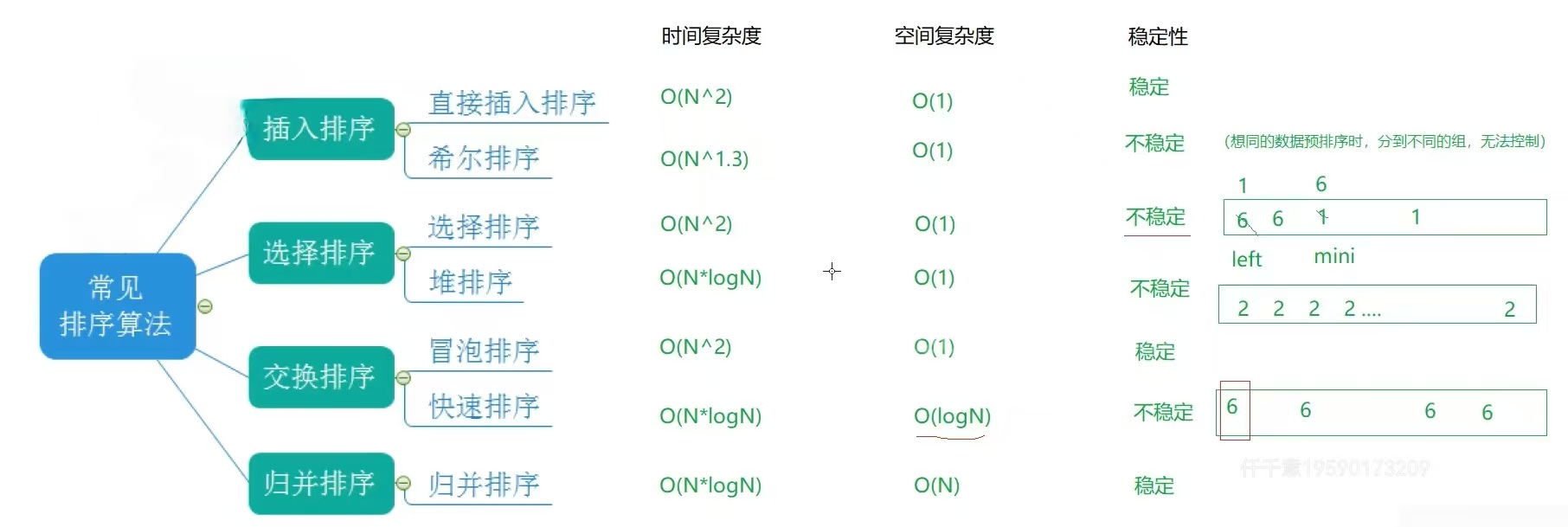
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排 序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不断地在内外存之间移动数据的排序。
注:以下所有排序算法皆以升序来介绍
2. 冒泡排序
冒泡排序作为最早接触的排序算法,其排序核心是相邻两数比较,大的向后换,达到将最大值"浮"到最末端的效果,然后剔除最大值后再遍历,"浮"出剩余数的最大值,直至有序。冒泡排序的运行效率非常低下,实际排序问题中用不到,只做排序学习入门之用。
以下是代码示例:
cpp
void BubbleSort(int* a, int n)
{
for (int j = 0; j < n; j++)
{
//falg判断当前数组是否有序 是?跳出循环 否?继续冒泡
int falg = 0;
for (int i = 0; i < n - 1 - j; i++)
{
if (a[i] > a[i + 1])
{
Swap(&a[i], &a[i + 1]);
falg = 1;
}
}
if (falg == 0)
break;
}
}3. 插入排序
3.1 直接插入排序
直接插入排序核心思想是数组第一个元素是有序的,第二个元素与第一个元素比较,如果小于第一个元素,就向前调整;前两个有序,第三个元素与前面已有序元素比较,插入到合适位置,遍历至末尾元素,数组有序。
以下是代码示例:
cpp
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
//单次排序
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + 1] = a[end];
--end;
}
else
{
break;
}
}
//跳出循环 将tmp变量插入
a[end + 1] = tmp;
}
}3.2 希尔排序
3.2.1 希尔排序原理
希尔排序是对直接插入排序的一个优化,直接插入排序在排列较有序数组时存在致命的缺陷。比如要将一个降序数据串排为升序时,每一次比较都要交换数据,这时相邻元素两两比较的原则让大数据元素缓慢的向后交换,小数据元素缓慢的向前交换让此算法的效率变得和冒泡排序一样,那么有没有办法可以让大数据元素尽可能快的向后换呢?希尔排序就实现了这样的效果,可以在这种情况下,依然抗打。
希尔排序核心思想依然是插入排序,但在插入排序之前,会对数据先进行多次预排序。预排序思想:把所有数据分为gap组,每隔gap个元素的数据作为一组,每个组内先进行插入排序,让较大元素放到后面,改变gap值,多次预排序,此时数组已经处于基本有序的情况了,再进行插入排序,到达目的。
3.2.2 代码示例
关于gap值如何取,代码中gap = gap / 3 + 1,是大量实验数据证明,gap / 3在效率上比gap / 2更优,因为gap / 2中存在公因子(比如4和2),会让已经预排序过的数据再次预排序,效率受限,而gap / 3 + 1避免了公因子影响。
cpp
void ShellSort(int* a, int n)
{
int gap = n;
//多次预排序 让数据更接近有序
while (gap > 1)
{
// +1是保证最后一次gap值为1
gap = gap / 3 + 1;
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (tmp < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}4. 选择排序
4.1 选择排序
选择排序核心思想是遍历数组,选出最大值和最小值放到起始和末尾,剩余数据再遍历,选出次大的数据放到合适位置,直至有序。
代码示例:
cpp
void SelectSort(int* a, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
int min = begin, max = begin;
for (int i = begin + 1; i <= end; i++)
{
if (a[i] < a[min])
{
min = i;
}
if (a[i] > a[max])
{
max = i;
}
}
Swap(&a[begin], &a[min]);
if (max == begin)
max = min;
Swap(&a[end], &a[max]);
++begin;
--end;
}
}4.2 堆排序
堆排序在上文二叉树篇中已有详细介绍,在这不做介绍
5. 快速排序
5.1 快速排序原理
快速排序最早是英国一位计算机科学家托尼·霍尔提出,将排序效率提升到当时的顶尖效率,其原理时:将数组最左或最右为基准值(这里以最左为例),从数组末尾开始向左查找,直到找到比基准值小的值;然后从数组第二个元素开始,向右查找比基准值大的值,交换两数,然后重复上述操作,右找小,左找大,交换,直至左右相遇,相遇位置就是基准值的最终位置,然后递归左半部分和右半部分,重复交换,确定基准值位置,直到递归到数据为1或空,此时数组即有序,开始返回。
可能有人会有疑问:**与基准值交换的数据不会比基准值大吗?**答案是对,一定。原因不难分析,左右相遇有两种情况,要么右遇左,要么左遇右,如果是右遇左,相遇位置是上次左停的位置(左边停下来的位置的数据是上次与右边交换后的比基准值小的数据);如果是左遇右·,相遇位置是右边停下的位置(右边停下来一定是找到了比基准值小的数据),由此可知,右边先找也是定死的,否则相遇位置就是比基准值大的数据了。
5.2 hoare版本
5.2.1 快速排序效率优化
上面的快速排序仍存在缺陷,当基准值取值过于极端时,会导致查找时一直找不到比基准值小的值,导致效率下降。对于基准值取值问题,我们这里采用取左、中、右三个元素取中间值做基准值的方法,保证基准值一定不是最大值。当然,快速排序人如其名,它的效率还可以提升,快速排序内部递归深度越深,分割的区间就越多,要遍历的数据就越少,而使用快速排序的目的是在面对庞大数据量时可以让数据串更快的接近有序,小区间再使用快排,不亚于大炮打蚊子,有栈溢出风险,还会降低排序效率,所有我们可以给一个限定,当递归分割出来的左右数据总数小于10个的时候,我们使用插入排序,不再向下递归。
5.2.2 代码示例
cpp
int GetMid(int* a, int left, int right)
{
int mid = (left + right) / 2;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
return mid;
else if (a[left] < a[right])
return right;
else
return left;
}
else
{
if (a[mid] > a[right])
return mid;
else if (a[left] > a[right])
return right;
else
return left;
}
}
void PartSort1(int* a, int left, int right)
{
if (left >= right)
return;
//小区间优化
if (right - left + 1 < 10)
{
InsertSort(a + left, right - left + 1);
return;
}
else
{
//三数取中作基准数 防止较顺序数组导致效率降低
int mid = GetMid(a, left, right);
Swap(&a[mid], &a[left]);
int keyi = left;
int begin = left, end = right;
while (begin < end)
{
//内部限定begin < end保证左右相遇一定停下来
while (begin < end && a[end] >= a[keyi])
{
--end;
}
while (begin < end && a[begin] <= a[keyi])
{
++begin;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[begin], &a[keyi]);
keyi = begin;
PartSort1(a, left, keyi - 1);
PartSort1(a, keyi + 1, right);
}
}有人觉得hoare版的快速排序限定条件多,且不好理解(作者初学时也感觉好难理解呀,霍尔这个人是天才吧),所以有人基于霍尔排序的思想,想出了挖坑法和前后指针法,这两种方法在效率上没有任何的提升,且同样需要三数取中和小区间优化,他们只是简化了逻辑,更易于理解。
5.3 挖坑法
挖坑法是把基准值拿出来,基准值所处位置当作坑位,右边找到比基准值小的数据后,甩到坑里,右边形成新的坑,左边找到比基准值大的数据甩到右边的新坑中,直至相遇后,把基准值放到坑里,然后同样递归左右区间,直至有序。
代码示例:
cpp
void PartSort2(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = left, pit = left;
int begin = left, end = right;
while (begin < end)
{
while (begin < end && a[end] < a[keyi])
{
--end;
}
a[pit] = a[end];
pit = end;
while (begin < end && a[begin] > a[keyi])
{
++begin;
}
a[pit] = a[begin];
pit = begin;
}
a[pit] = a[keyi];
PartSort2(a, left, pit - 1);
PartSort2(a, pit + 1, right);
}5.4 前后指针法
前后指针法是使用两个指针(prev、cur)来完成交换,prev指向基准值,cur指向基准值的下一个位置,cur指向的位置如果小于基准值,且prev与cur之间没有元素,就让cur++向后找,同时prev++;如果prev与cur之间有元素(比基准值大),此时让prev++再与cur交换。如果cur指向的位置大于基准值,则cur++向后找,cur遍历到末尾后,cur玉prev之间的元素都比基准值大,此时prev的位置与基准值交换,完成一次,再递归左右区间,直至有序。
代码示例:
cpp
void PartSort3(int* a, int left, int right)
{
if (left >= right)
return;
int keyi = left;
int prev = left, cur = left + 1;
while (cur <= right)
{
if (a[cur] < a[keyi] && ++prev != cur)
{
Swap(&a[cur], &a[prev]);
}
++cur;
}
Swap(&a[prev], &a[keyi]);
keyi = prev;
PartSort3(a, left, keyi - 1);
PartSort3(a, keyi + 1, right);
}5.5 快速排序非递归实现
5.5.1 代码思考
快速排序排序很高效,但其依靠递归实现的根本,在面对庞大数据量时,难保不会有栈溢出的风险,所以就需要非递归(循环)版本来解决这个不可控的问题。实现非递归就需要知道每一次递归的改变的因素,我们手动实现这些因素的控制,循环多次单次调整的函数,就能减少栈区的额外消耗。
写过递归版本后,我们知道每一次递归,函数的左右边界都会改变,我们可以依靠数据结构中的栈来记录左右边界的变化:开始的时候,把数组的起始末尾位置入栈,取栈中数据作为作为单次调整的左右边界,然后分别判断左右边界与基准值之间有没有元素,如果有,把左右区间入栈,再分别进行调整;如果没有,说明左(右)区间只有一个元素,已经有序,不再入栈,所以循环结束条件就是栈为不为空。
5.5.2 代码示例
栈的实现在之前的博客中有过讲述,此处不再处理。
cpp
//(非递归快排单次调整函数)
int QuickSortOnce(int* a, int left, int right)
{
int keyi = left;
int begin = left, end = right;
while (begin < end)
{
while (begin < end && a[end] >a[keyi])
{
--end;
}
while (begin < end && a[begin] < a[keyi])
{
++begin;
}
Swap(&a[begin], &a[end]);
}
Swap(&a[keyi], &a[begin]);
keyi = begin;
return keyi;
}
#include "Stack.h"
// 快速排序 非递归实现
void QuickSortNonR(int* a, int left, int right)
{
ST st;
STInit(&st);
STPush(&st, right);
STPush(&st, left);
while (!STEmpty(&st))
{
int begin = STTop(&st);
STPop(&st);
int end = STTop(&st);
STPop(&st);
int keyi = QuickSortOnce(a, begin, end);
if (begin < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st, begin);
}
if (end > keyi + 1)
{
STPush(&st, end);
STPush(&st, keyi + 1);
}
}
STDestory(&st);
}6. 归并排序
6.1 归并排序递归实现
6.1.1 归并排序原理
归并排序核心思想源于两个有序数组的合并(新数组依然保持有序):动态开辟一个新数组,定义两个指针分别指向两个数组的头,判断两数大小,小的放到新数组中,然后++,再比较,小的放到新数组,直到有一个遍历到末尾,此时把另一个数组的剩余元素循环入新数组,即有序。
归并排序就是依靠这个逻辑来实现,但数组中元素是无序的,那要怎么办?聪明的你不难想到,那我先递归分割数据直到变成一个个单数据区间呗,单个数据的比较肯定是可行的,排完单个数据返回上一层后,两个数据的比较也是有序的了,返回到最外层时,也就是左右区间(有序数组)的排序了
6.1.2 代码示例
使用子函数是为了避免改变参数个数。区间划分只能是begin到mid,mid+1到end,而不能是begin到mid-1,mid到end或者begin到mid,mid到end(会因为mid计算和划分逻辑冲突而出现死循环的情况),还要注意:向新数组拷贝数据时,memcpy要传入正确的起始位置和数据个数,否则会导致数据覆盖,影响结果。
cpp
//(递归归并排序内部函数)
void _MergeSort(int* a, int* tmp, int begin, int end)
{
if (begin >= end)
return;
int mid = (begin + end) / 2;
_MergeSort(a, tmp, begin, mid);
_MergeSort(a, tmp, mid + 1, end);
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
//归并排序
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
if (tmp == NULL)
{
perror("MergeSort::malloc fail");
return;
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
tmp = NULL;
}6.2 归并排序非递归实现
6.2.1 代码思考
归并排序同快速排序一样,依靠递归实现总不是长久之计,所以我们依然需要实现非递归版本,递归版本每次改变因素是两组待比较数组的个数(从单个数据比较开始),非递归我们可以使用一个变量控制单次归并的数组的元素个数,直接从数组头开始遍历让数据两两比较,但需要注意越界的处理。
6.2.2 代码示例
越界情况:分为end1越界,begin2越界和end2越界三种情况,end1越界时,begin2一定越界,可以看作一种情况处理,这种情况属于没有另一组与其比较,而其自身本就有序,所以直接结束此次遍历即可;end2越界的情况,是第二组数据个数不够,所以要改变end2为数组末尾,再与第一组比较。
cpp
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(n * sizeof(int));
if (tmp == NULL)
{
perror("MergeSort::malloc fail");
return;
}
//gap表示当前归并的单组数据个数
int gap = 1;
while (gap < n)
{
int j = 0;//j控制tmp数组下标
//控制单次归并
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
//处理越界情况
if (begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}7. 计数排序
7.1 计数排序原理
计数排序是利用数组自身下标的有序性来实现排序的,先记录数据串中所有数据出现的次数到新数组的对应位置中,最小的数据出现的次数记录在数组第一个位置,依次向后,记录到最后一个数据后,开始排序,数组下标加上最小值就是数据本身的大小。注意:计数排序只适用于整数且数据密集的数据串排序。(时间复杂度为O(n + k)空间复杂度为O(k)k是数据范围)
7.2 代码示例
cpp
void CountSort(int* a, int n)
{
int min = a[0], max = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
int range = max - min + 1;
//计数
int* count = (int*)calloc(range, sizeof(int));
if (count == NULL)
{
perror("calloc fail");
return;
}
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
//排序
int j = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
a[j++] = i + min;
}
}
free(count);
}8. 各排序算法性能比较