贪心 - 后篇 - 技术栈

738. 单调递增的数字 - 力扣（LeetCode）

解法（贪心）：

a. 为了方便处理数中的每一位数字，可以先讲整数转换成字符串；
b. 从左往右扫描，找到第一个递减的位置；
c. 从这个位置向前推，推到相同区域的最左端；
d. 该点的值 -1，后面的所有数统一变成 9。

cpp 复制代码

class Solution {
public:
    int monotoneIncreasingDigits(int n) {
        string str = to_string(n);
        int i  = 0, m = str.size();
        while(i + 1 < m && str[i] <= str[i + 1]) ++i;
        if(i == m - 1) return n;
        while(i - 1 >= 0 && str[i] == str[i - 1]) i--;
        --str[i++];
        for(; i < m; ++i) str[i] = '9';
        return stoi(str);
    }
};

991. 坏了的计算器 - 力扣（LeetCode）

解法（贪心）：

贪心策略：正难则反

当 "反着" 来思考的时候，我们发现：

i. 当 end <= begin 的时候，只能执行「加法」操作；
ii. 当 end > begin 的时候，对于「奇数」来说，只能执行「加法」操作；对于「偶数」来说，最好的方式就是执行「除法」操作这样的话，每次的操作都是「固定唯一」的。

cpp 复制代码

class Solution {
public:
    int brokenCalc(int startValue, int target) {
        int ret = 0;
        while(target > startValue) {
            if(target % 2) ++target;
            else target /= 2;
            ++ret;
        }
        return ret + startValue - target;
    }
};

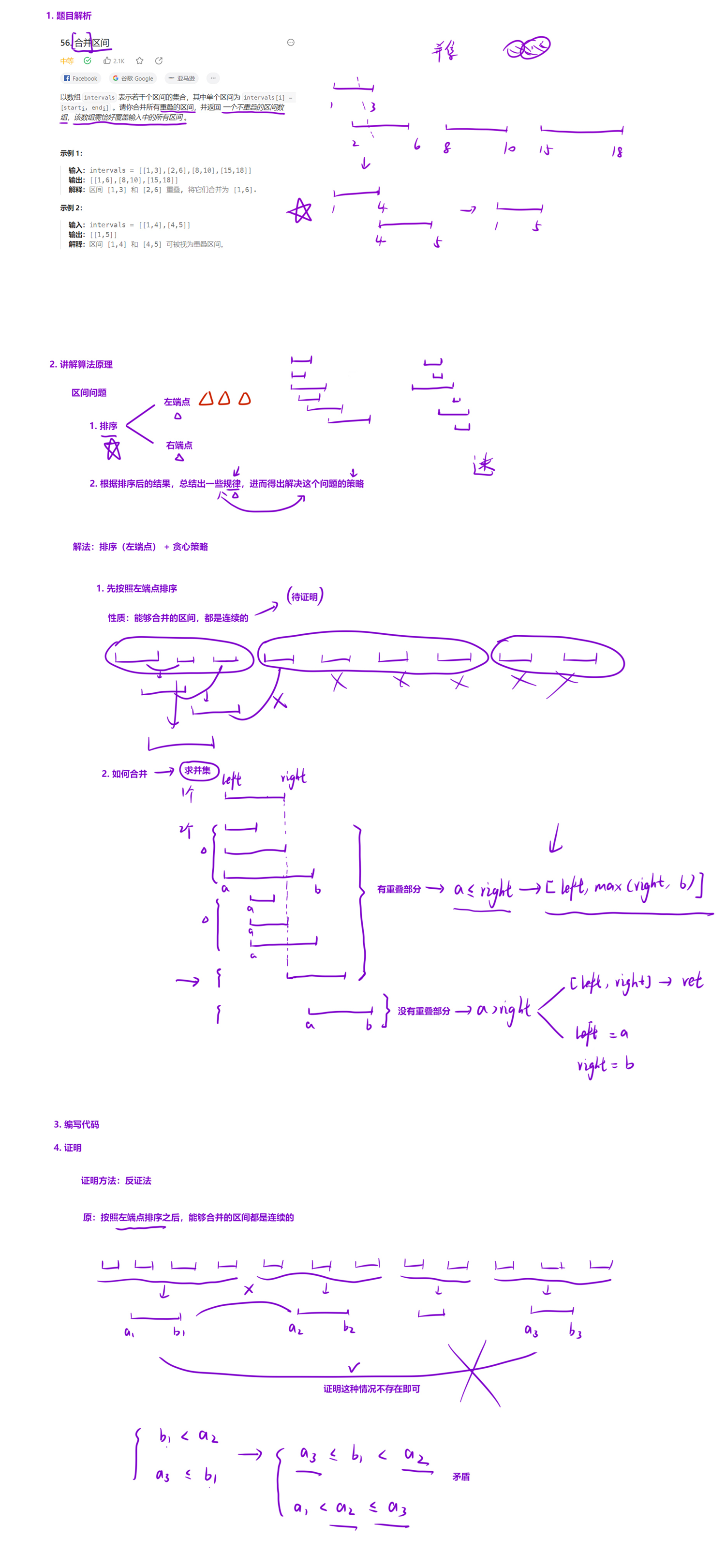
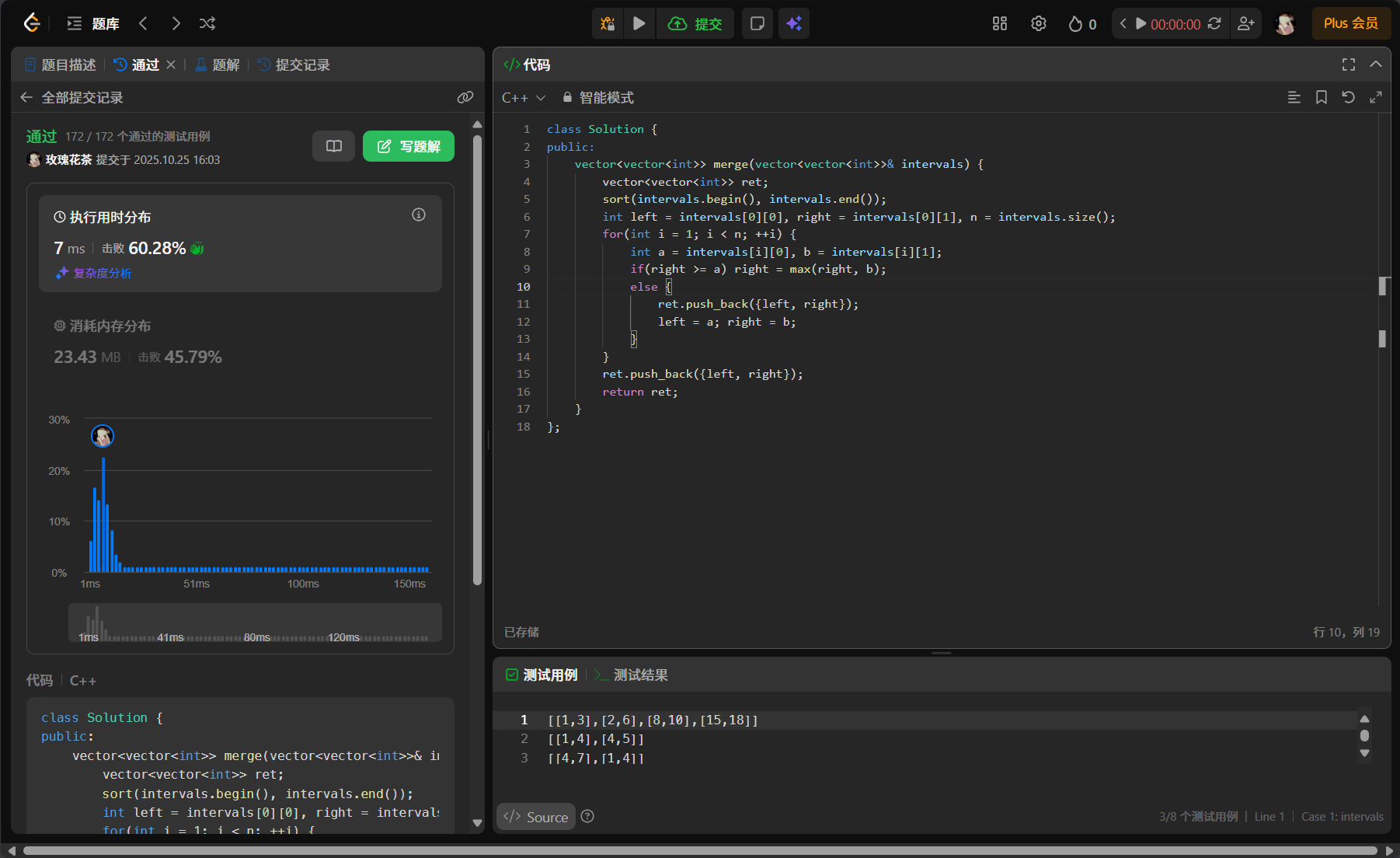
56. 合并区间 - 力扣（LeetCode）

解法（排序 + 贪心）：

贪心策略：

a. 先按照区间的「左端点」排序：此时我们会发现，能够合并的区间都是连续的；
b. 然后从左往后，按照求「并集」的方式，合并区间。

如何求并集：

由于区间已经按照「左端点」排过序了，因此当两个区间「合并」的时候，合并后的区间：

a. 左端点就是「前一个区间」的左端点；
b. 右端点就是两者「右端点的最大值」。

cpp 复制代码

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> ret;
        sort(intervals.begin(), intervals.end());
        int left = intervals[0][0], right = intervals[0][1], n = intervals.size();
        for(int i = 1; i < n; ++i) {
            int a = intervals[i][0], b = intervals[i][1];
            if(right >= a) right = max(right, b);
            else {
                ret.push_back({left, right});
                left = a; right = b;
            }
        }
        ret.push_back({left, right});
        return ret;
    }
};

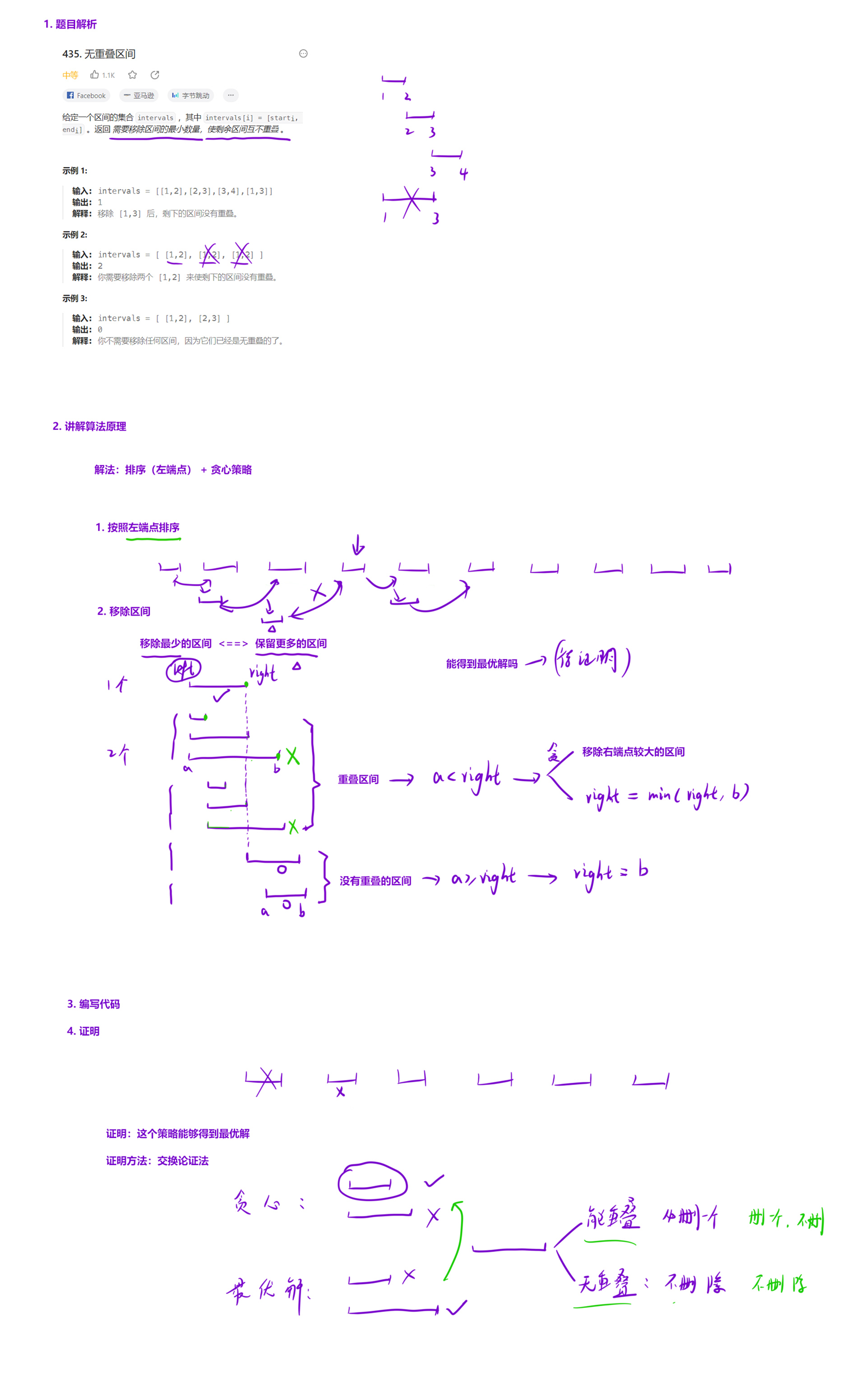
435. 无重叠区间 - 力扣（LeetCode）

解法（贪心）：

贪心策略：

a. 按照「左端点」排序；
b. 当两个区间「重叠」的时候，为了能够「在移除某个区间后，保留更多的区间」，我们应该把「区间范围较大」的区间移除。

如何移除区间范围较大的区间：

由于已经按照「左端点」排序了，因此两个区间重叠的时候，我们应该移除「右端点较大」的区间。

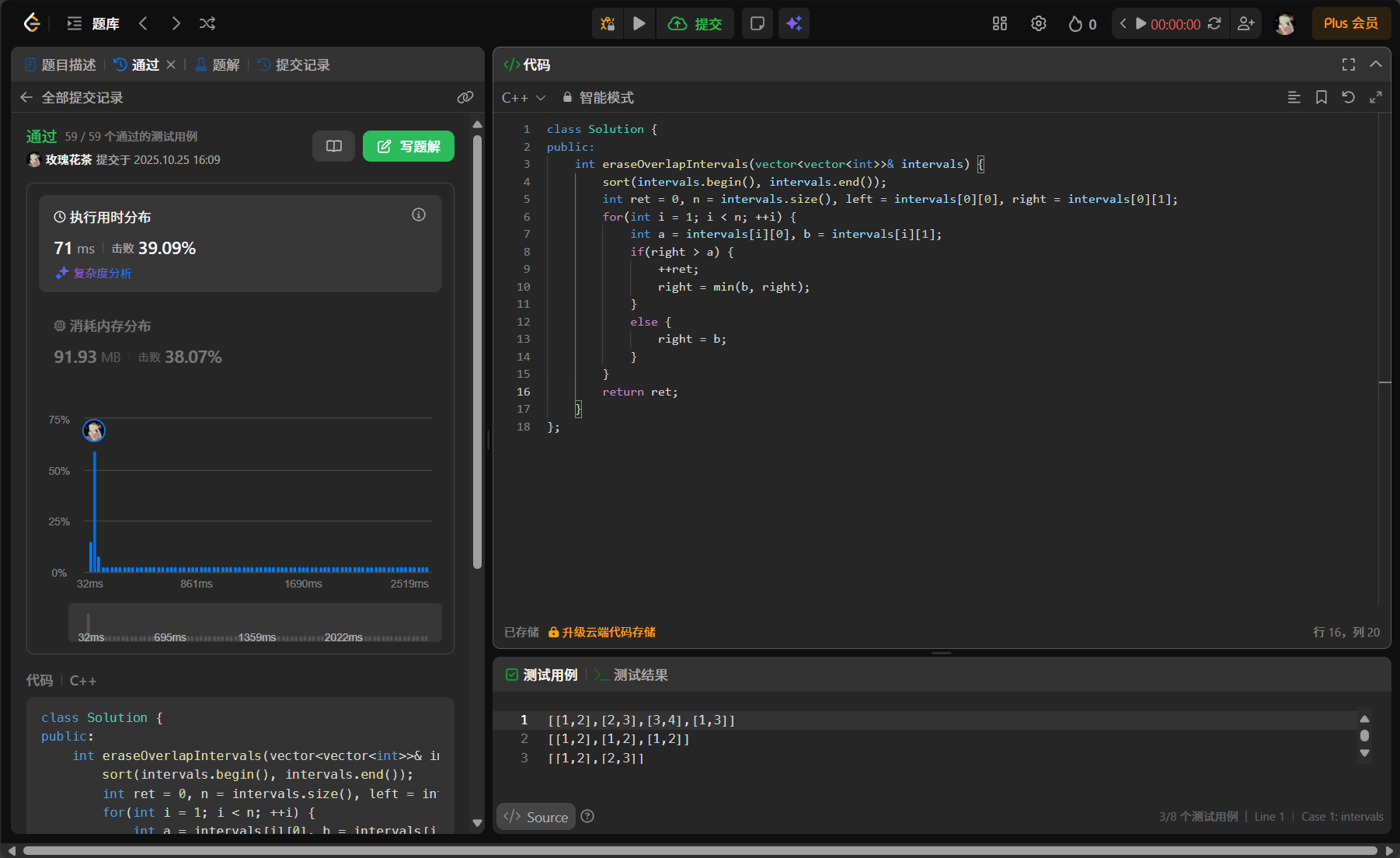
cpp 复制代码

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end());
        int ret = 0, n = intervals.size(), left = intervals[0][0], right = intervals[0][1];
        for(int i = 1; i < n; ++i) {
            int a = intervals[i][0], b = intervals[i][1];
            if(right > a) {
                ++ret;
                right = min(b, right);
            }
            else {
                right = b;
            }
        }
        return ret;
    }
};

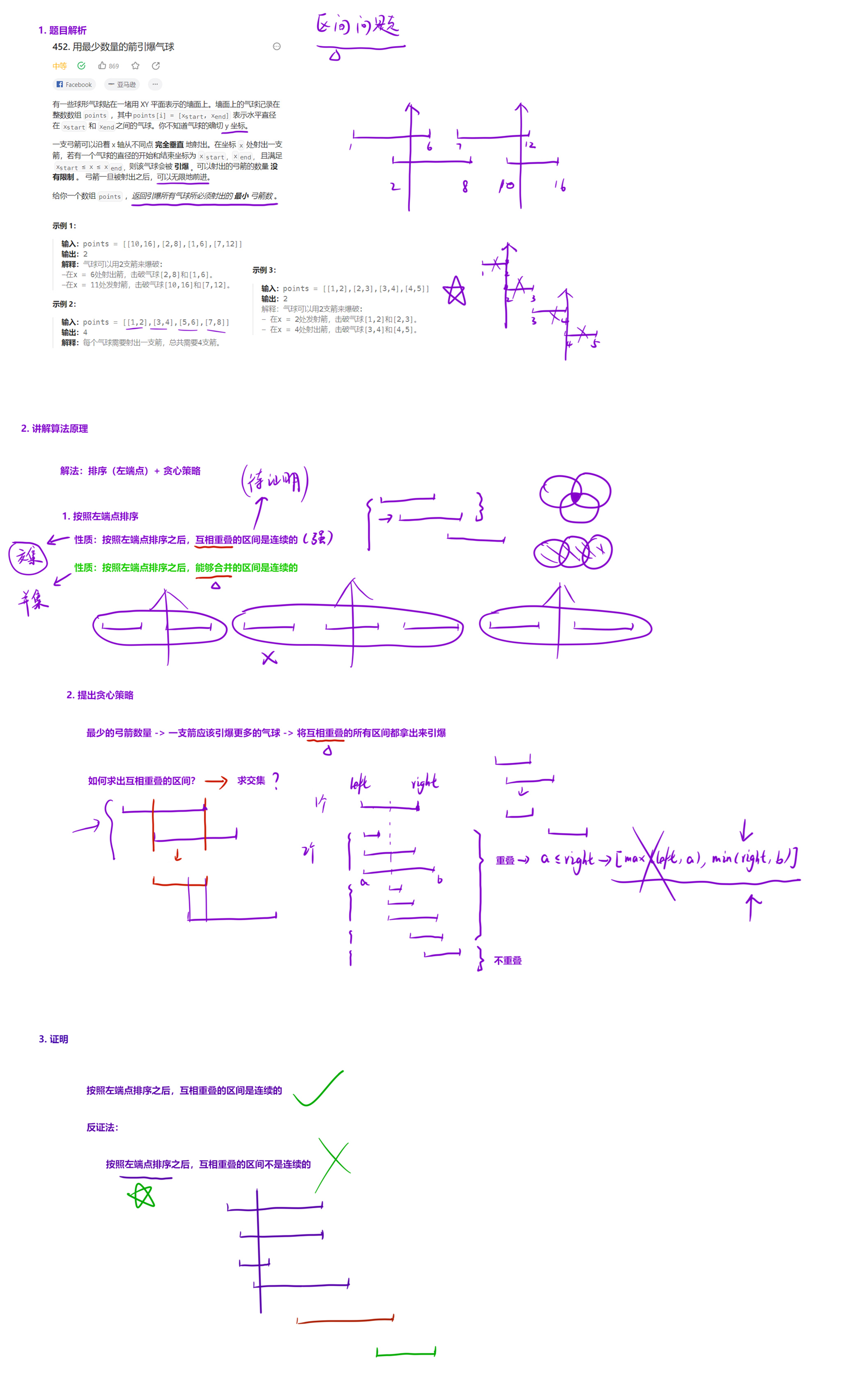
452. 用最少数量的箭引爆气球 - 力扣（LeetCode）

解法（贪心）：

贪心策略：

a. 按照左端点排序，我们发现，排序后有这样一个性质：「互相重叠的区间都是连续的」；
b. 这样，我们在射箭的时候，要发挥每一支箭「最大的作用」，应该把「互相重叠的区间」统一引爆。

如何求互相重叠区间？

由于我们是按照「左端点」排序的，因此对于两个区间，我们求的是它们的「交集」：

a. 左端点为两个区间左端点的「最大值」（但是左端点不会影响我们的合并结果，所以可以忽略）；
b. 右端点为两个区间右端点的「最小值」。

cpp 复制代码

class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        sort(points.begin(), points.end());
        int ret = 1, n = points.size(), right = points[0][1];
        for(int i = 1; i < n; ++i) {
            int a = points[i][0], b = points[i][1];
            if(right >= a) {
                right = min(right, b);
            }
            else {
                ++ret;
                right = b;
            }
        }
        return ret;
    }
};

397. 整数替换 - 力扣（LeetCode）

解法（贪心）：

贪心策略：

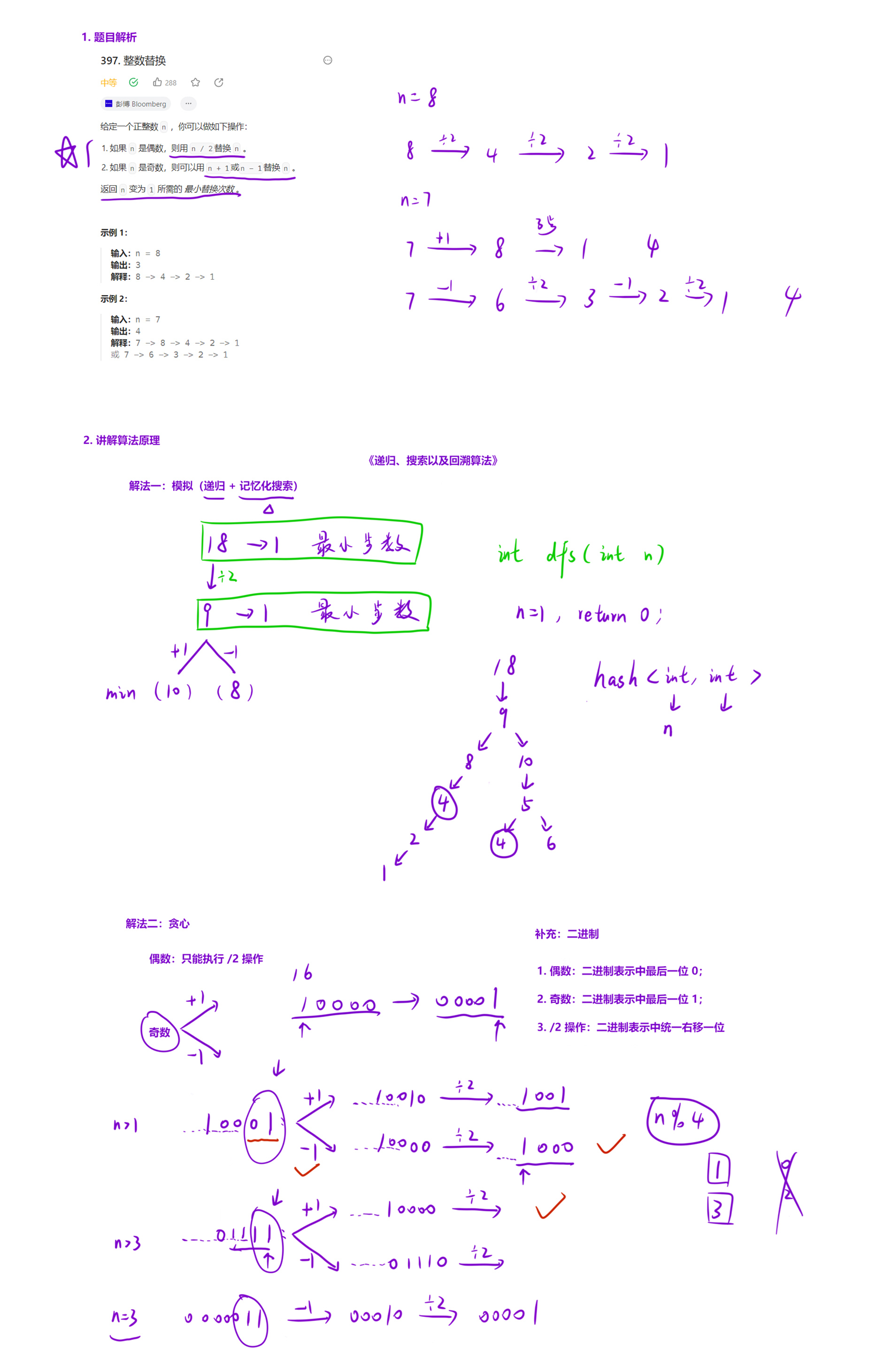
我们的任何选择，应该让这个数尽可能快的变成 1。

对于偶数：只能执行除 2 操作，没有什么分析的；

对于奇数：

ⅰ. 当 n==1 的时候，不用执行任何操作；
ⅱ. 当 n == 3 的时候，变成 1 的最优操作数是 2；
ⅲ. 当 n > 1 && n % 3 == 1 的时候，那么它的二进制表示是 ......01，最优的方式应该选择 -1，这样就可以把末尾的 1 干掉，接下来执行除法操作，能够更快的变成 1；
ⅳ. 当 n > 3 && n % 3 == 3 的时候，那么它的二进制表示是 ......11，此时最优的策略应该是 +1，这样可以把一堆连续的 1 转换成 0，更快的变成 1。

解法一：

cpp 复制代码

class Solution {
public:
    unordered_map<int, int> hash;
    int integerReplacement(int n) {
        return dfs(n);
    }

    int dfs(long long n) {
        if(hash.count(n)) return hash[n];
        if(n == 1) {
            hash[1] = 0;
            return 0;
        }
        if(n % 2 == 0) {
            hash[n] =  1 + dfs(n / 2);
            return hash[n];
        }
        else {
            hash[n] = 1  + min(dfs(n - 1), dfs(n + 1));
            return hash[n];
        }
    }
};

解法二：

cpp 复制代码

class Solution {
public:
    int integerReplacement(int n) {
        int ret = 0;
        while(n != 1) {
            if(n % 2 == 0) {
                n /= 2;
                ++ret;
            }
            else {
                if(n == 3) {
                    ret += 2;
                    n = 1;
                }
                else if(n % 4 == 1) {
                    n /= 2;
                    ret += 2;
                }
                else {
                    n = n / 2 + 1;
                    ret += 2;
                }
            }
        }
        return ret;
    }
};

354. 俄罗斯套娃信封问题 - 力扣（LeetCode）

解法一（动态规划）：

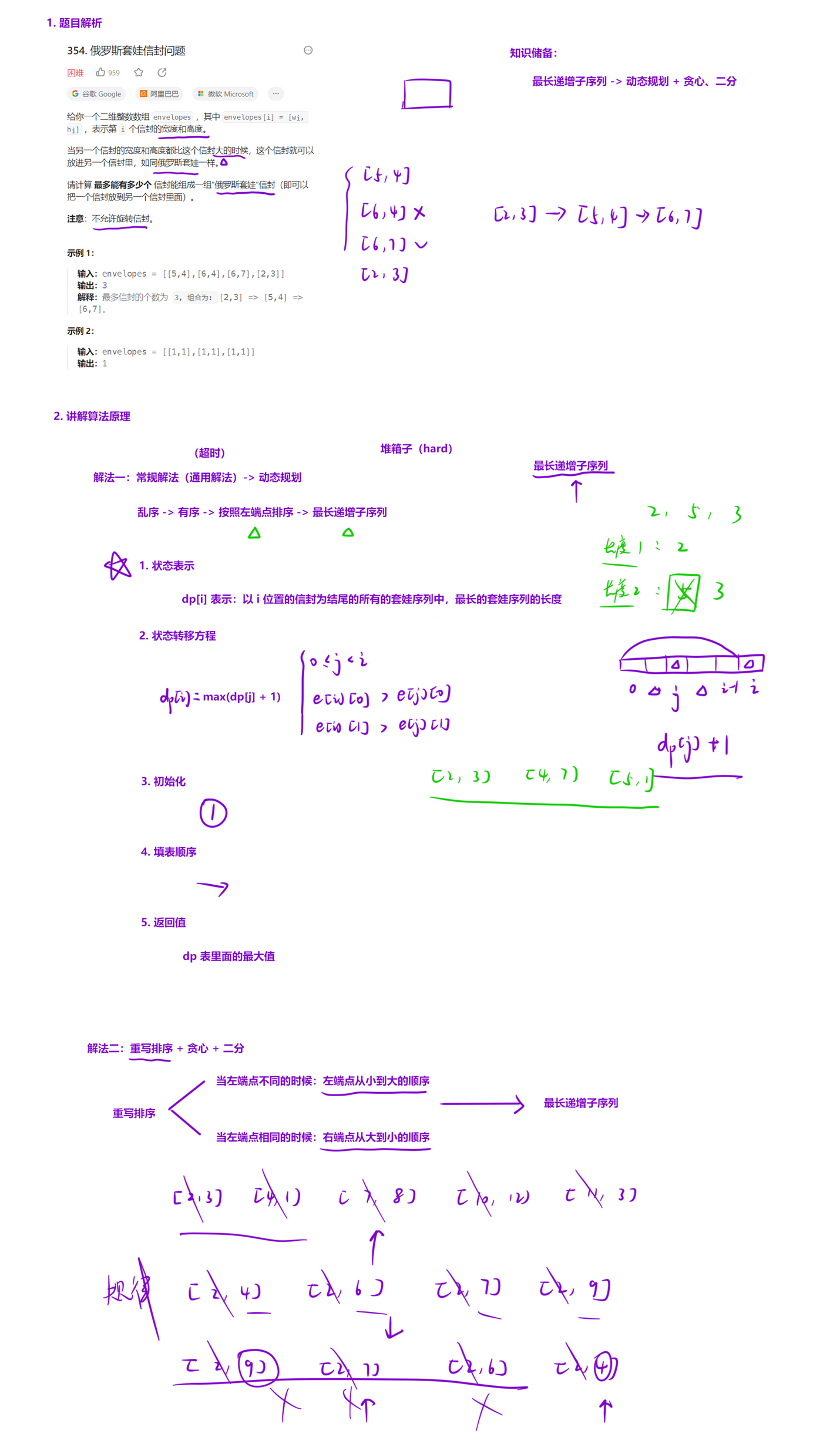
将数组按照左端点排序之后，问题就转化成了最长上升子序列模型，那接下来我们就可以用解决最长上升子序列的经验，来解决这个问题（虽然会超时，但是还是要好好写代码）。

状态表示：

dp[i] 表示：以 i 位置的信封为结尾的所有套娃序列中，最长的套娃序列的长度；

状态转移方程：

dp[i] = max(dp[j] + 1) 其中 0 <= j < i && e[i][0] > e[j][0] && e[i][1] > e[j][1]；

初始化：

全部初始化为 1；

填表顺序：

从左往右；

返回值：

整个 dp 表中的最大值。

解法二（重写排序 + 贪心 + 二分）：

当我们把整个信封按照「下面的规则」排序之后：

i. 左端点不同的时候：按照「左端点从小到大」排序；
ii. 左端点相同的时候：按照「右端点从大到小」排序我们发现，问题就变成了仅考虑信封的「右端点」，完完全全的变成的「最长上升子序列」的模型。那么我们就可以用「贪心 + 二分」优化我们的算法。

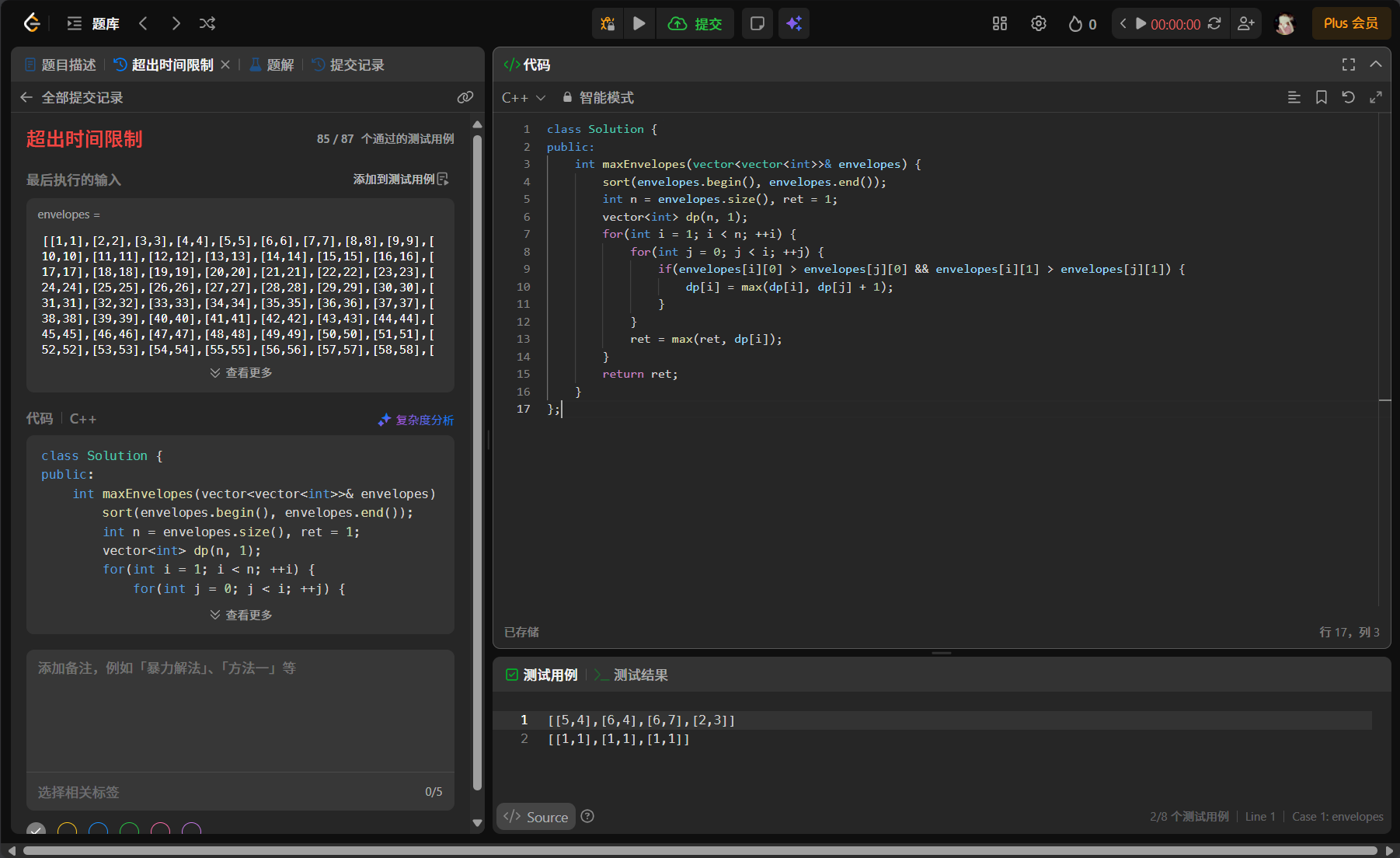
解法一：超时

cpp 复制代码

class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        sort(envelopes.begin(), envelopes.end());
        int n = envelopes.size(), ret = 1;
        vector<int> dp(n, 1);
        for(int i = 1; i < n; ++i) {
            for(int j = 0; j < i; ++j) {
                if(envelopes[i][0] > envelopes[j][0] && envelopes[i][1] > envelopes[j][1]) {
                    dp[i] = max(dp[i], dp[j] + 1);
                }
            }
            ret = max(ret, dp[i]);
        }
        return ret;
    }
};

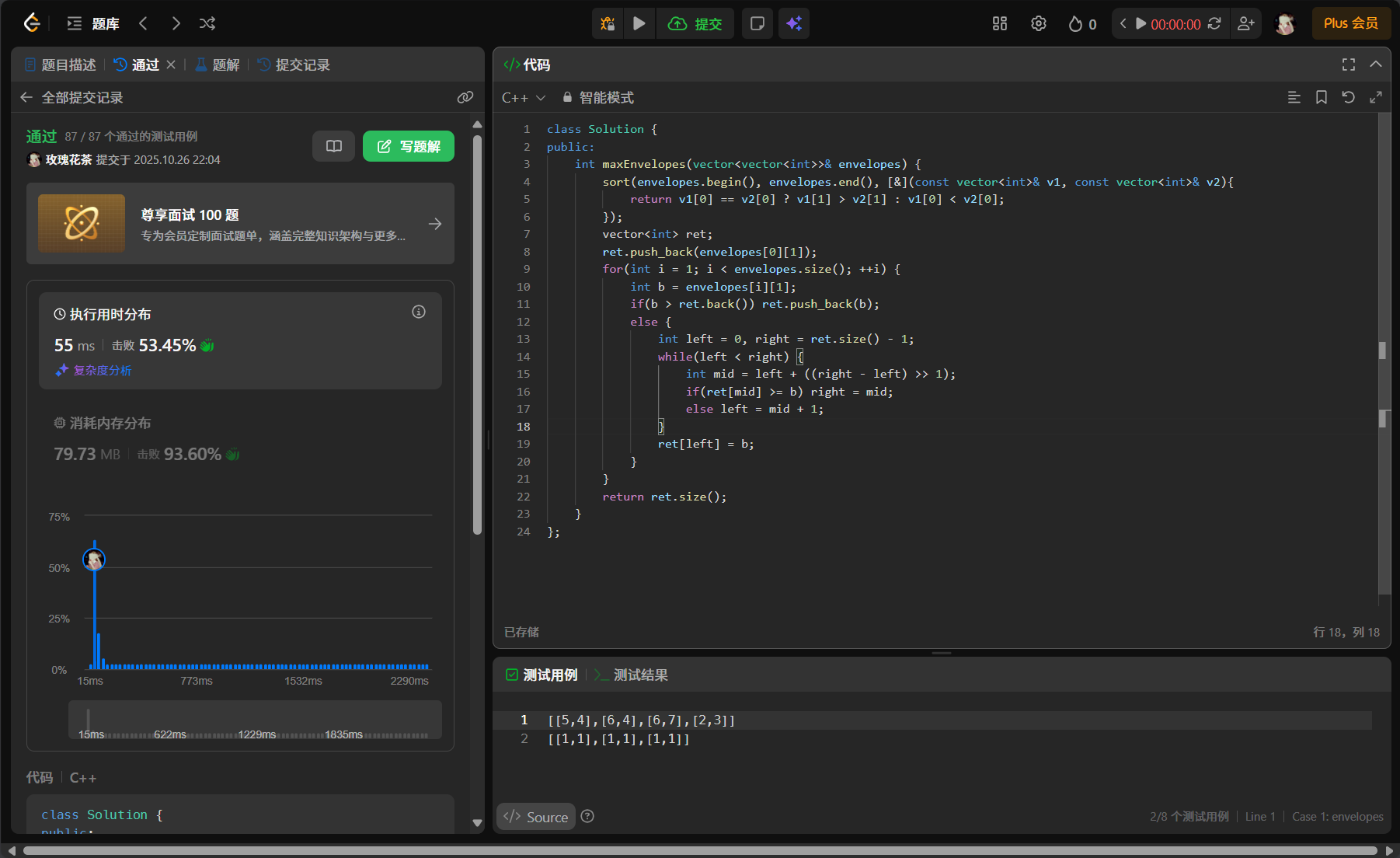
解法二：

cpp 复制代码

class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        sort(envelopes.begin(), envelopes.end(), [&](const vector<int>& v1, const vector<int>& v2){
            return v1[0] == v2[0] ? v1[1] > v2[1] : v1[0] < v2[0]; 
        });
        vector<int> ret;
        ret.push_back(envelopes[0][1]);
        for(int i = 1; i < envelopes.size(); ++i) {
            int b = envelopes[i][1];
            if(b > ret.back()) ret.push_back(b);
            else {
                int left = 0, right = ret.size() - 1;
                while(left < right) {
                    int mid = left + ((right - left) >> 1);
                    if(ret[mid] >= b) right = mid;
                    else left = mid + 1;
                }
                ret[left] = b;
            }
        }
        return ret.size();
    }
};

1262. 可被三整除的最大和 - 力扣（LeetCode）

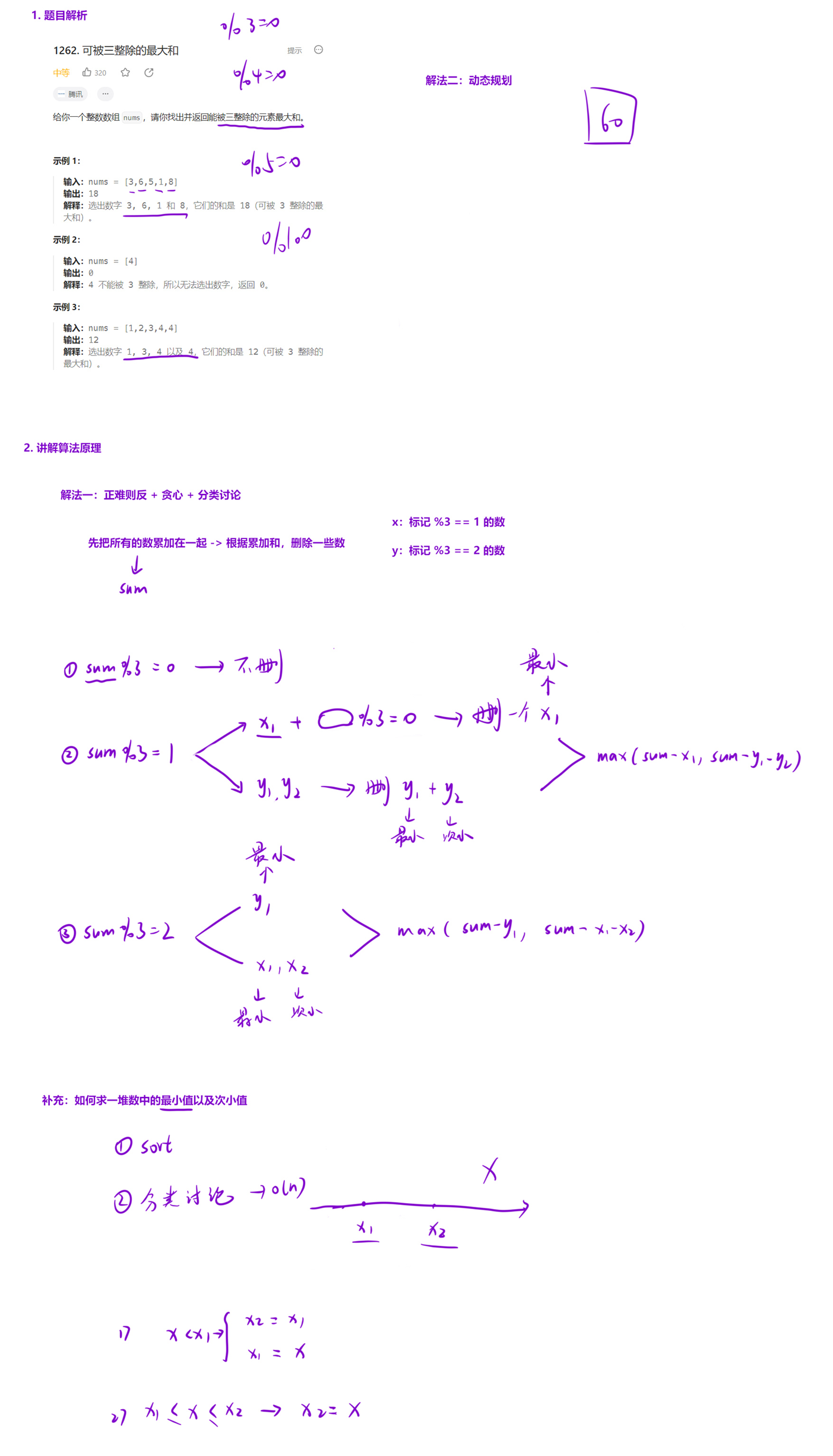
解法（正难则反 + 贪心 + 分类讨论）：

正难则反：

我们可以先把所有的数累加在一起，然后根据累加和的结果，贪心的删除一些数。

分类讨论：

设累加和为 sum，用 x 标记 %3 == 1 的数，用 y 标记 %3 == 2 的数。那么根据 sum 的余数，可以分为下面三种情况：

a. sum % 3 == 0：此时所有元素的和就是满足要求的，那么我们一个也不用删除；
b. sum % 3 == 1 ：此时数组中要么存在一个 x，要么存在两个 y。因为我们要的是最大值，所以应该选择 x 中最小的那个数，记为 x1，或者是 y 中最小以及次小的两个数，记为 y1, y2。那么，我们应该选择两种情况下的最大值：max(sum - x1, sum - y1 - y2)；
c. sum % 3 == 2 ：此时数组中要么存在一个 y，要么存在两个 x。因为我们要的是最大值，所以应该选择 y 中最小的那个数，记为 y1，或者是 x 中最小以及次小的两个数，记为 x1, x2。那么，我们应该选择两种情况下的最大值：max(sum - y1, sum - x1 - x2)；

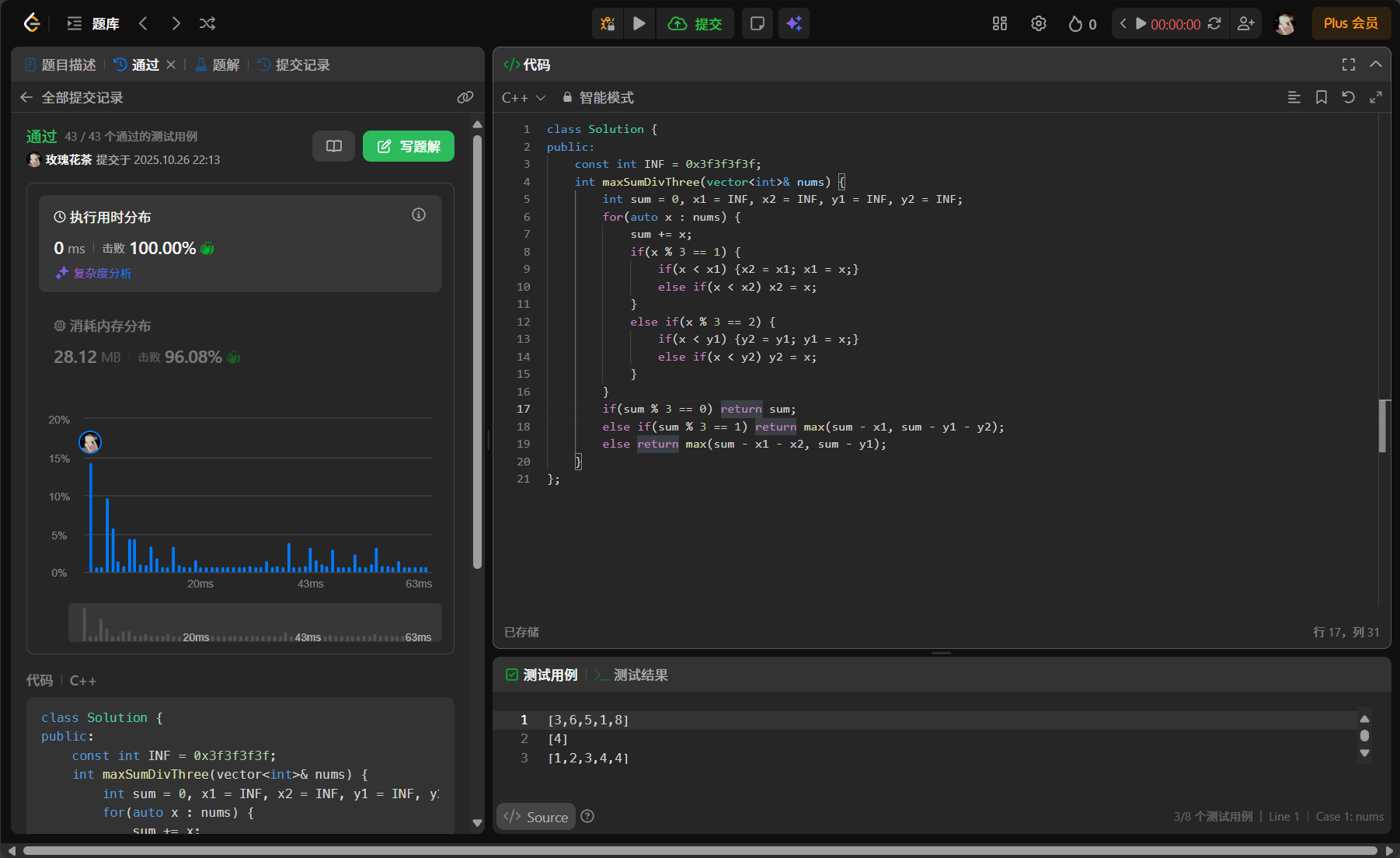
cpp 复制代码

class Solution {
public:
    const int INF = 0x3f3f3f3f;
    int maxSumDivThree(vector<int>& nums) {
        int sum = 0, x1 = INF, x2 = INF, y1 = INF, y2 = INF;
        for(auto x : nums) {
            sum += x;
            if(x % 3 == 1) {
                if(x < x1) {x2 = x1; x1 = x;}
                else if(x < x2) x2 = x;
            }
            else if(x % 3 == 2) {
                if(x < y1) {y2 = y1; y1 = x;}
                else if(x < y2) y2 = x;
            }
        }
        if(sum % 3 == 0) return sum;
        else if(sum % 3 == 1) return max(sum - x1, sum - y1 - y2);
        else return max(sum - x1 - x2, sum - y1);
    }
};

1054. 距离相等的条形码 - 力扣（LeetCode）

解法（贪心）：

贪心策略：

每次处理一批相同的数字，往 n 个空里面摆放；
每次摆放的时候，隔一个格子摆放一个数；
优先处理出现次数最多的那个数。

cpp 复制代码

class Solution {
public:
    vector<int> rearrangeBarcodes(vector<int>& barcodes) {
        unordered_map<int, int> hash;
        int n = barcodes.size(), maxval = 0, maxcnt = 0, index = 0;
        vector<int> ret(n);
        for(auto x : barcodes) {
            ++hash[x];
            if(maxcnt < hash[x]) {
                maxcnt = hash[x];
                maxval = x;
            }
        }
        hash.erase(maxval);
        for(int i = 0; i < maxcnt; ++i) {
            ret[index] = maxval;
            index += 2;
        }
        for(auto [x, y] : hash) {
            for(int i = 0; i < y; ++i) {
                if(index >= n) index = 1;
                ret[index] = x;
                index += 2;
            }
        }
        return ret;
    }
};

767. 重构字符串 - 力扣（LeetCode）

解法（贪心）：

贪心策略：

与上面的一道题解法一致～

cpp 复制代码

class Solution {
public:
    string reorganizeString(string s) {
        int hash[26] = {0};
        char maxChar = ' ';
        int maxCount = 0;
        for (auto ch : s) {
            if (maxCount < ++hash[ch - 'a']) {
                maxChar = ch;
                maxCount = hash[ch - 'a'];
            }
        }
        // 先判断⼀下
        int n = s.size();
        if (maxCount > (n + 1) / 2)
            return "";
        string ret(n, ' ');
        int index = 0;
        // 先处理出现次数最多的那个字符
        for (int i = 0; i < maxCount; i++) {
            ret[index] = maxChar;
            index += 2;
        }
        hash[maxChar - 'a'] = 0;
        for (int i = 0; i < 26; i++) {
            for (int j = 0; j < hash[i]; j++) {
                if (index >= n)
                    index = 1;
                ret[index] = 'a' + i;
                index += 2;
            }
        }
        return ret;
    }
};