算法之动态规划

class Solution {
public:
    int tribonacci(int n) 
    {
        if(n == 0)
        {
            return 0;
        }
        if(n == 2 || n == 1)
        {
            return 1;
        }
        vector<int> dp(n + 1);
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        for(int i = 3; i <= n; i++)
        {
            dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
        }
        return dp[n];
    }
};

三步问题

（1）题目

https://leetcode.cn/problems/three-steps-problem-lcci/description/

（2）解题思路

状态表示：

根据题目dp[i]表示上到第i个台阶的方法种数

状态转移方程

如上图我们以i为结尾来观察以下：dp[i]来源于三个地方dp[i-1] ,dp[i-2],dp[i-3],所以dp[i] = dp[i-1]

dp[i-2] + dp[i-3]

初始化：

我们发现在i等于0,1,2,3的时候,都可以从0开始需要特殊处理,从4开始符合规律

填表顺序：

从左到右

返回值：

从题目上来看dp[n];

（3）代码实现

cpp 复制代码

class Solution {
public:
    int waysToStep(int n) 
    {
        if(n == 1) return 1;
        if(n == 2) return 2;
        if(n == 3) return 4;
        int x = 1e9 + 7;
        vector<int> dp(n + 1);
        dp[0] = 0; 
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 4;
        for(int i = 4; i <= n; i++)
        {
            dp[i] = ((dp[i-1] + dp[i-2] )%x+ dp[i-3])%x;
        }
        return dp[n];
    }
};

最小花费爬楼梯问题

https://leetcode.cn/problems/min-cost-climbing-stairs/description/

（1）题目

（2）解题思路

i此题我会使用两种解题思路

解题思路一：

状态表示：

我们以i位置为结尾来观察 dp[i] 表示到达i位置时，最小的花费

状态转移方程

我们一般使用之前或之前的状态来表示之后的状态来推到出dp[i]的值

根据最近一步来，划分问题：

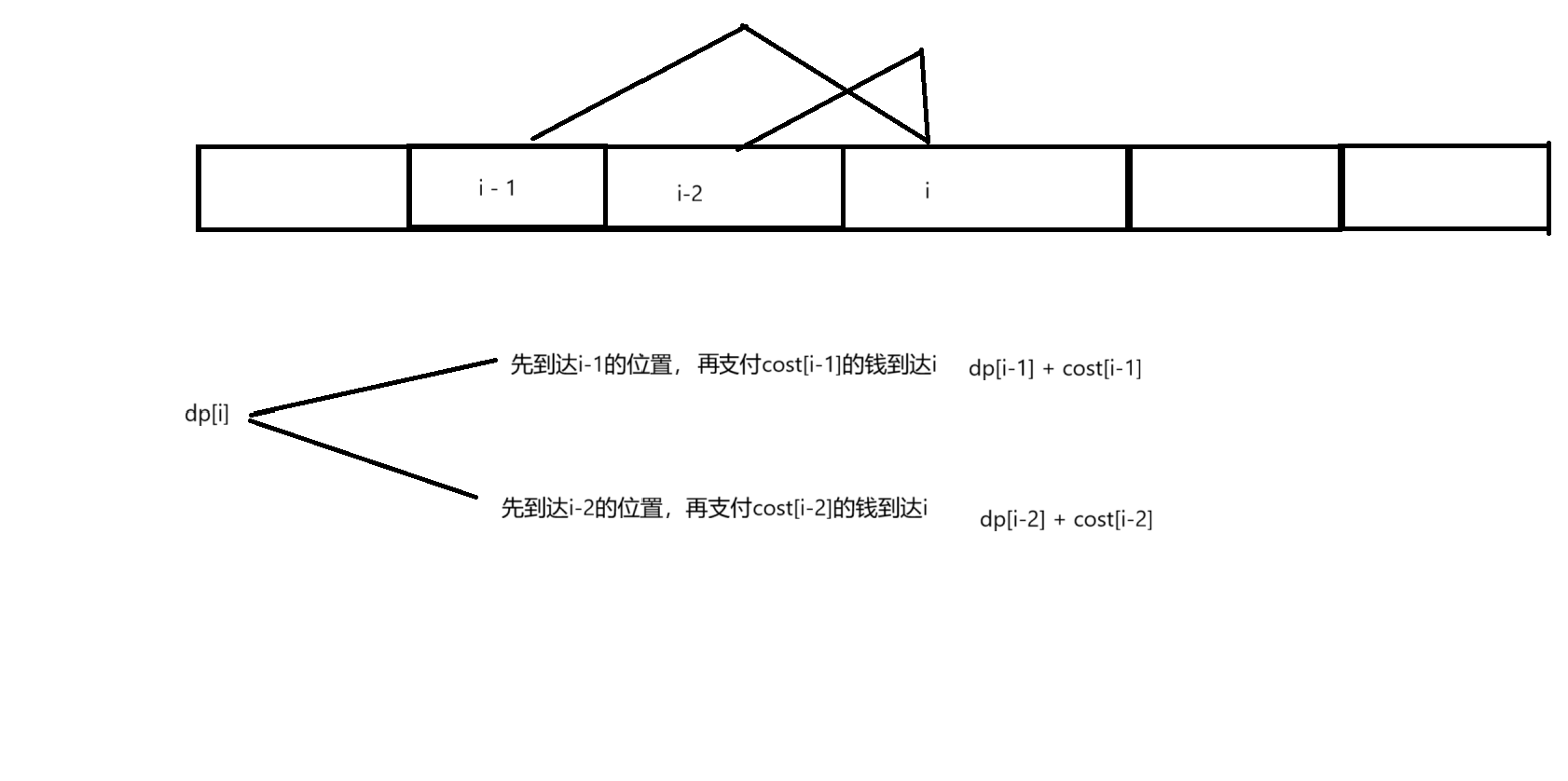
根据上图dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

初始化

由题意值当i等于0或1的时候花费为0

返回值

dp[n]

解题思路二：

状态表示：

以i为起点来思考， dp[i] 表示从i出发，到达楼顶，此时的最小花费

状态转移方程：

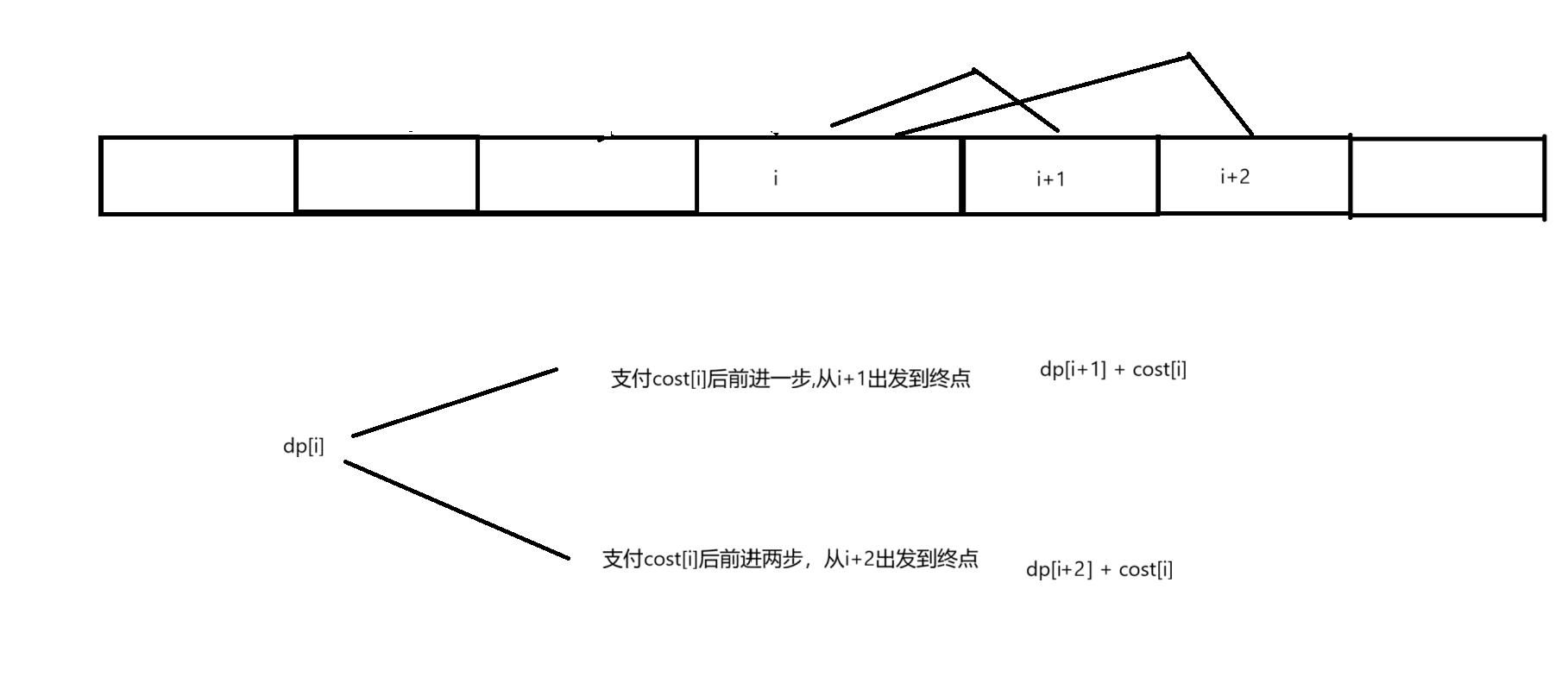
所以dp[i] = min(dp[i+1] + cost[i], dp[i+2] + cost[i])

初始化

我们观察可知当i等于n-1和n-2的时候他们的值是该阶数所花的钱

填表顺序

从右到左

返回值

min(dp[0],dp[1]);

（3）代码实现

注意：终点是n处，所以我们需要多开一个位置

解题一：

cpp 复制代码

class Solution 
{
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {
        int n = cost.size() ;
        vector<int>dp(n + 1);
        for(int i = 2 ; i<=n; i++)
        {
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }

        return dp[n];
    }
};

解法思路二：

cpp 复制代码

class Solution 
{
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {
        int n = cost.size() ;
        vector<int>dp(n + 1);
        dp[n-1] = cost[n-1];
        dp[n-2] = cost[n-2];
        for(int i = n-3 ; i>=0; i--)
        {
            dp[i] = min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
        }

        return min(dp[0],dp[1]);
    }
};

解码方法

https://leetcode.cn/problems/decode-ways/description/

（1）题目

（2）解题思路

状态表示：

我们以i结尾来观察 dp[i]的意思是以i为结尾的时，解码的总数

状态转移方程

距离最近一步，划分问题

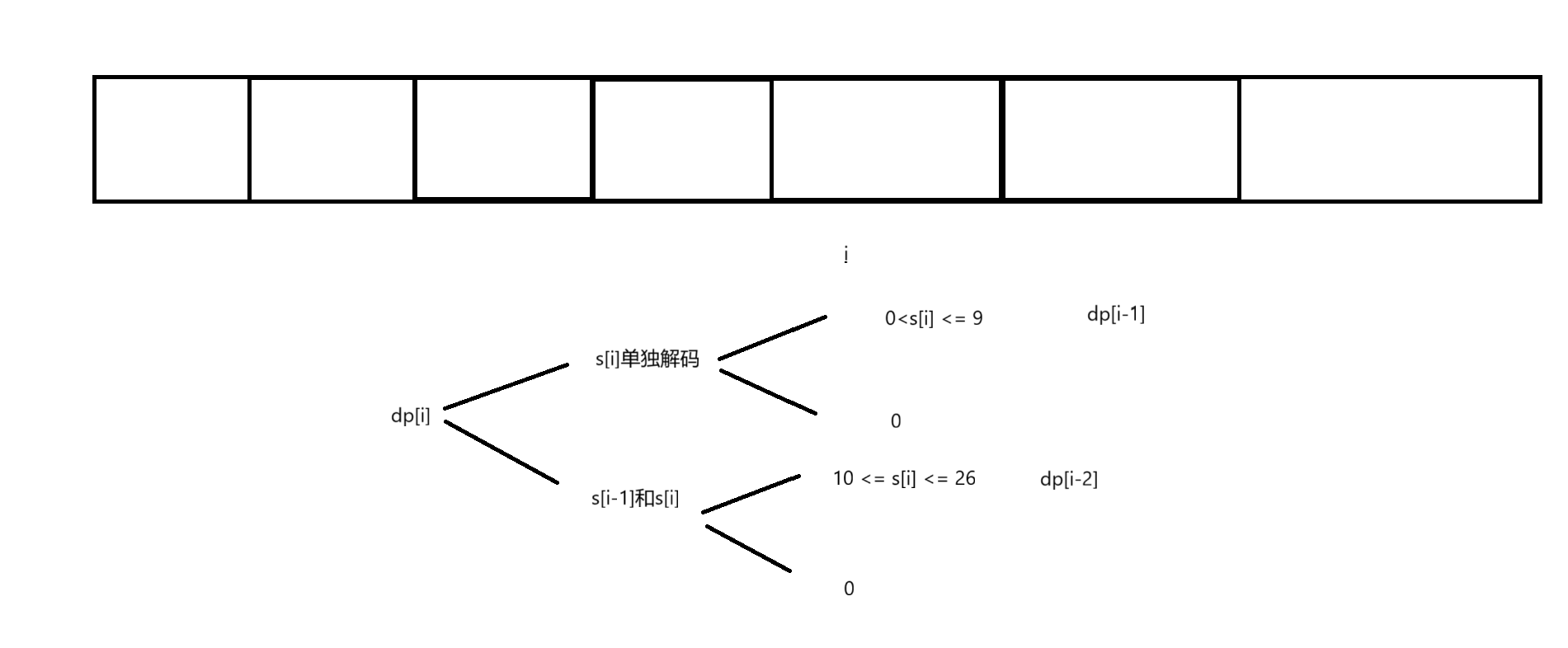
由题意知：dp[i] = dp[i-1] + dp[i+2];

初始化

当i = 0 的时候有两种可能方法为0 或者为1

当i= 1的时候方法可能为0,可能为0，1，或者为1

填表顺序

从左往右

返回值

dp[n-1]

（3）代码实现

cpp 复制代码

class Solution {
public:
    bool check(char i, char j) {
        int x = (i - '0') * 10 + (j - '0');

        if (x >= 10 && x <= 26) {
            return true;
        }
        return false;
    }
    int numDecodings(string s) {
        int n = s.size();
        vector<int> dp(n);
        if (s[0] == '0') {
            return 0;
        } else {
            dp[0] = 1;
        }
        if (n >= 2) {
            if (check(s[0], s[1])) {
                dp[1]++;
            }
            if (s[1] != '0') {
                dp[1]++;
            }
        }
        for (int i = 2; i < n; i++) {
            if (s[i] != '0')
                dp[i] += dp[i - 1];
            if (check(s[i - 1], s[i]))
                dp[i] += dp[i - 2];
        }
        return dp[n - 1];
    }
};

细节：我们关注到我们初始化的需要很多步

如果我们设置一个虚拟节点，导致1的初始化可以通过状态转移方程写出可以节省步骤

注意事项：虚拟节点里面的值，要保证后面的填表是正确的

下标的映射关系

此题的虚拟节点写1

代码实现

cpp 复制代码

class Solution {
public:
    bool check(char i, char j) {
        int x = (i - '0') * 10 + (j - '0');

        if (x >= 10 && x <= 26) {
            return true;
        }
        return false;
    }
    int numDecodings(string s) 
    {

        int n = s.size();
        vector<int> dp(n+1);
         dp[0] = 1;
        if (s[0] == '0') {
            return 0;
        } else {
            dp[1] = 1;
        }
       
        for (int i = 2; i <= n; i++) {
            if (s[i-1] != '0')
                dp[i] += dp[i - 1];
            if (check(s[i - 2], s[i - 1]))
                dp[i] += dp[i - 2];
        }
        return dp[n];
    }
};

不同路径

（1）题目

https://leetcode.cn/problems/unique-paths/

（2）解题思路

状态表示：

如果我们以i,j为结尾，dp[i][j]表示：走到[i,j]位置的时候，一共有多少种方式

状态转移方程

依据最近一步，划分问题

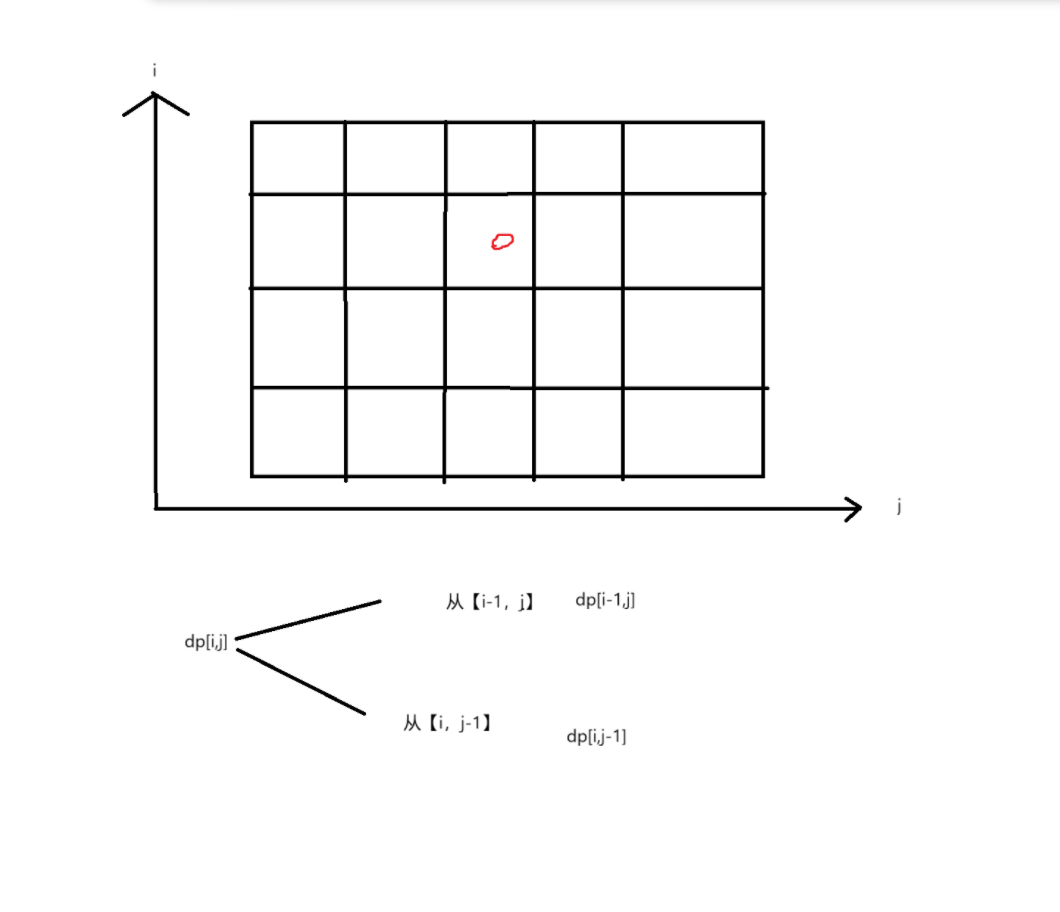
由题意所以dp[i][j] = dp[i-1][j] + dp[i][j-1]

初始化我们观察到i = 0 和 j = 0的时候必须都设为1，这太麻烦了，我们可以使用过上面的虚拟节点发，我们行数和列数都多加上，然后把原来dp[0][0]的附近一个设置为1，这样我们可以发现原i = 0和 j = 0都符合规律

填表顺序

从左到右，从上到下

返回值

dp[m][n]（最结尾处）

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int uniquePaths(int m, int n) 
    {
        vector<vector<int>> dp(m + 1,vector<int>(n + 1));
        dp[1][0] = 1;//会导致原来dp[0][0]的位置为1
        for(int i = 1 ; i <= m; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m][n];
    }
};

不同路径II

https://leetcode.cn/problems/unique-paths-ii/description/

（1）题目

（2）解题思路

这道题和上一道是非类似所以不细说解题思路

状态表示：

以dp[i][j]为结尾，表示到达该位置一共有多少种方法

状态转移方程

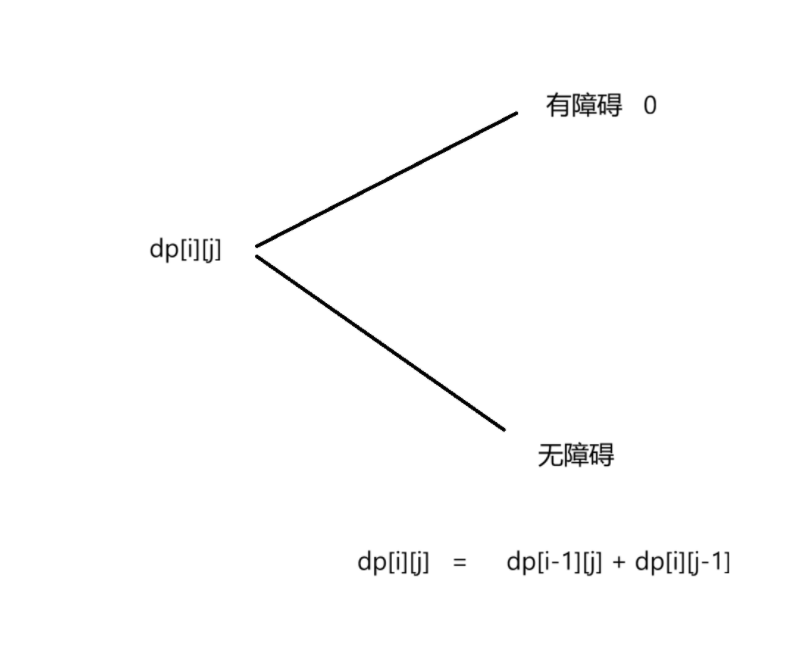
初始化：

同上一道题

填表顺序：

从上到下，从左到右

返回值：

dp[m][n]

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid)
    {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>>dp(m+1,vector<int>(n+1));
        dp[0][1] = 1;
        for(int i = 1; i <= m; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                if(obstacleGrid[i-1][j-1] == 1)
                {
                    dp[i][j]= 0;
                }
                else
                {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }
            }
        }
        return dp[m][n];
    }
};

珠宝价值最高问题

https://leetcode.cn/problems/li-wu-de-zui-da-jie-zhi-lcof/description/

（1）题目

（2）题目解析

状态表示

以【i，j】为结尾，dp[i][j]表示到达[i][j] 位置的时候，此时的最大价值

状态转移方程

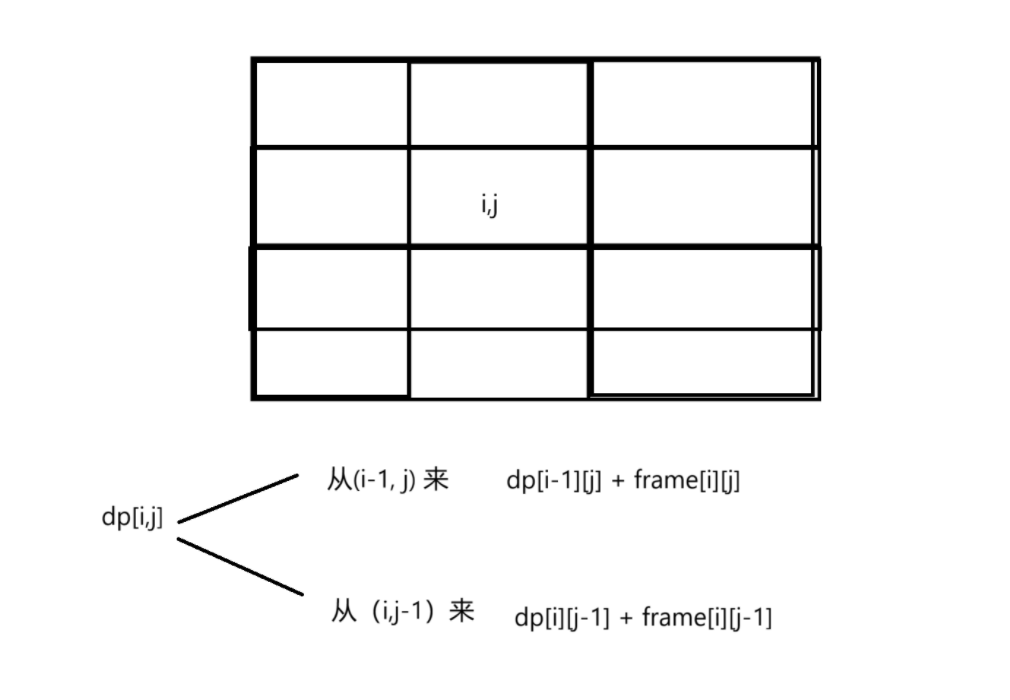
dp[i,j] = max(dp[i-1][j] + frame[i][j], dp[i][j-1] + frame[i][j-1])

初始化

我们类似于设立一排一列虚拟结点，我们要使添加虚拟节点后其他的值是对的所以我们把它设立都设立为0

填表顺序

从左到右，从上到下

返回值

最后一个值

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int jewelleryValue(vector<vector<int>>& frame) 
    {
        int m = frame.size();
        int n = frame[0].size();
        vector<vector<int>> dp (m+1,vector<int>(n+1));
        for(int i = 1; i<=m; i++)
        {
            for(int j = 1; j<=n; j++)
            {
                dp[i][j] = max(dp[i-1][j] + frame[i-1][j-1], dp[i][j-1] + frame[i-1][j-1]);
            }
        }
          return dp[m][n];
    }
};

下降路径最小和

https://leetcode.cn/problems/minimum-falling-path-sum/description/

（1）题目

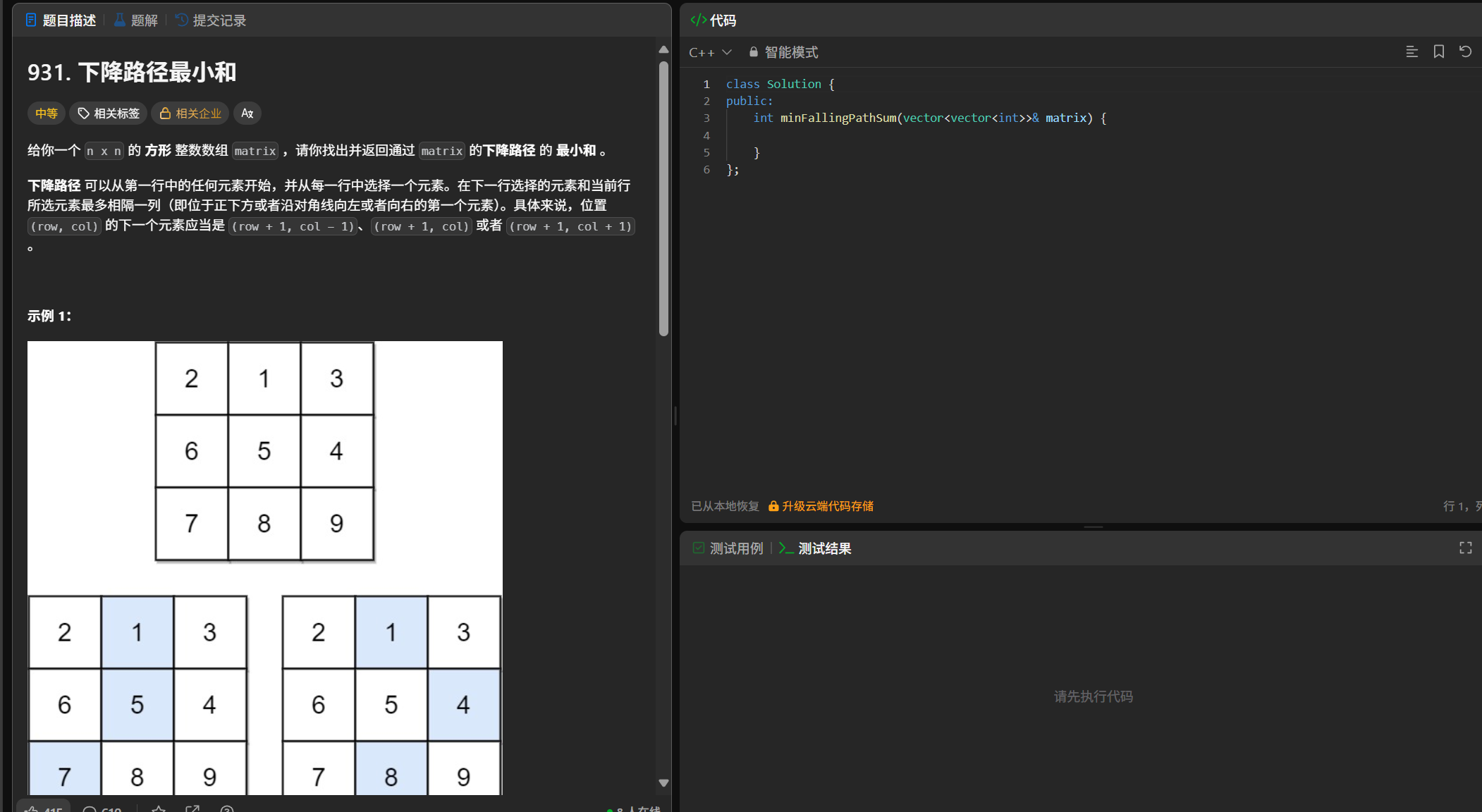
（2）解题思路

状态表示：

以(i,j)结尾，dp[i][j]表示到达[i,j] 位置时，最小的下降路径

状态转移方程

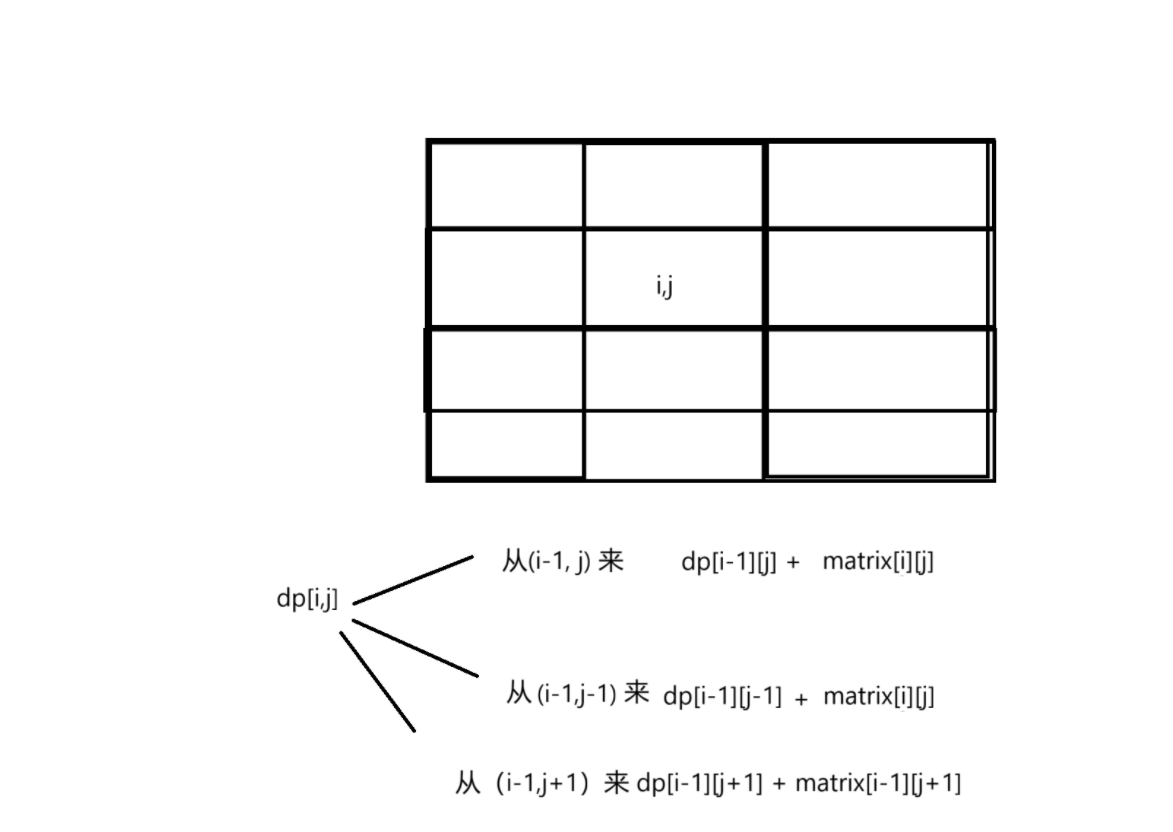
所以dp[i][j]等于他们三个的最小值

初始化

这一道题如果我们设置虚拟结点需要多设置两列，将他们包围在里面

如果我们未设置虚拟结点，那么原第一行的dp 值是他们自己，所以我们将虚拟节点第一行的设置为0，因为寻找的是最小值所以我们将其余的值设置为最大值

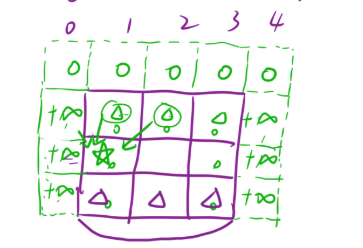
填表顺序

从上到下，从左到右

返回值

最后一行的最大值

（3）代码实现

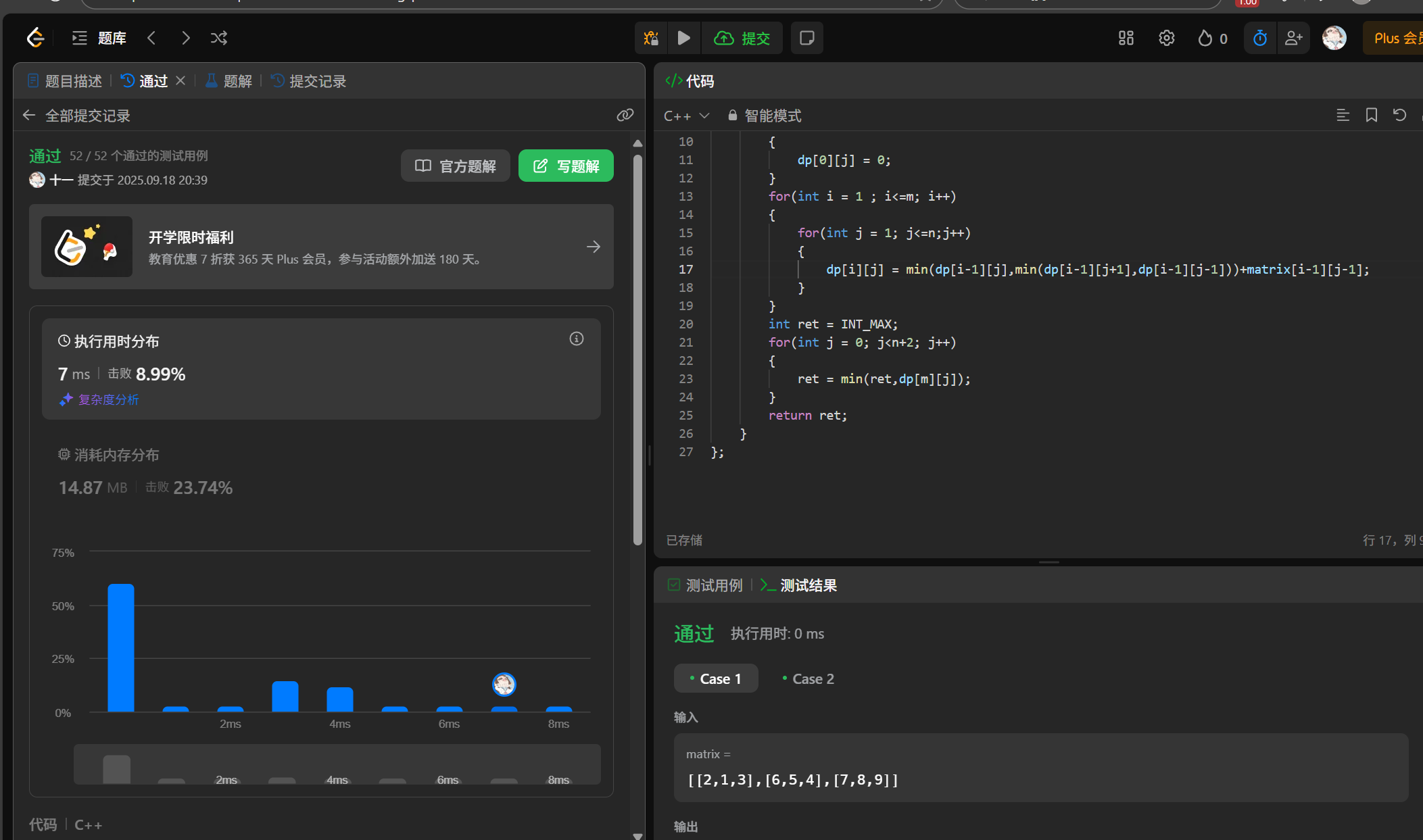
cpp 复制代码

class Solution 
{
public:
    int minFallingPathSum(vector<vector<int>>& matrix) 
    {
        int m = matrix.size();
        int n = m;
        vector<vector<int>>dp(m + 1, vector<int>(n+2,INT_MAX));
        for(int j = 0; j< n+2; j++)
        {
            dp[0][j] = 0;
        }
        for(int i = 1 ; i<=m; i++)
        {
            for(int j = 1; j<=n;j++)
            {
                dp[i][j] = min(dp[i-1][j],min(dp[i-1][j+1],dp[i-1][j-1]))+matrix[i-1][j-1];
            }
        }
        int ret = INT_MAX;
        for(int j = 0; j<n+2; j++)
        {
            ret = min(ret,dp[m][j]);
        }
        return ret;
    }
};

注意如果我们写成 dp[i][j] = min(dp[i-1][j]+matrix[i-1][j-1] ,min(dp[i-1][j+1]+matrix[i-1][j-1],dp[i-1][j-1]+matrix[i-1][j-1]));会越界

最小路径和问题

https://leetcode.cn/problems/minimum-path-sum/description/

（1）题目

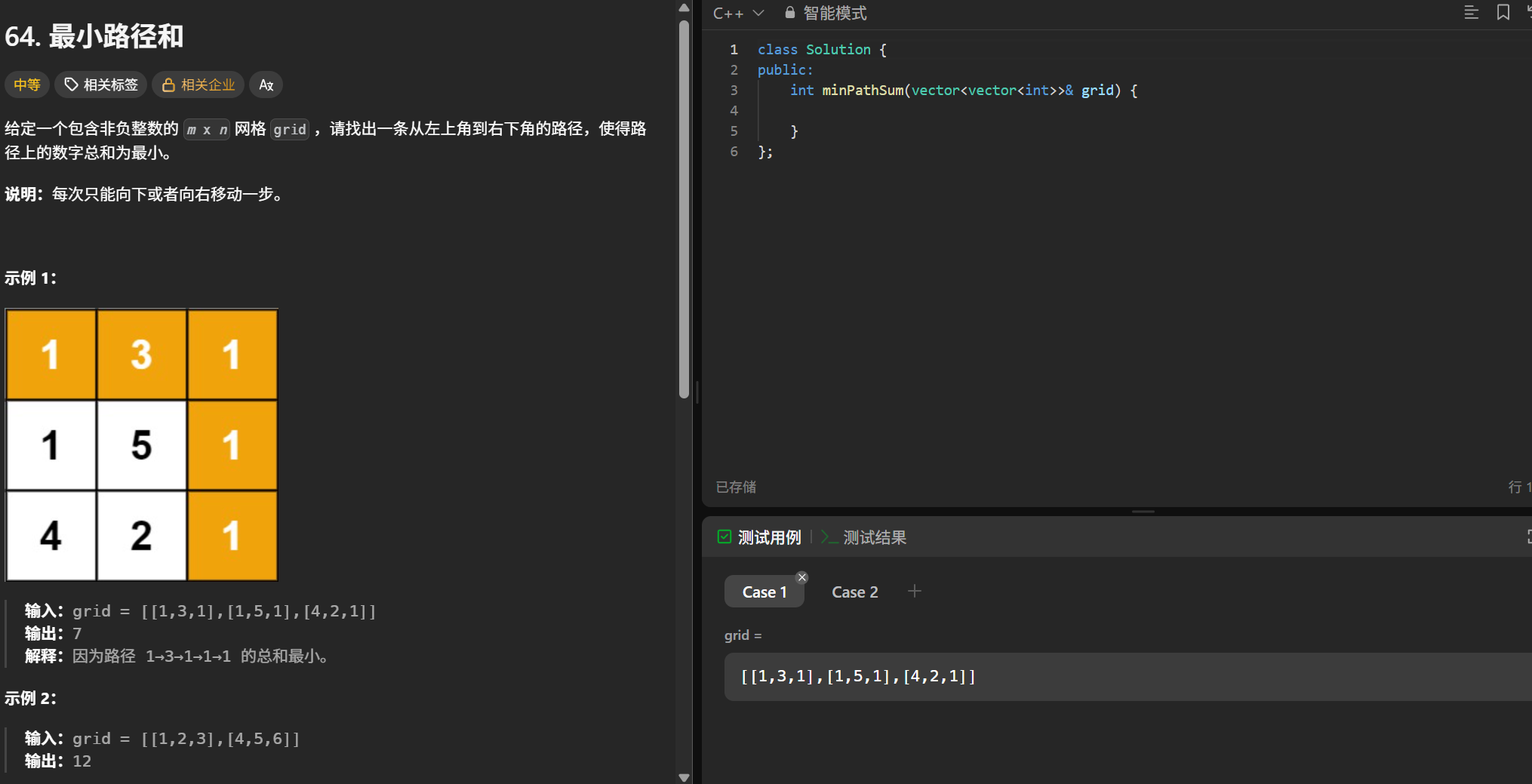
（2）解题思路

状态表示

以[i,j]为结尾，dp[i][j]表示：到达[i,j] 位置时，最小路径和

状态转移方程

根据最近一步，划分问题

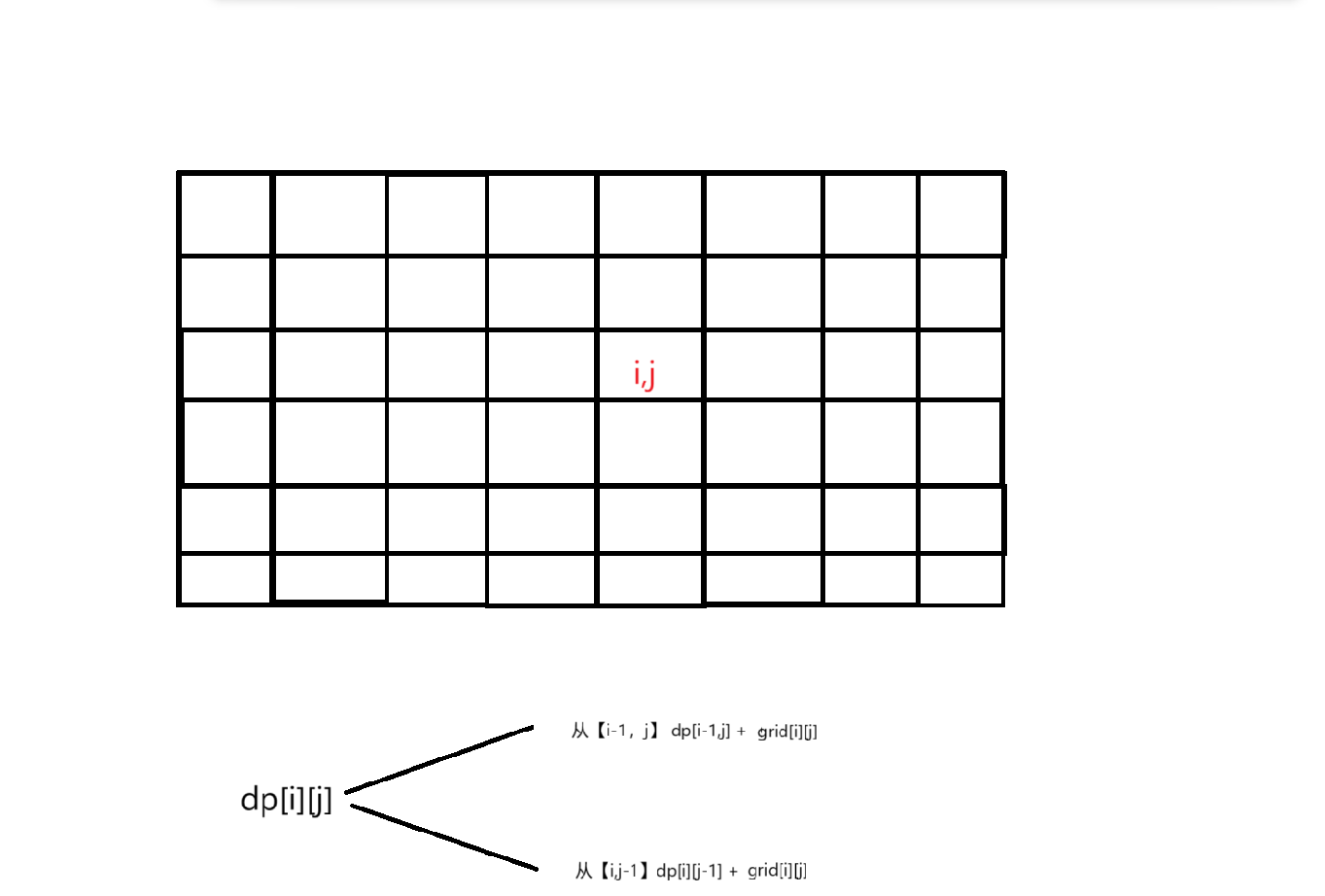
dp[i][j] = min(dp[i][j-1],dp[i-1][j]) + grid[i][j]

初始化

如果我们设置虚拟结点，我们会发现dp[0,1] dp[1,0]需要等于0，因为dp[1][1]需要等于grid[i][j]本身的值

其他的虚拟结点需要设置为INT_MAX,因为他们的值需要取决于它左方的值

填表顺序

从左到右，从上到下

返回值

dp[m][n]

（3）代码实现

cpp 复制代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) 
    {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>>dp(m+1,vector<int>(n+1,INT_MAX));
        dp[0][1] = dp[1][0] = 0;
        for(int i = 1; i<=m; i++)
        {
            for(int j = 1; j<=n; j++)
            {
                dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i-1][j-1];
            }
        }
        return dp[m][n];
    }
};

地下城游戏

https://leetcode.cn/problems/dungeon-game/

（1）题目

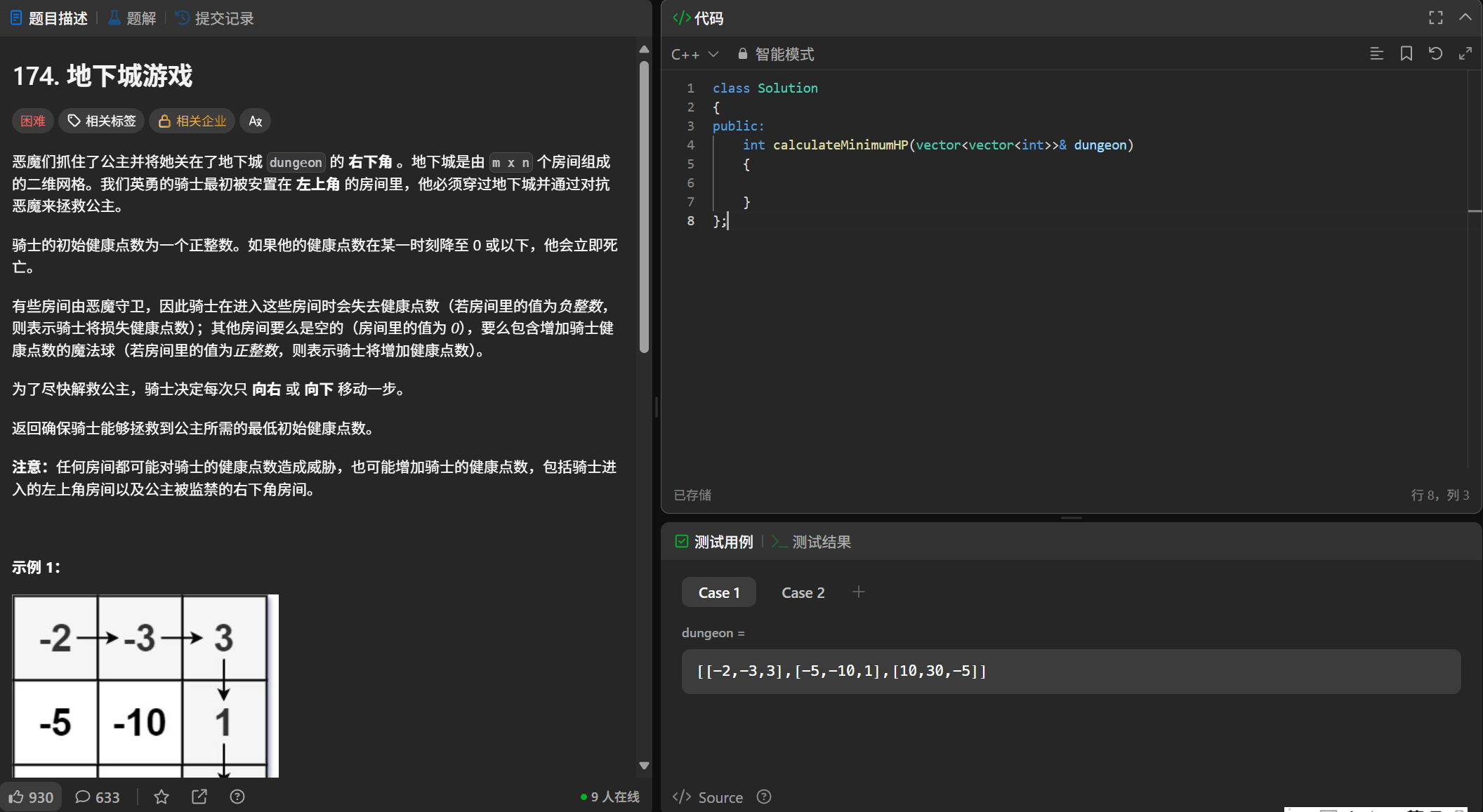
（2）解题思路

状态表示：

如果我们以【i,j】为结尾，dp[i,j]表示：从起点出发，到达【i,j】位置时，所需要的最低健康点数，显然这个思路是错的，健康点数也依靠下一个位置

所以我们以【i,j】为起点，dp[i,j]表示：从[i,j]位置出发，到达终点所需要的最低健康点数

状态转移方程：

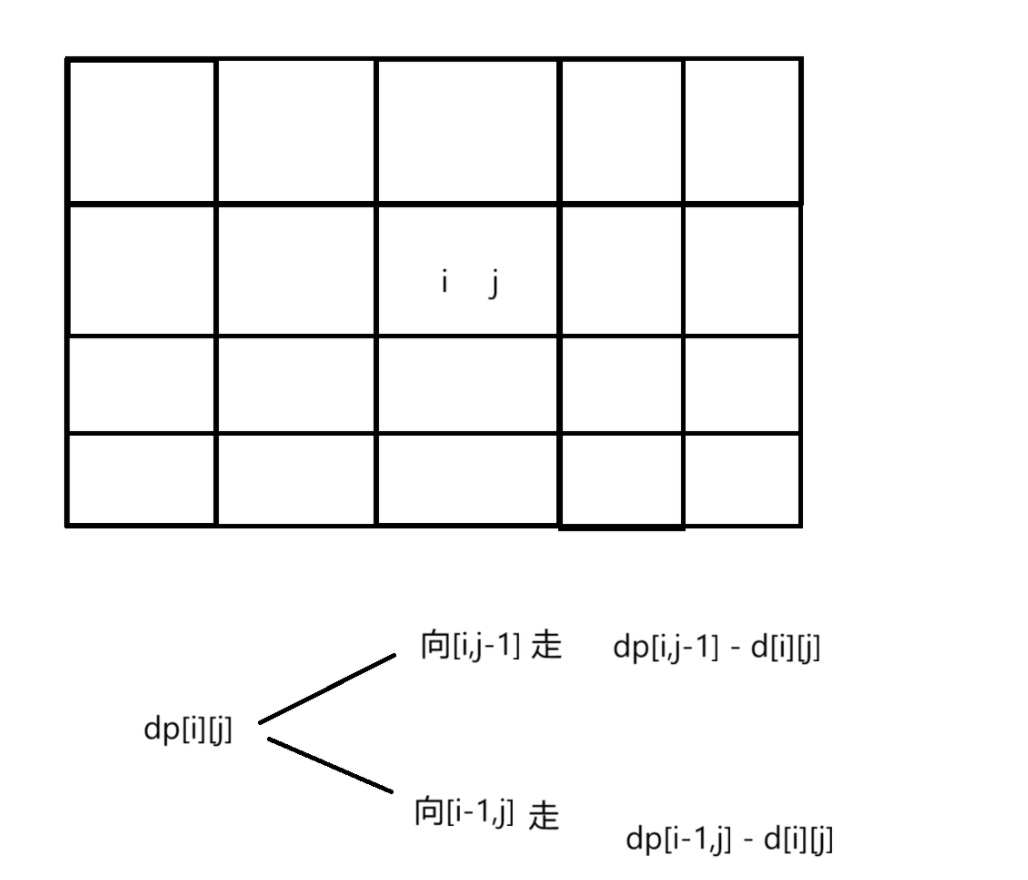
dp[i][j] = min(dp[i][j-1] , dp[i-1][j]) - d[i][j]

如果dp[i][j]是负数，它的结果为1

初始化

因为我们是从右往左，从下往上，所以要在右边和下边添加虚拟结点

dp[m][n] 的结果是d[m][n]的正整数+1所以它的下面和右边的虚拟节点设置为1

其余设置为正无穷

填表顺序

从左到右，从上到下

返回值

dp[0][0]

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int calculateMinimumHP(vector<vector<int>>& dungeon) 
    {
        int m = dungeon.size();
        int n = dungeon[0].size();
        vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));
        dp[m-1][n] =  dp[m][n-1] = 1;
        for(int i = m-1; i>=0; i--)
        {
            for(int j = n-1; j>=0; j--)
            {
                dp[i][j] = min(dp[i+1][j],dp[i][j+1]) - dungeon[i][j];
                dp[i][j] = max(1,dp[i][j]);
            }
        }
        return dp[0][0];
    }
};

按摩师

https://leetcode.cn/problems/the-masseuse-lcci/

（1）题目

（2）解题思路

状态表示：

我们以i 为结尾，dp[i]表示：选到i位置的时候，此时的最长预约时长

但是其实i有两种情况选他和不选他，所以我们需要创建两张表

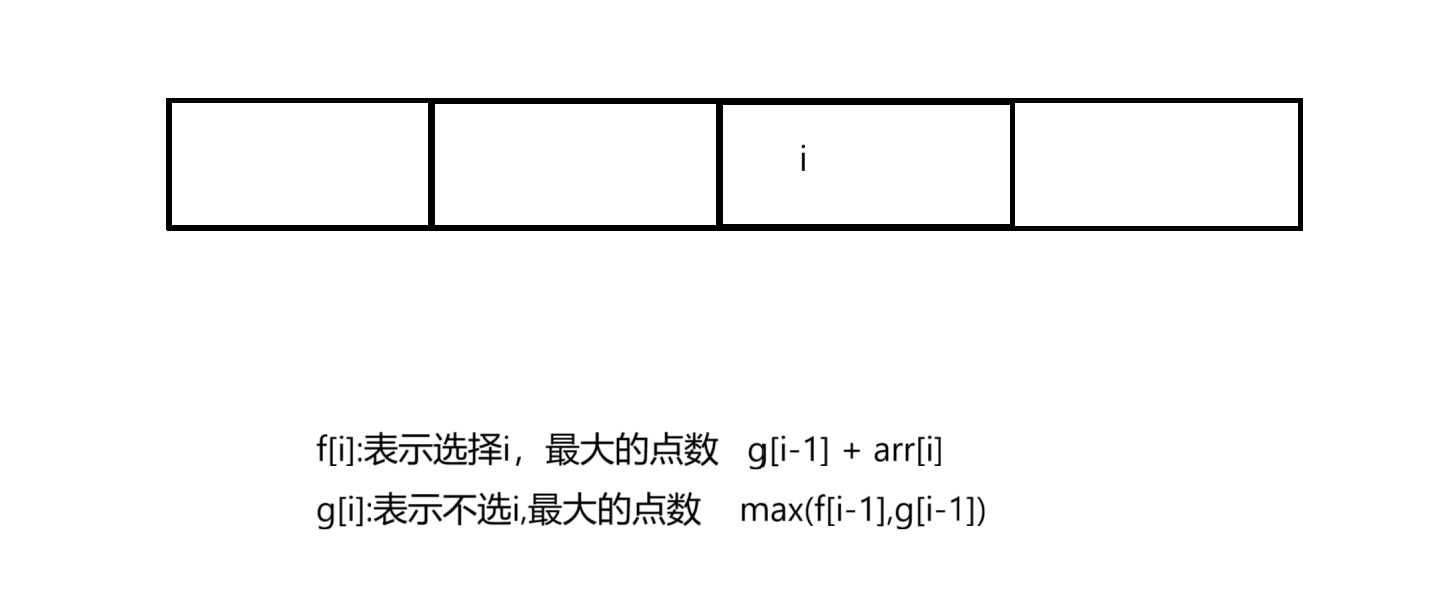
f[i] ：表示选择到i位置的时候，nums[i]必选，此时的最长预约时长

g[i]: 表示选择到i位置的时候，nums[[i]不选，此时的最长预约时长

状态转移方程

f[i] = g[i-1] + nums[i] i

g[i]：有两种情况 i-1 选 g[i] = f[i-1]

i-1不选 g[i] = g[i-1]

初始化

f[0] = nums[0] g[0] = 0

填表顺序

从左到右

返回值

max(f[n-1],g[n-1])

（3）代码实现

cpp 复制代码

class Solution {
public:
    int massage(vector<int>& nums) 
    {
        int n = nums.size();
        if(n == 0) return 0;
        vector<int>f(n);
        vector<int>g(n);
        f[0] = nums[0];
        for(int i = 1; i<n; i++)
        {
            f[i] = g[i-1] + nums[i];
            g[i] = max(g[i-1], f[i-1]);
        }
        return max(g[n-1],f[n-1]);
    }
};

打家劫舍II

https://leetcode.cn/problems/PzWKhm/description/

（1）题目

（2）解题思路

这道题和上一道题十分的相似，唯一的不同是，他是环形，但是我们可以让他变成线性的

如果我们第一个位置不选那我们就可以在（1，n-1）个位置上随便选（即上一道题）

如果我们第一个位置选那我们就可以在（2,n-2）个位置上随便选（即上一道题）

（3）代码实现

cpp 复制代码

class Solution
{
public:
    int n;
    int rob(vector<int>& nums) 
    {
         n = nums.size();
        return max(rob1(nums,2,n-2)+nums[0],rob1(nums,1,n-1));
    }
    int rob1(vector<int>& nums,int left,int right)
    {
        if(left>right) return 0;
        vector<int>f(n);
        vector<int>g(n);
        f[left] = nums[left];
        for(int i = left+1; i<=right; i++)
        {
            f[i] = g[i-1] + nums[i];
            g[i] = max(g[i-1], f[i-1]);
        }
        return max(g[right],f[right]);
    }
};

删除并获取点数

https://leetcode.cn/problems/delete-and-earn/description/

（1）题目

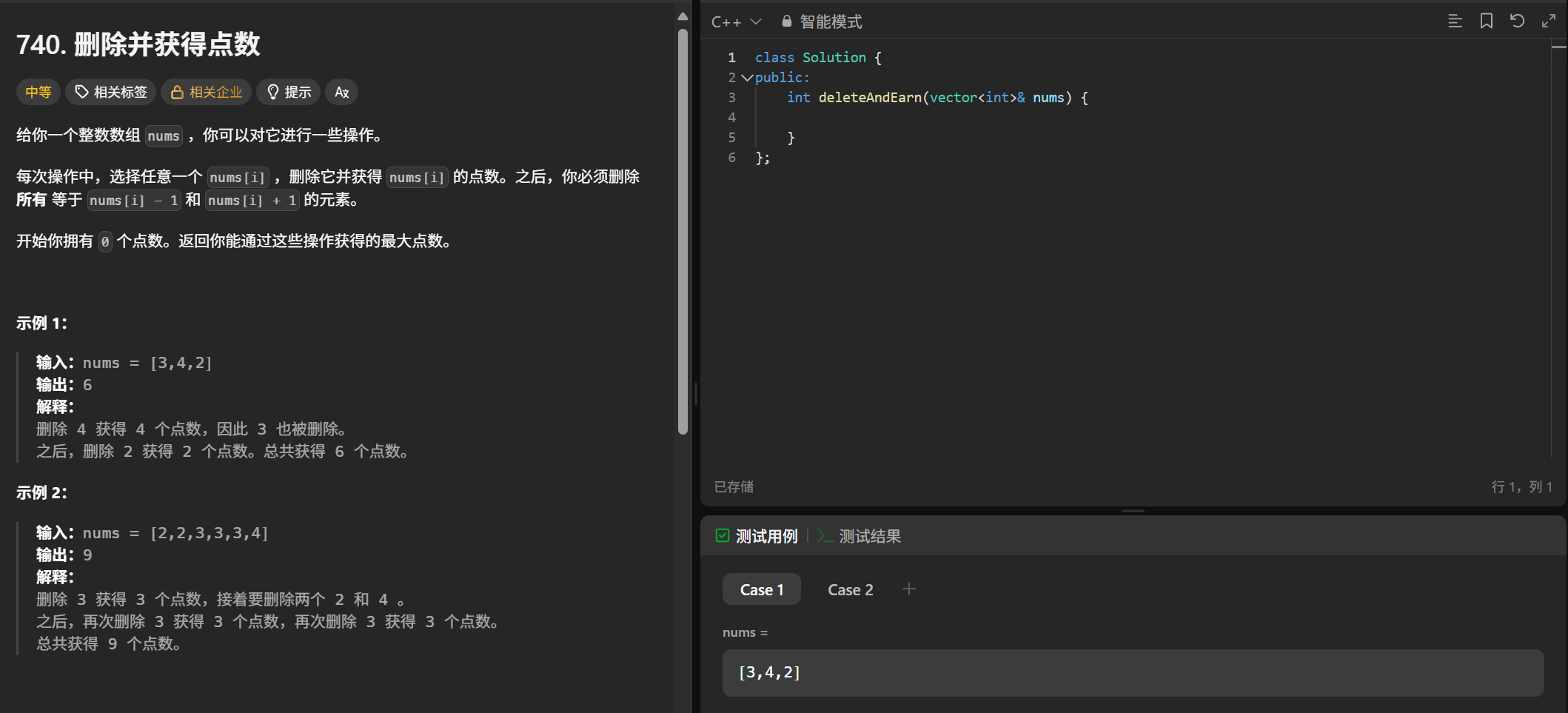
（2）解题思路

这一道题跟打家劫舍问题非常类似，如果可以开辟一个数组，将各个数字的总值放在一个数组中，就是打家劫舍问题

状态表示

以i为结尾，表示选到i最大的点数，他有两种情况，所以我们使用f[i],g[i]表示

初始化

f[0] = arr[0], g[0] = 0;

填表顺序

从左到右，从上到下

返回值

max(f[n-1],g[n-1]);

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int deleteAndEarn(vector<int>& nums) 
    {
        const int N = 10001;
        int arr[N] ={0};
        for(auto &x : nums)
        {
            arr[x] += x;
        }
        vector<int> f(N);
        auto g = f;
        for(int i = 1; i<N; i++)
        {
            f[i] = g[i-1] + arr[i];
            g[i] = max(f[i-1],g[i-1]);
        }
        return max(f[N-1],g[N-1]);
    }
};

粉刷房子

https://leetcode.cn/problems/JEj789/

（1）题目

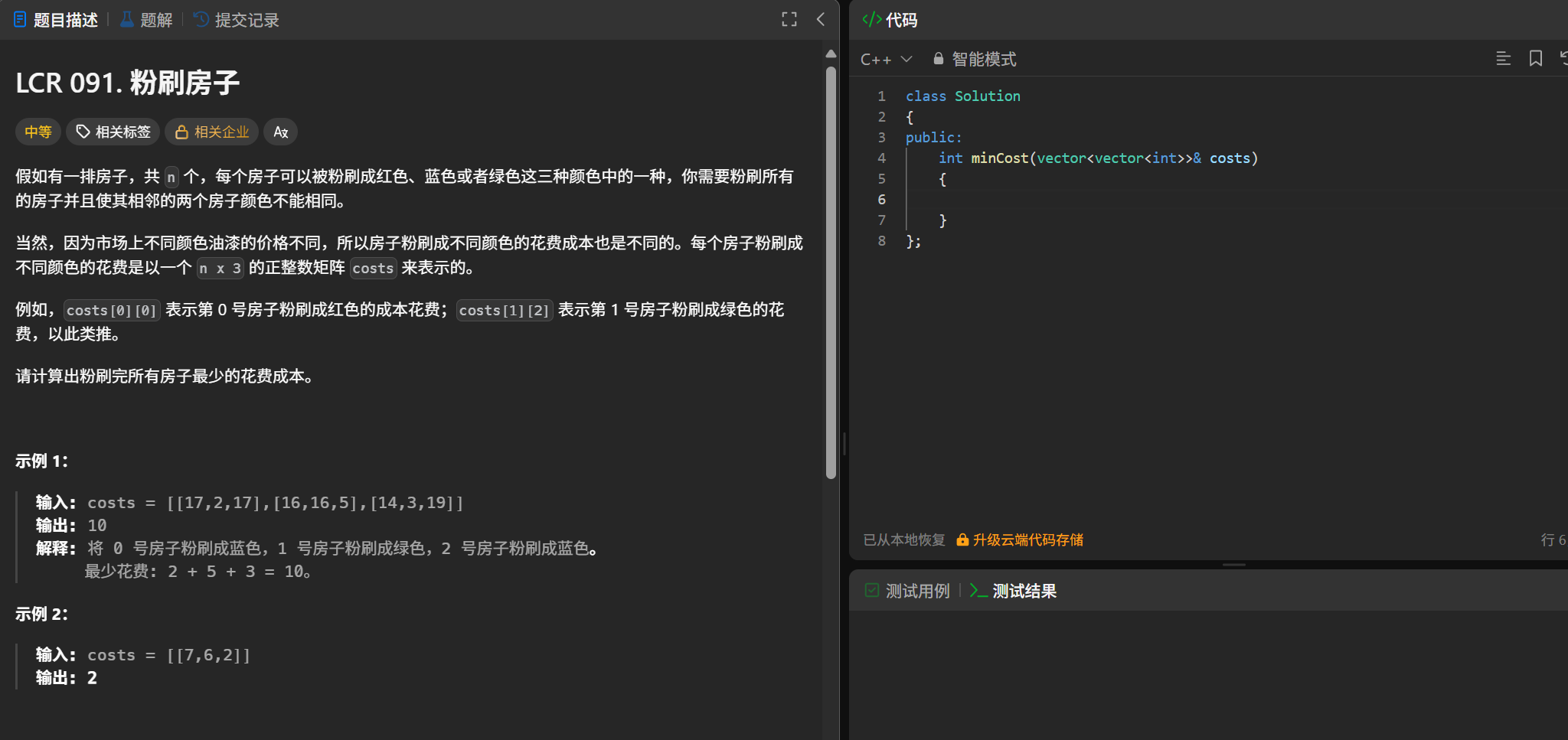
（2）答题思路

状态表示：

我们以i为结尾，dp[i]表示粉刷到的时候，最小的花费

此时我们有三种选择

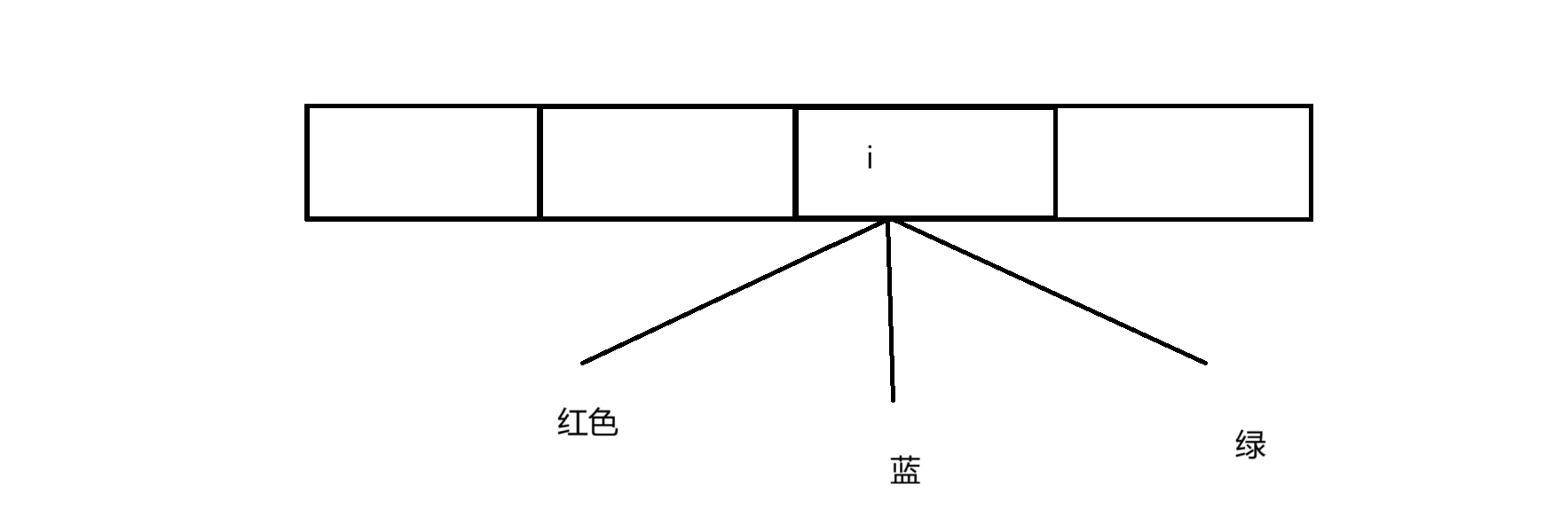
所以我们设置为二维数组

dp[i][0]:表示粉刷i位置，粉刷为红色，此时最小的花费： min(d[i-1][1],d[i-1][2]) + cost[i][0];

dp[i][1]:表示粉刷i位置，粉刷为蓝色，此时最小的花费： min(d[i-1][0],d[i-1][2]) + cost[i][1];

dp[i][2]:表示粉刷i位置，粉刷为绿色，此时最小的花费： min(d[i-1][1],d[i-1][0]) + cost[i][2];

3.初始化

dp[0][0 ]= dp[0][1] = dp[0][2] = 0;

填表顺序

从左到右，从上到下

返回值

min(dp[n][0],min(dp[n][1],dp[n][2]));

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int minCost(vector<vector<int>>& costs) 
    {
        int n = costs.size();
        vector<vector<int>> dp(n+1,vector<int>(3));
        for(int i = 1; i<=n;i++)
        {
            dp[i][0] = min(dp[i-1][1],dp[i-1][2]) + costs[i-1][0];
            dp[i][1] = min(dp[i-1][0],dp[i-1][2]) + costs[i-1][1];
            dp[i][2] = min(dp[i-1][1],dp[i-1][0]) + costs[i-1][2];
        }
        return min(dp[n][0],min(dp[n][1],dp[n][2]));
    }
};

买卖股票的最佳时期

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/description/

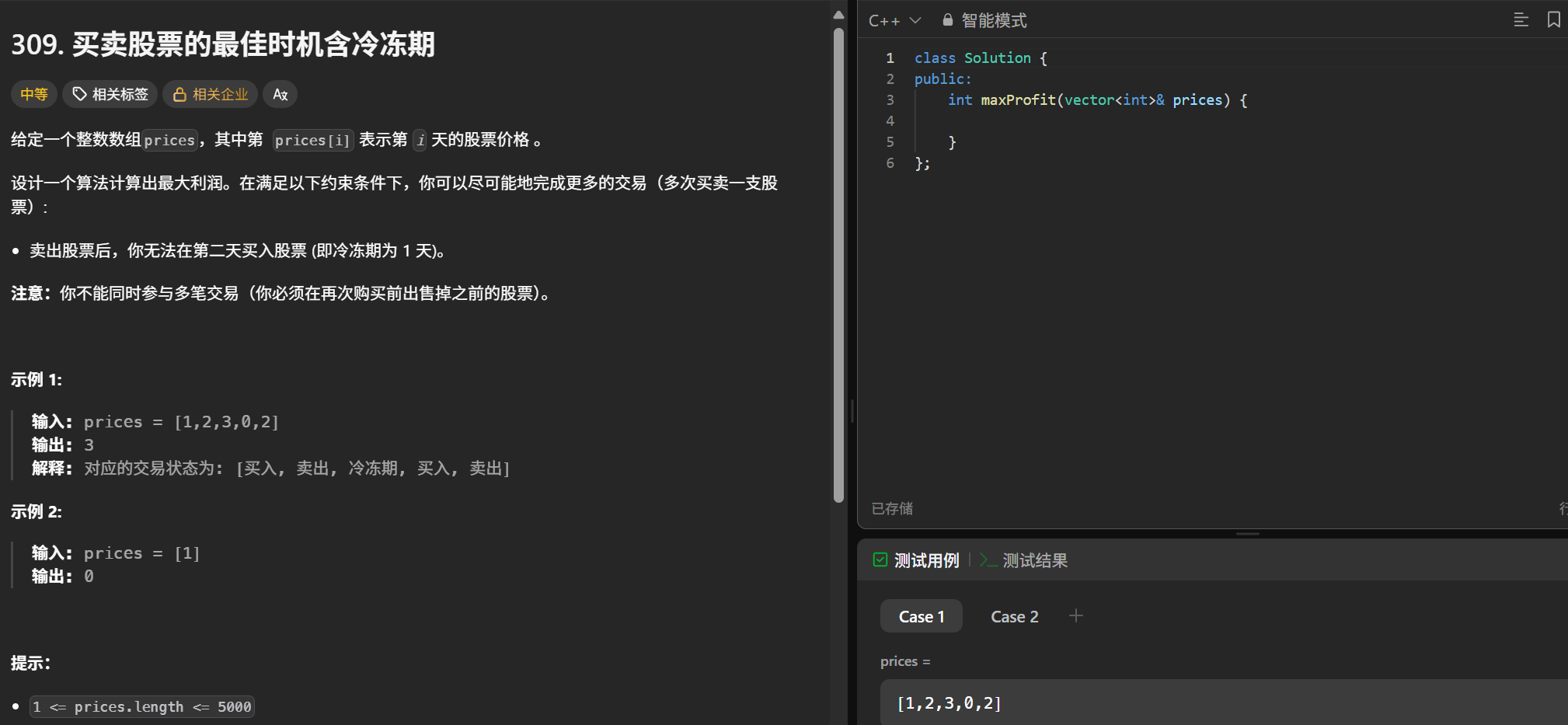
（2）解题思路

状态表示

以i为结尾，表示第i天之后，此时最大的利润

我们发现i有三种状态分别是：买入，可交易，冷冻期

dp[i][0]：表示第i天之后，处于买入状态，此时最大的利润

dp[i][1]：表示第i天之后，处于可交易(手上没有股票)状态，此时最大的利润

dp[i][2]：表示第i天之后，处于冷冻期状态，此时最大的利润

状态表达式

存在多个状态的时候我们使用流程图来表示各个状态的关系

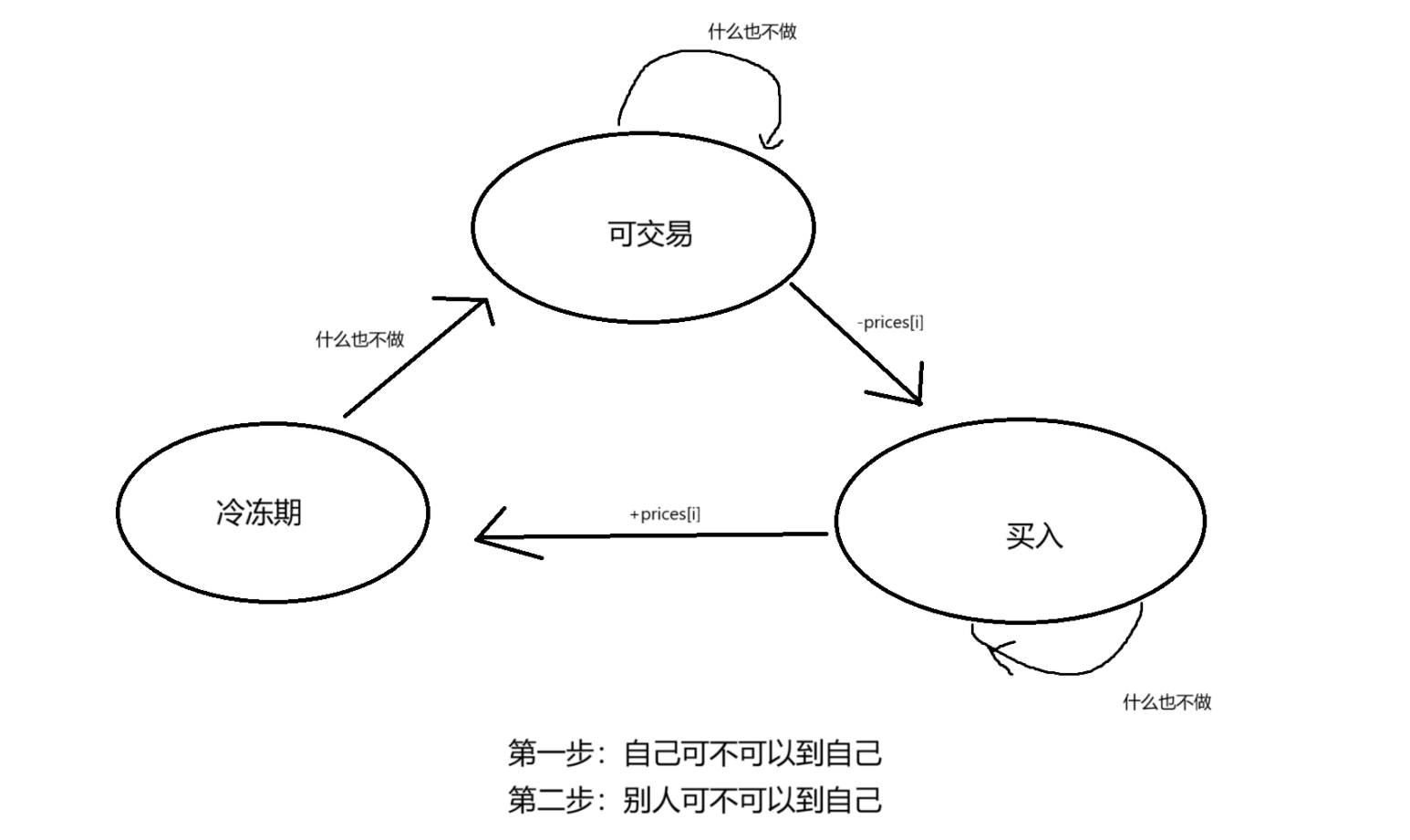
dp[i][0]= max(dp[i-1][0],dp[i-1][1] - prices[i]);

dp[i][1] = max(dp[i-1][1],dp[i-1][2]);

dp[i][2] = dp[i-1][0]+prices[i];

初始化

dp[0][0] = -prices[0]; dp[0][1] = dp[0][1] = 0;

填表顺序

从左到右

返回值

卖完的一定比没卖完的钱多所以

max(dp[m-1][1],dp[m-1][2])

（3）代码实现

cpp 复制代码

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int m = prices.size();
        vector<vector<int>> dp(m, vector<int>(3));
        dp[0][0] = -prices[0];
        for (int i = 1; i < m; i++) 
        {
                dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
                dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
                dp[i][2] = dp[i - 1][0] + prices[i];
        }
        return max(dp[m-1][1],dp[m-1][2]);
    }
};

买卖股票的最佳时期含手续费

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/description/

（1）题目

（2）解题思路

状态表示

以i为结尾，dp[i]表示第i天结束后，所能得到的最佳利润

dp[i]有两种状态：买入（手里有股票），卖出（手里没有股票）因为只收一次手续费，所以设置在买入和卖出都一样，我们设置卖出需要付手续费

dp[i][0]:表示第i天结束后，状态为买入，所能得到的最佳利润。

dp[i][1]:表示第i天结束后，状态为卖出，所能得到的最佳利润。

状态转移方程

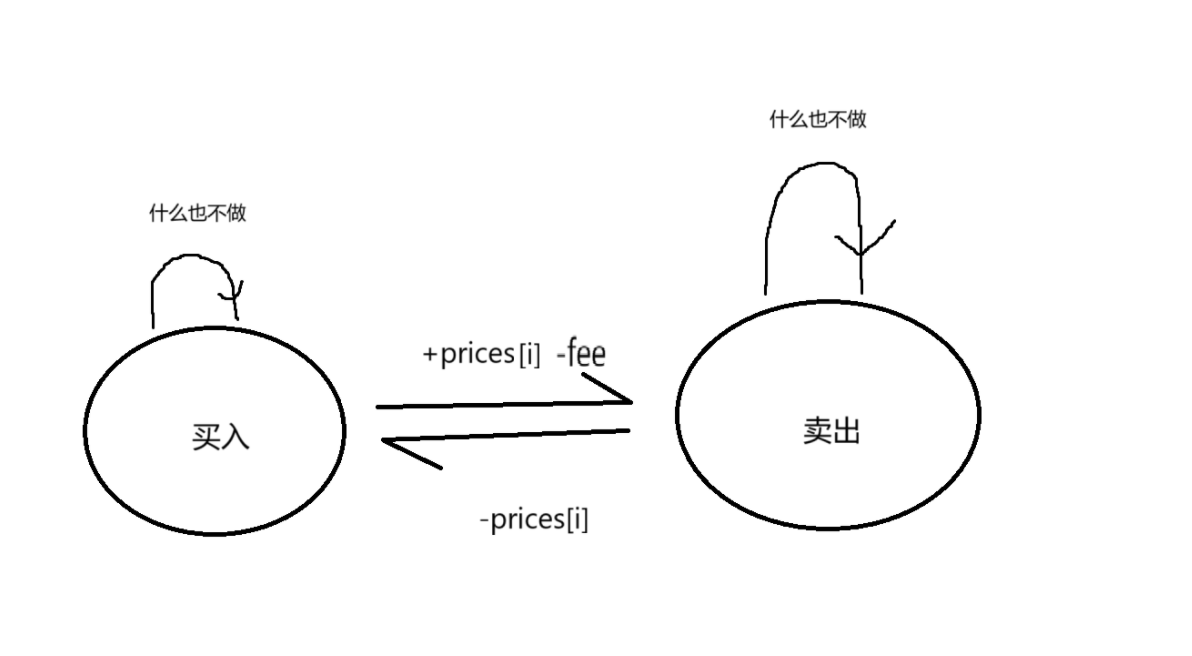
dp[i][0] = max(dp[i-1][0],dp[i-1][1] - prices[i])。

dp[i][1] = max(dp[i-1][1],dp[i-1][0]+prices[i]-fee)。

初始化

dp[0][0] = -prices[0];

dp[0][1] = 0;

填表顺序

从左到右，两个表一起填

返回值

卖完的一定比没卖完的钱多所以

dp[m-1][1];

（3）代码实现

cpp 复制代码

class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) 
    {
        int m = prices.size();
        vector<vector<int>> dp(m, vector<int>(2));
        dp[0][0] = -prices[0];
        for (int i = 1; i < m; i++) 
        {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee);
        }
        return dp[m-1][1];
    }
};

买卖股票的最佳时期III

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/description/

（1）题目

（2）解题思路

状态表示

以i为结尾,dp[i]表示第i天结束后，所能获得的最佳利润

dp[i]有四种状态

f[i][j]: 表示在第i天结束之后，完成了j 次交易，此时处于"买入"状态下的最大利润。

g[i][j]: 表示在第i天结束之后，完成了j 次交易，此时处于"卖出"状态下的最大利润。

转移方程

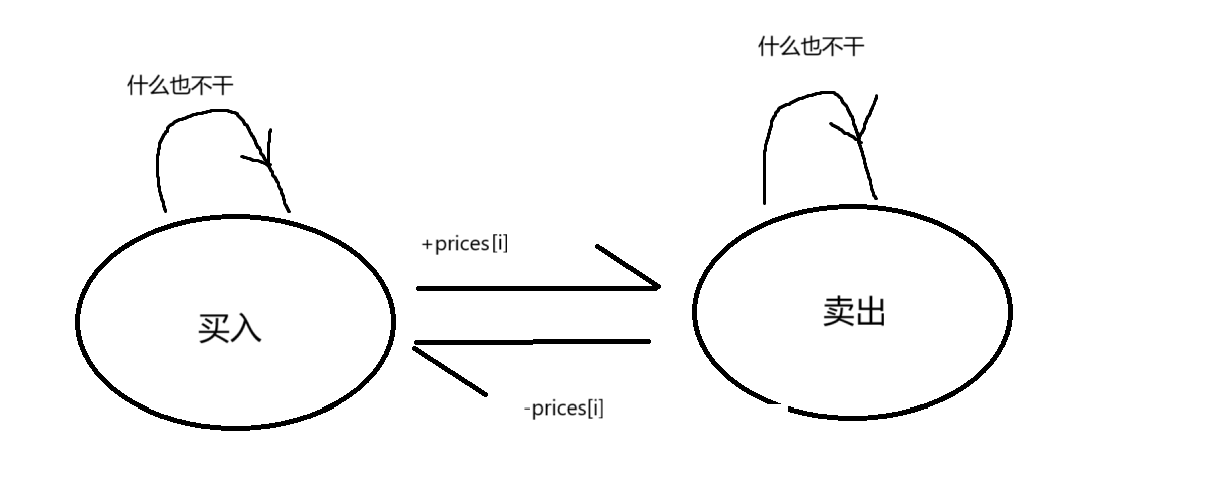
f[i][j] = max(f[i-1][j],g[i-1][j]-prices[i]).

g[i][j] = max(g[i-1][j] , f[i-1][j-1]+prices[i])

初始化

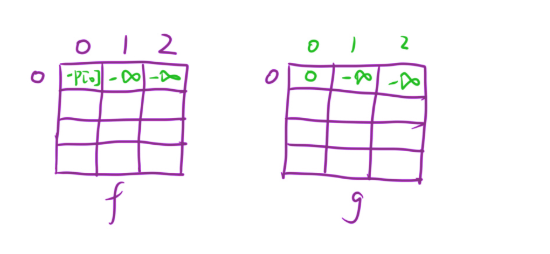
负的无穷大可以是-0*3f3f3f3f

填表顺序

从上到下，从左到右

两个表一起填

返回值

g[m-1][]中的最大值

（3）代码实现

cpp 复制代码

class Solution {
public:
    int maxProfit(vector<int>& prices) 
    {
        int m = prices.size();
        vector<vector<int>> f(m, vector<int>(3, -0x3f3f3f));
        auto g = f;
        f[0][0] = -prices[0];
        g[0][0] = 0;
        for (int i = 1; i < m; i++) 
        {
            for (int j = 0; j < 3; j++) 
            {
                f[i][j] = max(f[i - 1][j], g[i - 1][j] - prices[i]);
                g[i][j] = g[i-1][j];
                if(j>=1)
                {
                    g[i][j] = max(g[i][j],f[i-1][j-1]+prices[i]);
                }

            }
        }
        int ret = 0;
        for(int i = 0; i < 3; i++)
        {
            ret = max(ret,g[m-1][i]);
        }
        return ret;
    }
};

买卖股票的最佳时期

https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/description/

（1）题目

（2）解题思路

状态表示

以i为结尾，dp[i]表示第i天结束之后，所能获得的最大利润

i有两种情况，f[i]表示买入状态，g[i]表示卖出状态

f[i][j]：表示第i天结束之后，完成j次交易，此时处于买入状态，所能获得的最大利润。

g[i][j]：表示第i天结束之后，完成j次交易，此时处于卖出状态，所能获得的最大利润。

状态转移方程

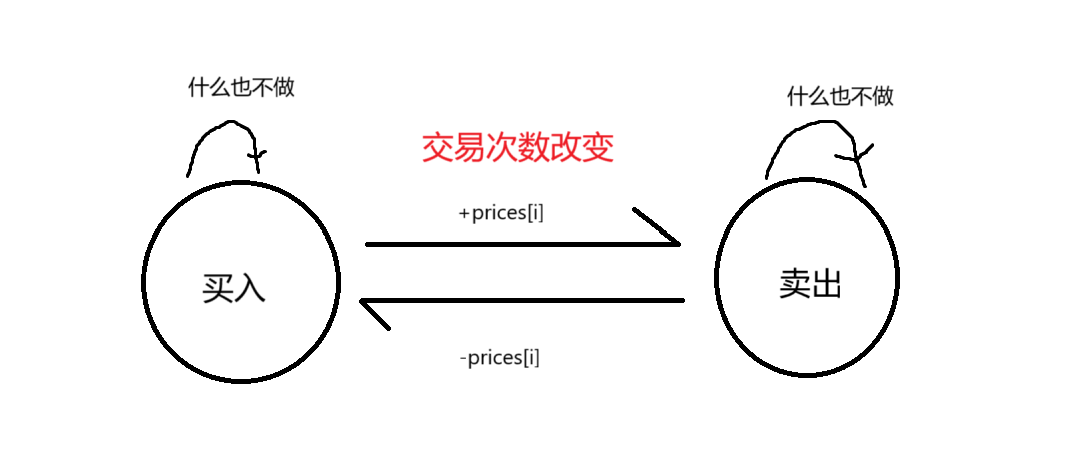
f[i][j] = max（f[i-1][j],g[i-1][j]-prices[i]）。

g[i][j] = max（f[i-1][j-1]+prices[i],g[i-1][j]）注意：i-1需要>=0，因为当i为0的时候他没有前一次交易

初始化

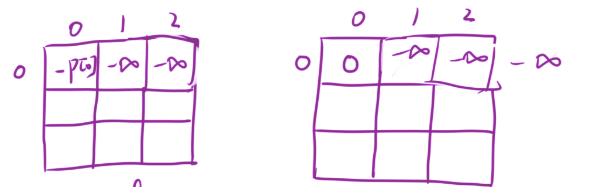
负无穷表示-0x3f3f3f

填表顺序

从上到下，从该左到右，两张表一起填

返回结果

g表的最后一列

细节

k = min(n/2,k)，因为总共只能做n/2次交易

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int maxProfit(int k, vector<int>& prices) 
    {
        int n = prices.size();
        k = min(k, n / 2);
        vector<vector<int>> f(n, vector<int>(k + 1, -0x3f3f3f));
        auto g = f;
        f[0][0] = -prices[0];
        g[0][0] = 0;
        for (int i = 1; i < n; i++) 
        {
            for (int j = 0; j <= k; j++) 
            {
                f[i][j] = max(f[i - 1][j],g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if(j>=1)
                {
                    g[i][j] = max(g[i][j],f[i-1][j-1]+prices[i]);
                }
            }
        }
        int ret = 0;
        for(int i = 0; i<=k; i++)
        {
            ret = max(ret,g[n-1][i]);
        }
        return ret;
    }
};

最大子数组之和

https://leetcode.cn/problems/maximum-subarray/

（1）题目

（2）解题思路

状态表示

以i为结尾，dp[i]表示以i为结尾的所有子数组的最大值

状态转移方程

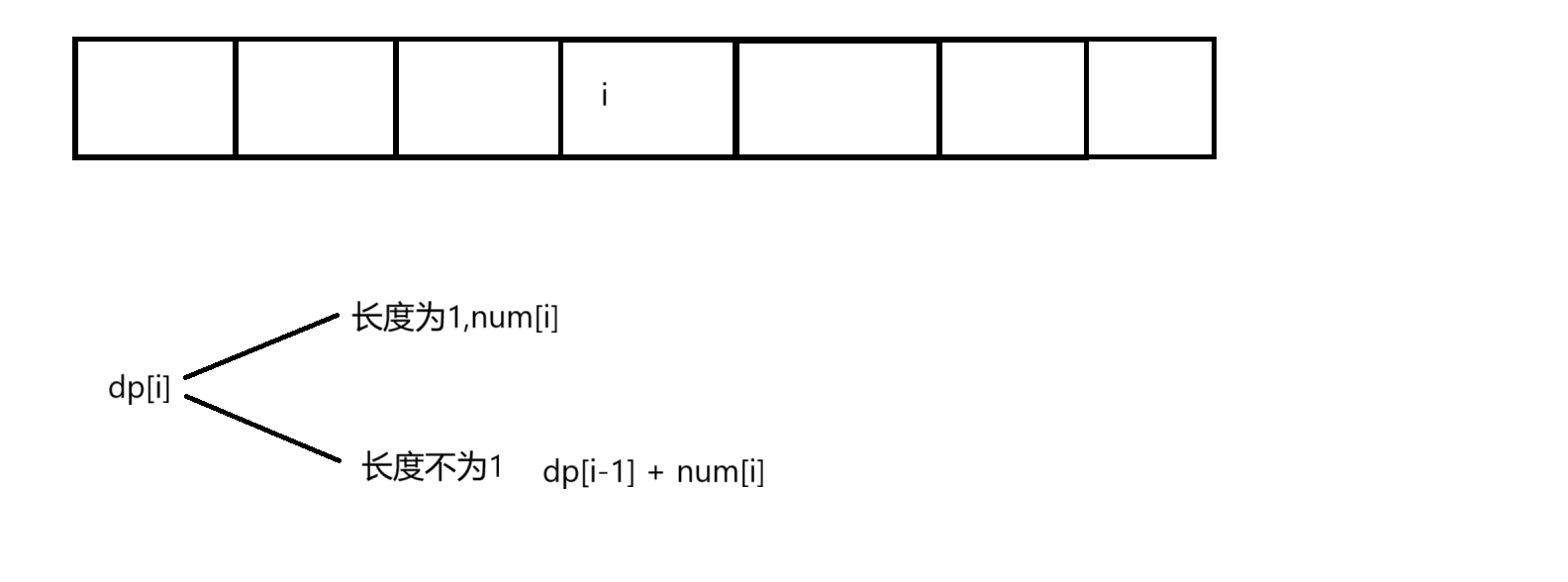
dp = max(num[i],dp[i-1] + num[i])

初始化

添加虚拟结点 dp[0] = 0；

填表顺序

从左到右

返回值

表中的最小值

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int maxSubArray(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int>dp(n+1);
        dp[0] = 0;
        int min = -0x3f3f3f;
        for(int i = 1; i<=n; i++)
        {
            dp[i] = max(nums[i-1],dp[i-1]+nums[i-1]);
            min = max(min,dp[i]);
        }
        return min;
    }
};

环形数组的最大和

https://leetcode.cn/problems/maximum-sum-circular-subarray/

（1）题目

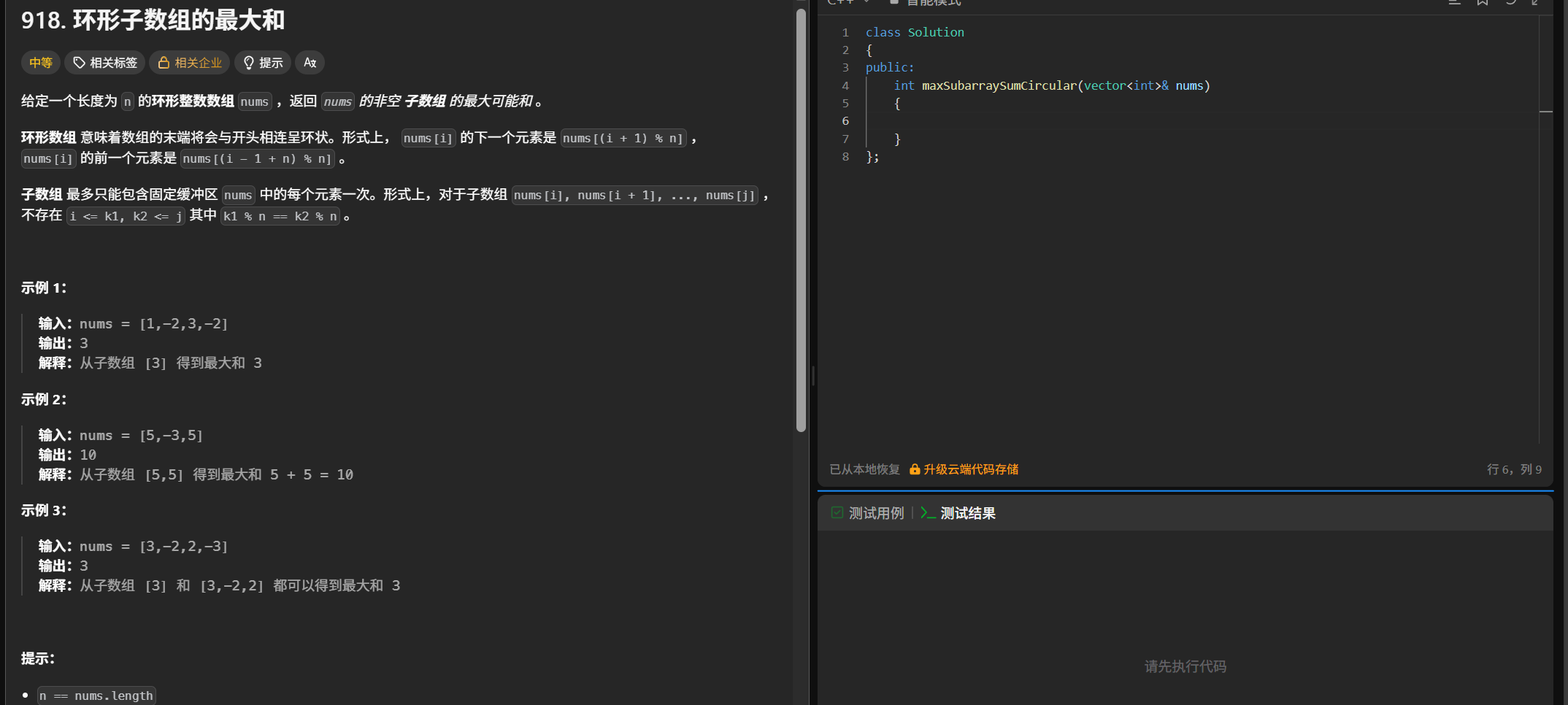
（2）解题思路

这道题和上一道题非常相似，最大子数组有两种情况，一种是向上面的一样最大子数组是连续的，一种是最后面一部分最前面一部分（这种情况我们可以转化为求中间的最小，然后将总数减去最小）

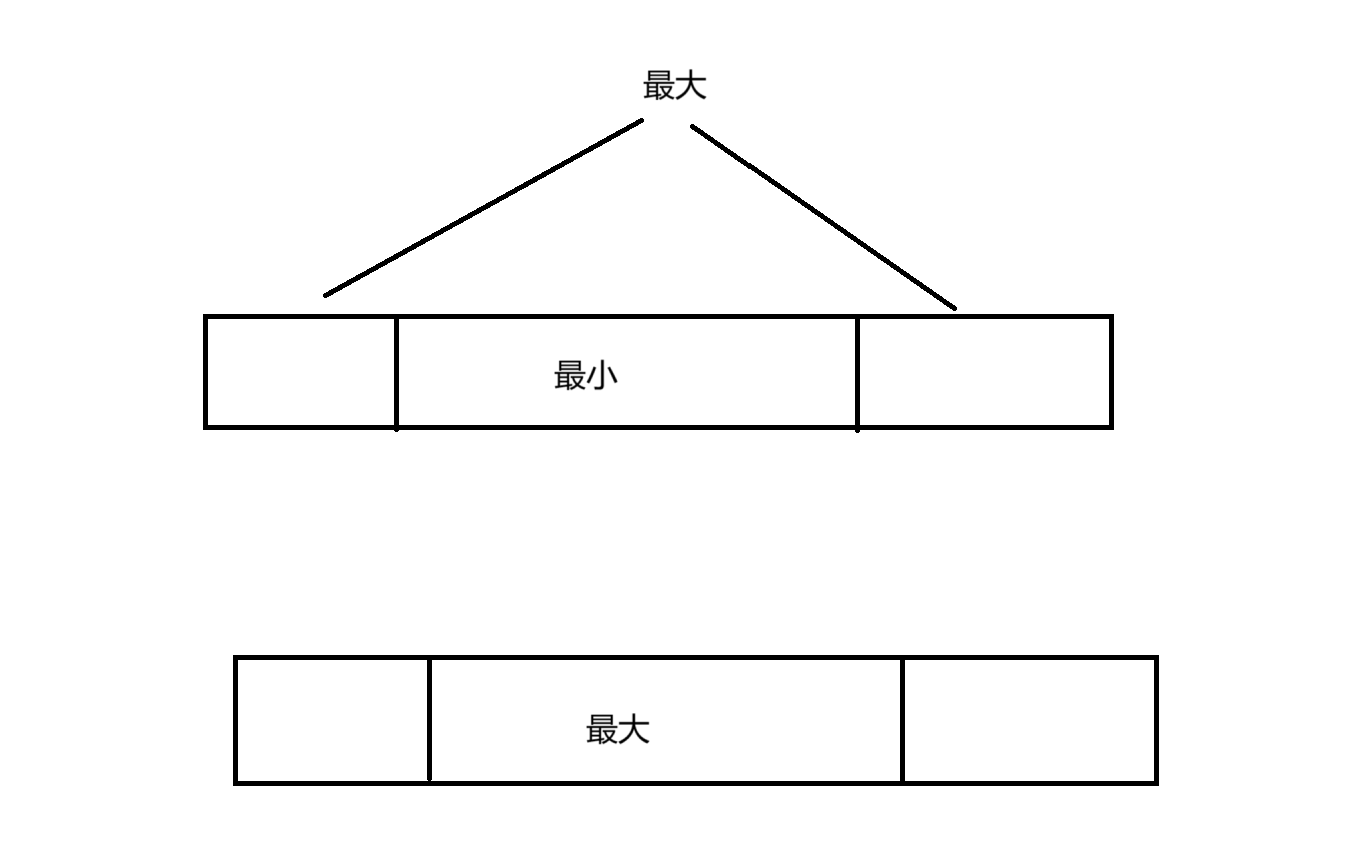
状态表示

f[i]: 表示以i为结尾所有子数组中最大和

g[i]:表示以i为结尾所有子数组中最大和

状态转移方程

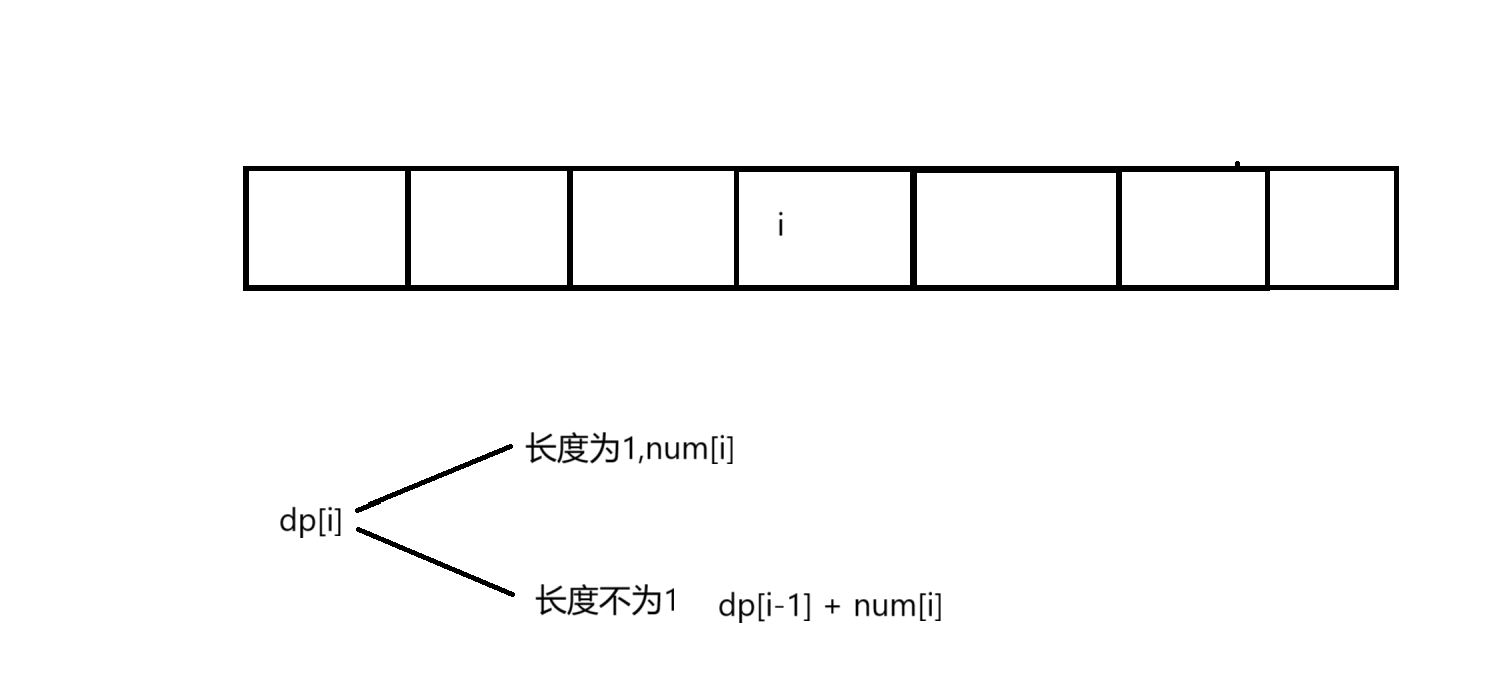
f[i] = max(num[i],f[i-1] + num[i])

g[i] = min(num[i],g[i-1]+ num[i])

初始化

虚拟节点

f[0] = g[0] = 0;

填表顺序

从左到右

返回值

max(f[i]中的最大值，总数-g[i]中最小值)

注意：如果sum = g[i] 那么它的意思全部为负数，全部不选是最大值，但是题目规定必须选，此时最大值为f[i]中的最大值

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int maxSubarraySumCircular(vector<int>& num) 
    {
        int n = num.size();
        vector<int> f(n+1);
        auto g = f;
        int _min = INT_MAX;
        int _max = INT_MIN;
        int sum = 0;
        for(int i = 1; i<=n; i++)
        {
           f[i] = max(num[i-1],f[i-1] + num[i-1]);
           g[i] = min(num[i-1],g[i-1]+ num[i-1]);
           sum+= num[i-1];
           _min = min(_min,g[i]);
           _max = max(_max,f[i]);
        }
        if(_min!=sum)
        {
            return max(sum-_min,_max);
        }
        return _max;
    }
};

最大子数组之和

https://leetcode.cn/problems/maximum-subarray/submissions/667609029/

（1）题目

（2）解题思路

状态表示

以i位置为结尾，dp[i]表示以i为结尾的子数组的最大和

状态转移方程

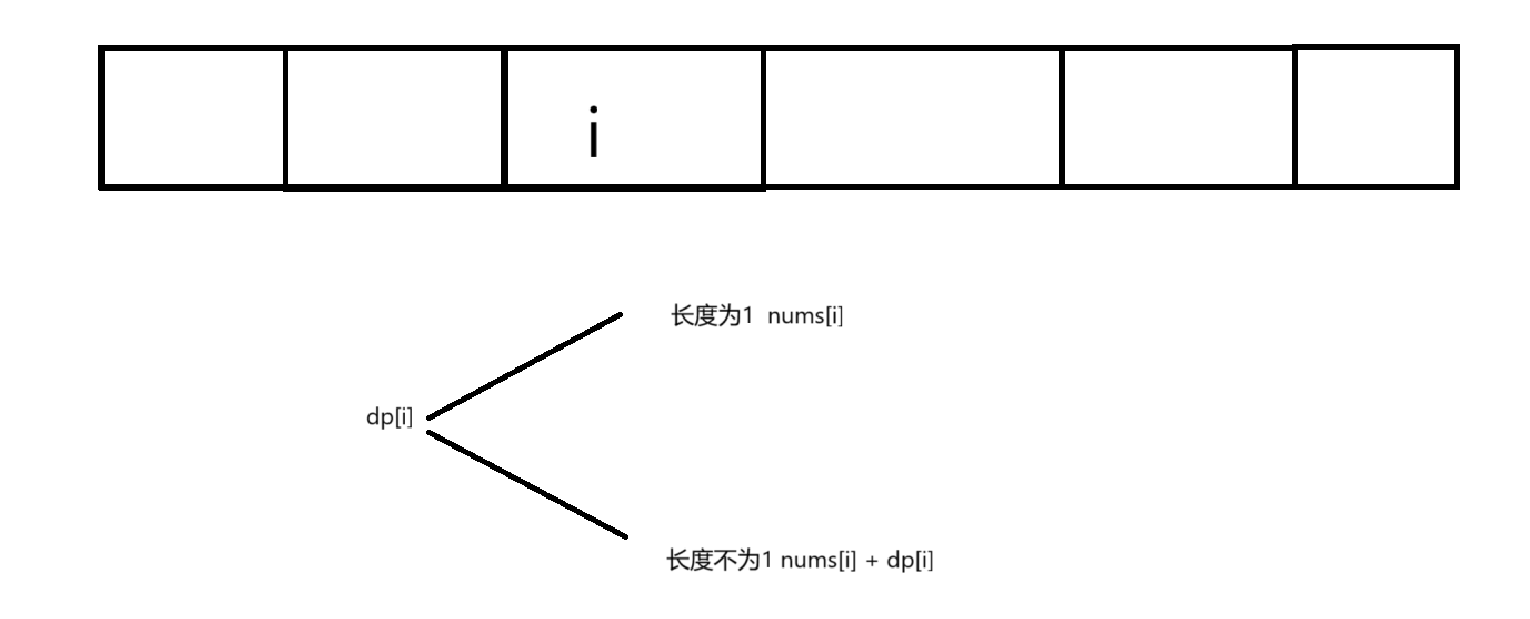
dp[i] = max(nums[i],nums[i]+dp[i])

初始化

使用虚拟节点，为满足 dp[1] = nums[0], dp[0]

填表顺序

从左到右

返回值

dp[i]中最大的一个

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int maxSubArray(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int>dp(n+1);
        dp[0] = 0;
        int min = -0x3f3f3f;
        for(int i = 1; i<=n; i++)
        {
            dp[i] = max(nums[i-1],dp[i-1]+nums[i-1]);
            min = max(min,dp[i]);
        }
        return min;
    }
};

乘积最大的子数组

https://leetcode.cn/problems/maximum-product-subarray/description/

（1）题目

（2）解题思路

状态表示

以i 为结尾 dp[i] 表示乘积最大的子数组，但是如果nums[i] 为负数需要dp[i-1]为最小值，反之需要最大值，所以需要两个状态表示

f[i] : 表示以i为结尾乘积最大的子数组

g[i]: 表示以i为结尾乘积最小的子数组

状态转移方程

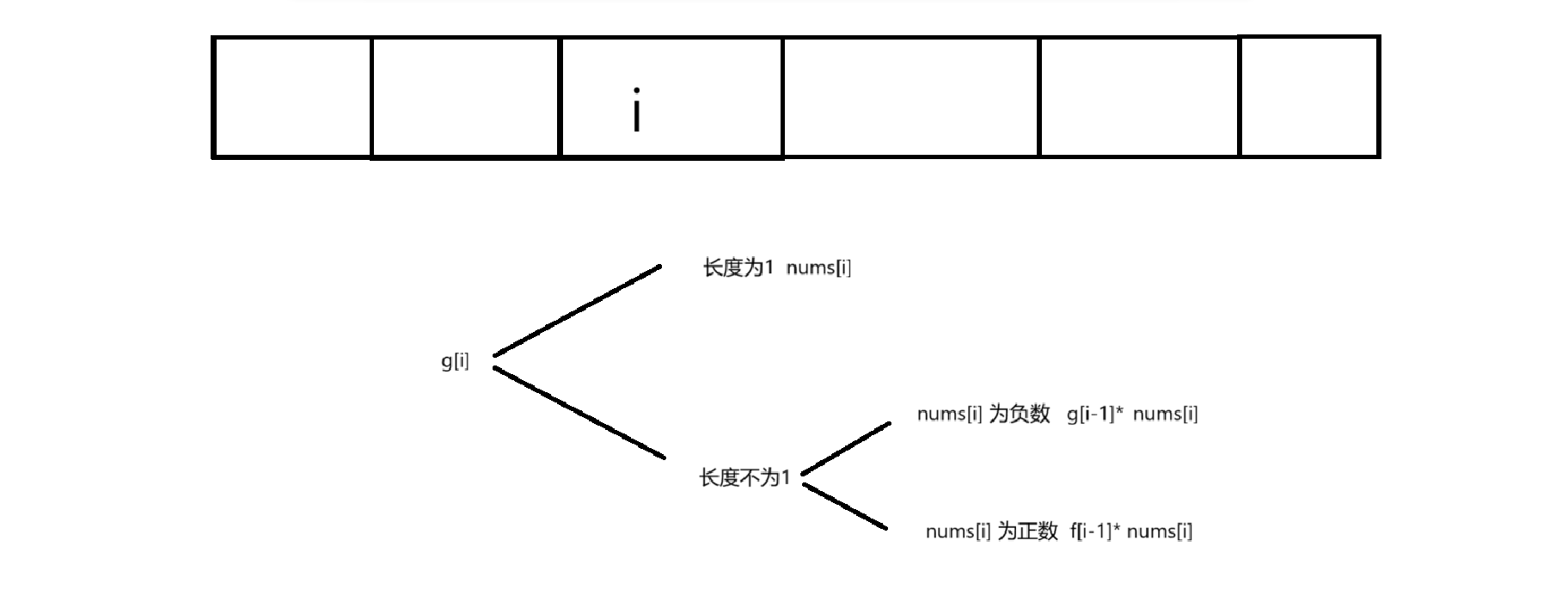
f[i] = max(nums[i] , g[i-1]*nums[i], f[i-1]*nums[i])

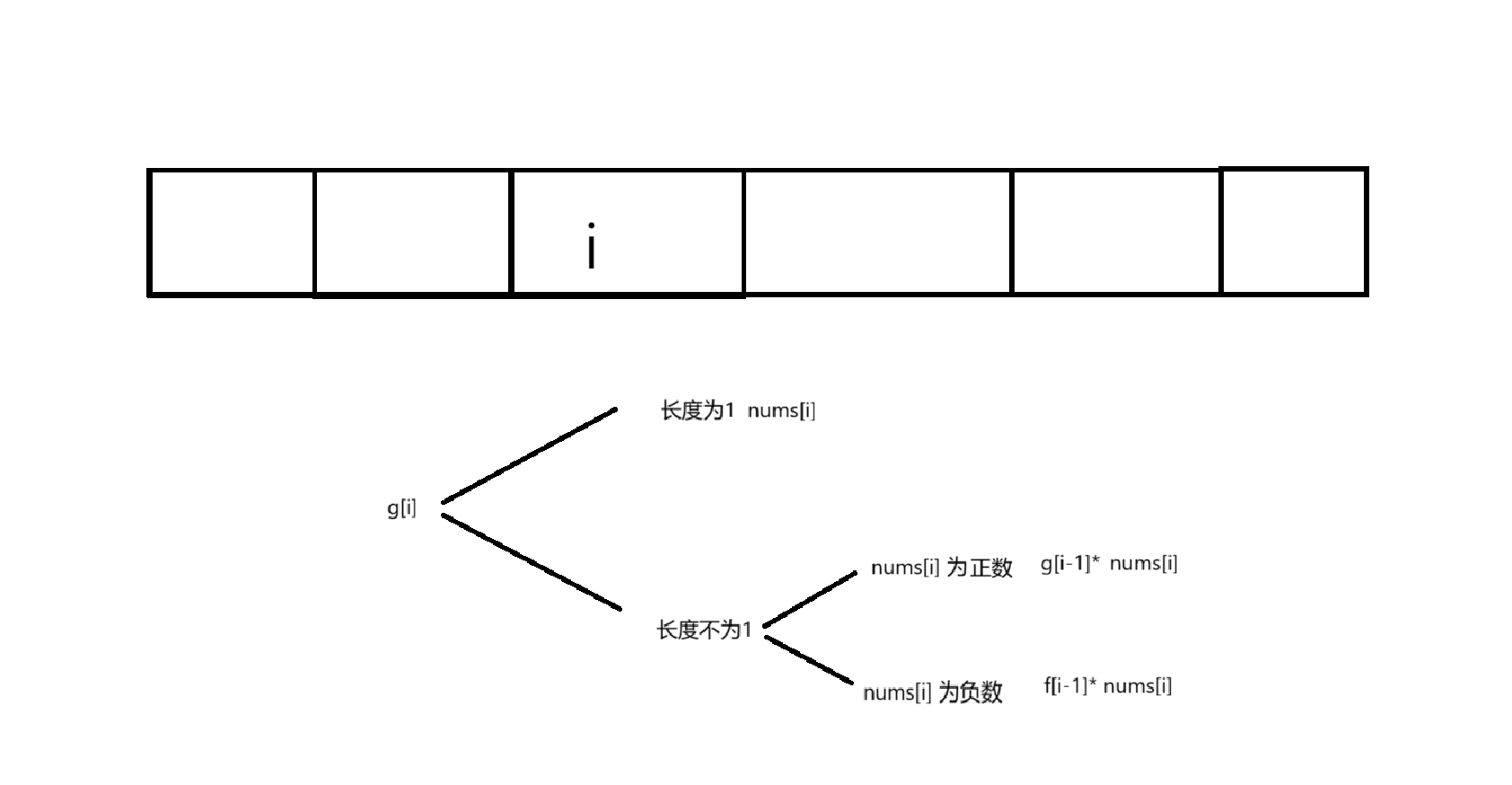
g[i] = min(nums[i] , g[i-1]*nums[i], f[i-1]*nums[i])

初始化

虚拟节点

为了保证f[1]= g[1] = nums[0]， g[0] = f[0] = 1;

返回值

g[i]中的最大值

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int maxProduct(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n+1);
        auto g = f;
        g[0] = f[0] = 1;
        int rmax = -0x3f3f3f;
        for(int i = 1; i<=n; i++)
        {
            int x = nums[i-1];
            int y = x * f[i-1];
            int z = x * g[i-1];
            f[i] = max(x,max(y,z));
            g[i] = min(x,min(y,z));
            rmax = max(rmax,f[i]);
        }
        return rmax;
    }
};

乘积为正整数的最长子数组之和

https://leetcode.cn/problems/maximum-length-of-subarray-with-positive-product/description/

（1）题目

（2）解题思路

状态表示

以i为结尾 dp[i]表示以i 为结尾乘积为正数的最长子数组长度，numd[i]分为正数和负数，所以我们有两种状态

f[i] : 表示以i为乘积为正数的最长子数组长度

g[i]：表示以i为乘积为负数的最长子数组长度

状态转移方程

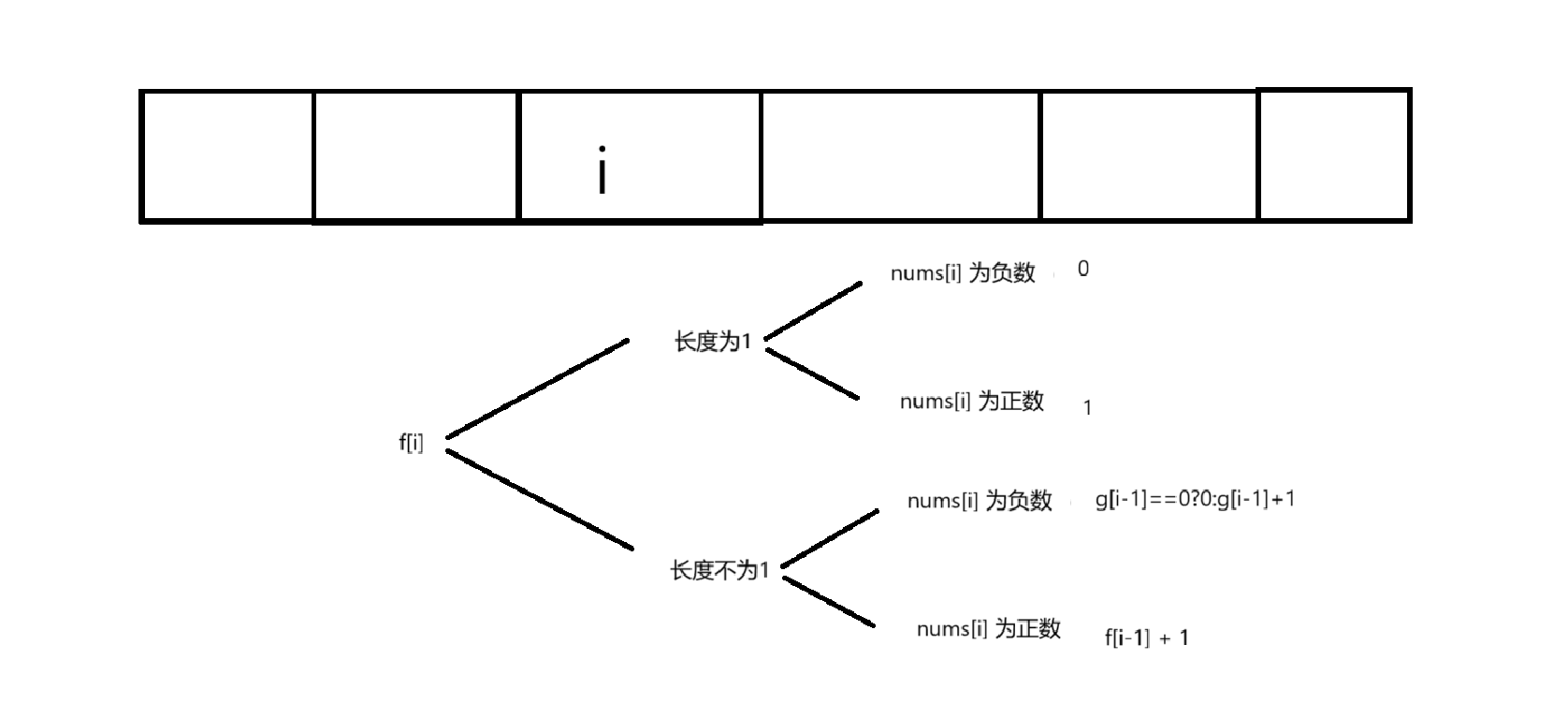
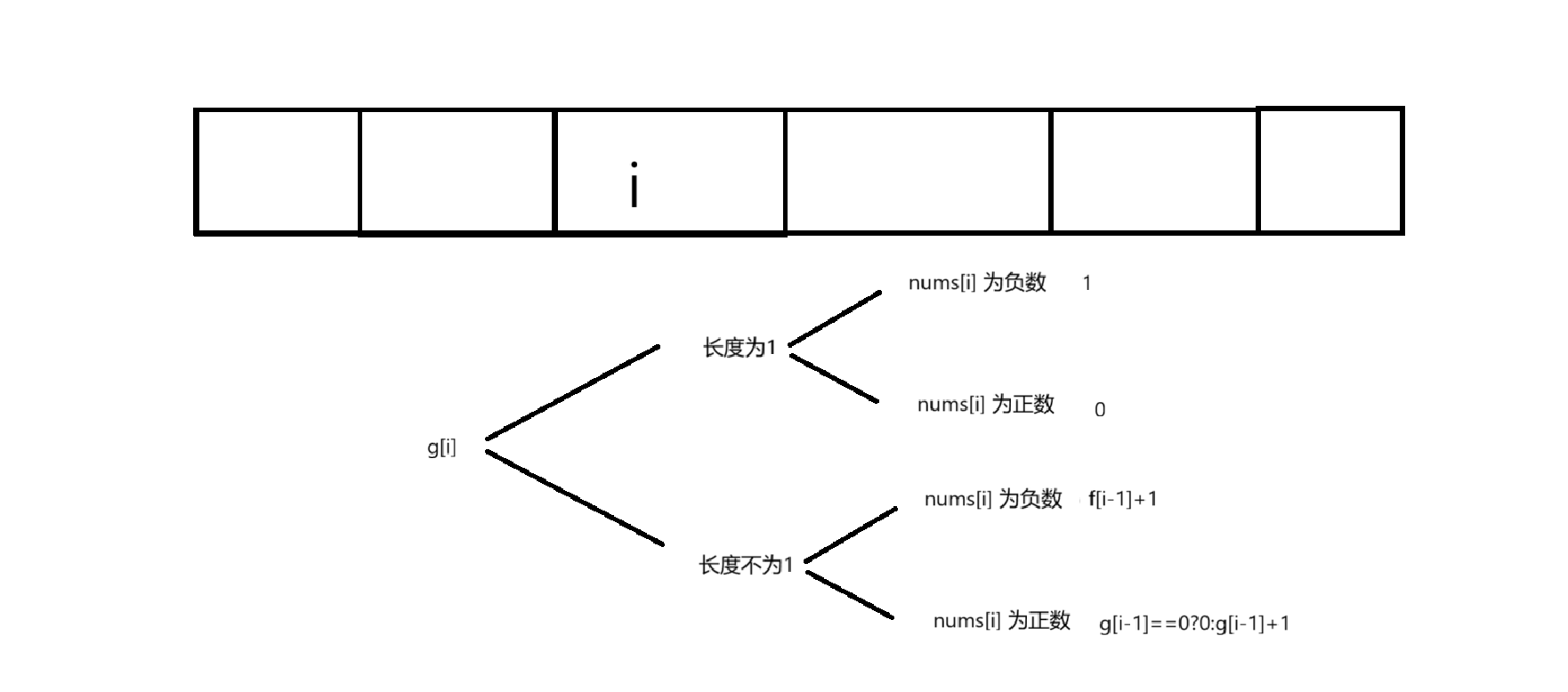
初始化

虚拟节点

f[0] = g[0] = 0

填表顺序

从左到右，两个表一起填

返回值

f[i]中的最大值

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int getMaxLen(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n+1);
        auto  g = f;
        int rmax = -0x3f3f3f;
        for(int i = 1; i<=n; i++)
        {
            if(nums[i-1]>0)
            {
                f[i] = f[i-1]+1;
                g[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
            }
            else if(nums[i-1]<0)
            {
                f[i] = g[i-1] == 0 ? 0 : g[i-1] + 1;
                g[i] = f[i-1]+1;
            }
            rmax = max(rmax,f[i]);
        }
        return rmax;
    }
};

等差数组的划分

https://leetcode.cn/problems/arithmetic-slices/description/

（1）题目

（2）解题思路

状态标识

以i为结尾，dp[i]表示以i为结尾的等差数列的个数

状态转移方程

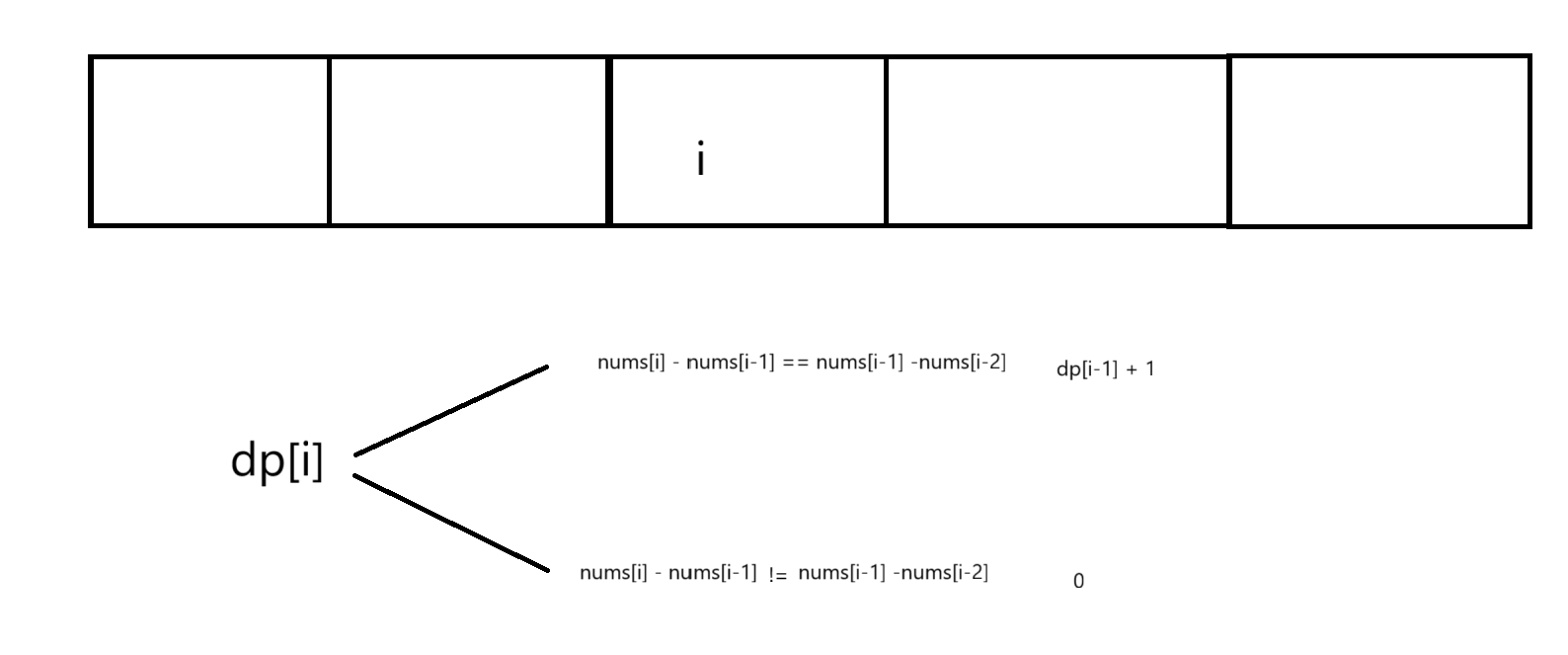
初始化

dp[0] = dp[1] = 0

填表顺序

从左到右

返回值

所有dp[i]相加

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int numberOfArithmeticSlices(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> dp(n);
        int sum =0;
        for(int i = 2; i<n; i++)
        {
            int x = nums[i-2];
            int y = nums[i-1];
            int z = nums[i];
            dp[i] = z-y == y-x ? dp[i-1] + 1 : 0;
            sum += dp[i];
        }
        return sum;
    }
};

最长湍流子数组

https://leetcode.cn/problems/longest-turbulent-subarray/description/

（1）题目

（2）解题思路

状态表示

以i为结尾dp[i]表示以为结尾最长的湍流子数组

i 有两种情况，上升状态，下降状态

f[i]表示以i为结尾时，上升状态的最大湍流子数组个数

g[i]表示以i为结尾时，上升状态的最大湍流子数组个数

状态转移方程

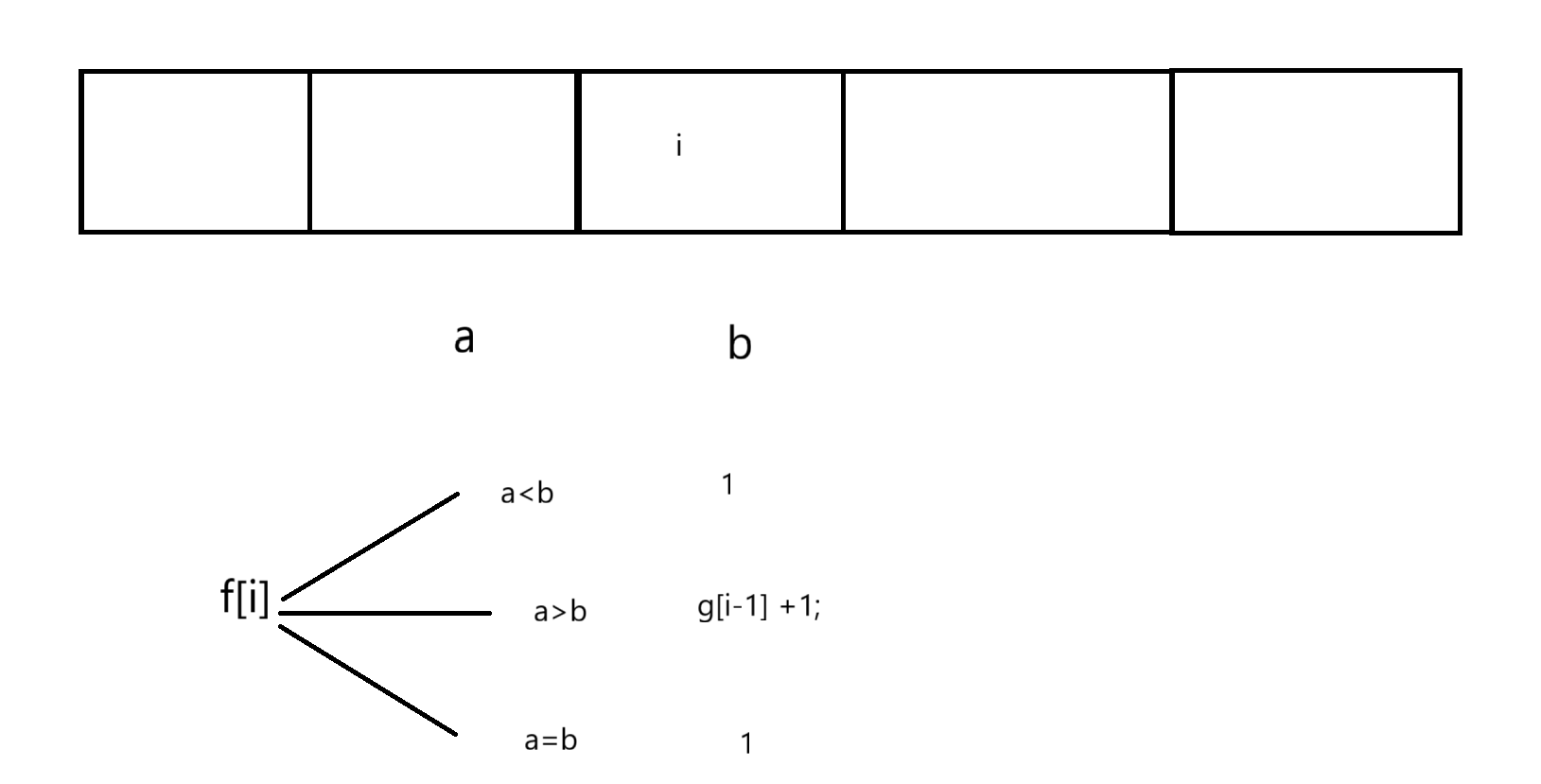
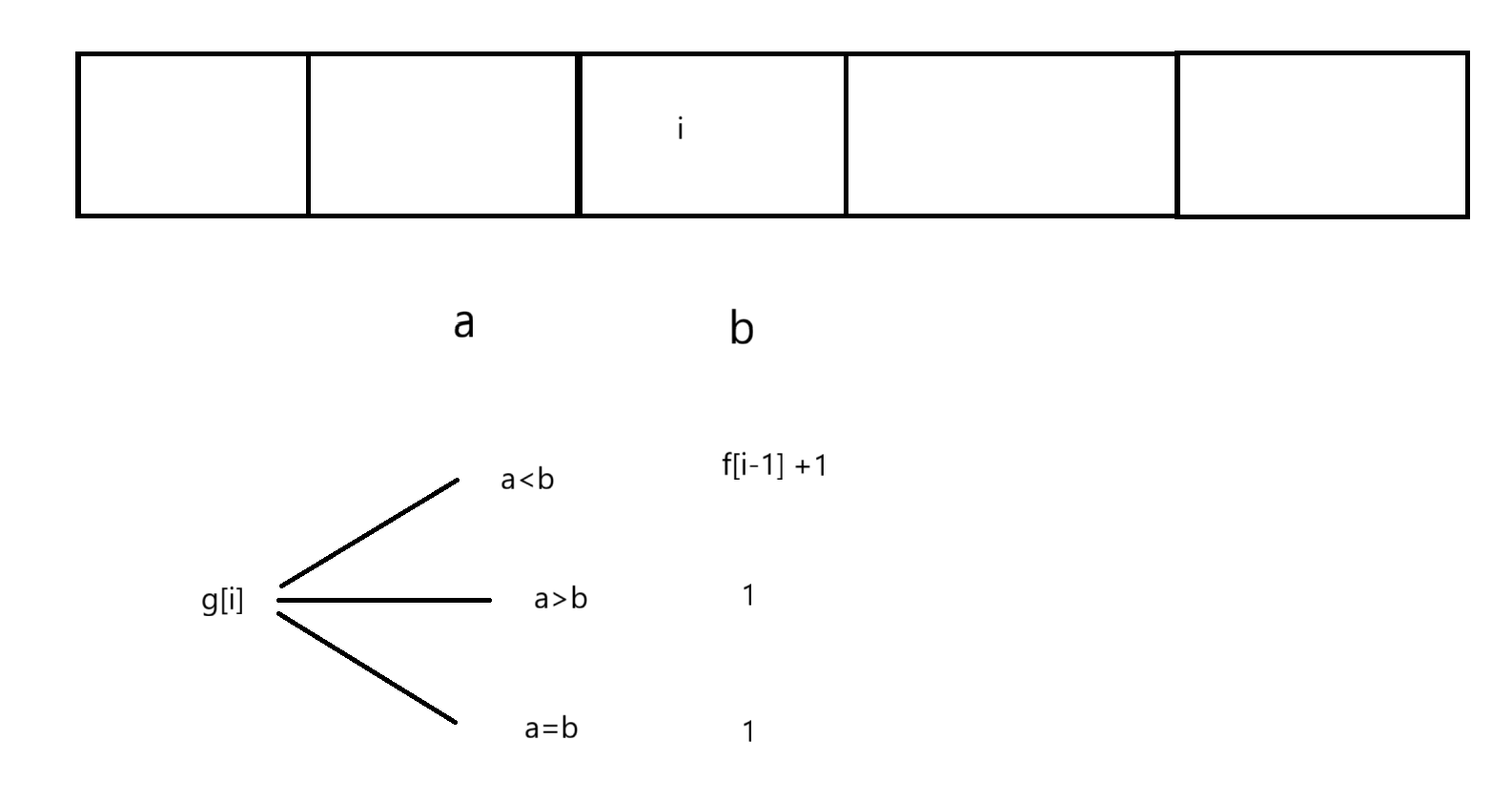
初始化

f[0] = g[0] = 1，我们发现很多情况都是为1所以我们可以将整个数组最开始都初始化为1

填表顺序

从左到右，两个一起填

返回值

f[i]和g[i]中的最大值

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int maxTurbulenceSize(vector<int>& nums) 
    {
        
        int n = nums.size();
        if(n<2)
        {
            return 1;
        }
        vector<int> f(n,1);
        auto g = f;
        int rmax = INT_MIN;
        for(int i = 1; i<n; i++)
        {
            int a = nums[i-1];
            int b = nums[i];
            if(a>b)
            {
                g[i] = f[i-1] + 1;
            }
            else if(a<b)
            {
                f[i] = g[i-1] + 1;
            }
            rmax = max(rmax,max(g[i],f[i]));
        }
        return rmax;
    }
};

单词划分

https://leetcode.cn/problems/word-break/description/

（1）题目

（2）解题思路

状态表示

以i为结尾 dp[i]表示[0,i]区间的字符串，能否被字典的单词拼接而成

状态转移方程

根据最后一个位置，来划分问题

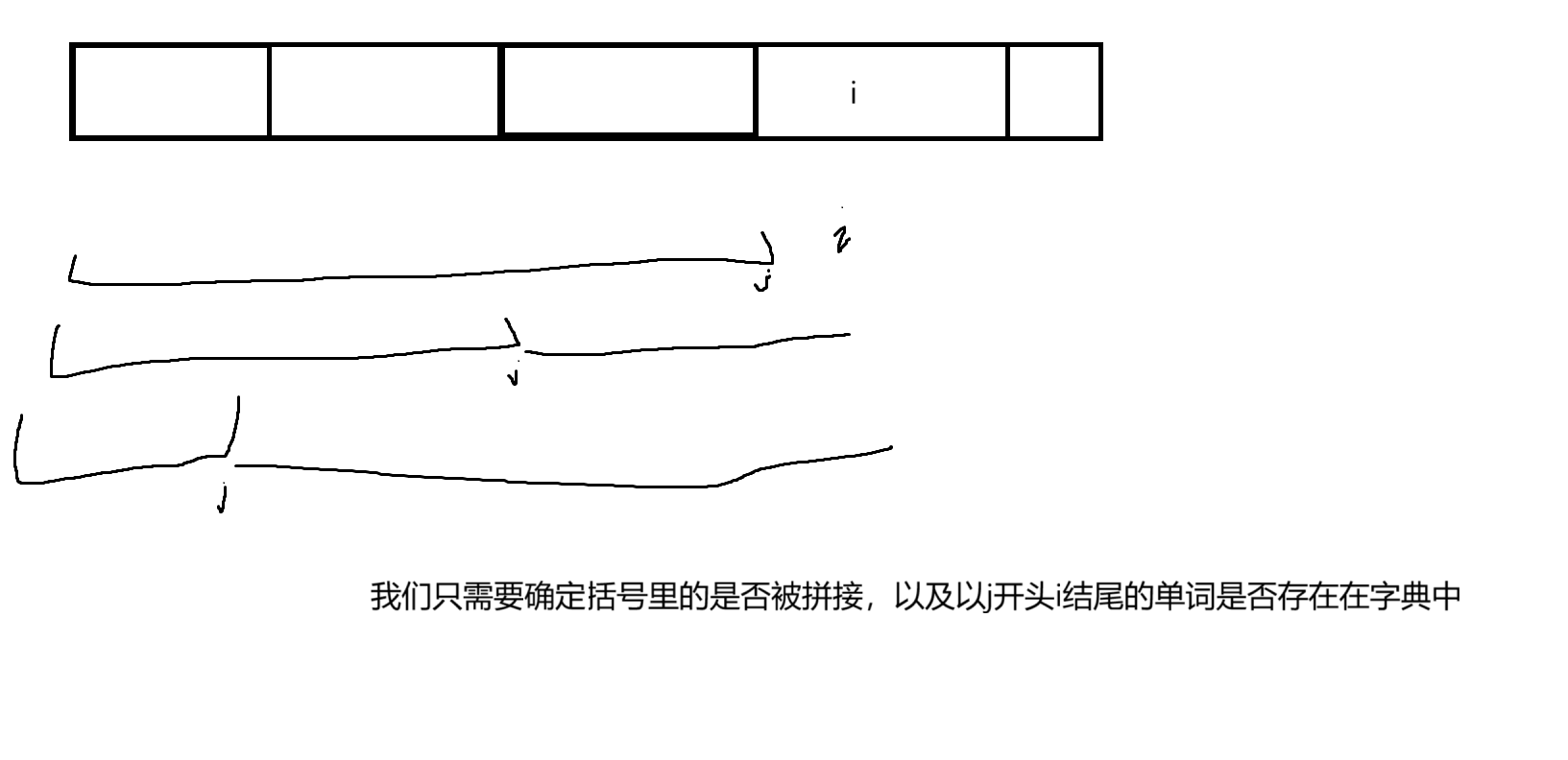
初始化

虚拟节点

dp[0] = true;

我们可以将字符串多添加一个，这样就不用考虑映射关系

填表顺序

从左到右

返回值

dp[n]

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    bool wordBreak(string s, vector<string>& wordDict) 
    {
        unordered_set<string> hash;
        for(auto e: wordDict) hash.insert(e);
        int n = s.size();
        vector<int> dp(n+1);
        dp[0] = true;
        s = ' ' + s;
        for(int i = 1; i<=n;i++)
        {
            for(int j = i; j>=1; j--)
            {
                if(dp[j-1 ]&& hash.count(s.substr(j,i-j+1)))
                {
                    dp[i] = true;
                    break;
                }
                else
                {
                    dp[i] = false;
                }
            }
        }
        return dp[n];
    }
};

环绕字符串中唯一的字符串

https://leetcode.cn/problems/unique-substrings-in-wraparound-string/description/

（1）题目

（2）解题思路

状态表示

以i 为结尾， dp[i]表示以i为结尾的子字符串的个数

状态转移方程

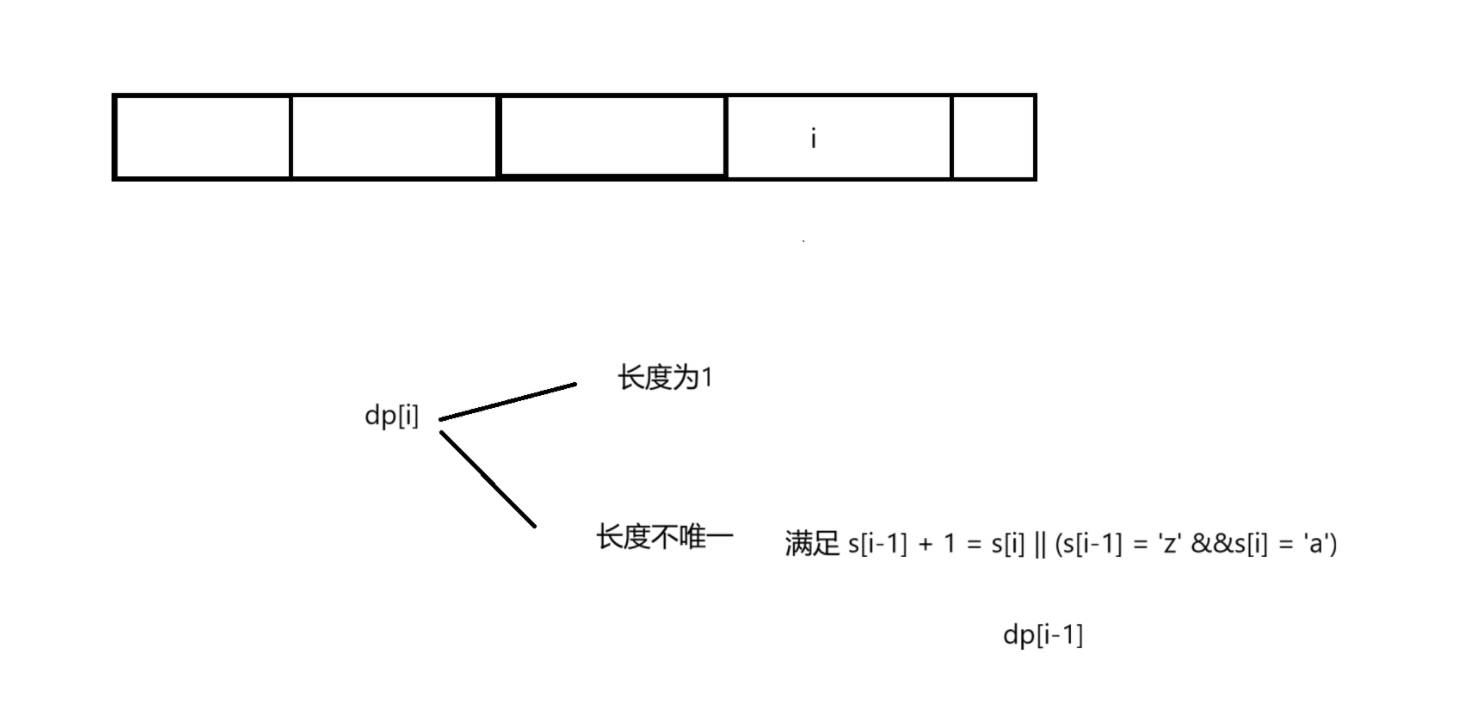
初始化

如果我们首先全部初始化为1 将不需要考虑很多，且dp[i] 变成了dp[i] += d[i-1];

填表顺序

从左到右

返回值

本题中我们同一个数结尾的取最大的值，防止重复

（3）代码实现

cpp 复制代码

class Solution
{
public:
    int findSubstringInWraproundString(string s) 
    {
        int n = s.size();
        vector<int> dp(n,1);
        for(int i = 1;i < n; i++)
        {
            if(s[i-1]+1==s[i]||(s[i-1])== 'z' && s[i] == 'a')
            {
                dp[i] += dp[i-1];
            }
        }
        int hash[26];
        for(int i = 0; i < n; i++)
        {
            hash[s[i]-'a'] = max(dp[i],hash[s[i]-'a']);
        }
        int sum = 0;
        for(auto e: hash)
        {
            sum+= e;
        }
        return sum;
    }
};

最大子数组之和

https://leetcode.cn/problems/longest-increasing-subsequence/

（1）题目

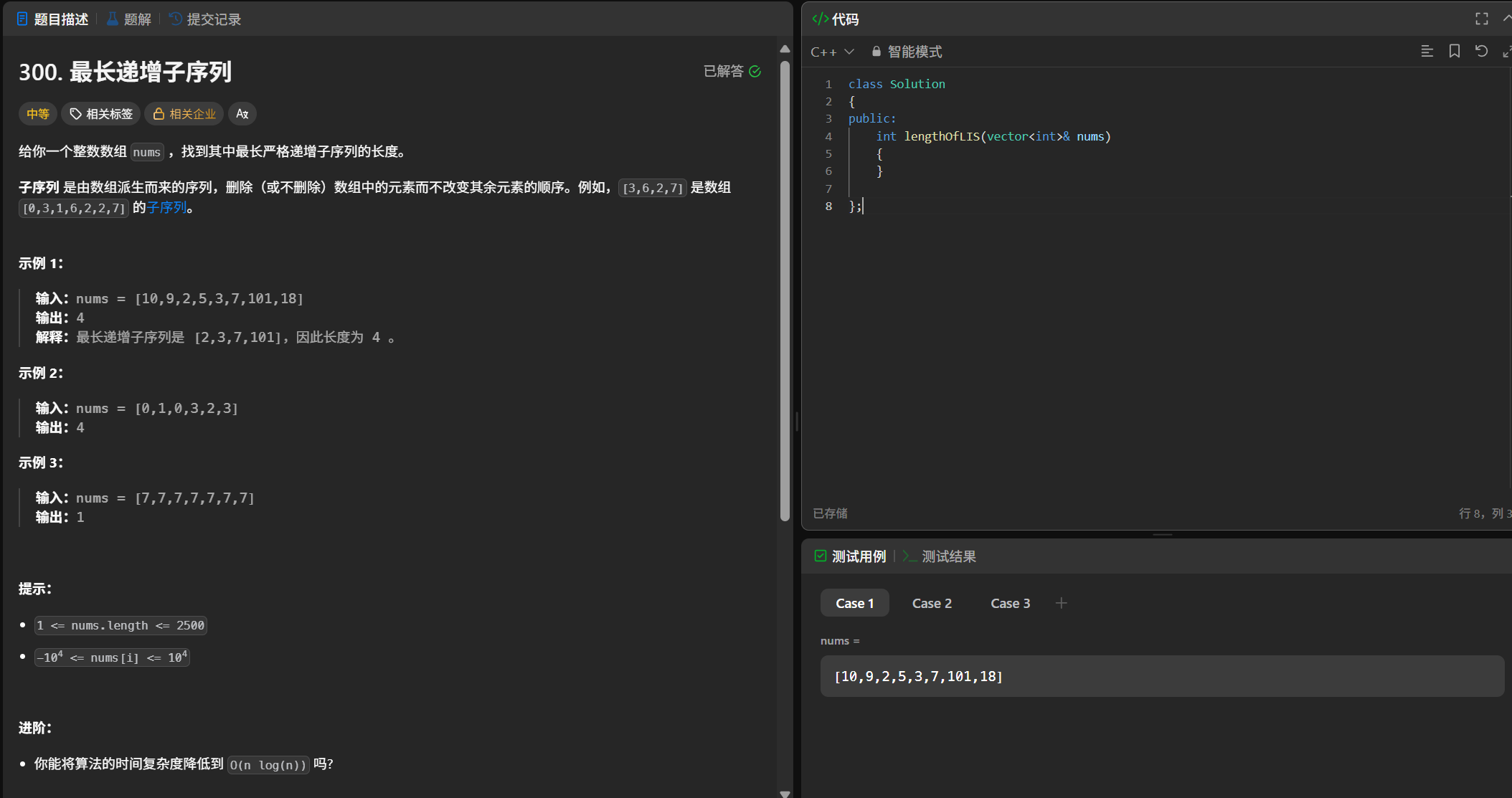
（2）解题思路

状态标识

以i为结尾，dp[i]标识以i为结尾的最长递增子序列的长度

状态转移方程

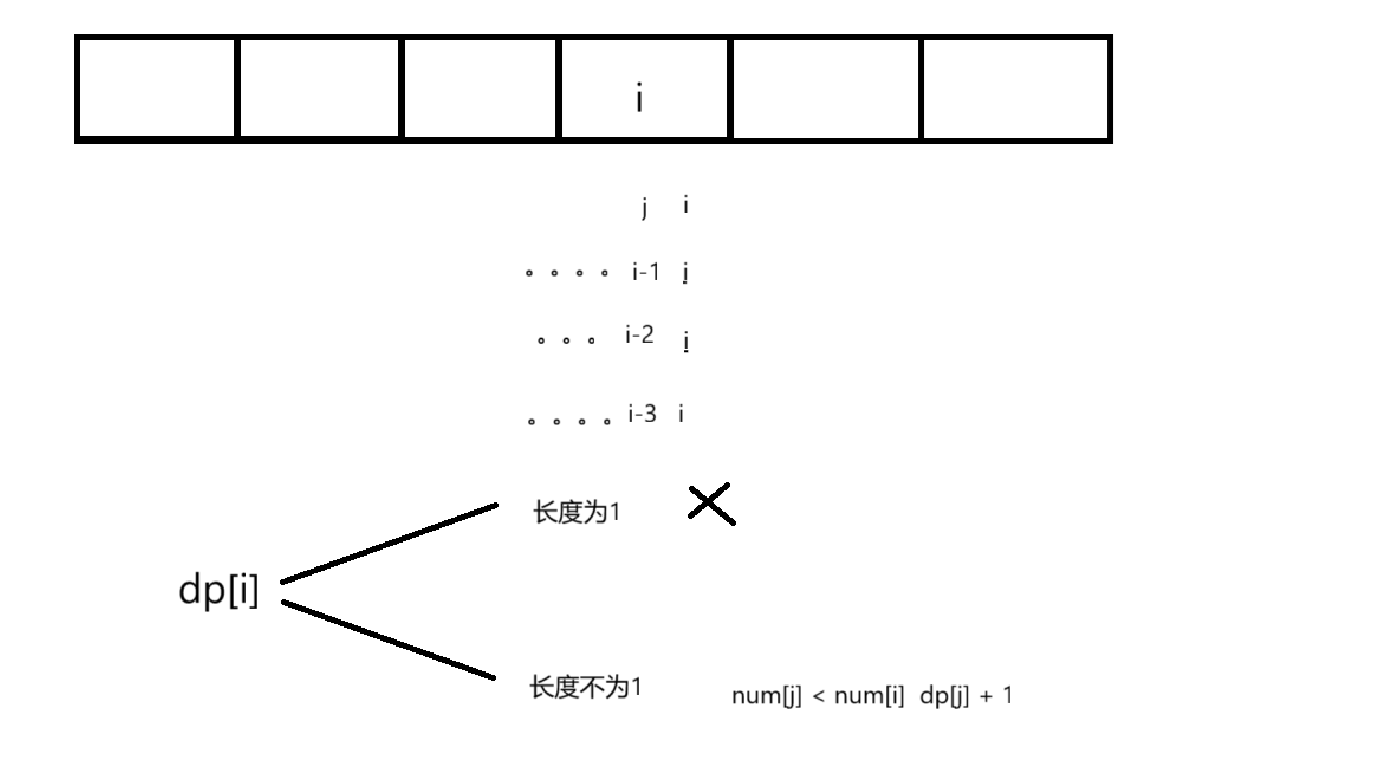
初始化

表里的所有都初始化为1

返回值

dp表中的最大值

（3）代码书写

cpp 复制代码

class Solution 
{
public:
    int lengthOfLIS(vector<int>& nums) 
    {

        int n = nums.size();
        vector<int> dp(n,1);
        int sum = 1;
        for(int i = 1; i<n; i++)
        {
            for(int j = 0; j<i; j++)
            {
                if(nums[j] < nums[i])
                dp[i] = max(dp[i],dp[j]+1);
            }
            sum = max(sum,dp[i]);
        }
        return sum;
    }
  
};

摆动序列

https://leetcode.cn/problems/wiggle-subsequence/description/

（1）题目

（2）解题思路

状态表示

以i为结尾， dp[i]表示以 i位置为结尾的所有的子序列，最长的摆动序列的长度

在i位置有两个状态上升和下降

f[i]: i位置为结尾的所有的子序列，最后一个位置呈现上升趋势，最长的摆动序列的长度

g[i]: i位置为结尾的所有的子序列，最后一个位置呈现下降趋势，最长的摆动序列的长度

状态转移方程

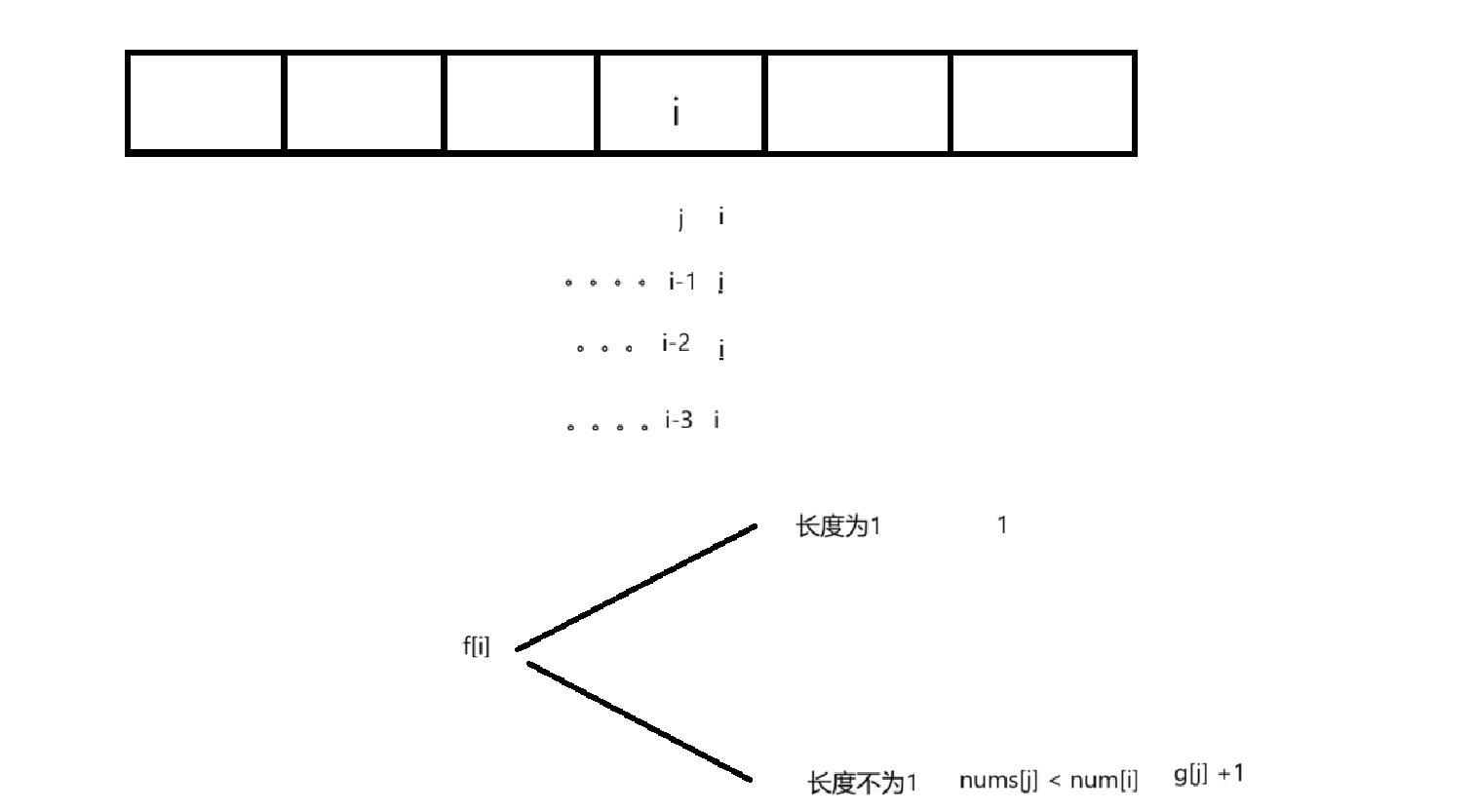
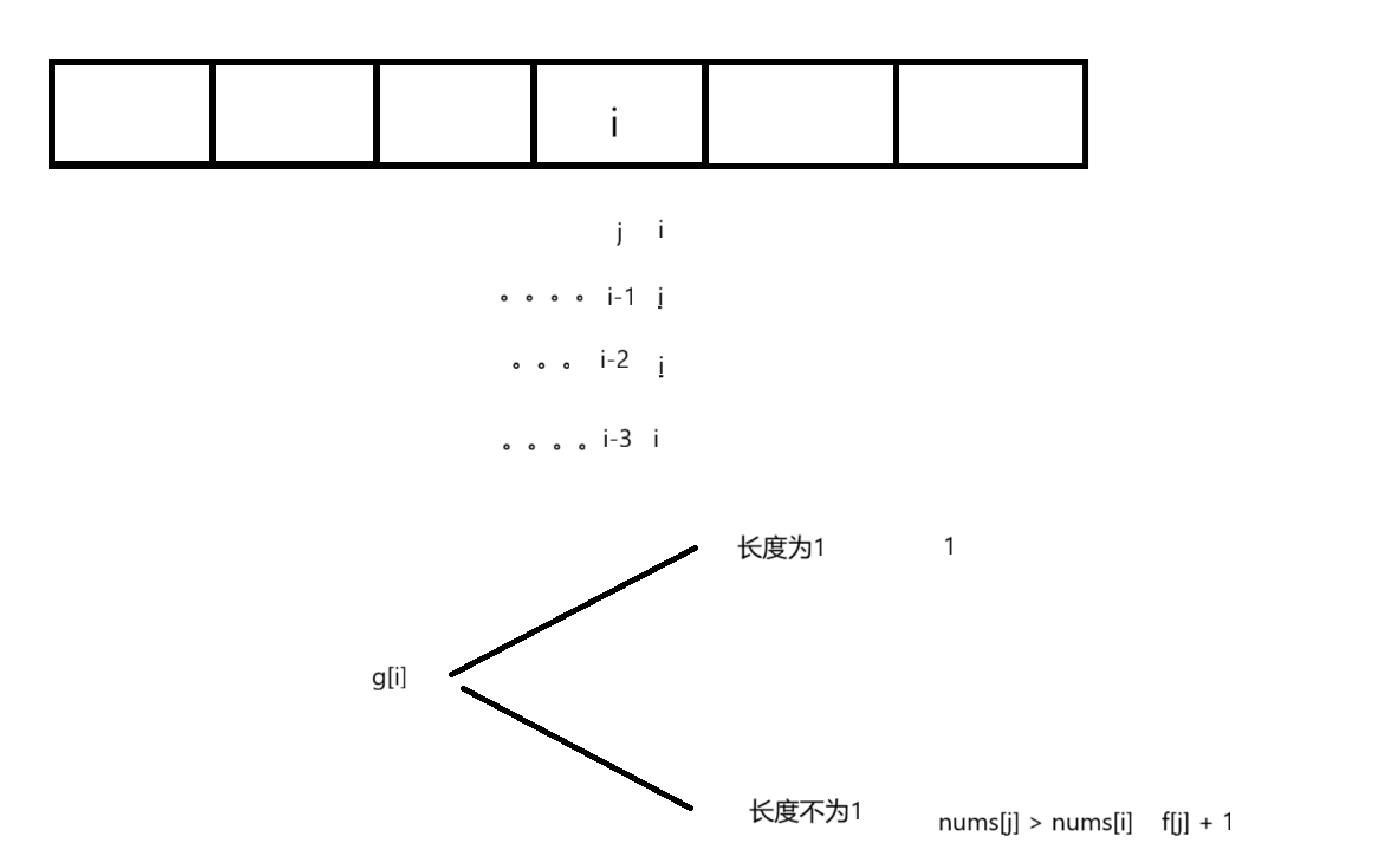
初始化

f表和g表全部初始化为1

填表顺序

从左到右，两个表一起填

返回值

两个表的最大值

（3）代码实现

cpp 复制代码

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> f(n,1);
        auto g = f;
        int sum = 1;
        for(int i = 1; i<n; i++)
        {
            for(int j = 0; j<i; j++)
            {
                if(nums[j] < nums[i]) f[i] = max(f[i], g[j]+1);
                else if(nums[j] > nums[i]) g[i] = max(g[i], f[j]+1);
            }
            sum = max(sum,max(f[i],g[i]));
        }
        return sum;
    }
};

最长递增子序列的个数

https://leetcode.cn/problems/number-of-longest-increasing-subsequence/description/

（1）题目

（2）解题思路

前置思想

一个数组，我们可以通过一次遍历，找出他的最大数的个数

状态标识

以i为结尾，dp[i]表示以i为结尾最长递增子序列的个数

因为我们需要知道以i为结尾的最长递增子序列，所以我们需要两个状态表示

len[i] : 以i位置为结尾的所有的子序列中，最长递增子序列的长度

count[i]: 以i位置为结尾的所有的子序列中，最长递增子序列的"个数"

状态转移方程

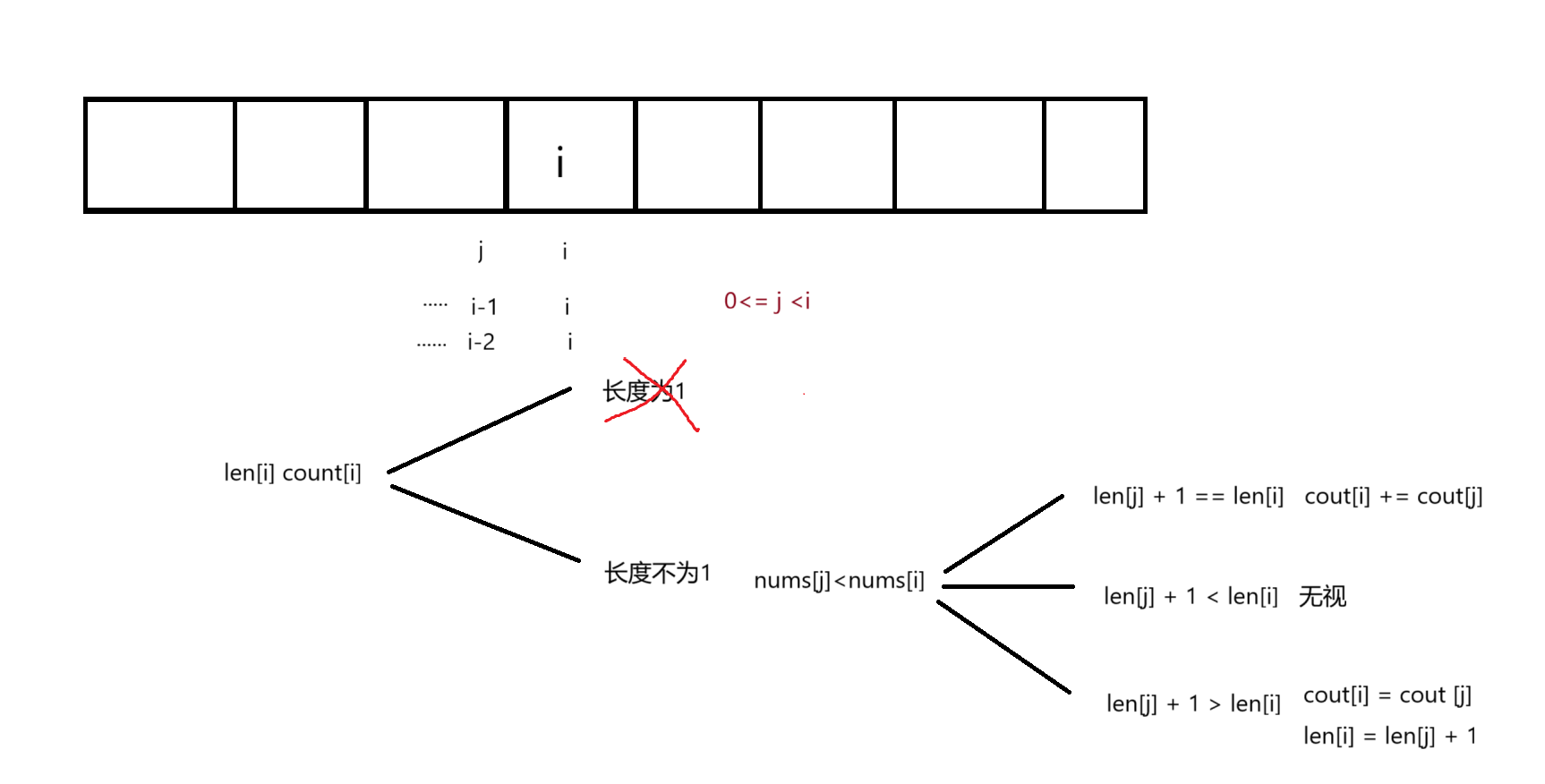
初始化

全部初始化为1

填表顺序

从左到右

返回值

上述思想找到最大长长度的最大值

（3）代码实现

cpp 复制代码

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int> len(n,1);
        auto count = len;
        int rlen = 1;
        int rcout = 1;
        for(int i = 1; i<n; i++)
        {
            for(int j = 0; j < i; j++)
            {
                if(nums[j] < nums[i])
                {
                    if(len[j]+1 == len[i])
                    {
                        count[i] += count[j];
                    }
                    else if(len[j]+1>len[i])
                    {
                        len[i] = len[j] + 1;
                        count[i] = count[j];
                    }
                }
            }
            if(len[i]>rlen)
            {
                rcout = count[i];
                rlen = len[i];
            }
            else if(len[i] == rlen)
            {
                rcout += count[i];
            }
        }
        return rcout;
    }
};

最长数对链

https://leetcode.cn/problems/maximum-length-of-pair-chain/description/

（1）题目

（2）解题思路

前置思路：我们需要先将他们进行排序，确保可以按照顺序拿取，可以使用动态规划

状态标识

以i 为结尾 dp[i]表示以i位置为结尾的最长数对链

状态转移方程

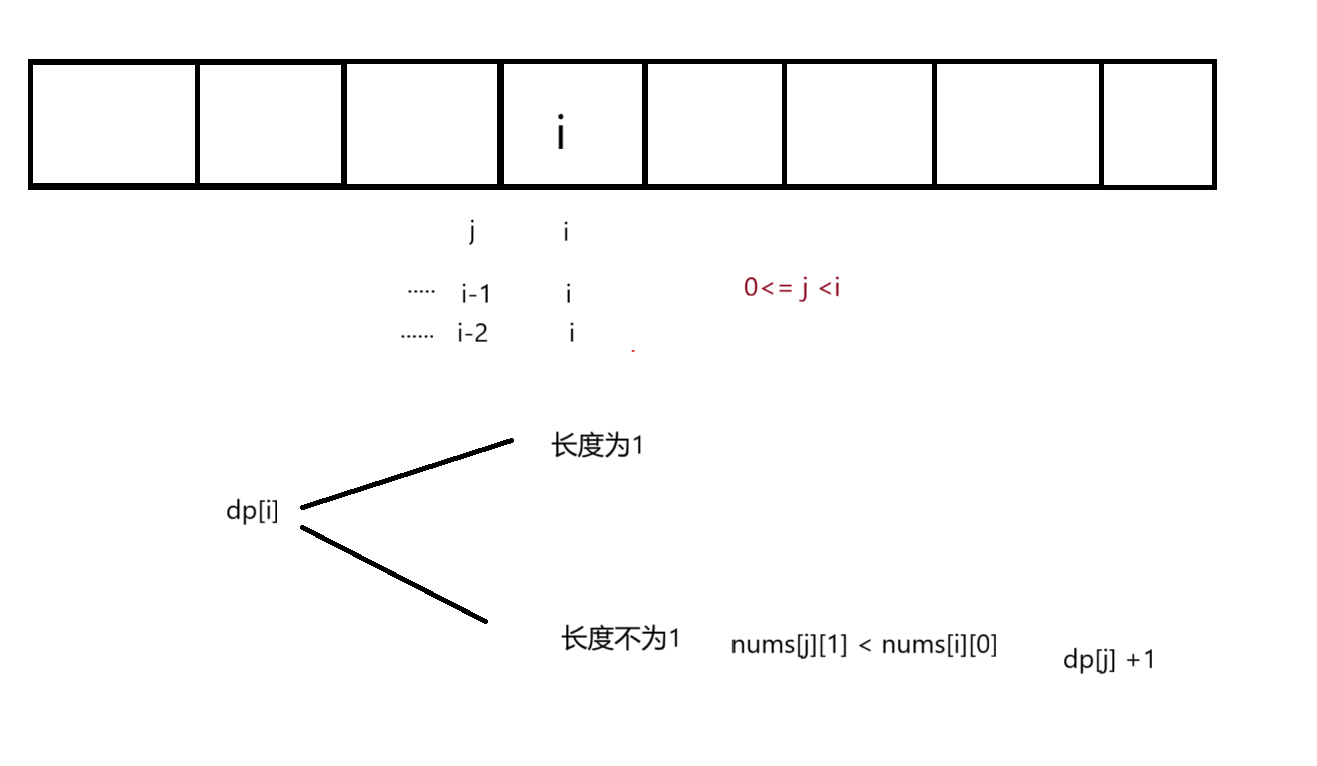
初始化

全部初始化为1

填表顺序

从左到右

返回值

dp[i]的最大值

（3）代码实现

cpp 复制代码

class Solution {
public:
    int findLongestChain(vector<vector<int>>& pairs) 
    {
        sort(pairs.begin(),pairs.end());
        int n = pairs.size();
        int sum = 1;
        vector<int> dp(n,1);
        for(int i = 1; i<n; i++)
        {
            for(int j = 0; j<i; j++)
            {
                if(pairs[j][1]<pairs[i][0])
                {
                    dp[i] = max(dp[j] + 1,dp[i]);
                }
            }
           sum = max(sum,dp[i]);
        }
        return sum;
    }
};

最长定差子序列

https://leetcode.cn/problems/longest-arithmetic-subsequence-of-given-difference/description/

（1）题目

（2）解题思路

状态表示

以i为结尾，dp[i]表示以i为最后一个位置最长的定差子序列的长度

状态表示

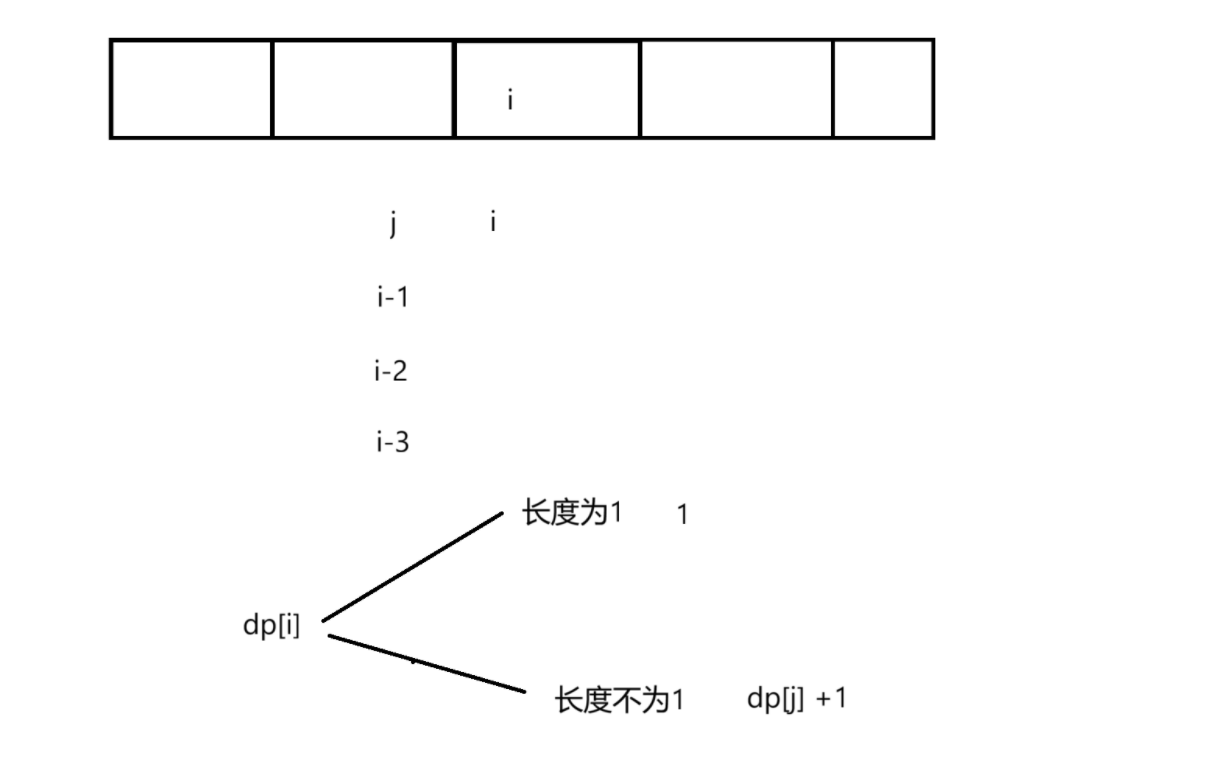
初始化

初始化为1

填表顺序

从左到右

返回值

dp[n]中最大的

（3）代码实现

cpp 复制代码

class Solution 
{
public:
    int longestSubsequence(vector<int>& arr, int difference) 
    {
        int n = arr.size();
        vector<int> dp(n,1);
        int sum = 1;
        for(int i = 1; i<n; i++)
        {
            for(int j = 0; j<i; j++)
            {
                if(arr[i]- arr[j] == difference)
                {
                    dp[i] = max( dp[j] + 1, dp[i]);
                }
            }
            sum = max(sum,dp[i]);
        }
        return sum;
    }
};

（4）优化

将他和哈希表绑定

cpp 复制代码

class Solution 
{
public:
    int longestSubsequence(vector<int>& arr, int difference) 
    {
        int n = arr.size();
        unordered_map<int ,int> hash;
        hash[arr[0]] = 1;
        int sum = 1;
        for(int i = 1; i<n; i++)
        {
            hash[arr[i]] = hash[arr[i]-difference] +1;
            sum = max(hash[arr[i]],sum);
        }
        return sum;
    }
};

最长的菲波那契子序列的长度

https://leetcode.cn/problems/length-of-longest-fibonacci-subsequence/

（1）题目

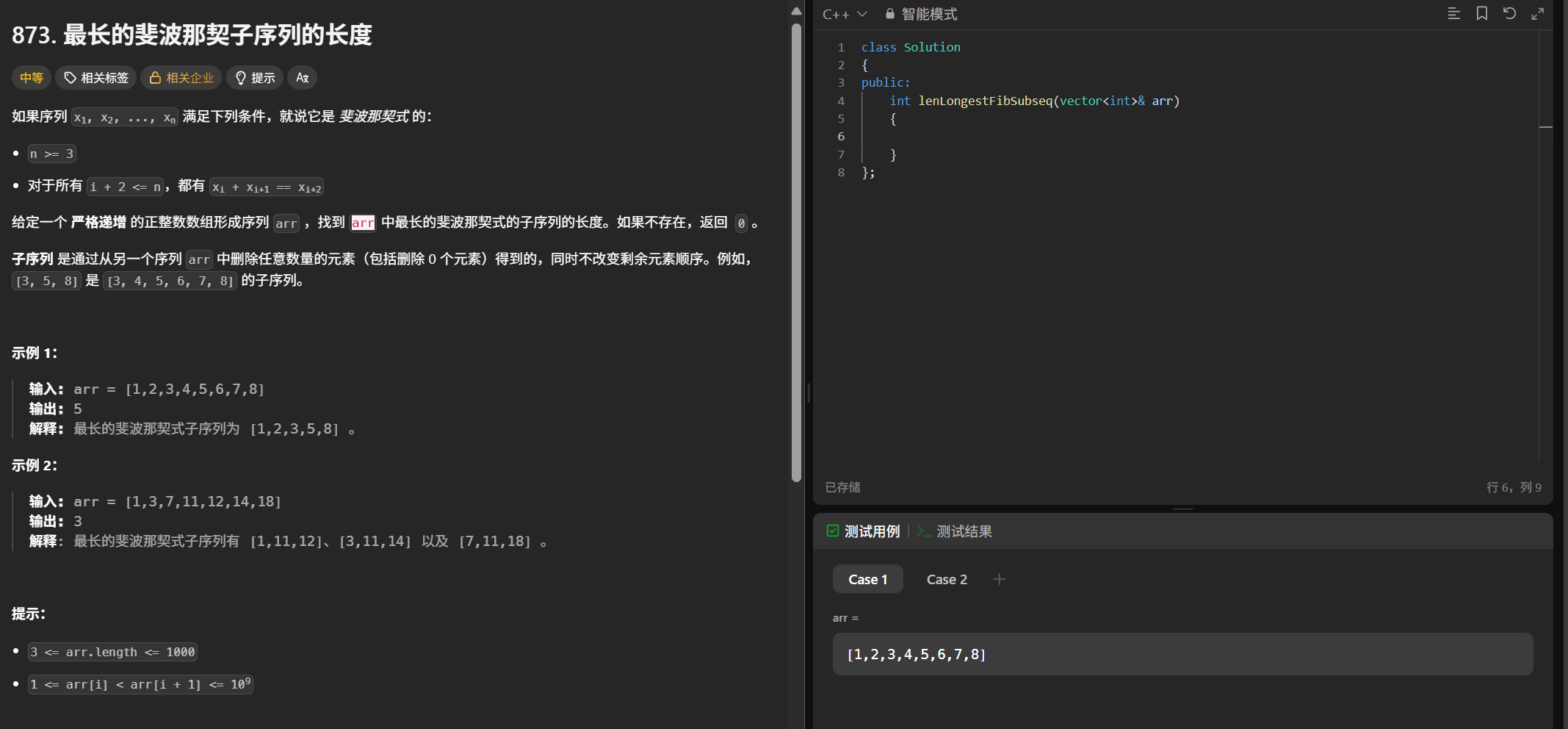
（2）解题思路

状态表示

如果我们单纯以i为结尾，那我们看不到其他的斐波那契数，所以我们可以i和j两个数为结尾

dp[i][j]: 表示以i和j为结尾的最长斐波那契数

状态转移方程

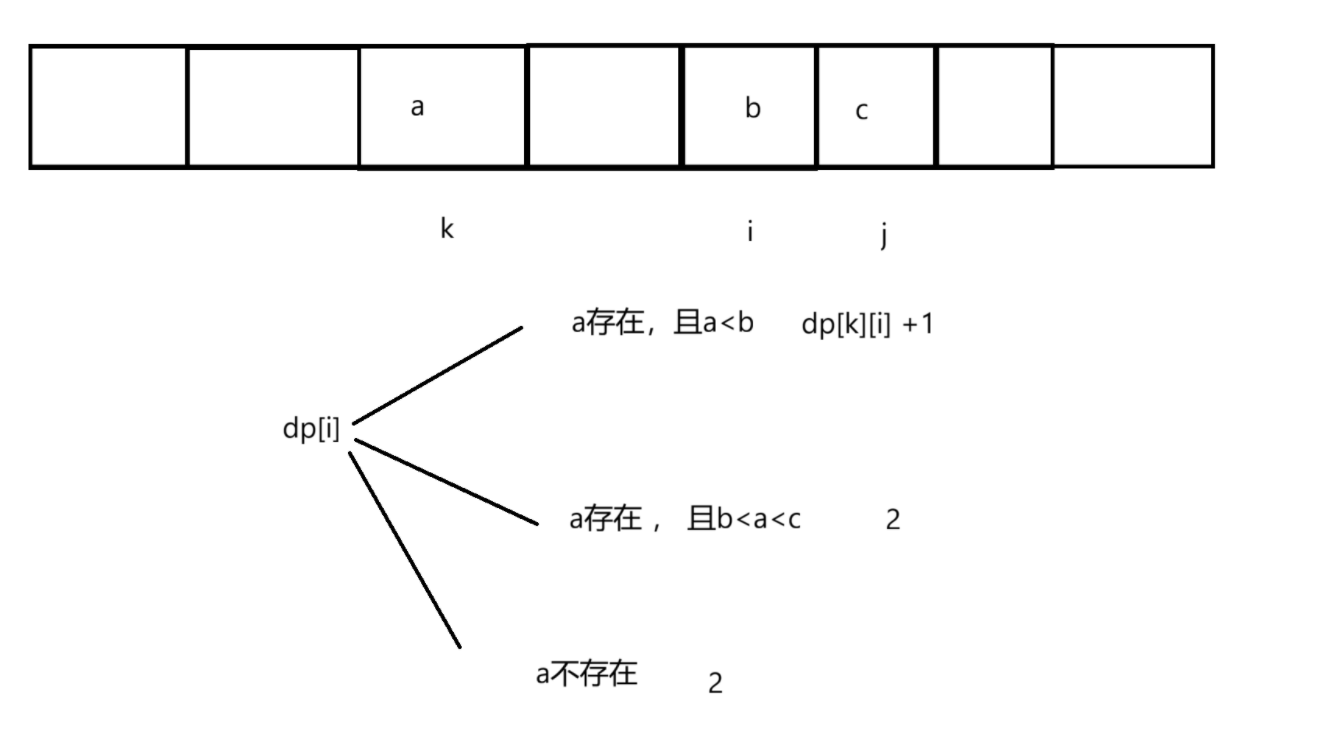
优化：将下标和哈希表绑定

初始化

初始化为2

填表顺序

从上往下

返回值

返回最大的dp[i]

（3）代码实现

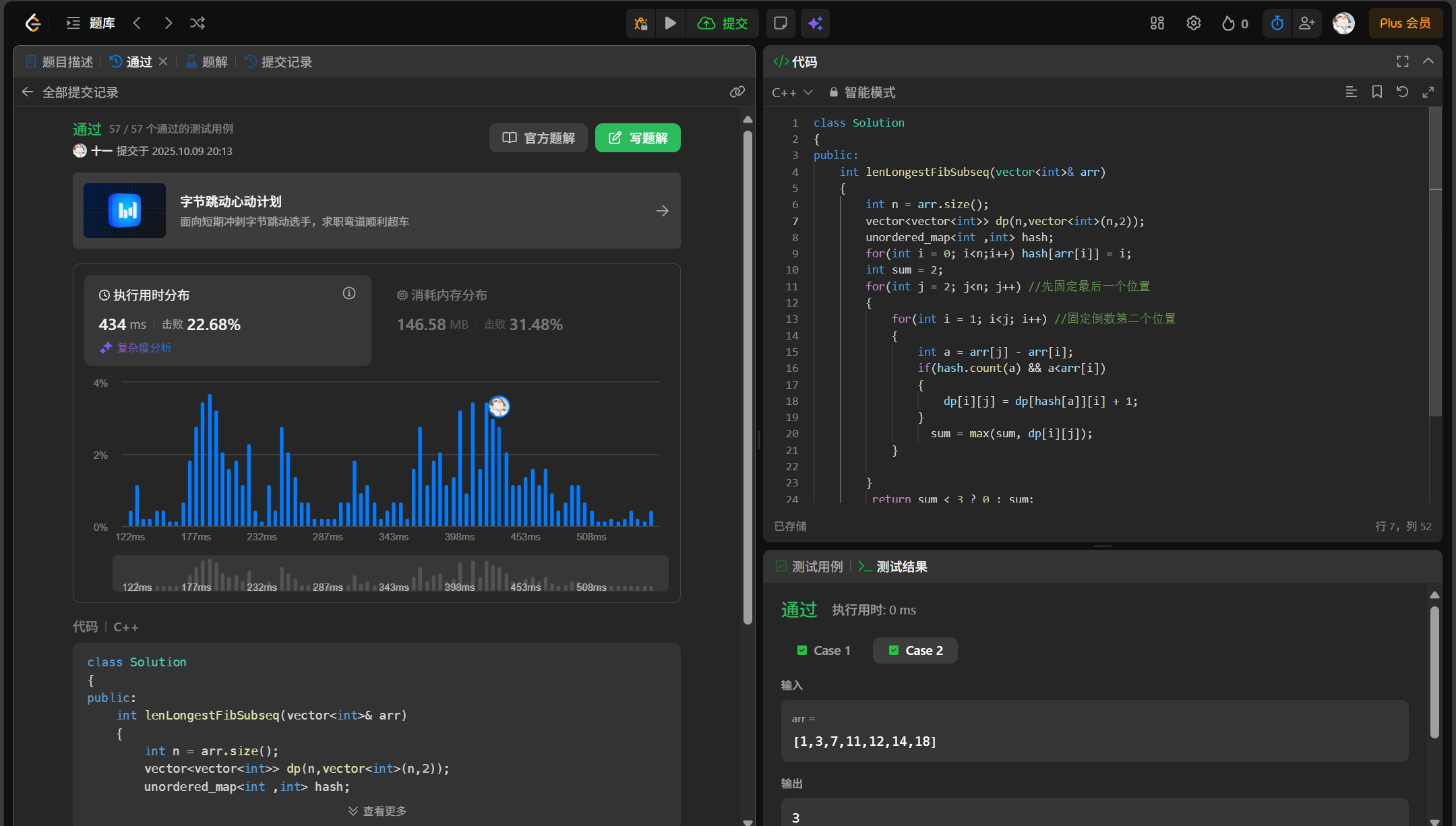
cpp 复制代码

class Solution 
{
public:
    int lenLongestFibSubseq(vector<int>& arr) 
    {
        int n = arr.size();
        vector<vector<int>> dp(n,vector<int>(n,2));
        unordered_map<int ,int> hash;
        for(int i = 0; i<n;i++) hash[arr[i]] = i;
        int sum = 2;
        for(int j = 2; j<n; j++) //先固定最后一个位置
        {
            for(int i = 1; i<j; i++) //固定倒数第二个位置
            {
                int a = arr[j] - arr[i]; 
                if(hash.count(a) && a<arr[i])
                {
                    dp[i][j] = dp[hash[a]][i] + 1;
                }
                  sum = max(sum, dp[i][j]);
            }
           
        }
         return sum < 3 ? 0 : sum;
    }
};

最长等差数列

https://leetcode.cn/problems/longest-arithmetic-subsequence/description/

（1）题目

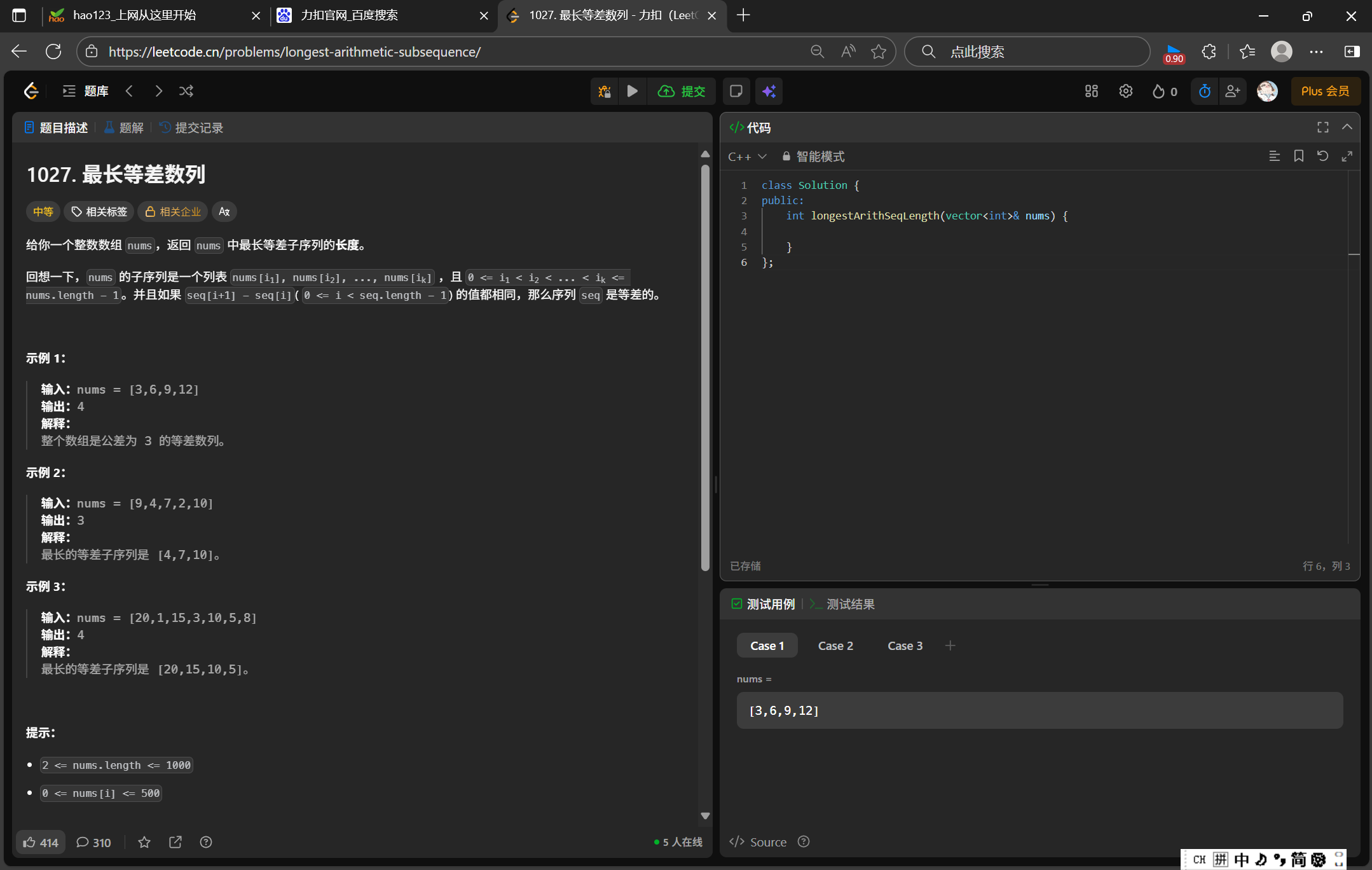
（2）解题思路

状态表示

以i 为结尾，dp[i]表示以i位置为结尾的最长等差序列的长度

该状态表示我们不知道其他的数和公差，所以我们以i,j为结尾

dp[i][j] : 表示以i和j位置为结尾的最长等差序列的长度

状态转移方程

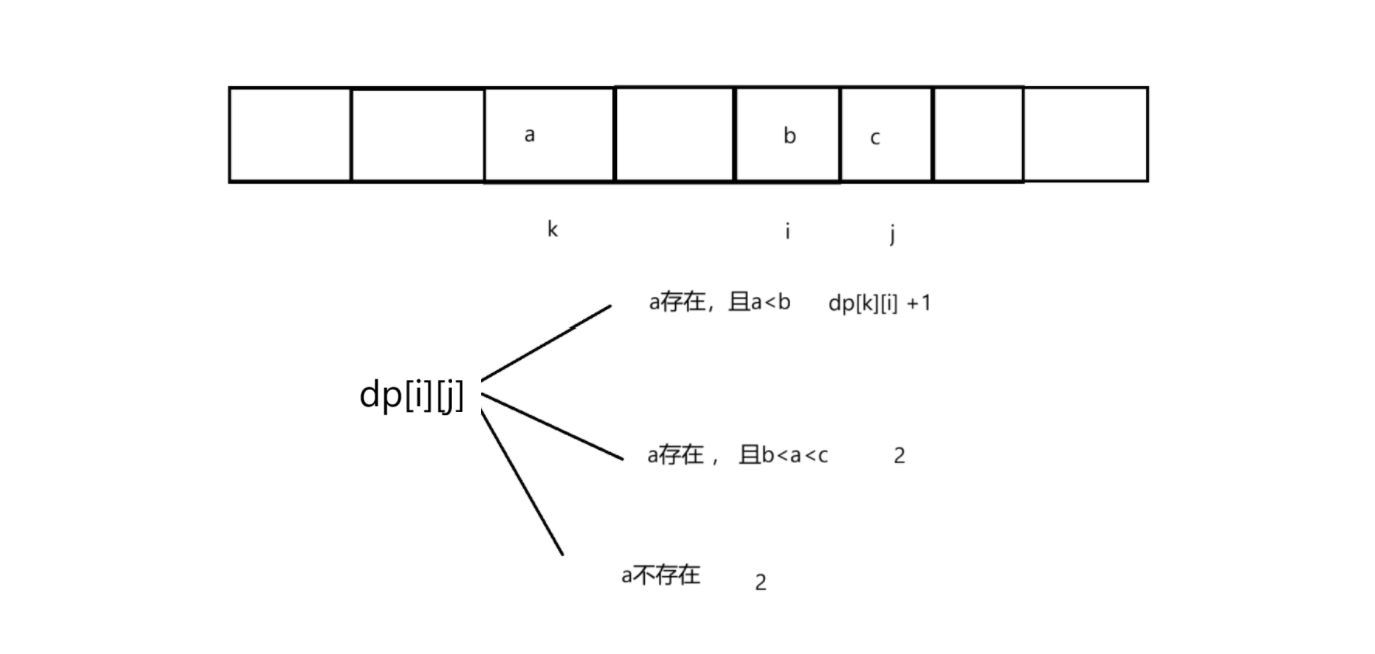
优化：一边dp ,一边保存离它最近的元素下标（为了确保距离倒数第二个元素最近，所以我们需要固定倒数第二个元素的位置）

初始化

dp表中所有的值，都初始化为2

填表顺序

先固定倒数第二个数，枚举最后一个数

返回值

dp表中最大的值

（3）代码实现

cpp 复制代码

class Solution {
public:
    int longestArithSeqLength(vector<int>& nums) 
    {
        unordered_map<int ,int> hash;
        hash[nums[0]] = 0;
        int n = nums.size();
        vector<vector<int>> dp(n,vector<int>(n,2));
        int ret = 2;
        for(int i = 1; i<n;i++)
        {
            for(int j = i+1; j<n;j++)
            {
                 int a = 2*nums[i] - nums[j];
                 if(hash.count(a))
                 {
                    dp[i][j] = dp[hash[a]][i] + 1;
                    
                 }
                 ret = max(ret,dp[i][j]);
            }
            hash[nums[i]] = i;
        }
        return ret;
    }
};

等差数列划分|| - 子序列

https://leetcode.cn/problems/arithmetic-slices-ii-subsequence/description/

（1）题目

（2）解题思路

状态标识

以i为结尾，dp[i]表示以i位置为结尾的等差子序列的长度

因为如果只以i,为结尾我们不知道等差序列的公差和其他序列，所以我们以i和j为结尾

dp[i][j]：表示以i和j为结尾的等差子序列的个数

状态转移方程

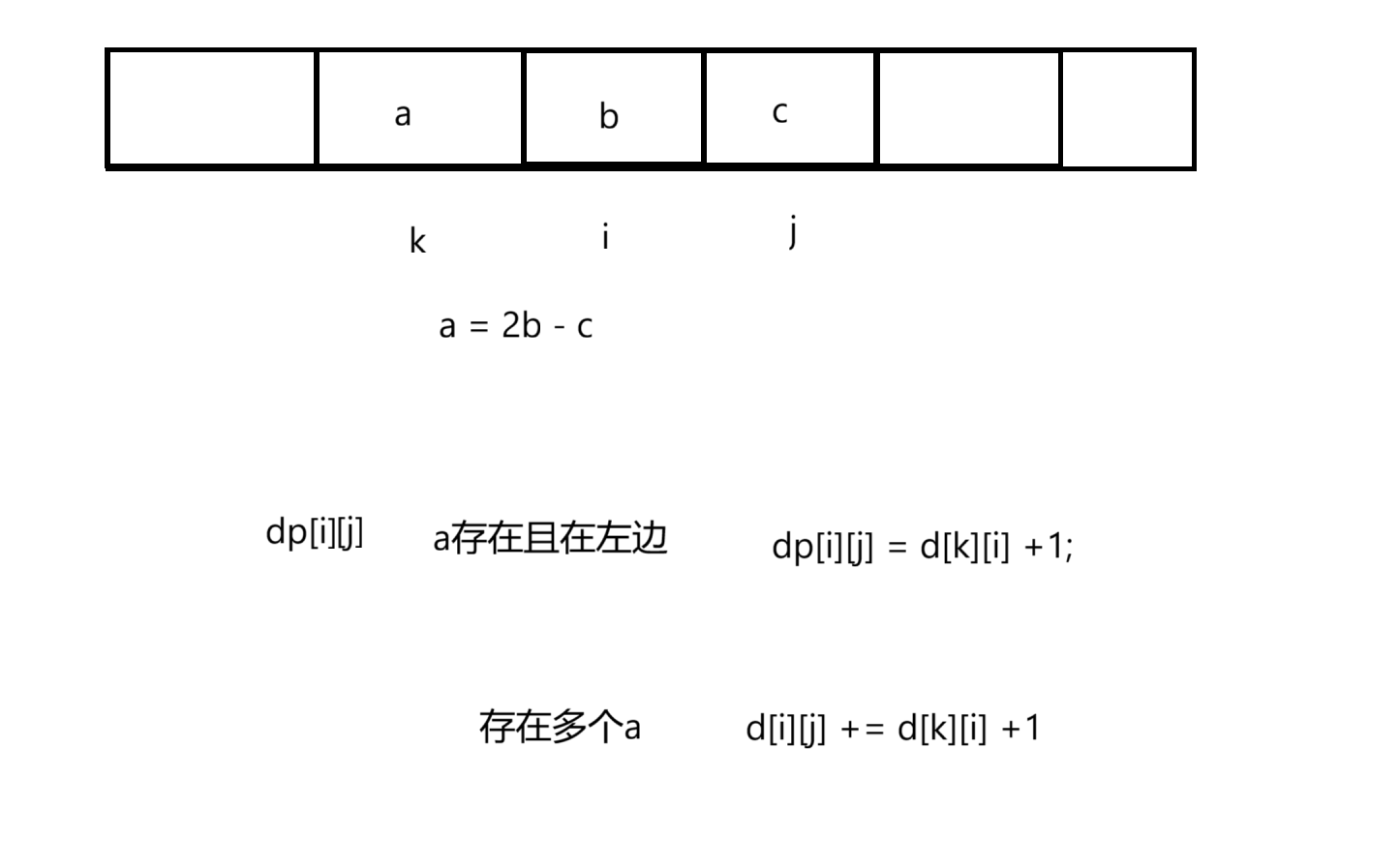
优化

我们寻找a的时候，可以先将元素和数组绑定，以至于快速的寻找到a

初始化

dp表初始化为0

填表顺序

固定最后一个数字

从左到右

返回值

整个dp表相加

（3）代码实现

cpp 复制代码

class Solution
{
public:
    int numberOfArithmeticSlices(vector<int>& nums) 
    {
        int n = nums.size();
        unordered_map<long long ,vector<int>> hash;
        for(int i = 0; i<n; i++) hash[nums[i]].push_back(i);
        vector<vector<int>> dp(n,vector<int>(n));
        int sum = 0;
        for(int j = 2; j<n;j++)
        {
            for(int i = 1; i<j; i++)
            {
                long long a = (long long)2 * nums[i] - nums[j];
                if(hash.count(a))
                {
                    for(auto k : hash[a])
                    {
                        if(k<i)
                        {
                            dp[i][j] += dp[k][i] +1;
                        }
                    }
                }
                sum += dp[i][j]; 
            }
        }
        return sum;
    }
};