0x3f 第19天 javase黑马81-87 ，三更1-23 hot100子串

子串的前缀和预处理

比如 nums=[1,2,3,4,5,6]，要想计算子数组 [3,4,5] 的元素和，可以用前缀 [1,2,3,4,5] 的元素和，减去另一个前缀 [1,2] 的元素和

理解「空间换时间」的思想：用 __init__ 预处理前缀和数组（牺牲 O (n) 空间）

用O (n) 空间得到子串的前缀和，对于实际工程中（如数据库查询、缓存系统）的常见场景 ------ 预处理的价值正是体现在 "多次复用" 上

两处错误

复制代码

class NumArray:

    def __init__(self, nums: List[int]):
        s = [0]*(len(nums)+1)
        for i,x in enumerate(nums):
            s[i+1]=s[i]+x
        ----------------

    def sumRange(self, left: int, right: int) -> int:
        return self.s[right+1]-self.s[left-1]

1.init函数里必须写上self.s =s

s 是 __init__ 里的局部变量 ，如果不赋值给 self.s，__init__ 执行完后 s 就会被 Python 回收，sumRange 方法根本找不到这个前缀和数组；
self.s = s 相当于给实例 "存了个档"，把计算好的前缀和数组永久存在实例里，后续调用任何方法（比如 sumRange）都能通过 self.s 访问到。

2.包含left和right之间的nums元素和：

return self.s[right+1]-self.s[left-1]

应该是return self.s[right+1]-self.s[left]，因为s[left]保存的是 0-left-1 的前缀和！

时间复杂度O（n）空间复杂度O(n)

复制代码

class NumArray:

    def __init__(self, nums: List[int]):
        s = [0]*(len(nums)+1)
        for i,x in enumerate(nums):
            s[i+1]=s[i]+x
        self.s=s

    def sumRange(self, left: int, right: int) -> int:
        return self.s[right+1]-self.s[left]

和为k的子数组

不能用滑动窗口，因为有负数，滑动窗口需要满足单调性，当右端点元素进入窗口时，窗口元素和是不能减少的

零神解答加上视频具体事例，搭配食用效果极佳

https://www.bilibili.com/video/BV1gN411E7Zx/?spm_id_from=333.337.search-card.all.click&vd_source=b5cc04f324fc9d6ee48a5febd77392fc

1.核心思想包括

1.前缀和s，因此可以把题目化简为求s 中有多少对下标 (i,j) 满足s[j]−s[i]=k？

1.1写成 s[j]+(−s[i])=k 就能看得更明白，这是梦开始的地方------1. 两数之和

1.2两数之和的思路就是枚举右端点，不断存入哈希表，遇到满足的target-right的left

去哈希表里查找有没有遍历到过 left

2.引入cnt记录枚举过的s[j]，key为s[j]

2.1对于本题就是for sj in s:

去cnt里找sj-k

比如遍历到s[j]=16这个情况，16-k=10，发现前面的cnt[10]有两个，那就直接说明有两解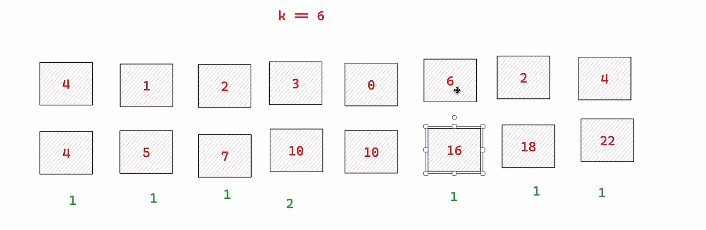

一些额外的思考，关于cnt这个小东西的

这种习惯不是强制的，但符合 "见名知意" 的编码原则 ------ 看到 Counter 就知道是 "统计频次"，看到 defaultdict(int) 就知道是 "通用计数"。

之前遇到过cnt = Counter（）

这个题是 cnt = defaultdict(int)，但是发现使用的目的是相同的，就引发了些思考

总结一下就是

在力扣的字符串类题目中（比如找异位词、最长无重复子串、字符频率统计），开发者的默认习惯是：

只要涉及「字符频次」，优先用 Counter（无需额外思考，语义直观）；

defaultdict(int) 更多用在「非字符计数场景」（比如前缀和次数、数字出现次数、自定义对象计数）。

复制代码

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        s = [0]*(len(nums)+1)
        ans = 0
        for i,x in enumerate(nums):
            s[i+1] = s[i]+x
        cnt = defaultdict(int)
        for sj in s:
            ans += cnt[sj-k]
            cnt[sj]+=1
        return ans

优化：边求前缀和，边找和为k 的解

复制代码

class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        ans = 0
        cnt = defaultdict(int)
        cnt[0]=1
        s=0
        for x in nums:
            s +=x
            ans+=cnt[s-k]
            cnt[s]+=1
        return ans