算法基础练习总结入口:我的算法地图
文章目录
一、基本概念
算法题 里面有一类相对特殊的题目 涉及数学原理。本质是因为数学是算法设计的 "底层逻辑" 和 "高效工具",很多问题的本质是数学问题,或需要用数学原理简化求解;leetcode&面试 数学相关题目并非都需要高深理论,多数是「基础数学概念 + 算法思维」的结合。如果是ACM等竞赛相关,会涉及更多的数学原理内容,有更高要求。
1、本次总结围绕基础数学内容(非竞赛类型),相关概念整理如下:
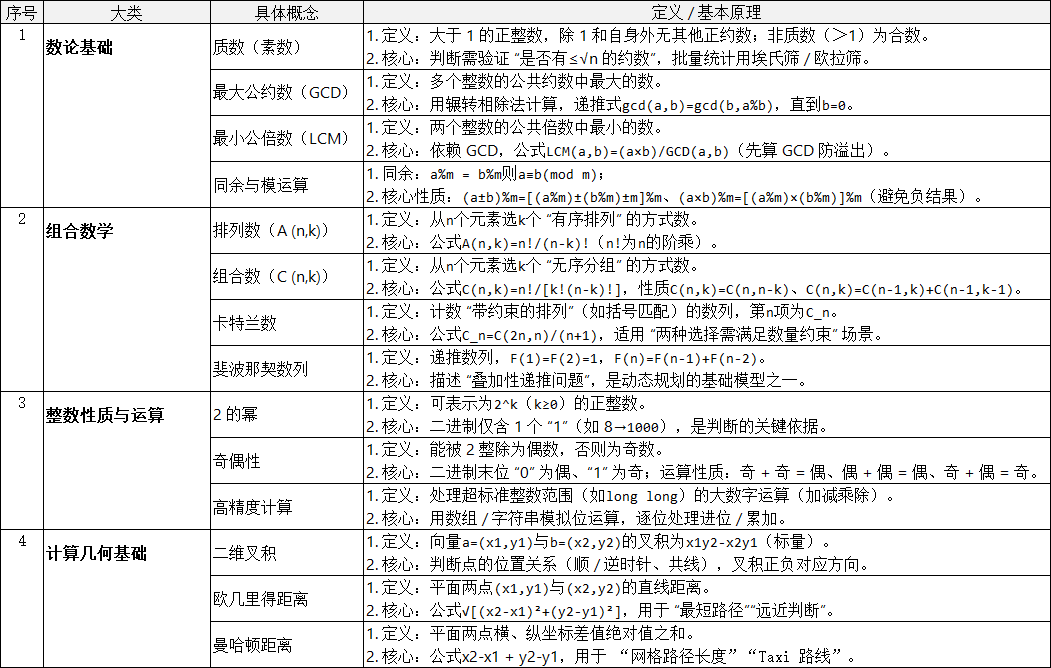
2、相对其他非数学题目,数学类算法题目注意事项:
数学题需先吃透基础概念(如质数、GCD、模运算)再上手 ,非数学题可边练边熟悉数据结构操作或流程逻辑;数学题核心是把问题抽象成数学模型(如转化为组合数、卡特兰数),非数学题侧重拆解需求为具体执行步骤;数学题练习要归纳通用模板 + 验证原理(如埃氏筛、辗转相除法),非数学题需适应场景变体 + 调试操作细节(如链表指针、窗口边界);
二、场景分析
1、按题目类型进行总结
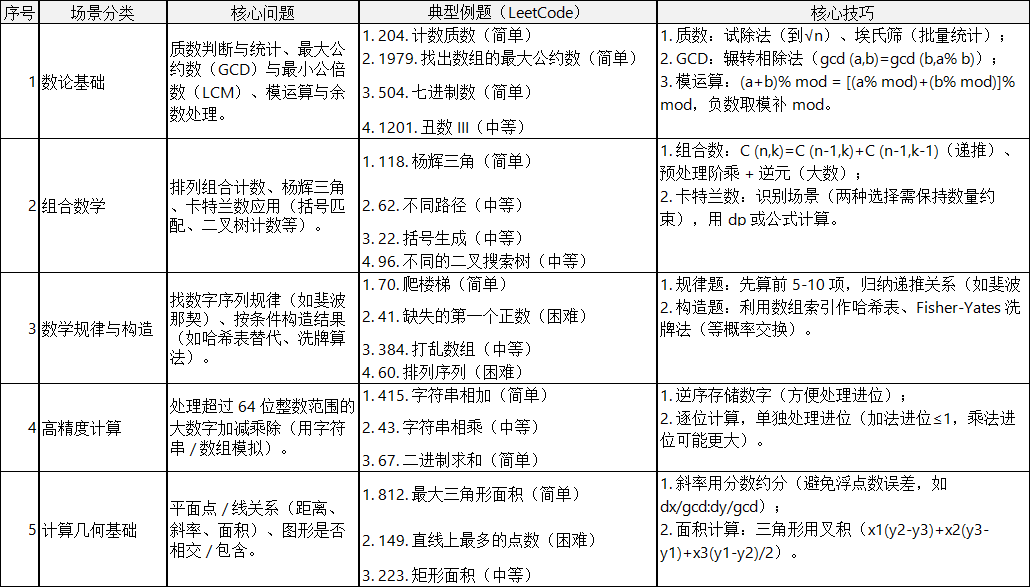
2、相关技巧总结
1)看题目是否含明确数学概念(如质数、GCD、组合数、卡特兰数),有则优先用数学;
2)若需计算特殊结果(如面积、大数字加减、排列数),或涉及数字性质(如 2 的幂、余数),用数学;
3)常规方法(暴力、模拟)超时 / 复杂时,排查是否有数学规律(递推公式、数论性质)可简化;
4)遇到 "计数、优化计算、数字关系判断" 类问题,优先联想数学工具(如筛法、模运算、叉积)。
三、典型题目
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
cpp
// 思路1:枚举法,结果超时。
bool isPrime(int n) {
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
public:
int countPrimes(int n) {
int cnt = 0;
for (int i = 2; i < n; i++) {
cnt += isPrime(i);
}
return cnt;
}
//------------------------------------------------------------------
// 思路2:埃氏筛。如果 x 是质数,那么大于 x 的 x 的倍数 2x,3x,... 一定不是质数。
int countPrimes(int n) {
vector<int> isprime(n, 1); // 先都初始化为都是质数
int cnt = 0;
for (int i = 2; i < n; i++) { // 从最小质数2开始遍历
if (isprime[i]) {
cnt++;
// 标记i的所有倍数为非质数(从i*i开始,优化效率)
if ((long long) i * i < n) {
// 从i*i开始(而非2i),因为i*2, i*3...i*(i-1)早已被比i小的质数标记过
for (int j = i * i; j < n; j += i) {
isprime[j] = 0; // j是i的倍数,标记为非质数
}
}
}
}
return cnt;
}埃氏筛:如果一个数i是质数,那么它的所有倍数(2i, 3i, 4i...)一定不是质数,可直接标记为非质数。
优化点:标记倍数时从ii开始(而非2i),因为i 2, i3...i (i-1)早已被比i小的质数(如 2,3...i-1)标记过(例如i=5时,52=10已被 2 标记,5 3=15已被 3 标记,只需从55=25开始标记)。防溢出处理:(long long)i * i < n确保计算ii时不会因i过大导致 int 类型溢出(如i=46340时,i*i约为 2e9,超过 int 最大值,转为 long long 可正确判断)。
给你一个整数数组 nums ,返回数组中最大数和最小数的 最大公约数 。两个数的 最大公约数 是能够被两个数整除的最大正整数。
cpp
int getgcd(int a, int b) {
while (a % b) {
int remain = a % b;
a = b;
b = remain;
}
return b;
}
public:
int findGCD(vector<int>& nums) {
// 思路:数学 辗转相除法
int max = nums[0];
int min = nums[0];
for (auto &num : nums) {
if (num > max) {
max = num;
}
if (num < min) {
min = num;
}
}
return getgcd(min, max);
}辗转相除法是快速求两个正整数最大公约数(GCD) 的经典算法,核心是利用 "余数递推" 大幅降低计算量,比暴力枚举效率高得多。对任意两个正整数 a(较大数)和 b(较小数,b≠0),满足:gcd(a, b) = gcd(b, a % b)(a % b 表示 a 除以 b 的余数,结果范围是 0 ≤ 余数 < b)。终止条件:当余数 a % b = 0 时,此时的 b 就是原来两个数的 GCD。
给定一个整数 num,将其转化为 7 进制,并以字符串形式输出。
cpp
string convertToBase7(int num) {
// 思路:数学 倒推
if (num == 0) {
return "0";
}
bool negative = num < 0;
num = abs(num);
string ret;
while (num > 0) {
ret.push_back(num % 7 + '0');
num /= 7;
}
if (negative) {
ret.push_back('-');
}
reverse(ret.begin(), ret.end());
return ret;
}丑数是可以被 a 或 b 或 c 整除的 正整数 。给你四个整数:n 、a 、b 、c ,请你设计一个算法来找出第 n 个丑数。
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。在「杨辉三角」中,每个数是它左上方和右上方的数的和。
cpp
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ret(numRows);
for (int i = 0; i < numRows; ++i) {\
// 调整当前行的长度为i+1
ret[i].resize(i + 1);
// 设置当前行的首尾元素为1
ret[i][0] = ret[i][i] = 1;
// 计算当前行的中间元素(j从1到i-1,即非首尾位置)
for (int j = 1; j < i; ++j) {
// 中间元素 = 上一行相邻两元素之和
ret[i][j] = ret[i - 1][j] + ret[i - 1][j - 1];
}
}
return ret;
}