图论专题(二)：“关系”的焦点——一眼找出「星型图的中心节点」

哈喽各位，我是前端小L。

欢迎来到我们的图论专题第二篇！上一节我们用DFS/BFS解决了"路径是否存在"的问题，可以说是"牛刀小试"。今天，我们来换个口味，看一个更像是"脑筋急转弯"的图论题。

这道题将教会我们，有时，解决图论问题，并不一定需要启动复杂的遍历算法。抓住图的"形态"特征，比如"星型图"的"中心"属性，我们可以找到 O(1) 的"神之捷径"。

力扣 1791. 找出星型图的中心节点

https://leetcode.cn/problems/find-center-of-star-graph/

题目分析：

输入：一个 edges 数组，代表一个"星型图"的所有边。
星型图 ：一个 n 个节点的图，有 n-1 条边，并且有且仅有 一个"中心节点"，所有其他 n-1 个节点都只和这个中心节点相连。
目标：找到这个中心节点。

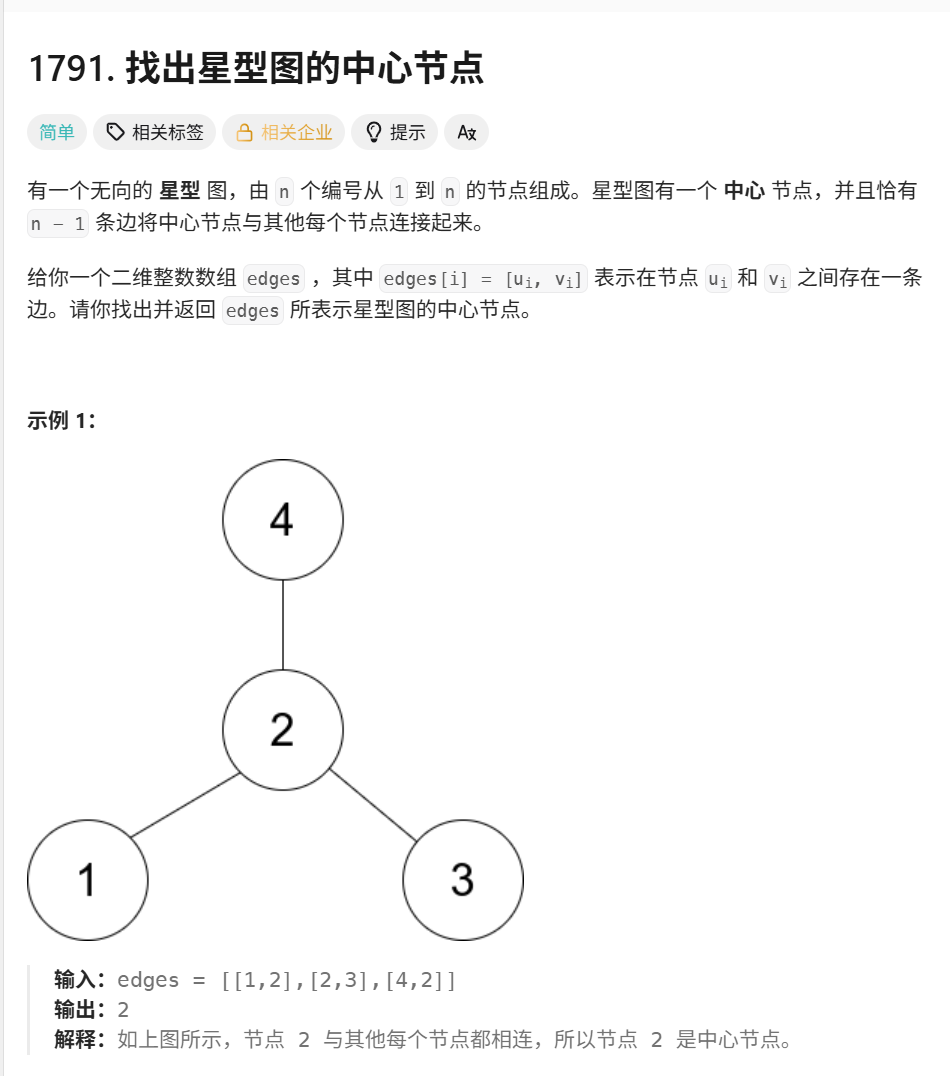
例子： edges = [[1, 2], [2, 3], [4, 2]]

节点 1, 3, 4 都只连接到了 2。
2 连接到了 1, 3, 4。
2 就是中心节点。

思路一："科班"出身的解法------统计"度" (O(V+E))

我们刚学了图论，最"科班"的做法是什么？

建图：还是用"邻接表" vector<vector<int>> graph(n + 1) (注意这题节点从1开始，所以大小是 n+1)。
统计度 ：遍历 edges，构建邻接表。
寻找中心 ：遍历邻接表 graph (从 i=1 到 n)。
- "度"(degree) 就是一个节点的邻居数量，即 graph[i].size()。
- 根据"星型图"的定义，中心节点的"度"一定是 n - 1。
- if (graph[i].size() == n - 1) return i;

评价：

时间复杂度 O(V + E) ：V=n, E=n-1。建图需要 O(E)，遍历 graph 需要 O(V)。总时间 O(V+E)。
空间复杂度 O(V + E)：邻接表需要 O(V+E) 空间。
这是一个"万金油 "解法，它不依赖"星型图"的特殊性，只要是找"度"最大的节点（在本题中恰好是 n-1），它都适用。

思路二："Aha!"时刻------O(1) 的"神之捷径"

让我们再读一遍题："星型图"、"n-1 条边"、"一个中心节点"。这意味着，中心节点，必然会出现在每一条边上！

edge[0] = [center, node_A]
edge[1] = [node_B, center]
edge[2] = [center, node_C]
...

既然它无处不在 ，我们还需要遍历所有边吗？ 不需要！ 我们只需要随便拿出两条边 ，找出它们共同的那个节点，就一定是中心！

算法流程 (O(1))：

题目保证 n >= 3，这意味着至少有 n-1 = 2 条边。
取出第一条边 edges[0]，它包含两个节点：u = edges[0][0] 和 v = edges[0][1]。
取出第二条边 edges[1]。
检查：u 是否也出现在 edges[1] 中？
- if (u == edges[1][0] || u == edges[1][1])
  - 是！u 连续出现了两次，它就是中心。return u。
否则：
- u 不是中心，那么根据星型图的定义，v 一定是中心。return v。

代码实现

解法一：统计度 (O(V+E))

C++

复制代码

#include <vector>

using namespace std;

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        int n = 0;
        // 1. 先找出n (最大的节点编号)
        // 也可以用 edges.size() + 1，因为有 n-1 条边
        n = edges.size() + 1;
        
        // 2. 建图并统计度 (使用 vector 代替 map)
        vector<int> degree(n + 1, 0); // 节点从1到n
        
        for (const auto& edge : edges) {
            degree[edge[0]]++;
            degree[edge[1]]++;
        }
        
        // 3. 寻找度为 n-1 的节点
        for (int i = 1; i <= n; ++i) {
            if (degree[i] == n - 1) {
                return i;
            }
        }
        return -1; // 题目保证一定存在，不会到这里
    }
};

(自我修正：邻接表 vector<vector<int>> 其实都不需要，只需要一个 vector<int> degree 数组来计数即可，时空复杂度都优化到了 O(V) 和 O(E)) (再次修正：建图O(E)，统计O(E)，遍历O(V)。总时间 O(V+E)，空间 O(V))

解法二：O(1) 捷径

C++

复制代码

#include <vector>

using namespace std;

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        // 题目保证 n >= 3，所以 edges[0] 和 edges[1] 必定存在
        
        // 中心节点一定同时在第一条边和第二条边上
        int u1 = edges[0][0];
        int v1 = edges[0][1];
        
        int u2 = edges[1][0];
        int v2 = edges[1][1];
        
        if (u1 == u2 || u1 == v2) {
            return u1;
        } else {
            // 既然 u1 不是，那 v1 必定是
            return v1;
        }
    }
};

深度复杂度分析 (O(1) 解法)

时间复杂度 O(1)：
- 我们只访问了 edges[0] 和 edges[1]，进行了常数次（最多2次）比较。
- 操作次数是恒定的，与 n 的大小无关。
空间复杂度 O(1)：
- 只使用了 u1, v1, u2, v2 四个额外变量。

总结

今天这道"热身题"，从两个角度给了我们启发：

"度" (Degree) 是图论中一个极其重要的基础概念，通过graph[i].size() 或 degree[i] 计数，是解决很多问题的钥匙。
"利用题目约束" 是成为算法高手的"捷径"。当题目给出了"星型图"这样强有力的约束时，一定要思考，这个约束能否让我们绕开"通用但昂贵"的算法，找到 O(1) 或 O(log n) 的"神之一手"？

在下一篇中，我们将回归"遍历"的主线，去解决一个更生动的"钥匙与房间"的问题。

下期见！