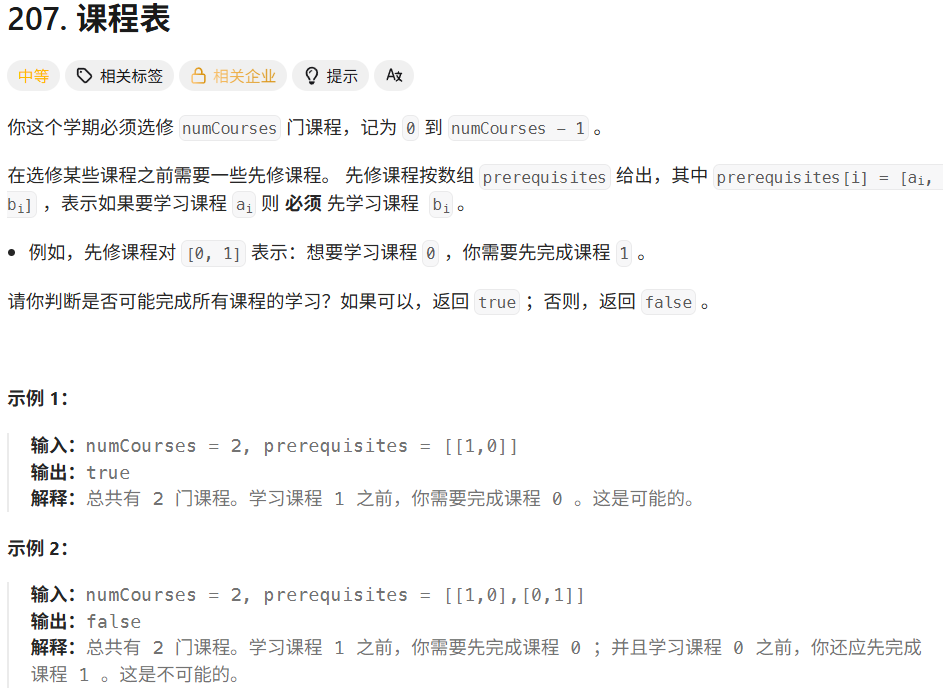
解法
题解中的广度优先算法
直接运用拓扑排序中的找入度为0的点的方法,就可以了。非常地清晰。
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
List<List<Integer>>edgs=new ArrayList();
int []flag=new int[numCourses];
for(int i=0;i<numCourses;i++){
edgs.add(new ArrayList<Integer>());
}
for(int[]nums:prerequisites){
edgs.get(nums[1]).add(nums[0]);
flag[nums[0]]++;
}
Queue<Integer>queue=new LinkedList();
for(int i=0;i<numCourses;i++){
if(flag[i]==0){
queue.offer(i);
}
}
int visited=0;
while(!queue.isEmpty()){
visited++;
int tmp=queue.poll();
for(int v:edgs.get(tmp)){
flag[v]--;
if(flag[v]==0){
queue.offer(v);
}
}
}
return visited==numCourses;
}
}题解中的深度优先搜索
用图的数据结构来解题,将数组变成有向图。List<List<Integer>>外面是头,结束是尾。
三种状态,未访问(0),正在访问(1),访问过(2)
正在访问的时候发现访问到了正在访问的节点(有点绕,但想一下)就说明有环,访问到自己了。直接从栈里面弹出去(return)。如果已经知道存在环(flag=false)就直接弹出去(return),如果没有发现环,就正常地让节点进入到"访问过的状态(2)".
我在做这道题的时候遇到的一个问题就是,我开始没有搞明白题解中的return 是什么意思,dfs这个方法不需要返回什么东西,如果他走完了,可以将节点的状态变为访问过的状态,只有出现异常(发现了环)才会中间强制返回。
class Solution {
List<List<Integer>>edgs;
boolean flag=true;
int []visited;
public boolean canFinish(int numCourses, int[][] prerequisites) {
int n = prerequisites.length;
visited=new int[numCourses];
edgs=new ArrayList<List<Integer>>();
for(int i=0;i<numCourses;i++){
edgs.add(new ArrayList<Integer>());
}
for(int []num:prerequisites){
edgs.get(num[1]).add(num[0]);
}
for(int i=0;i<numCourses&&flag;i++){
if(visited[i]==0){
dfs(i);
}
}
return flag;
}
public void dfs(int i){
visited[i]=1;
for(int v:edgs.get(i)){
if(visited[v]==0){
dfs(v);
if(!flag){
return;
}
}else if(visited[v]==1){
flag=false;
return;
}
}
visited[i]=2;
}
}历史解法
报错超出时间限制的解法
这个方法时间复杂度O(n2)。每次都遍历整个数组,看能不能找到让序列连续下去,我想过用哈希表来做,但是哈希表一次只能存储一个键,比如(1,3)(1,2)只能留下一个。所以我还是直接让复杂度高一些,先做出来再说。
我又想了一下,先决条件,可以继承啊,所以采用Map<Integer,List<Integer>>这种数据结构,后面是前面的先决条件,这样就完美解决了这个问题,选择正确的数据结构的重要性,在这一刻体现出来了!!
在做的过程中我又发现,Map<Integer,Set<Integer>>map=new HashMap();这种数据结构好像更合适。用Map<Integer, Set<Integer>>存储数据,方便找。然后遍历集合,
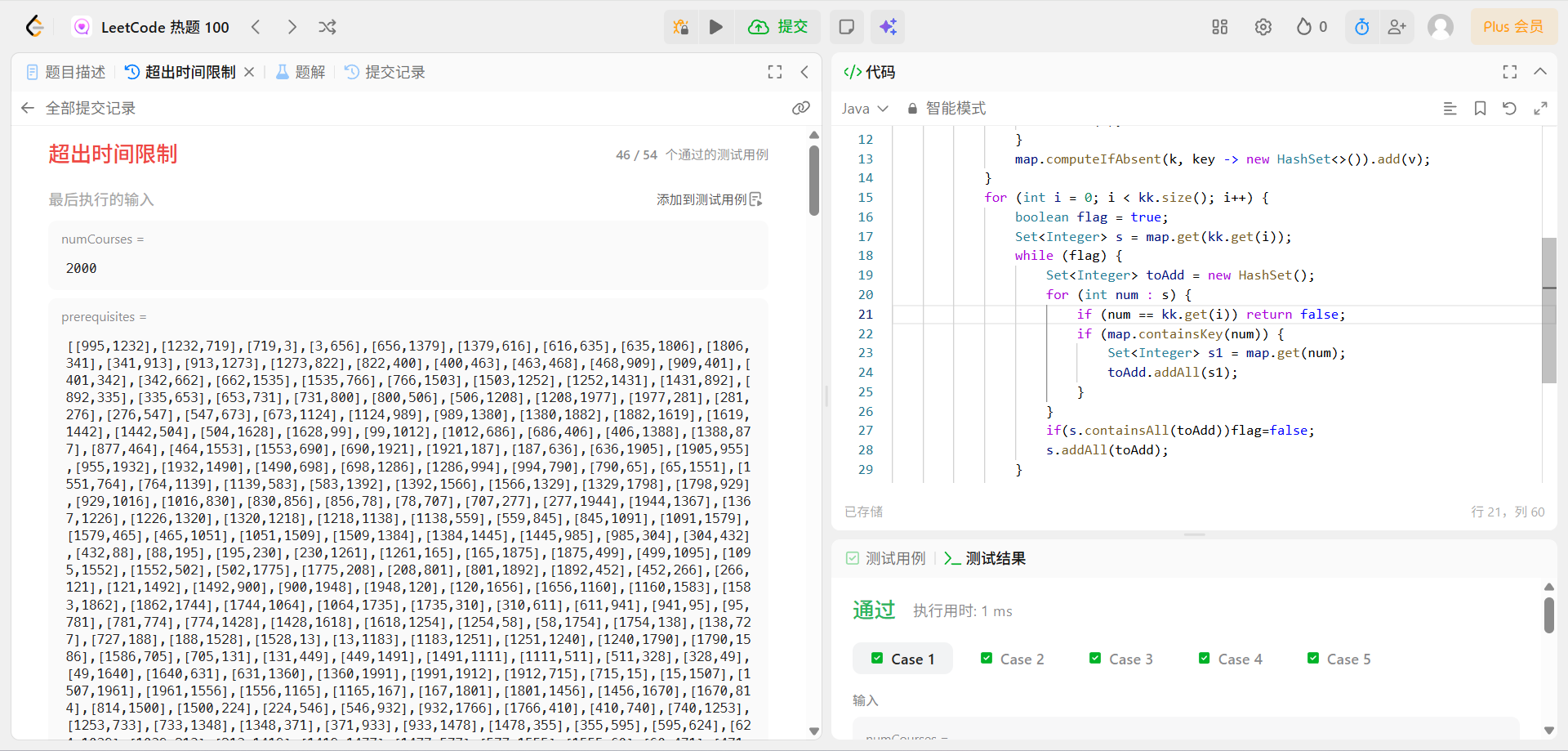
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int n = prerequisites.length;
if (n > numCourses * (numCourses - 1) / 2) return false;
Map<Integer, Set<Integer>> map = new HashMap();
List<Integer> kk = new ArrayList();
for (int i = 0; i < n; i++) {
int k = prerequisites[i][0];
int v = prerequisites[i][1];
if (!map.containsKey(k)) {
kk.add(k);
}
map.computeIfAbsent(k, key -> new HashSet<>()).add(v);
}
for (int i = 0; i < kk.size(); i++) {
boolean flag = true;
Set<Integer> s = map.get(kk.get(i));
while (flag) {
Set<Integer> toAdd = new HashSet();
for (int num : s) {
if (num == kk.get(i)) return false;
if (map.containsKey(num)) {
Set<Integer> s1 = map.get(num);
toAdd.addAll(s1);
}
}
if(s.containsAll(toAdd))flag=false;
s.addAll(toAdd);
}
}
for (int i = 0; i < kk.size(); i++) {
Set<Integer> s = map.get(kk.get(i));
for (int num : s) {
if (num == kk.get(i)) return false;
}
}
return true;
}
}通过了52个例子的解法
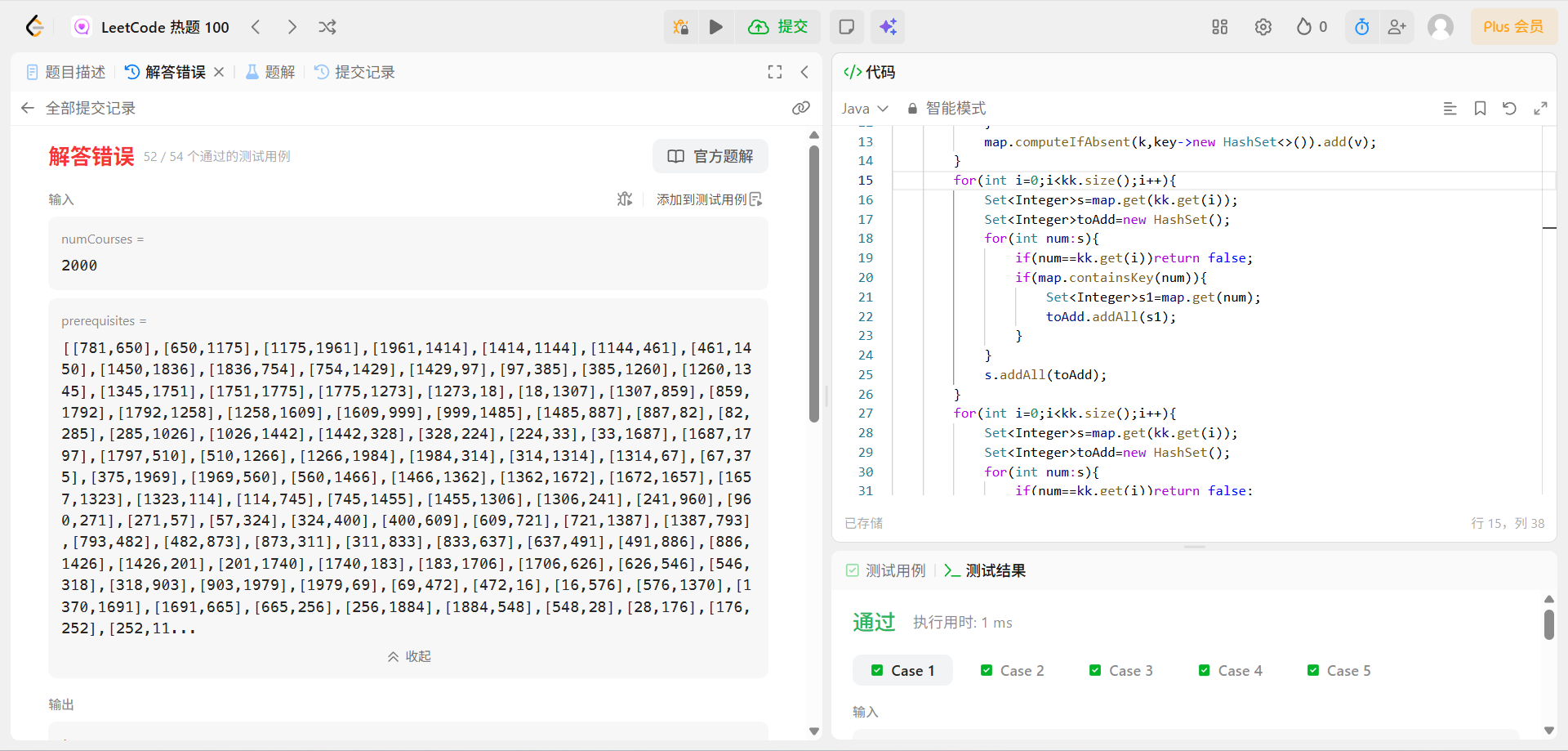
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int n=prerequisites.length;
if(n>numCourses*(numCourses-1)/2)return false;
Map<Integer,Set<Integer>>map=new HashMap();
List<Integer>kk=new ArrayList();
for(int i=0;i<n;i++){
int k=prerequisites[i][0];
int v=prerequisites[i][1];
if(!map.containsKey(k)){
kk.add(k);
}
map.computeIfAbsent(k,key->new HashSet<>()).add(v);
}
for(int i=0;i<kk.size();i++){
Set<Integer>s=map.get(kk.get(i));
Set<Integer>toAdd=new HashSet();
for(int num:s){
if(num==kk.get(i))return false;
if(map.containsKey(num)){
Set<Integer>s1=map.get(num);
toAdd.addAll(s1);
}
}
s.addAll(toAdd);
}
for(int i=0;i<kk.size();i++){
Set<Integer>s=map.get(kk.get(i));
Set<Integer>toAdd=new HashSet();
for(int num:s){
if(num==kk.get(i))return false;
if(map.containsKey(num)){
Set<Integer>s1=map.get(num);
toAdd.addAll(s1);
}
}
s.addAll(toAdd);
}
for(int i=0;i<kk.size();i++){
Set<Integer>s=map.get(kk.get(i));
for(int num:s){
if(num==kk.get(i))return false;
}
}
return true;
}
}