
🔥草莓熊Lotso: 个人主页
❄️个人专栏: 《C++知识分享》 《Linux 入门到实践:零基础也能懂》
✨生活是默默的坚持,毅力是永久的享受!
🎬 博主简介:

文章目录
前言:
聚焦算法题实战,系统讲解三大核心板块:优选算法:剖析动态规划、二分法等高效策略,学会寻找"最优解"。 递归与回溯:掌握问题分解与状态回退,攻克组合、排列等难题。 贪心算法:理解"局部最优"到"全局最优"的思路,解决区间调度等问题 内容以题带点,讲解思路与代码实现,帮助大家快速提升代码能力。
25.【模板】前缀和
题目链接:
题目描述:
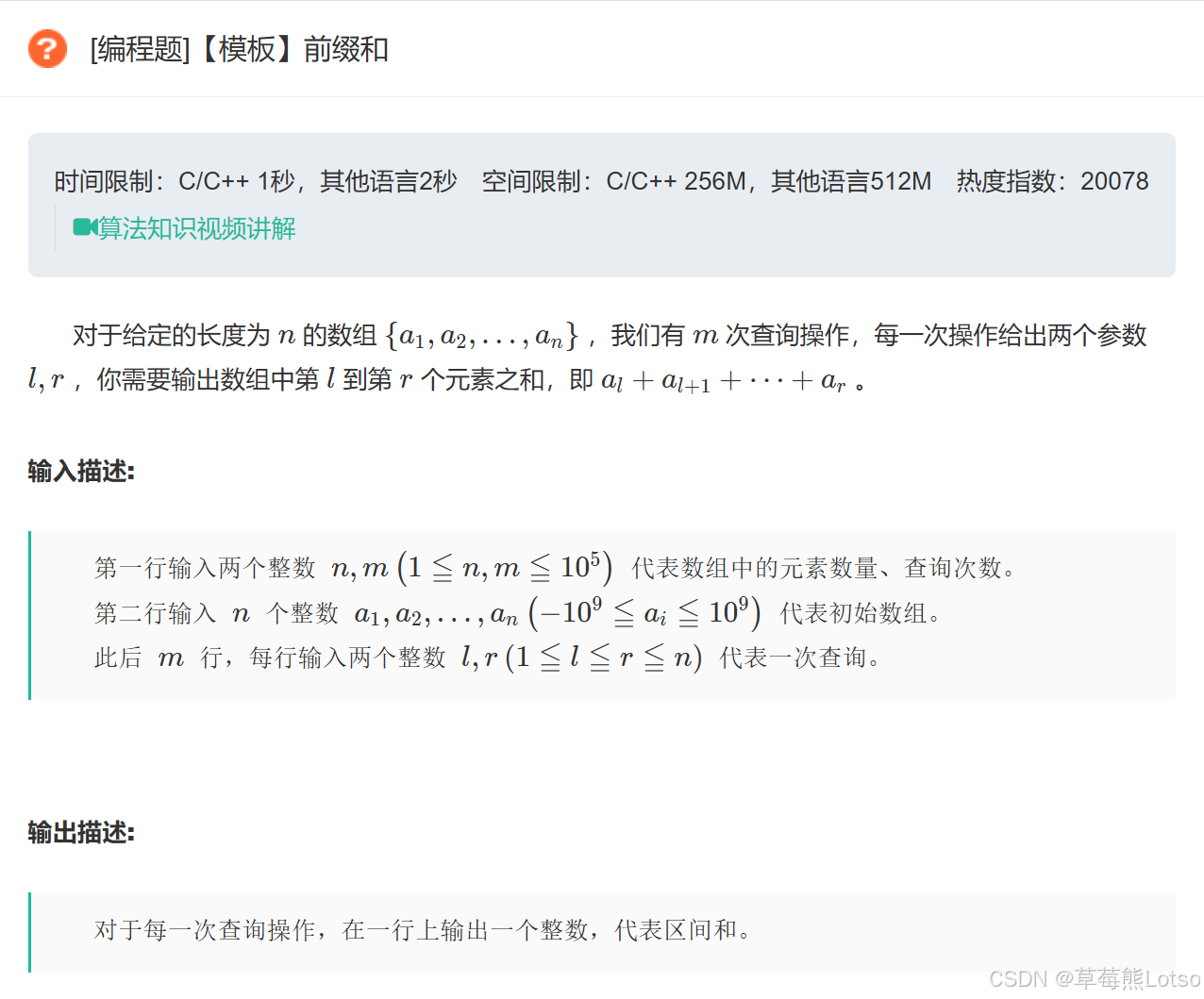
题目示例:

解法(前缀和):
算法思路:
- 先预处理出来一个
【前缀和】数组:用 dp[i] 表示:【1,i】区间所有元素的和,那么dp[i-1]里面存的就是【1,i-1】区间内所有元素的和,那么:可得递推公式:dp[i]=dp[i-1]+arr[i]; - 使用前缀和数组,【快速】求出【某一个区间内】所有元素的和:当询问的区间是
【l,r】时:区间内所有元素的和为:dp[r]-dp[l-1]。
C++算法代码:
cpp
#include <iostream>
#include<vector>
using namespace std;
int main() {
//1.输入数据
int n=0,m=0;
cin>>n>>m;
vector<int> arr(n+1);
for(size_t i=1;i<=n;i++) cin>>arr[i];
//2.预处理一个dp数组
vector<long long> dp(n+1);//防止溢出
for(size_t i=1;i<=n;i++) dp[i]=dp[i-1]+arr[i];
//3.使用前缀和数组
int l=0,r=0;
while(m--)
{
cin>>l>>r;
cout<<dp[r]-dp[l-1]<<'\n';
}
return 0;
}
// 64 位输出请用 printf("%lld")算法总结&&笔记展示:
笔记字有点丑,大家见谅:

26.【模板】二维前缀和
题目链接:
题目描述:

题目示例:
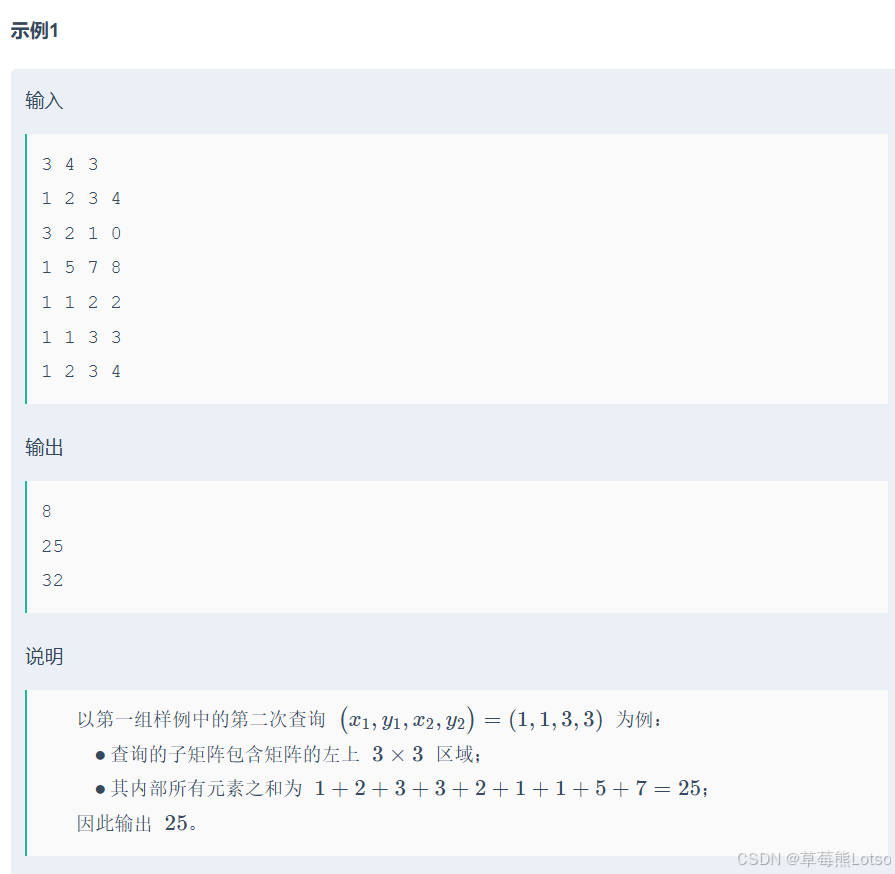
解法:
算法思路:
类比于一维数组的形式,如果我们能处理出来从【0,0】位置到【i,j】位置这片区域内所有元素的累加和,就可以在 O(1) 的时间内,搞定矩阵内任意区域内所有元素的累加和。因此我们需要接下来仅需要完成下面两步即可:
第一步:搞出来前缀和矩阵
这里就要用到一维数组里面的扩展知识,我们要在矩阵的最上面和最左边添加上一行和一列0,这样我们久可省去非常多的边界条件的处理,处理后的矩阵就像下面这样:
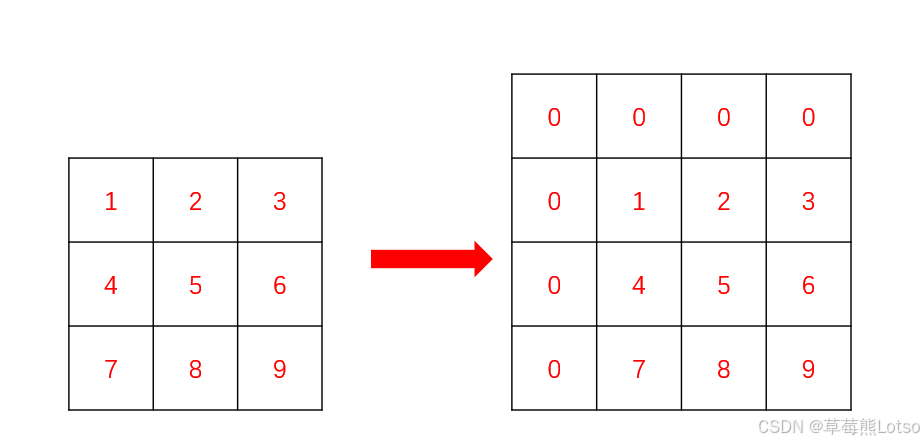
这样,我们填写前缀和矩阵数组的时候,下标直接从 1 开始,能大胆使用 i-1,j-1 位置的值。
注意:
dp表与原数组martix内的元素的映射关系:
- 从
dp表到martix矩阵,横纵坐标减一;- 从
martix矩阵到dp表,横纵坐标加一;
前缀和矩阵中 sum[i][j] 的含义,以及如何递推二维前缀和方程
sum[i][j]表示,从【0,0】位置到【i,j】位置这段区域内,所有元素的累加和。对应下图的红色区域:
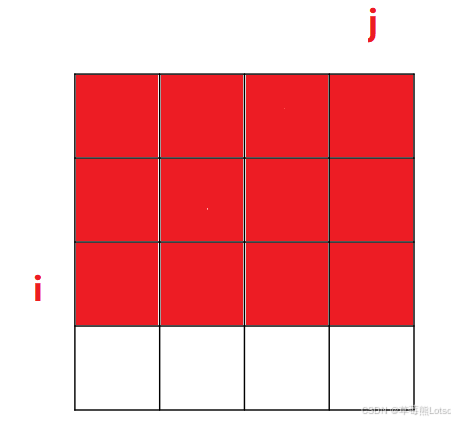
递推方程:
其实这个递推方程非常像我们小学做过的求图形面积的题,我们可以将【0,0】位置到【i,j】位置这段区域分解成下面的部分:

sum[i][j] = 红 + 蓝 + 绿 + 黄,分析一下这四块区域:- 黄色部分最简单,它就是数组中的
martix[i-1][j-1](注意坐标的映射关系) - 单独求蓝色不好求,因为它不是我们定义的状态表示中的区域,同理,单独的绿也是;
- 但是如果是红+蓝,正好是我们
dp数组中sum[i-1][j]的值; - 同理,如果是红+绿,正好是我们
dp数组中sum[i][j-1]的值; - 如果把上面求的三个值加起来,我们会发现多算了一块红色的,因此直接再单独减掉就可以了那就是
黄+(红+蓝)+(红+绿)-红; - 红的面积正好也是符合
dp数组的定义的,即sum[i-1][j-1]。
综上所述,我们的递推方程就是:
sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + martix[i-1][j-1]
第二步:使用前缀和矩阵
题目的接口中提供的参数是原始矩阵的下标,为了避免下标映射错误,这里直接先把下标映射成 dp 表里面对应的下标:row1++,col1+=,row2++,col2++
接下来分析如何使用这个前缀和矩阵,如下图(注意这里的 row 和 col 都处理过了,对应的是 sum 矩阵中的下标):
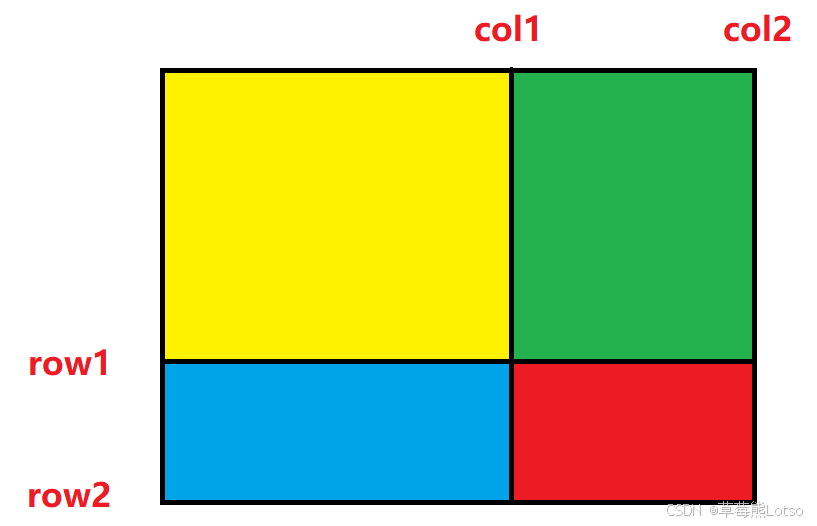
对于左上角(row1,col1),右下角(row2,cow2)围成的区域,正好是红色部分。因此我们需要求的就是红色部分的面积,继续分析几个区域:
- 黄色,能直接求出来,就是
sum[row1 - 1, col1 - 1](为什么减⼀?因为要剔除掉row这一行和col这一列) - 绿色,直接求不好求,但是和黄色拼起来,正好是
sum表内sum[row1 - 1][col2]的数据; - 同理,蓝色不好求,但是 蓝 + 黄 =
sum[row2][col1 - 1]; - 再看看整个面积,好求嘛?非常好求,正好是
sum[row2][col2]; - 那么,红色就 = 整个面积 - 黄 - 绿 - 蓝,但是绿蓝不好求,我们可以这样减:整个面积 -(绿+ 黄 )-(蓝 + 黄),这样相当于多减去了⼀个黄,再加上即可
综上所述:红 = 整个面积 - (绿 + 黄)- (蓝 + 黄)+ 黄,从而可得红色区域内的元素总和为:
sum[row2][col2] - sum[row2][col1 - 1] - sum[row1 - 1][col2] + sum[row1 -1][col1 - 1]
C++算法代码:
cpp
#include <iostream>
#include<vector>
using namespace std;
int main() {
//1.输入数据
int n=0,m=0,q=0;
cin>>n>>m>>q;
vector<vector<int>> arr(n+1,vector<int>(m+1));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
cin>>arr[i][j];
//2.预处理
vector<vector<long long>> dp(n+1,vector<long long>(m+1));
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
dp[i][j]=dp[i-1][j]+dp[i][j-1]+arr[i][j]-dp[i-1][j-1];
//3.使用前缀和
int x1=0,y1=0,x2=0,y2=0;
while(q--)
{
cin>>x1>>y1>>x2>>y2;
cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<'\n';
}
return 0;
}
// 64 位输出请用 printf("%lld")算法总结&&笔记展示:
笔记字有点丑,大家见谅:
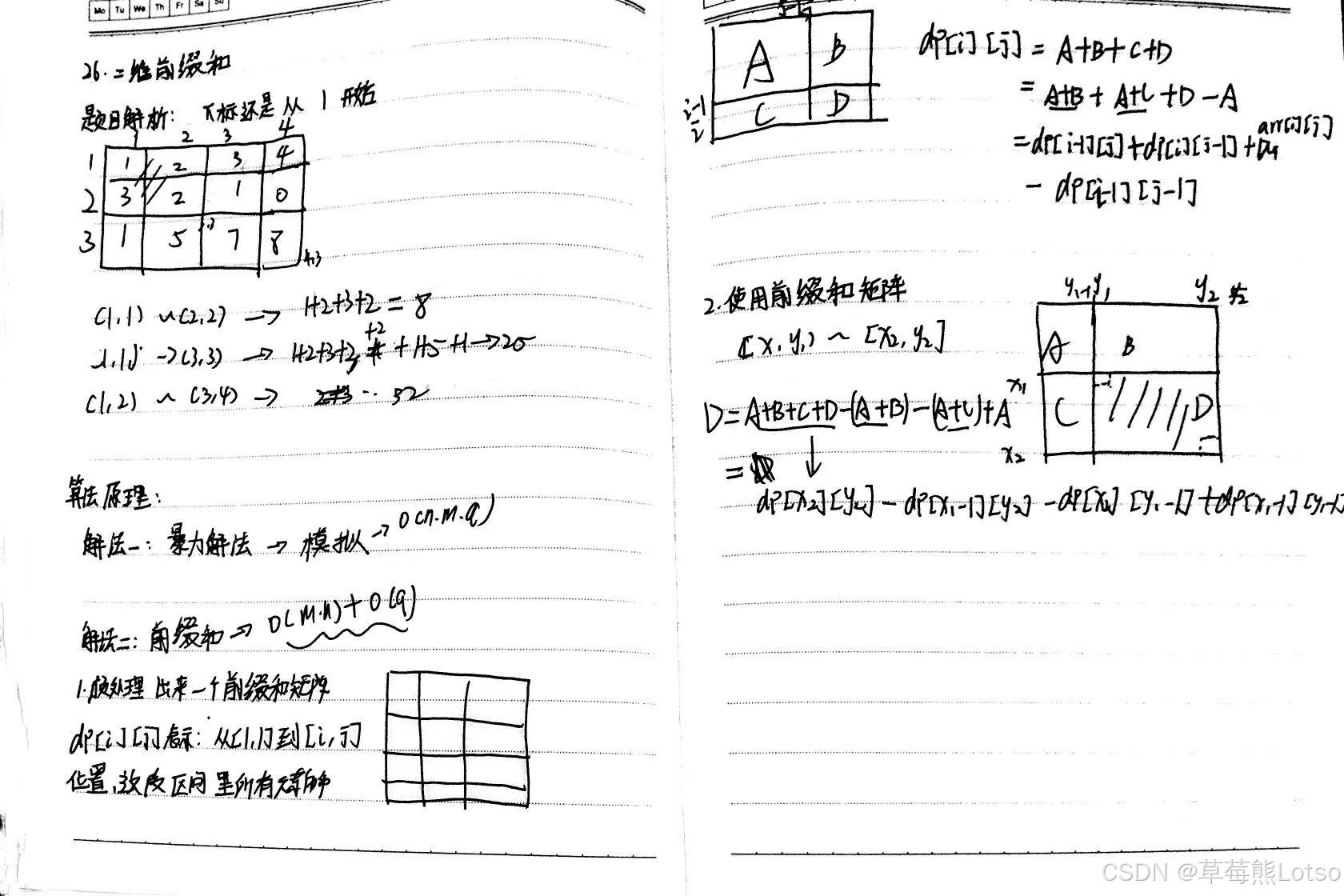
结尾:
html
🍓 我是草莓熊 Lotso!若这篇技术干货帮你打通了学习中的卡点:
👀 【关注】跟我一起深耕技术领域,从基础到进阶,见证每一次成长
❤️ 【点赞】让优质内容被更多人看见,让知识传递更有力量
⭐ 【收藏】把核心知识点、实战技巧存好,需要时直接查、随时用
💬 【评论】分享你的经验或疑问(比如曾踩过的技术坑?),一起交流避坑
🗳️ 【投票】用你的选择助力社区内容方向,告诉大家哪个技术点最该重点拆解
技术之路难免有困惑,但同行的人会让前进更有方向~愿我们都能在自己专注的领域里,一步步靠近心中的技术目标!结语:本文介绍了前缀和算法的核心思想及实现方式。通过预处理构建前缀和数组dp,其中dp[i]表示区间[1,i]内所有元素的和,利用递推公式dp[i]=dp[i-1]+arr[i]快速计算。查询区间[l,r]的和时,只需计算dp[r]-dp[l-1]即可高效获取结果。文章以C++代码演示了该算法的应用,并附有手写笔记说明。前缀和算法适用于频繁区间求和场景,能显著提升计算效率。
✨把这些内容吃透超牛的!放松下吧✨ ʕ˘ᴥ˘ʔ づきらど
