「用Python来学微积分」18. 微分

微分是微积分中最核心的概念之一，它描述了函数在某一点附近的局部线性行为。本文将基于教材内容，详细解析微分的定义、性质、几何意义以及实际应用。

一、微分的数学定义：精确描述变化率

1.1 从函数增量到微分

设函数 y=f(x)y = f(x)y=f(x) 在点 x0x_0x0 的某个邻域内有定义，当自变量 xxx 在 x0x_0x0 处有增量 Δx\Delta xΔx 时，函数相应的增量为：

Δy=f(x0+Δx)−f(x0)\Delta y = f(x_0 + \Delta x) - f(x_0)Δy=f(x0+Δx)−f(x0)

关键观察 ：对于许多函数，当 Δx\Delta xΔx 很小时，Δy\Delta yΔy 可以近似表示为 Δx\Delta xΔx 的线性函数。

1.2 微分的严格定义

如果存在不依赖于 Δx\Delta xΔx 的常数 AAA，使得：

Δy=AΔx+o(Δx)\Delta y = A\Delta x + o(\Delta x)Δy=AΔx+o(Δx)

其中 o(Δx)o(\Delta x)o(Δx) 是比 Δx\Delta xΔx 高阶的无穷小（即 lim⁡Δx→0o(Δx)Δx=0\lim_{\Delta x \to 0} \frac{o(\Delta x)}{\Delta x} = 0limΔx→0Δxo(Δx)=0），则称函数 y=f(x)y = f(x)y=f(x) 在点 x0x_0x0 处可微。

此时，AΔxA\Delta xAΔx 称为函数在点 x0x_0x0 处的微分，记作：

dy=AΔx或df(x0)=AΔxdy = A\Delta x \quad \text{或} \quad df(x_0) = A\Delta xdy=AΔx或df(x0)=AΔx

1.3 Python验证微分定义

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

def demonstrate_differential_definition():
    """演示微分定义：Δy = AΔx + o(Δx)"""
    
    # 定义函数 f(x) = x²
    f = lambda x: x**2
    x0 = 2
    A = 2*x0  # 对于f(x)=x²，f'(x)=2x，所以A=2x0=4
    
    print("微分定义验证: f(x) = x², x₀ = 2")
    print("=" * 60)
    print("Δx\t\tΔy\t\tAΔx\t\to(Δx)\t\to(Δx)/Δx")
    
    # 测试不同大小的Δx
    delta_x_values = [0.5, 0.1, 0.01, 0.001, 0.0001]
    
    for dx in delta_x_values:
        delta_y = f(x0 + dx) - f(x0)  # 实际增量
        A_dx = A * dx                 # 线性主部（微分）
        o_dx = delta_y - A_dx         # 高阶无穷小
        ratio = o_dx / dx if dx != 0 else 0
        
        print(f"{dx:.4f}\t{delta_y:.6f}\t{A_dx:.6f}\t{o_dx:.8f}\t{ratio:.8f}")

demonstrate_differential_definition()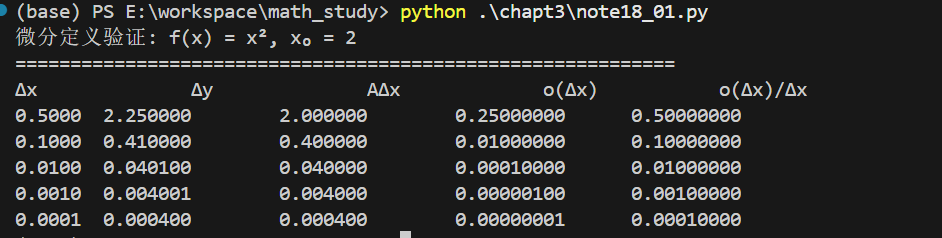

运行结果分析：

当 Δx\Delta xΔx 越来越小时，o(Δx)/Δxo(\Delta x)/\Delta xo(Δx)/Δx 趋近于 0
这验证了 o(Δx)o(\Delta x)o(Δx) 确实是比 Δx\Delta xΔx 高阶的无穷小
Δy\Delta yΔy 确实可以表示为 AΔxA\Delta xAΔx 加上一个高阶无穷小项

二、可微与可导的等价关系

2.1 重要定理

定理：函数 f(x)f(x)f(x) 在点 x0x_0x0 处可微的充分必要条件 是 f(x)f(x)f(x) 在 x0x_0x0 处可导，且：

df(x0)=f′(x0)dxdf(x_0) = f'(x_0)dxdf(x0)=f′(x0)dx

其中 dx=Δxdx = \Delta xdx=Δx。

2.2 证明思路

必要性（可微⇒可导） ：如果 f(x)f(x)f(x) 在 x0x_0x0 处可微，则 Δy=AΔx+o(Δx)\Delta y = A\Delta x + o(\Delta x)Δy=AΔx+o(Δx)，于是：

lim⁡Δx→0ΔyΔx=lim⁡Δx→0(A+o(Δx)Δx)=A\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \left(A + \frac{o(\Delta x)}{\Delta x}\right) = AΔx→0limΔxΔy=Δx→0lim(A+Δxo(Δx))=A

所以 f′(x0)=Af'(x_0) = Af′(x0)=A，函数可导。

充分性（可导⇒可微） ：如果 f(x)f(x)f(x) 在 x0x_0x0 处可导，则：

lim⁡Δx→0ΔyΔx=f′(x0)\lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f'(x_0)Δx→0limΔxΔy=f′(x0)

根据极限定义，存在 α\alphaα 满足 lim⁡Δx→0α=0\lim_{\Delta x \to 0} \alpha = 0limΔx→0α=0，使得：

ΔyΔx=f′(x0)+α\frac{\Delta y}{\Delta x} = f'(x_0) + \alphaΔxΔy=f′(x0)+α

所以 Δy=f′(x0)Δx+αΔx\Delta y = f'(x_0)\Delta x + \alpha\Delta xΔy=f′(x0)Δx+αΔx，其中 αΔx=o(Δx)\alpha\Delta x = o(\Delta x)αΔx=o(Δx)。

2.3 Python验证等价关系

python 复制代码

def verify_equivalence():
    """验证可微与可导的等价性"""
    
    # 测试多个函数
    test_functions = [
        ("x²", lambda x: x**2, lambda x: 2*x),
        ("sin(x)", np.sin, np.cos),
        ("e^x", np.exp, np.exp),
        ("ln(x)", lambda x: np.log(x) if x > 0 else np.nan, lambda x: 1/x if x > 0 else np.nan)
    ]
    
    x0 = 1
    dx = 0.001
    
    print("可微与可导等价性验证")
    print("=" * 50)
    
    for name, func, deriv in test_functions:
        # 通过导数计算微分
        dy_through_derivative = deriv(x0) * dx
        
        # 通过定义计算微分
        delta_y = func(x0 + dx) - func(x0)
        # 对于可微函数，A = f'(x0)
        dy_through_definition = deriv(x0) * dx
        
        error = abs(dy_through_derivative - dy_through_definition)
        
        print(f"{name}:")
        print(f"  通过导数: dy = f'({x0})·dx = {deriv(x0):.4f} × {dx} = {dy_through_derivative:.6f}")
        print(f"  通过定义: dy = A·dx = {dy_through_definition:.6f}")
        print(f"  误差: {error:.10f}")
        print()

verify_equivalence()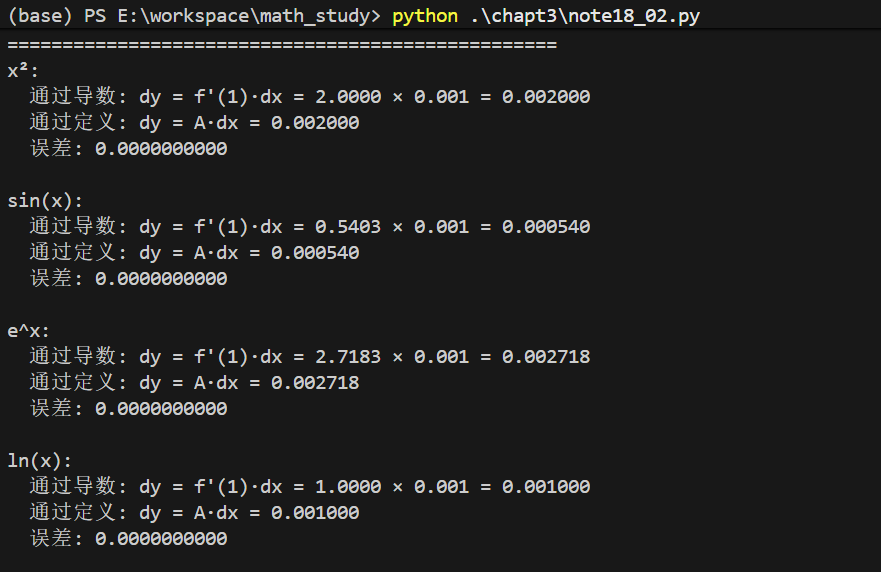

三、微分的几何意义：切线与局部线性化

3.1 几何解释

微分 dy=f′(x0)dxdy = f'(x_0)dxdy=f′(x0)dx 的几何意义是：它表示曲线 y=f(x)y = f(x)y=f(x) 在点 (x0,f(x0))(x_0, f(x_0))(x0,f(x0)) 处切线的纵坐标改变量。

具体来说：

曲线在点 P(x0,f(x0))P(x_0, f(x_0))P(x0,f(x0)) 处的切线方程为：y=f(x0)+f′(x0)(x−x0)y = f(x_0) + f'(x_0)(x - x_0)y=f(x0)+f′(x0)(x−x0)
当 xxx 从 x0x_0x0 变化到 x0+dxx_0 + dxx0+dx 时：
- 曲线的实际纵坐标变化：Δy=f(x0+dx)−f(x0)\Delta y = f(x_0 + dx) - f(x_0)Δy=f(x0+dx)−f(x0)
- 切线的纵坐标变化：dy=f′(x0)dxdy = f'(x_0)dxdy=f′(x0)dx

3.2 Python可视化几何意义

python 复制代码

def visualize_geometric_meaning():
    """可视化微分的几何意义"""
    
    # 定义函数和点
    f = lambda x: 0.5*x**3 - x**2 + 2
    x0 = 1.5
    derivative = 1.5*x0**2 - 2*x0  # f'(x) = 1.5x² - 2x
    
    # 生成数据
    x = np.linspace(0.5, 2.5, 100)
    y_curve = f(x)
    y_tangent = f(x0) + derivative * (x - x0)  # 切线方程
    
    # 选择增量
    dx = 0.3
    x1 = x0 + dx
    
    plt.figure(figsize=(12, 10))
    
    # 主图：完整视图
    plt.subplot(2, 1, 1)
    plt.plot(x, y_curve, 'b-', linewidth=3, label='y = f(x)')
    plt.plot(x, y_tangent, 'r--', linewidth=2, label=f'切线 (斜率={derivative:.2f})')
    
    # 标记关键点
    plt.scatter([x0, x1], [f(x0), f(x1)], color='red', s=100, zorder=5)
    plt.scatter([x1], [f(x0) + derivative*dx], color='green', s=100, zorder=5)
    
    # 绘制重要线段
    plt.plot([x0, x1], [f(x0), f(x0)], 'g-', linewidth=2, label='dx = Δx')  # dx
    plt.plot([x1, x1], [f(x0), f(x1)], 'b-', linewidth=2, label='Δy')  # Δy
    plt.plot([x1, x1], [f(x0), f(x0) + derivative*dx], 'r-', linewidth=2, label='dy')  # dy
    
    # 标注点
    plt.annotate(f'P({x0:.1f}, {f(x0):.2f})', (x0, f(x0)), 
                xytext=(x0-0.3, f(x0)-0.4))
    plt.annotate(f'Q({x1:.1f}, {f(x1):.2f})', (x1, f(x1)), 
                xytext=(x1+0.1, f(x1)))
    plt.annotate(f'R({x1:.1f}, {f(x0)+derivative*dx:.2f})', 
                (x1, f(x0)+derivative*dx), xytext=(x1+0.1, f(x0)+derivative*dx-0.3))
    
    plt.title('微分的几何意义：dy是切线的纵坐标改变量')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()
    plt.grid(True, alpha=0.3)
    
    # 子图：局部放大
    plt.subplot(2, 1, 2)
    x_zoom = np.linspace(x0-0.2, x0+0.5, 100)
    y_curve_zoom = f(x_zoom)
    y_tangent_zoom = f(x0) + derivative * (x_zoom - x0)
    
    plt.plot(x_zoom, y_curve_zoom, 'b-', linewidth=3, label='f(x)')
    plt.plot(x_zoom, y_tangent_zoom, 'r--', linewidth=2, label='切线')
    
    # 突出显示微分dy
    plt.plot([x0, x1], [f(x0), f(x0) + derivative*dx], 'r-', linewidth=4, alpha=0.6, label='dy')
    plt.fill_between([x0, x1], [f(x0), f(x0)], 
                    [f(x0), f(x0) + derivative*dx], alpha=0.2, color='red')
    
    plt.title('局部放大：微分dy的几何意义')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()
    plt.grid(True, alpha=0.3)
    
    plt.tight_layout()
    plt.show()
    
    # 数值分析
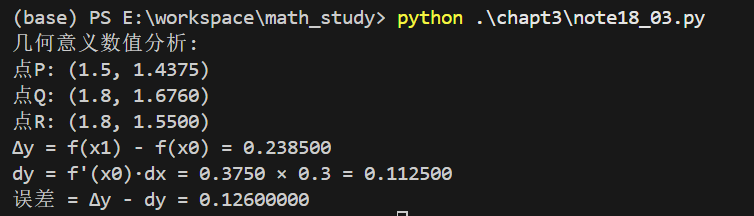
    print("几何意义数值分析:")
    print(f"点P: ({x0}, {f(x0):.4f})")
    print(f"点Q: ({x1}, {f(x1):.4f})")
    print(f"点R: ({x1}, {f(x0)+derivative*dx:.4f})")
    print(f"Δy = f(x1) - f(x0) = {f(x1)-f(x0):.6f}")
    print(f"dy = f'(x0)·dx = {derivative:.4f} × {dx} = {derivative*dx:.6f}")
    print(f"误差 = Δy - dy = {f(x1)-f(x0)-derivative*dx:.8f}")

visualize_geometric_meaning()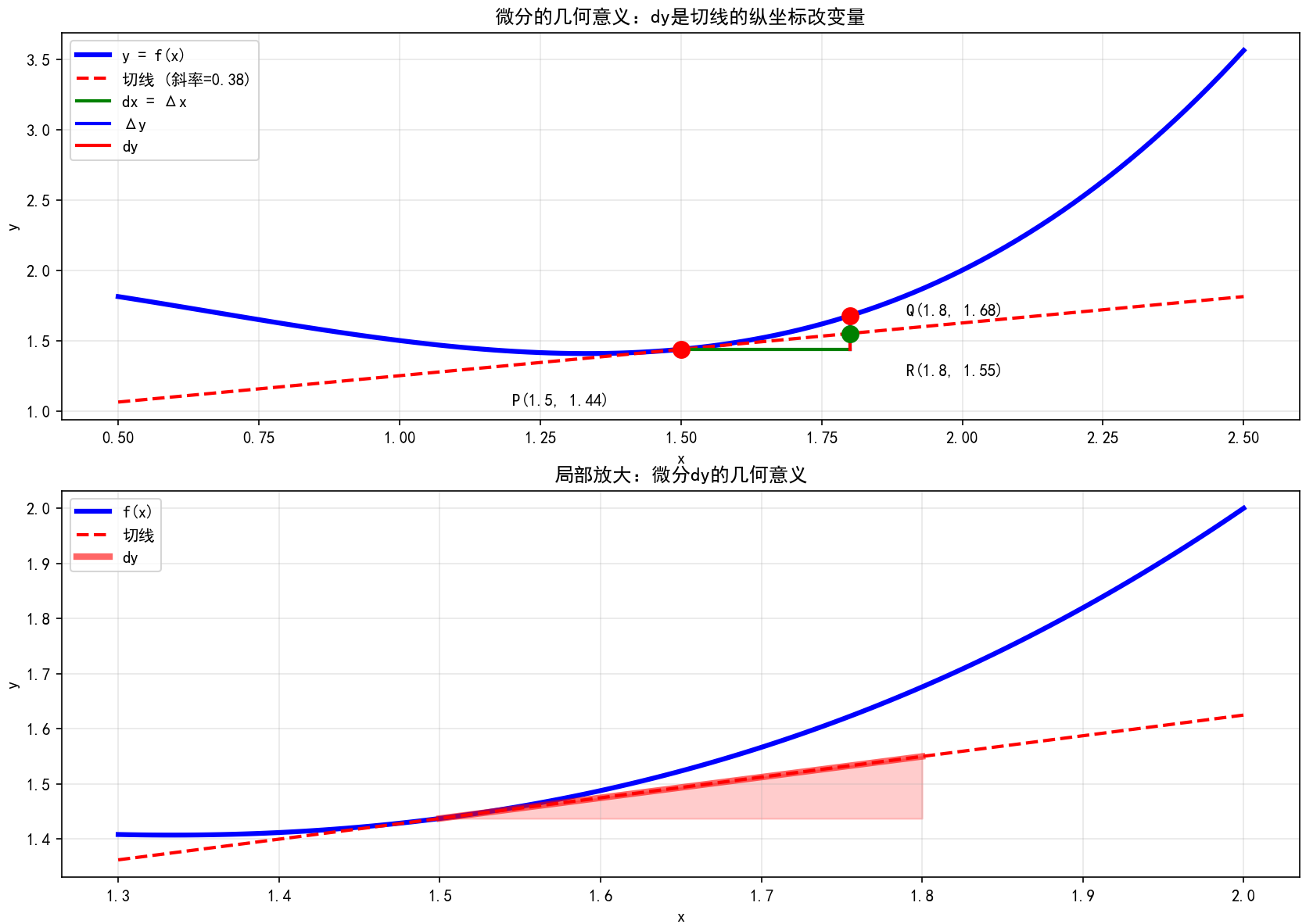

四、微分的应用：近似计算

4.1 近似计算公式

根据微分定义，当 ∣Δx∣|\Delta x|∣Δx∣ 很小时：

f(x0+Δx)≈f(x0)+f′(x0)Δxf(x_0 + \Delta x) \approx f(x_0) + f'(x_0)\Delta xf(x0+Δx)≈f(x0)+f′(x0)Δx

这个公式的几何解释是：在 x0x_0x0 附近，用切线（线性函数）来近似曲线（非线性函数）。

4.2 实际应用例子

例1 ：计算 9.01\sqrt{9.01}9.01 的近似值

令 f(x)=xf(x) = \sqrt{x}f(x)=x ，x0=9x_0 = 9x0=9，Δx=0.01\Delta x = 0.01Δx=0.01
f′(x)=12xf'(x) = \frac{1}{2\sqrt{x}}f′(x)=2x 1，f′(9)=16f'(9) = \frac{1}{6}f′(9)=61
9.01≈9+16×0.01=3+0.001667=3.001667\sqrt{9.01} \approx \sqrt{9} + \frac{1}{6} \times 0.01 = 3 + 0.001667 = 3.0016679.01 ≈9 +61×0.01=3+0.001667=3.001667

例2 ：计算 2.00252.002^52.0025 的近似值

令 f(x)=x5f(x) = x^5f(x)=x5，x0=2x_0 = 2x0=2，Δx=0.002\Delta x = 0.002Δx=0.002
f′(x)=5x4f'(x) = 5x^4f′(x)=5x4，f′(2)=5×16=80f'(2) = 5 \times 16 = 80f′(2)=5×16=80
2.0025≈25+80×0.002=32+0.16=32.162.002^5 \approx 2^5 + 80 \times 0.002 = 32 + 0.16 = 32.162.0025≈25+80×0.002=32+0.16=32.16

4.3 Python实现微分近似计算

python 复制代码

def differential_approximation_examples():
    """微分近似计算的实际例子"""
    
    examples = [
        {
            'name': '√9.01',
            'func': lambda x: np.sqrt(x),
            'deriv': lambda x: 1/(2*np.sqrt(x)),
            'x0': 9,
            'dx': 0.01,
            'exact': np.sqrt(9.01)
        },
        {
            'name': '2.002⁵',
            'func': lambda x: x**5,
            'deriv': lambda x: 5*x**4,
            'x0': 2,
            'dx': 0.002,
            'exact': 2.002**5
        },
        {
            'name': 'sin(0.1)',
            'func': np.sin,
            'deriv': np.cos,
            'x0': 0,
            'dx': 0.1,
            'exact': np.sin(0.1)
        },
        {
            'name': 'e^0.05',
            'func': np.exp,
            'deriv': np.exp,
            'x0': 0,
            'dx': 0.05,
            'exact': np.exp(0.05)
        }
    ]
    
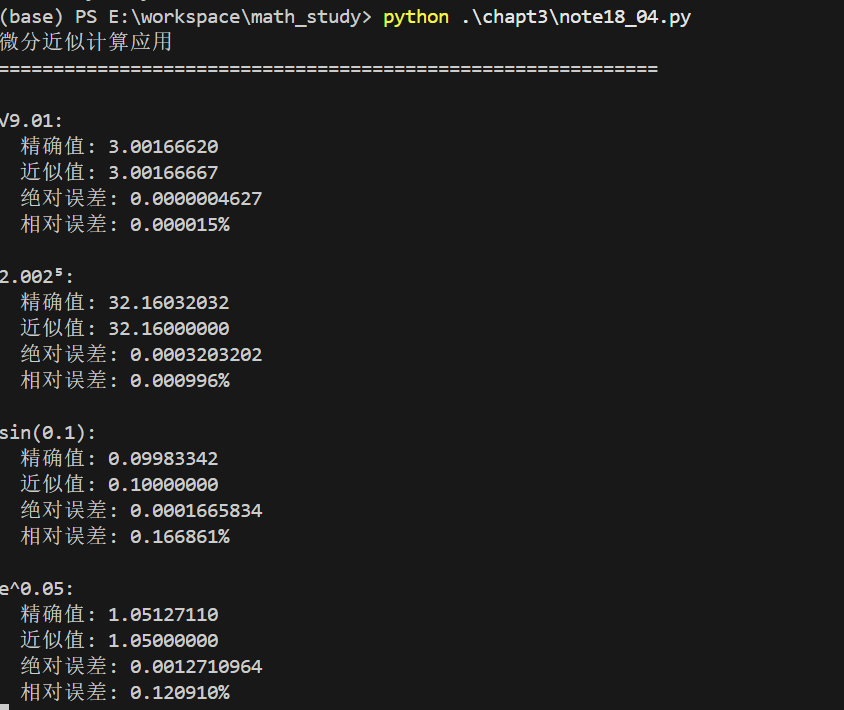
    print("微分近似计算应用")
    print("=" * 60)
    
    for example in examples:
        approx = example['func'](example['x0']) + example['deriv'](example['x0']) * example['dx']
        error = abs(example['exact'] - approx)
        relative_error = error / abs(example['exact']) * 100
        
        print(f"\n{example['name']}:")
        print(f"  精确值: {example['exact']:.8f}")
        print(f"  近似值: {approx:.8f}")
        print(f"  绝对误差: {error:.10f}")
        print(f"  相对误差: {relative_error:.6f}%")
    
    # 可视化近似效果
    plt.figure(figsize=(10, 6))
    
    # 以√x为例展示近似效果
    x_vals = np.linspace(8, 10, 100)
    y_exact = np.sqrt(x_vals)
    y_approx = np.sqrt(9) + (1/(2*np.sqrt(9))) * (x_vals - 9)
    
    plt.plot(x_vals, y_exact, 'b-', linewidth=2, label='精确值: √x')
    plt.plot(x_vals, y_approx, 'r--', linewidth=2, label='线性近似')
    plt.scatter([9.01], [np.sqrt(9.01)], color='green', s=100, zorder=5)
    
    plt.annotate('近似点 (9.01, 3.001667)', (9.01, np.sqrt(9.01)), 
                xytext=(9.2, 3.1))
    plt.title('微分近似计算: √9.01 的线性近似')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()
    plt.grid(True, alpha=0.3)
    plt.show()

differential_approximation_examples()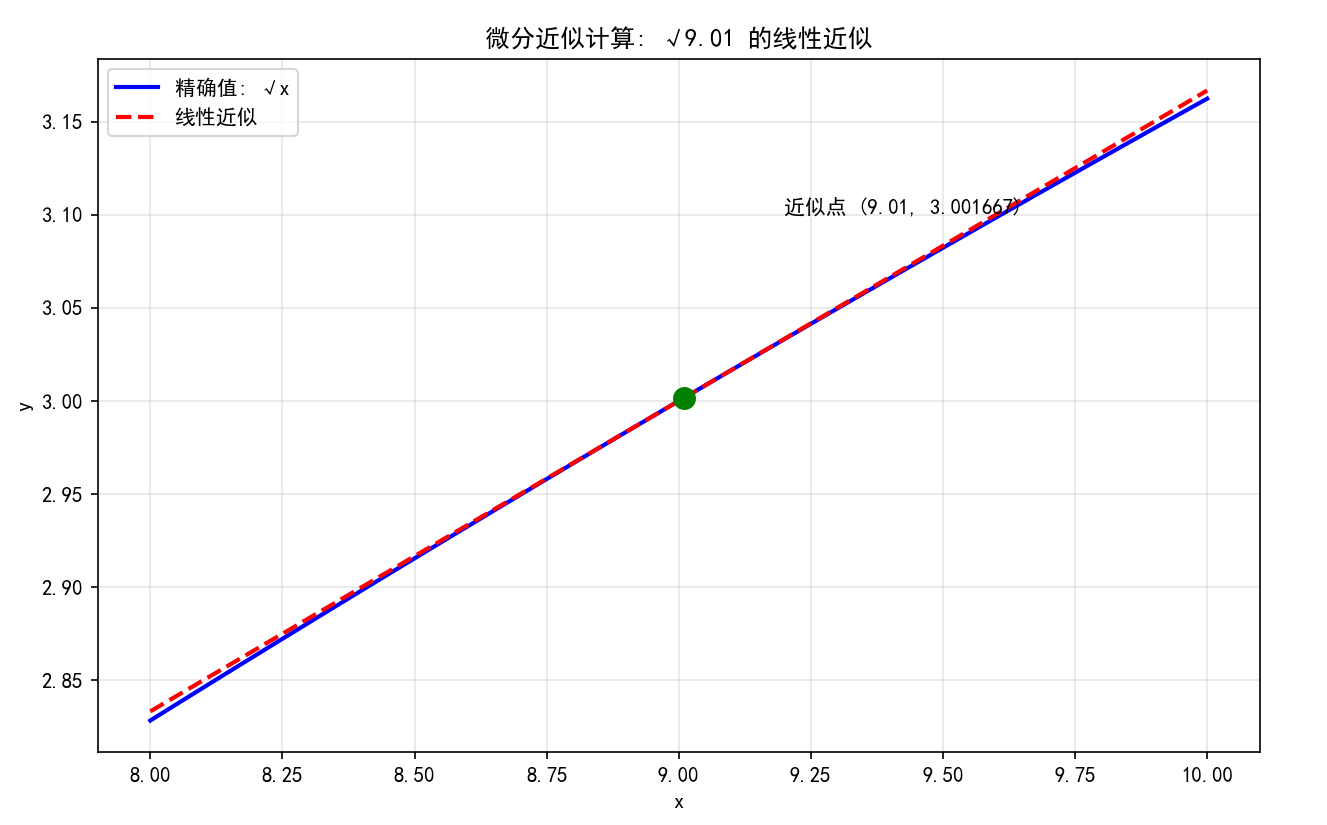

五、导数与微分的关系：微商概念

5.1 导数即微商

由微分定义 dy=f′(x)dxdy = f'(x)dxdy=f′(x)dx，可得：

f′(x)=dydxf'(x) = \frac{dy}{dx}f′(x)=dxdy

这意味着导数就是函数微分与自变量微分的商 ，因此导数也称为微商。

5.2 微分的形式不变性

对于复合函数 y=f(u)y = f(u)y=f(u)，u=g(x)u = g(x)u=g(x)，有：

dy=f′(u)dudy = f'(u)dudy=f′(u)du

无论 uuu 是自变量还是中间变量，微分形式保持不变。

六、总结与拓展

6.1 微分概念的核心要点

定义：Δy=AΔx+o(Δx)\Delta y = A\Delta x + o(\Delta x)Δy=AΔx+o(Δx)，其中 AΔxA\Delta xAΔx 是微分
与导数的关系 ：可微 ⇔ 可导，且 dy=f′(x)dxdy = f'(x)dxdy=f′(x)dx
几何意义：切线的纵坐标改变量
应用：局部线性近似，误差估计

6.2 微分在现实世界中的意义

微分提供了将复杂非线性问题局部线性化的工具，这在工程、物理、经济学等领域有广泛应用：

工程：材料应力分析、结构优化
物理：瞬时速度、加速度计算
经济学：边际成本、边际收益分析
机器学习：梯度下降算法优化

🔍 思考与讨论

概念理解：为什么说微分是"以直代曲"的数学实现？
实际应用：你能想到生活中哪些地方用到了微分近似的思想？
深入思考：微分与导数的关系如何体现了局部与整体的联系？

下节预告：在下一篇文章中，我们将学习导数的计算法则，包括基本初等函数的导数公式、四则运算法则、复合函数求导法则等，让你能够快速计算各种复杂函数的导数。

参考资料：

扈志明《微积分》教材

互动邀请：如果你对微分概念有独特的理解或在实际应用中遇到过有趣的问题，欢迎在评论区分享交流！