目录
为什么要使用红黑树?
二叉排序树BST在进行查找、最大值、最小值、插入等操作时,期望的时间复杂度是 O(logn) 。但是BST在极端情况下会出现斜树(退化成一条链表),BST的时间复杂度将会变成O(n)。为了保证BST的所有操作的时间复杂度为O(logn),就要想办法把一颗BST树的高度一直维持在logn。红黑树通过变色和旋转等操作,高度始终都维持在logn,从而确保查找、插入等操作的时间复杂度。
AVL与红黑树
AVL 树比红黑树更加平衡,但AVL树在插入和删除的时候会存在大量的旋转操作,影响效率。所以,当程序需要频繁的插入和删除操作,应该选择性能更好的红黑树;当然,如果程序中涉及的插入和删除操作并不频繁,而是查找操作相对更频繁,那么就优先选择 AVL 树进行实现。
什么是红黑树?
红黑树是一种自平衡的二叉查找树,它通过下列规则,保持二叉树的平衡性。
- 任何一个结点都有颜色,黑色或者红色;
- 根结点是黑色的;
- 父子结点之间不能出现两个连续的红色结点(每个红色节点的两个子节点都是黑色);
- 任何一个结点向下遍历到叶子结点,所经过的黑结点个数必须相等(相同的黑色高度);
- 每个叶子结点都是黑色的空结点(NIL 结点);
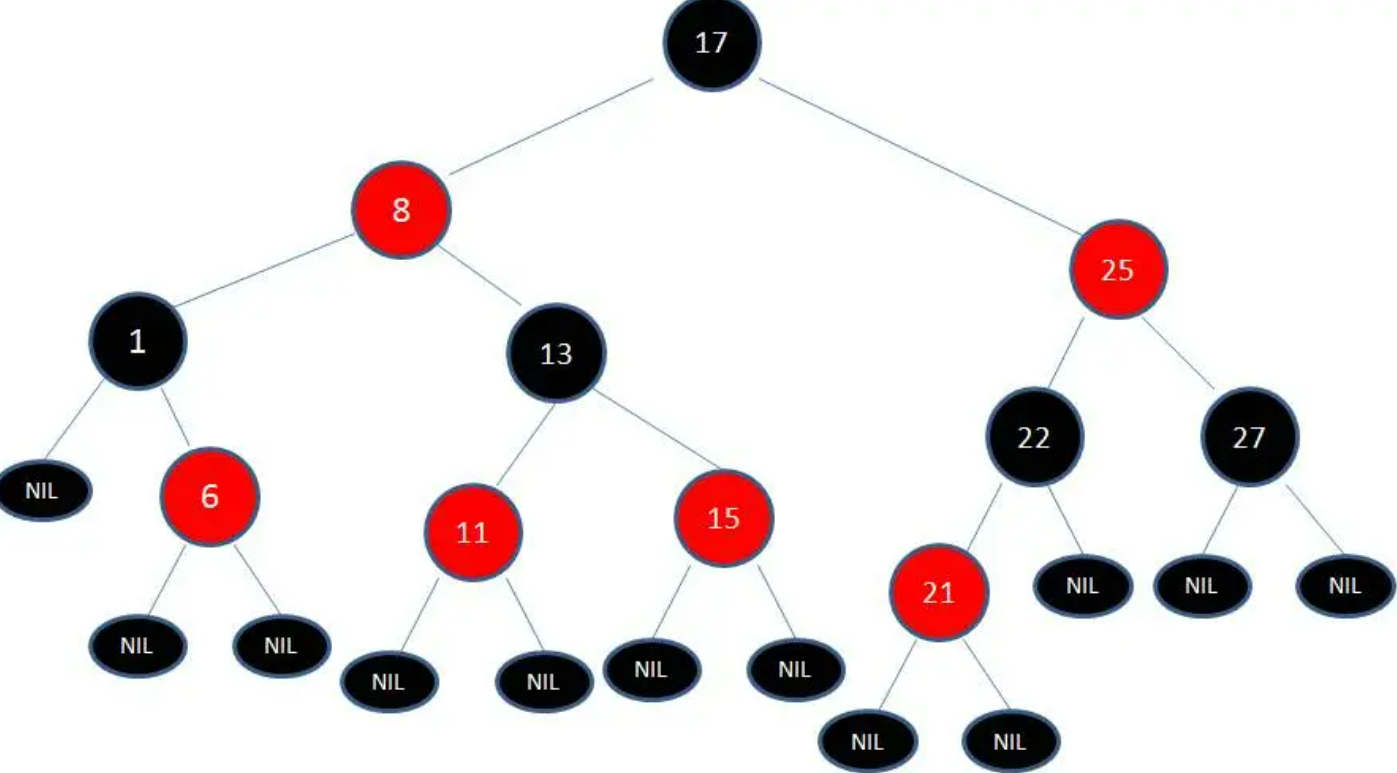
这就是一棵典型的红黑树,分析如下:
树中的每个结点的颜色要么是黑色,要么是红色;
根结点 13 为黑色结点;
树中不存在两个相邻的红色结点,比如:结点 17 为红色结点,其父亲节点 13 与两个孩子结点15和25就一定是黑色,而不能是红色;
从结点到其后代的 NIL 结点 的每条路径上具有相同数目的黑色结点,比如:根结点 13 到其左子树的 NIL 结点 包含三个黑色结点,到其右子树所有的 NIL 结点也包含三个黑色结点。
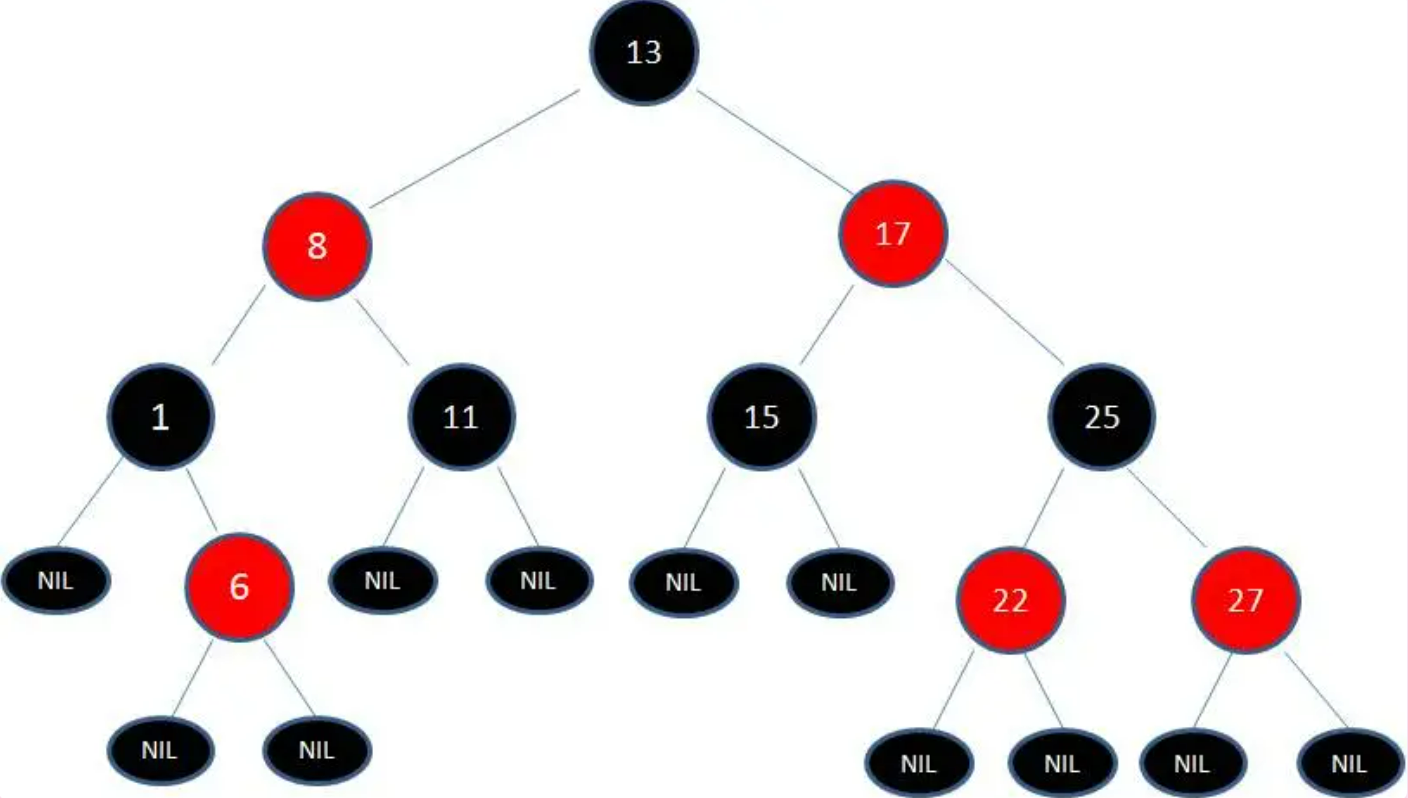
红黑树结点类参考实现:
java
class Node<T>{
public T value;
public Node<T> parent;
public boolean isRed;
public Node<T> left;
public Node<T> right;
}红黑树的平衡性
向红黑树插入值为14的新结点,由于父结点15是黑色结点,因此这种情况并不会破坏红黑树的规则,无需做任何调整。
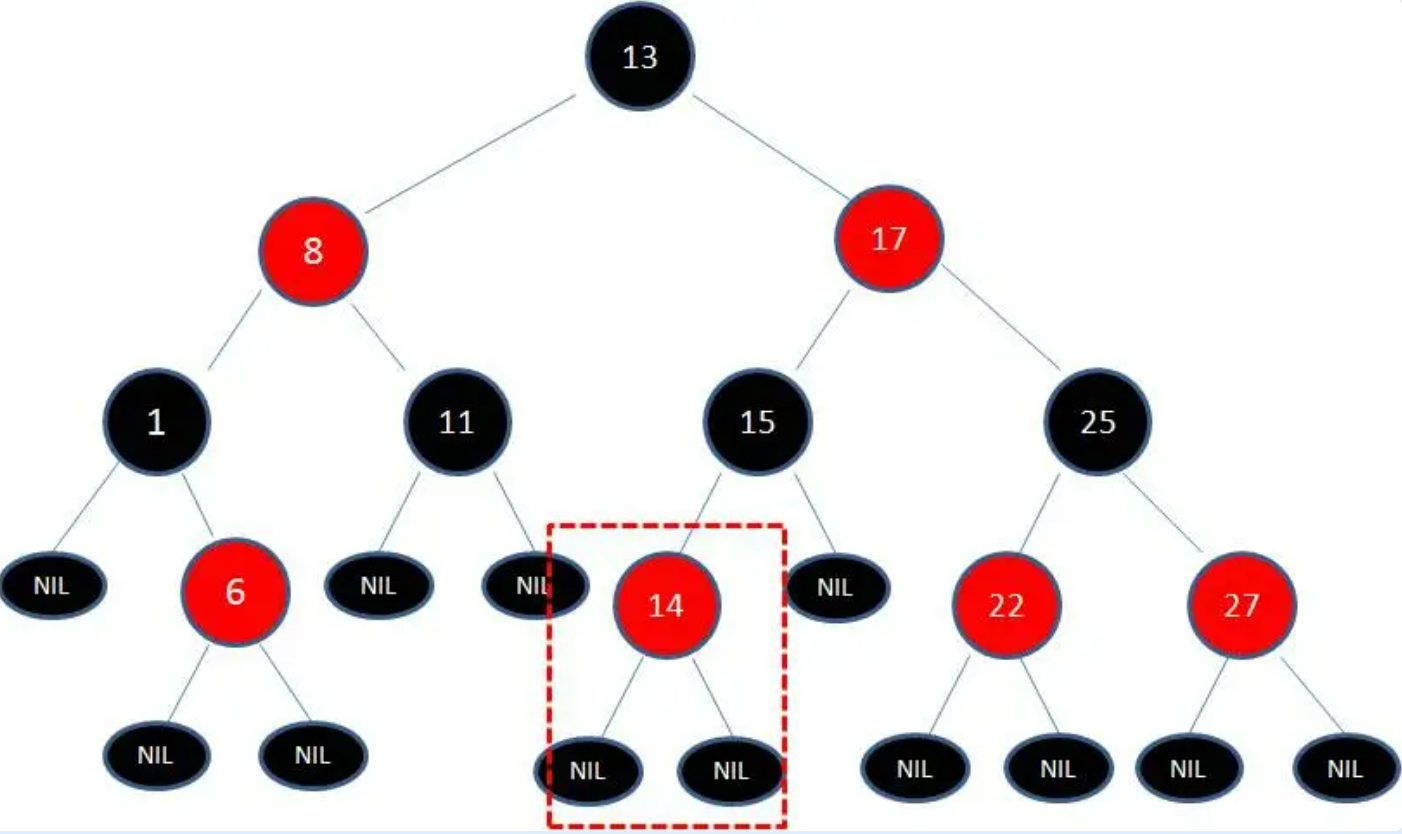
向红黑树插入值为21的新节点,由于父节点22是红色节点,因此这种情况打破了红黑树的规则3(每个红色节点的两个子节点都是黑色),必须进行调整,使之重新符合红黑树的规则。
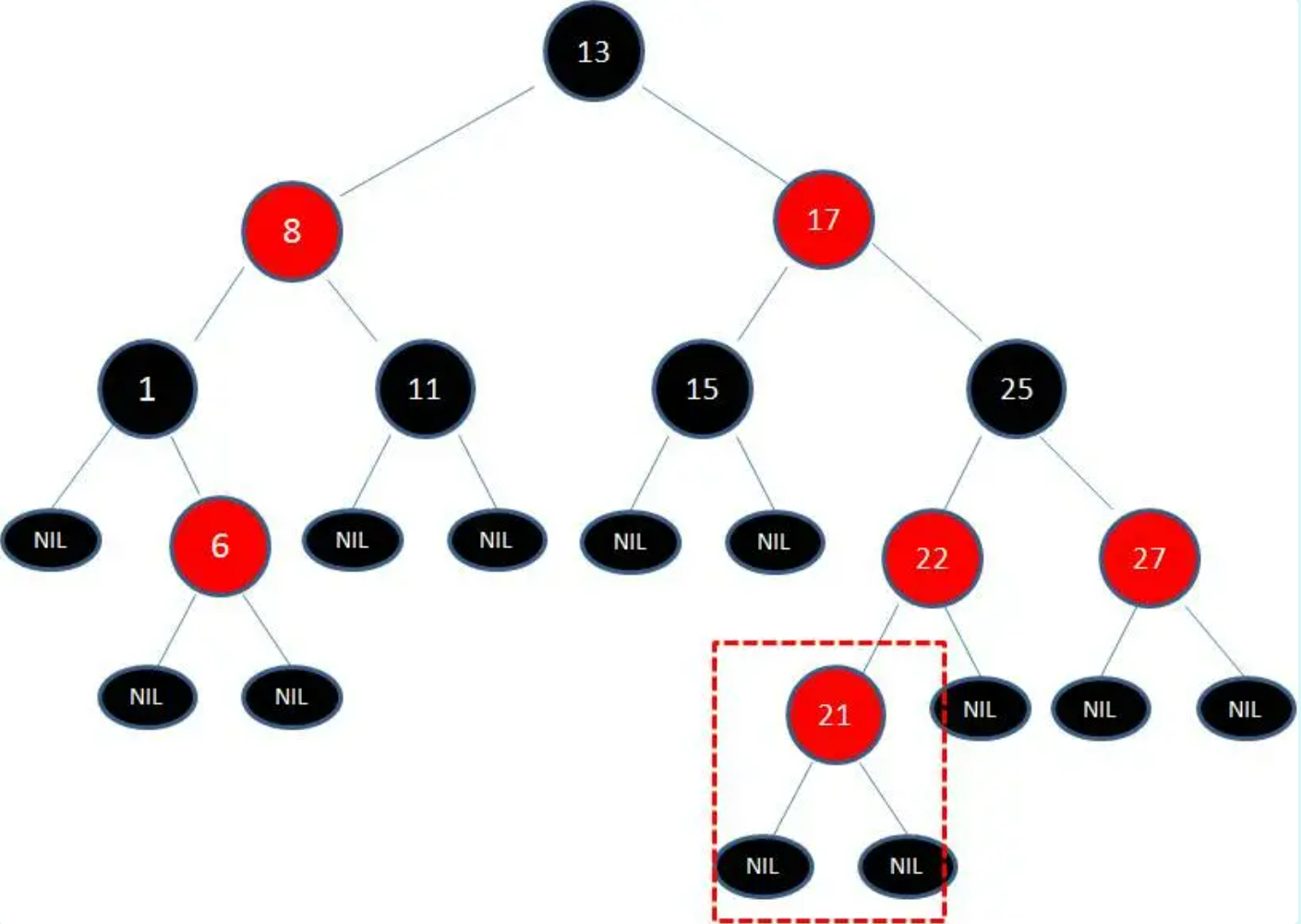
红黑树的调整
当红黑树在添加元素后,平衡性被破坏时,就需要进行调整,来保持符合红黑树的规则。调整的方法有两种:变色 和旋转。旋转又分为两种形式:左旋转和右旋转。
添加的新元素默认为红色,因为如果插入节点是黑色,就一定会违背每条查找线上黑色节点个数一致的规则,插入红色,就可能不需要变色或者旋转,所以新插入的节点颜色都是红色。
变色
为了重新符合红黑树的规则,尝试把红色节点变为黑色,或者把黑色节点变为红色。
红黑树中的根结点为25的子树中,由于添加新结点21后,导致节点21和节点22连续出现了红色,不符合规则3(每个红色节点的两个子节点都是黑色),所以把节点22从红色变成黑色。
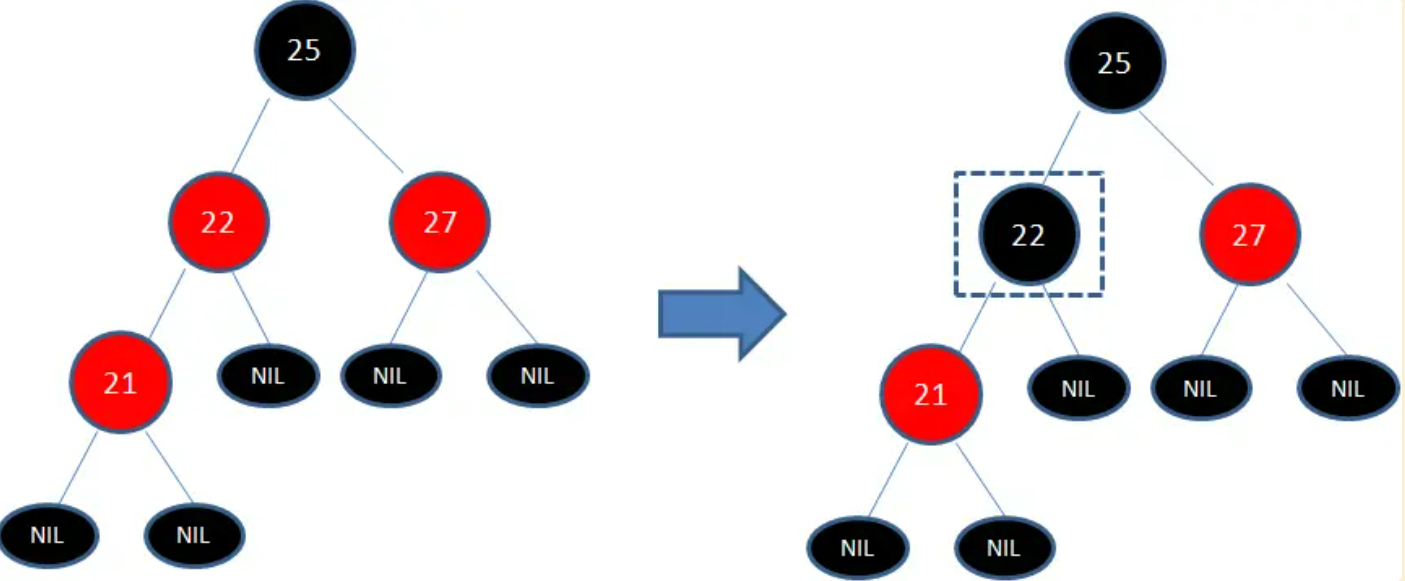
但是,因为的黑色节点22打破了红黑树的规则4(相同的黑色高度),所以发生连锁反应,需要继续把节点25从黑色变成红色。
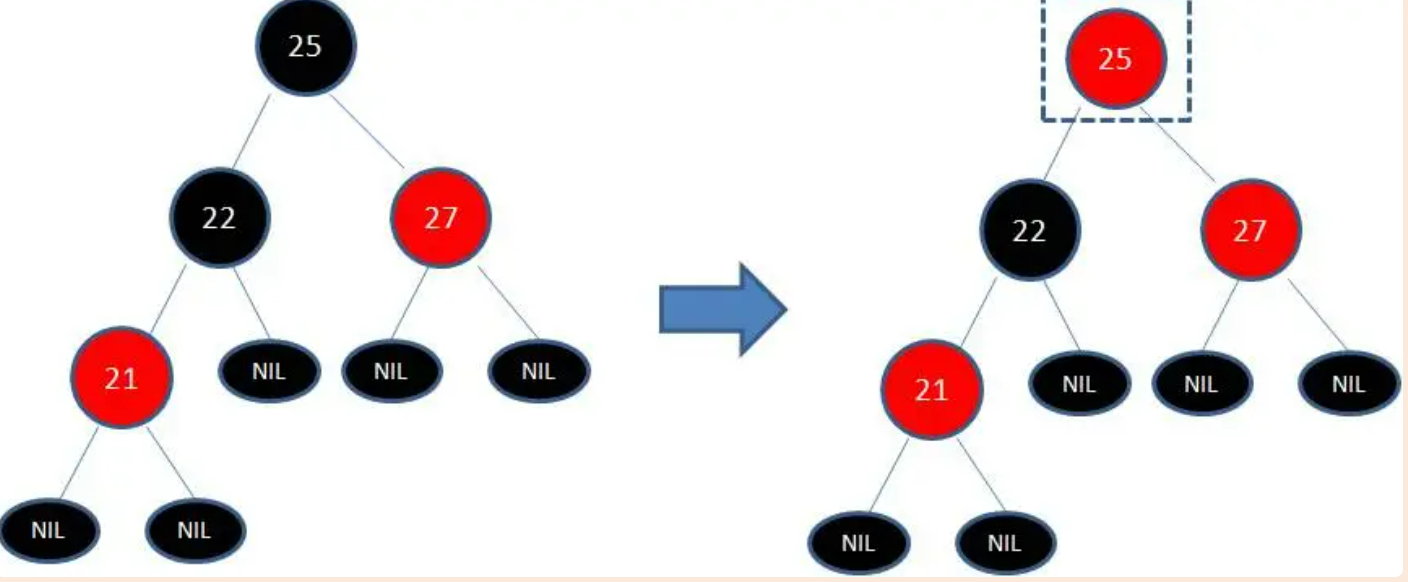
但是,因为节点25和节点27又形成了两个连续的红色节点,需要继续把节点27从红色变成黑色。
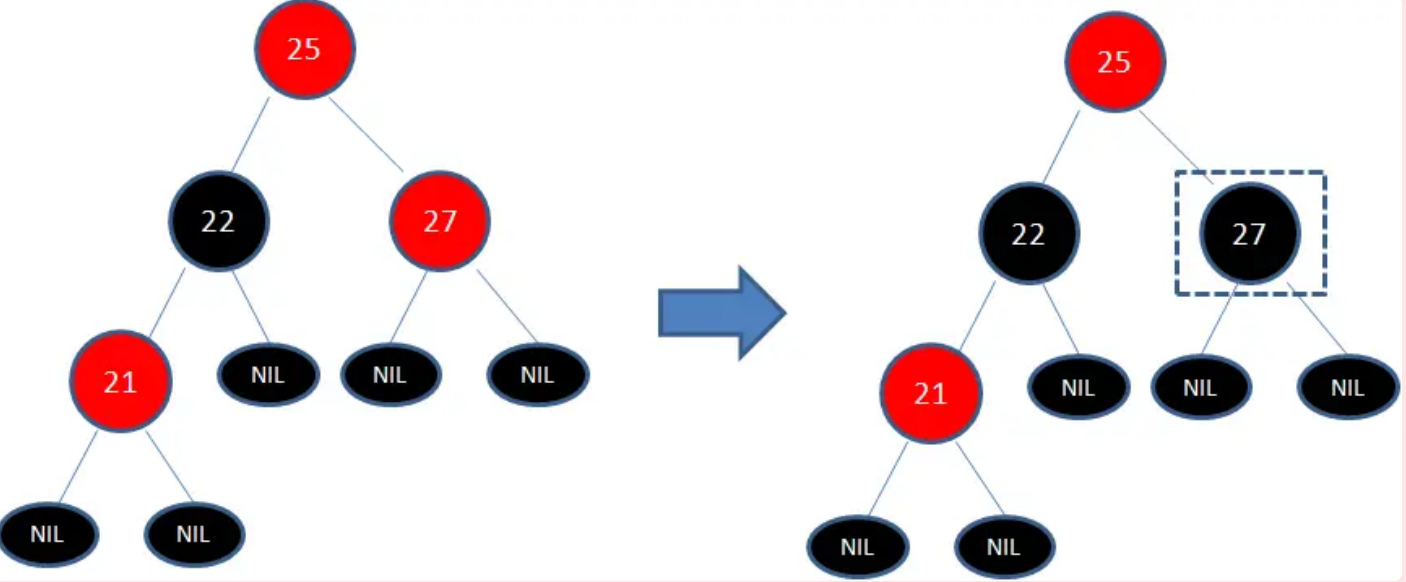
旋转
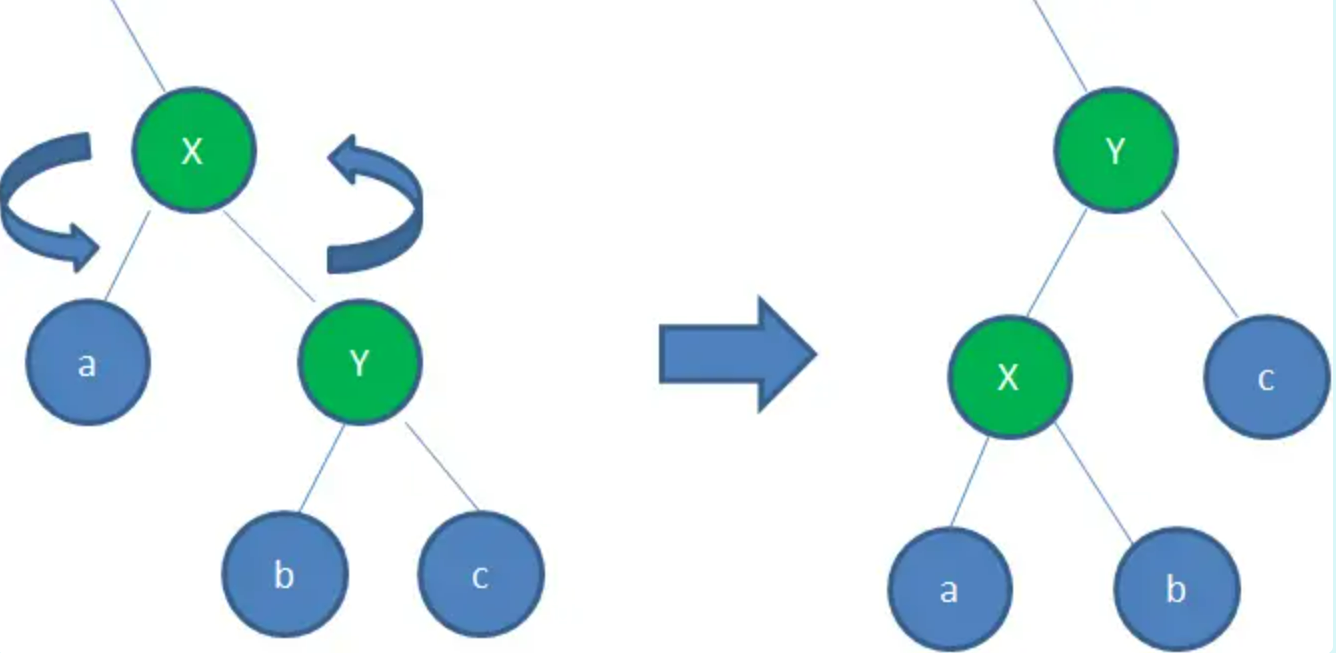
左旋转
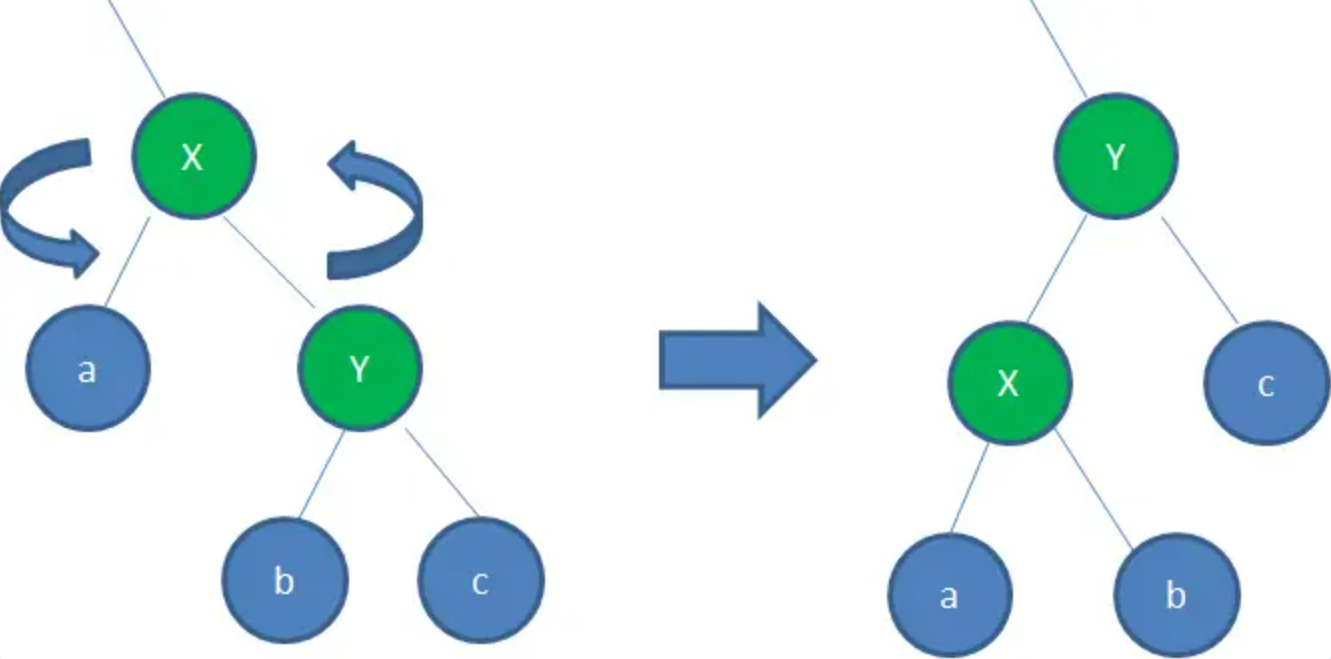
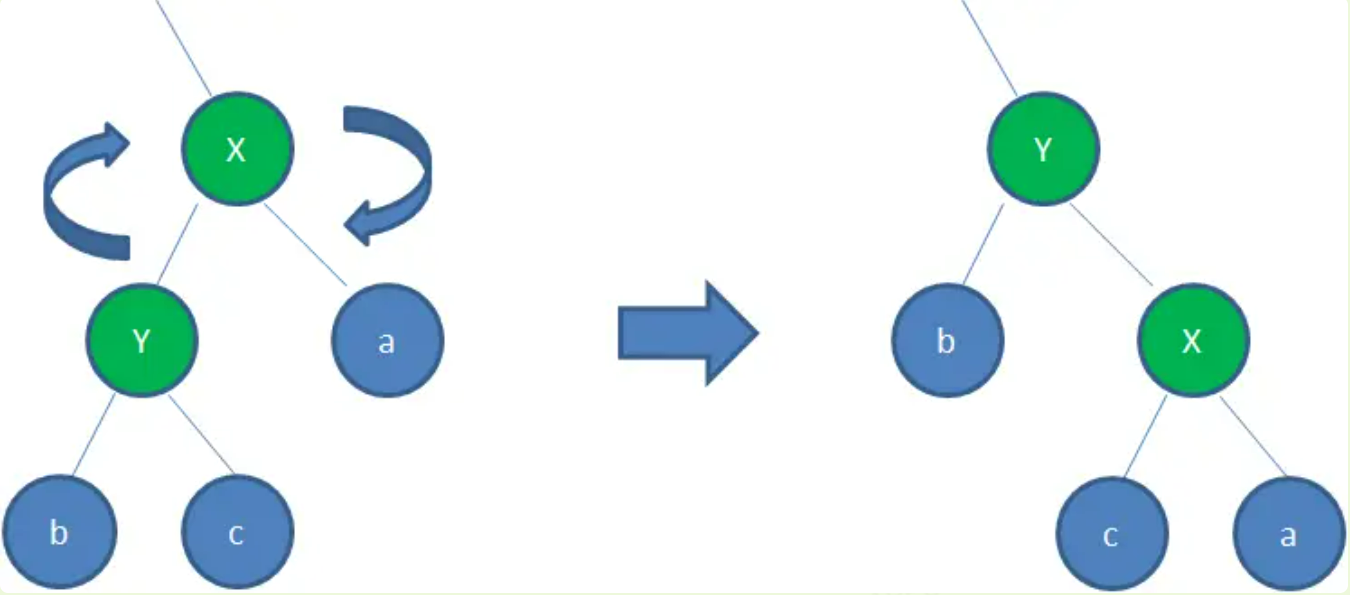
左旋转:逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。
例如:右孩子Y取代了父节点X的位置,而X变成了自己的左孩子。
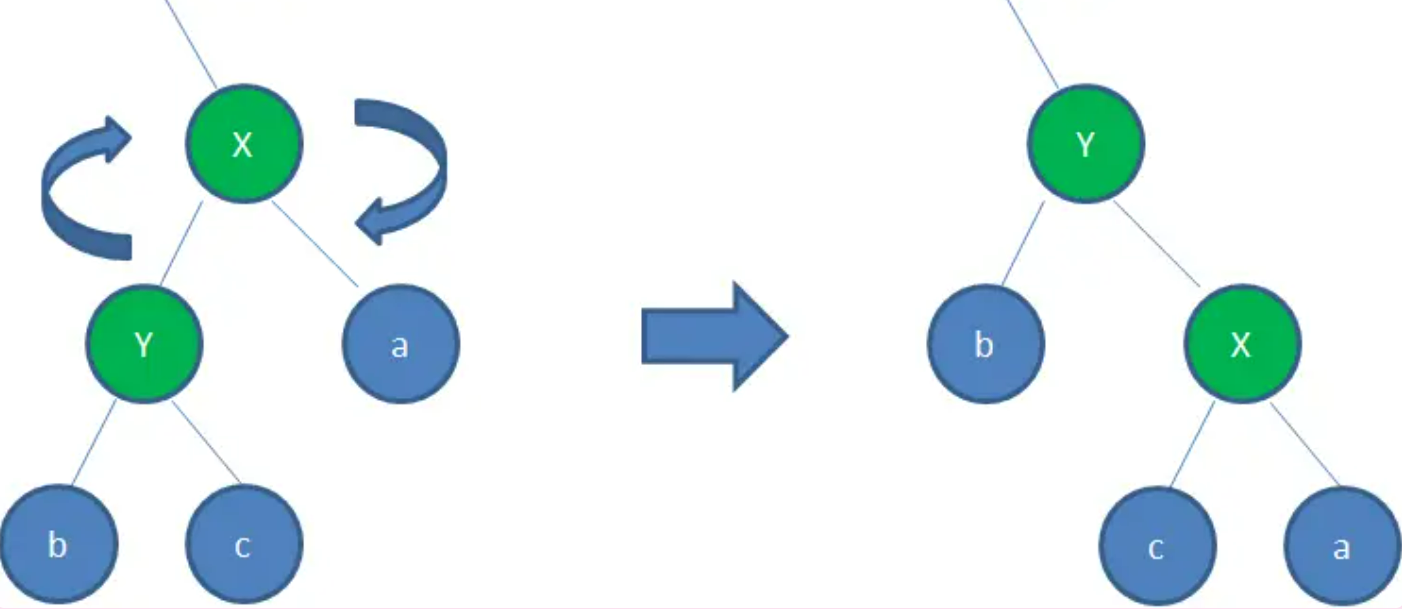
右旋转
右旋转:顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。
例如:左孩子Y取代了X的位置,而X变成了自己的右孩子。
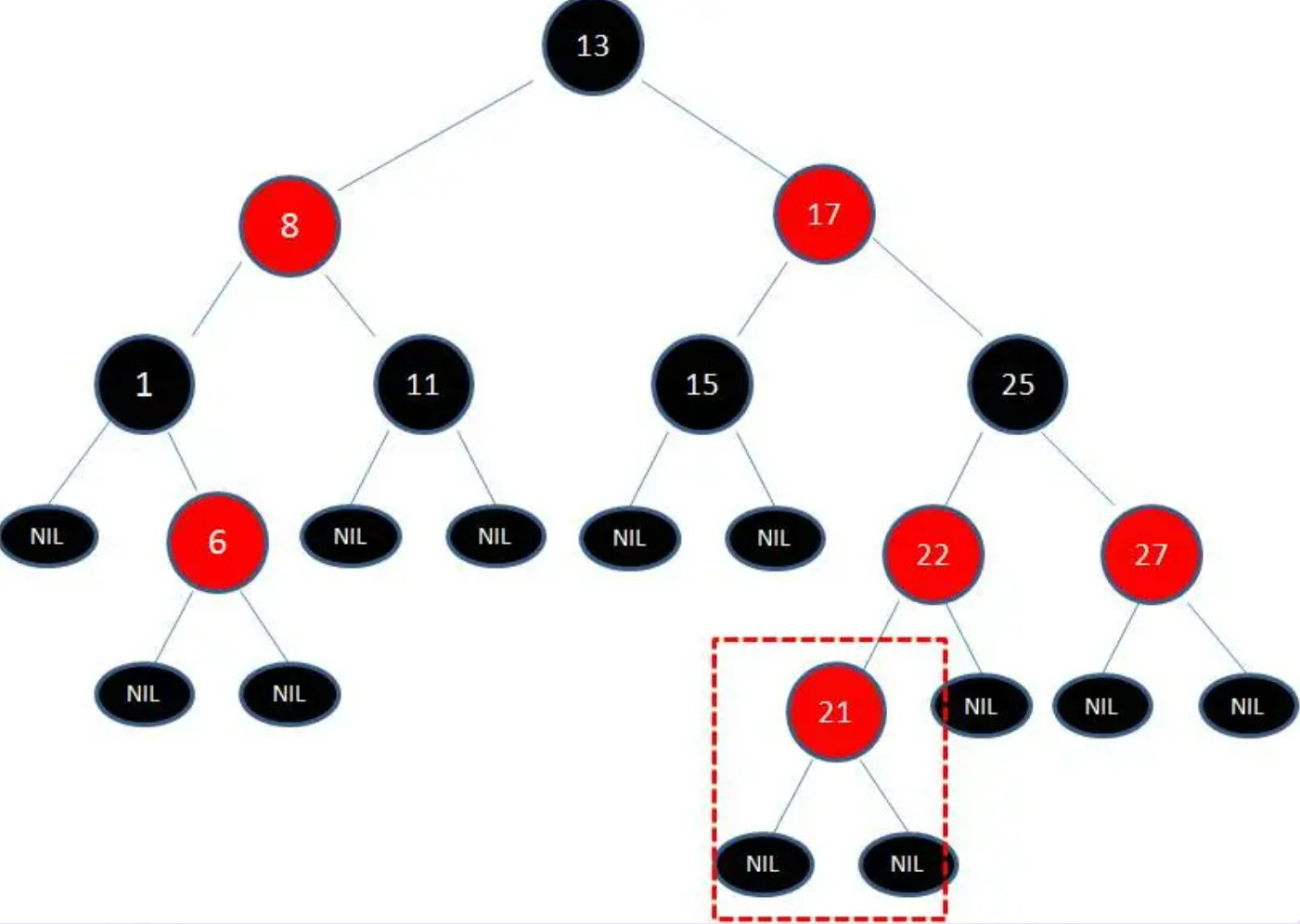
变色或旋转的案例
向红黑树插入值为21的新节点,由于父节点22是红色节点,因此这种情况打破了红黑树的规则3(每个红色节点的两个子节点都是黑色),需要进行调整。
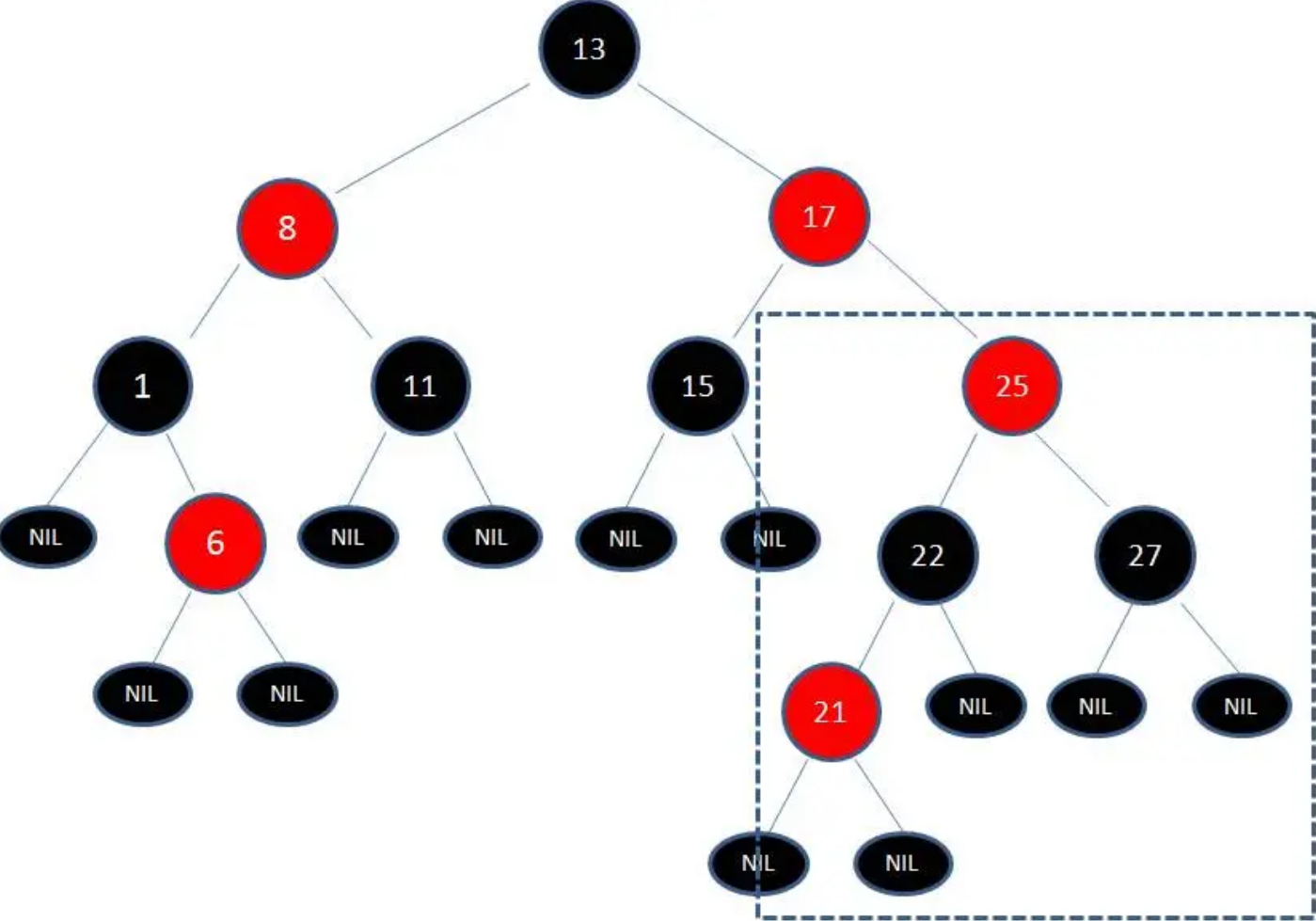
调整第1步:变色
把节点25及其子结点22和27进行变色处理,此时红黑树会出现一个问题:节点17和节点25是连续的两个红色节点,违反了规则3 (每个红色节点的两个子节点都是黑色)。
如果把节点17变成黑色节点,也会出现违反规则4:任何一个结点向下遍历到叶子结点,所经过的黑结点个数必须相等(相同的黑色高度)
调整第2步:左旋转
当变色已无法解决问题时,就需要通过旋转来解决,把节点13看做X,把节点17看做Y,进行左旋转。
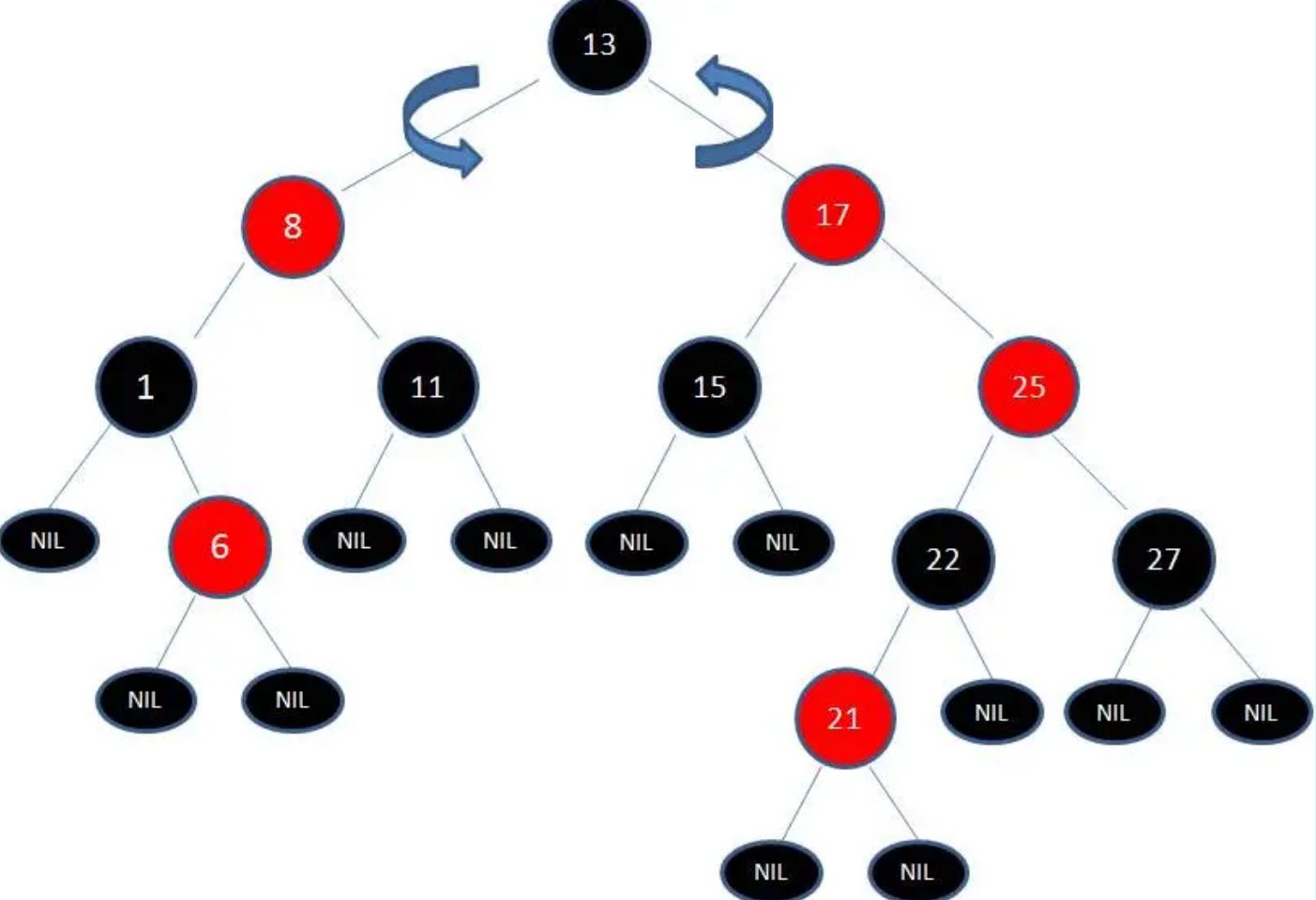
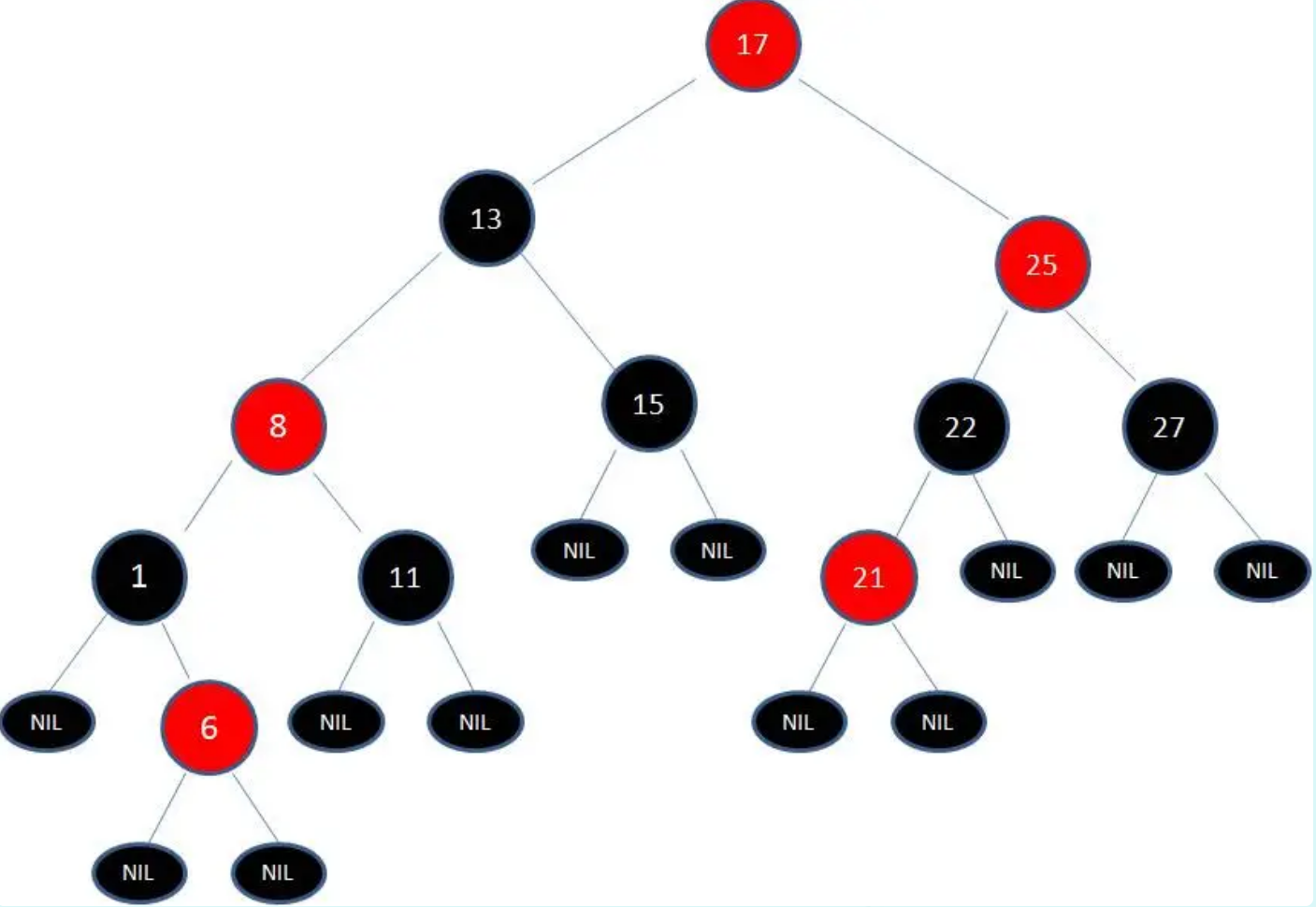
调整第3步:变色
由于根节点必须是黑色节点,所以需要变色。
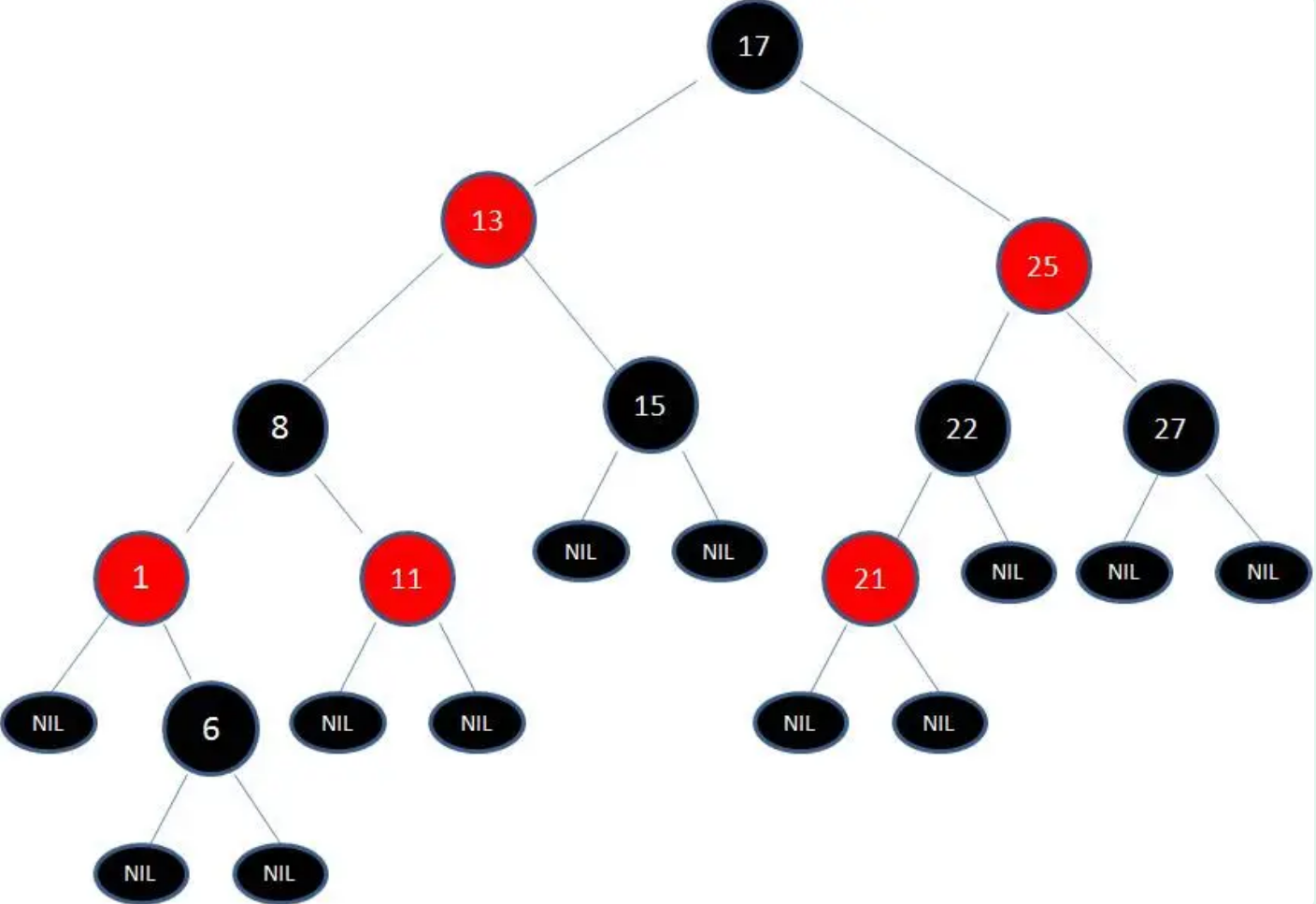
调整第4步:右旋转
由于红黑树中路径(17 -> 8 -> 6 -> NIL)的黑色节点个数是4,其他路径的黑色节点个数是3,违反规则4:任何一个结点向下遍历到叶子结点,所经过的黑结点个数必须相等。
所以需要把节点13看做X,节点8看做Y,进行右旋转
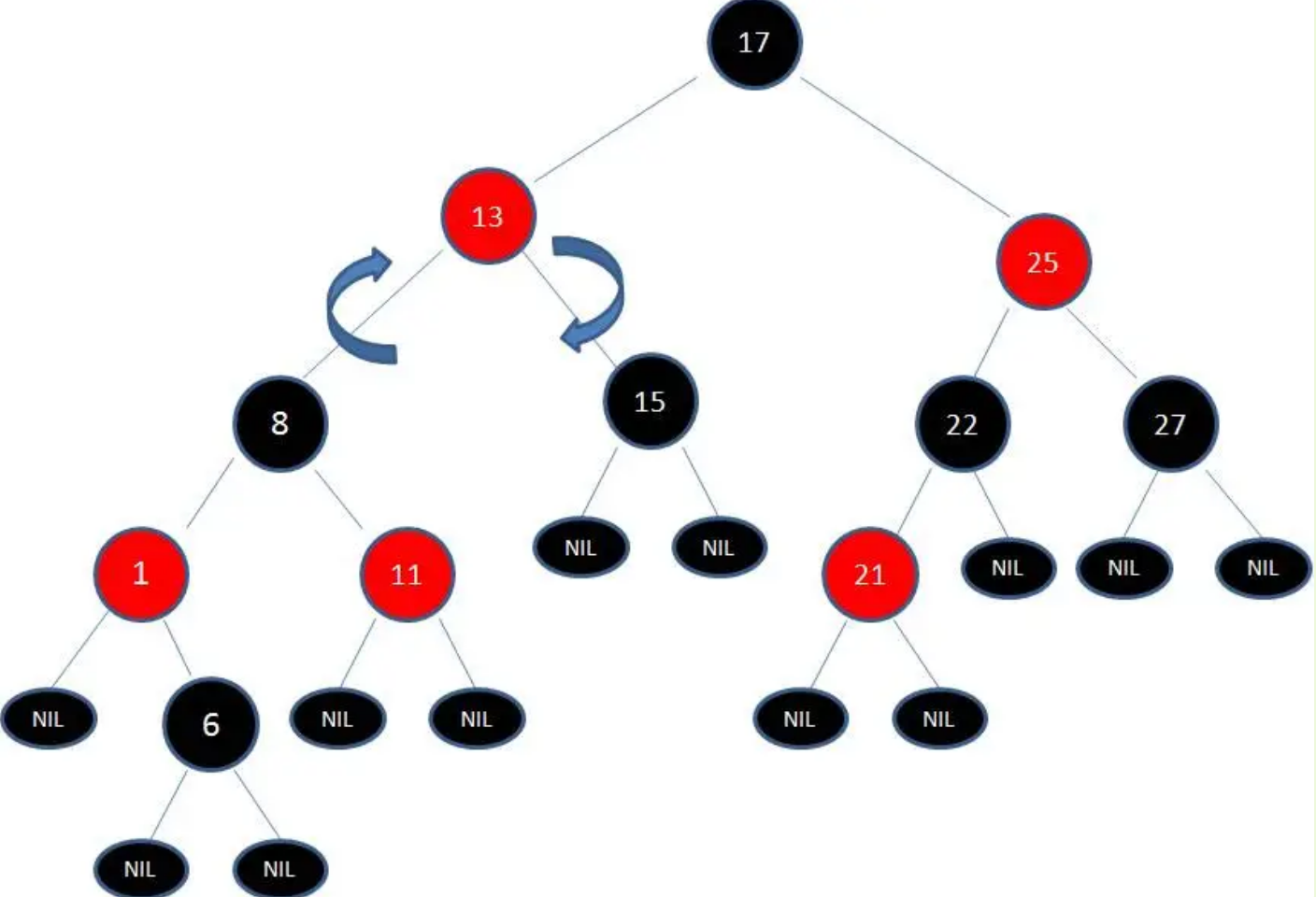
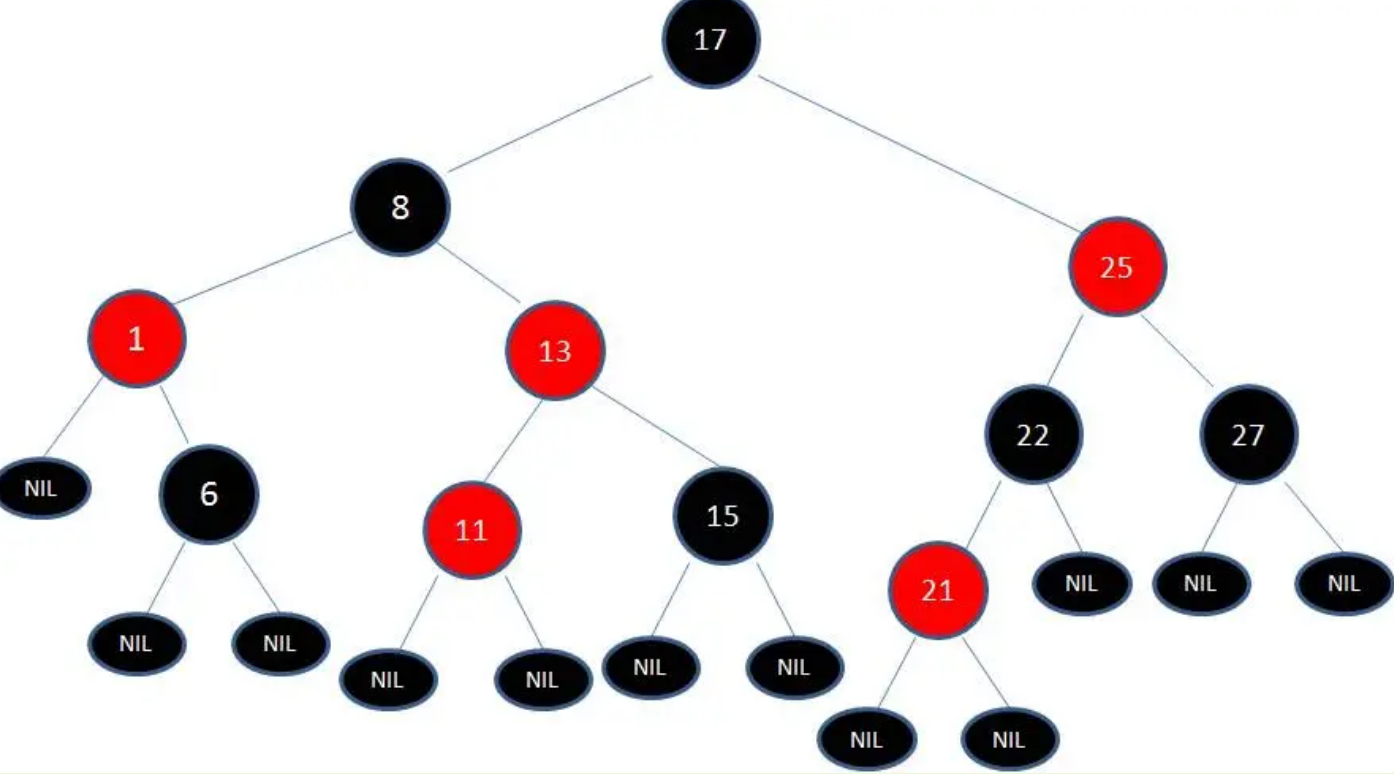
调整第5步:变色
最后根据规则,重新变色。